Purpose
This seminar will show you how to decompose, probe, and plot two-way interactions in linear regression using the margins command in Stata. This page is based off of the seminar Decomposing, Probing, and Plotting Interactions in R.
Outline
Throughout the seminar, we will be covering the following types of interactions:
- Continuous by continuous
- Continuous by categorical
- Categorical by categorical
We can probe or decompose each of these interactions by asking the following research questions:
- What is the predicted Y given a particular X and W? (predicted value)
- What is relationship of X on Y at particular values of W? (simple slopes/effects)
- Is there a difference in the relationship of X on Y for different values of W? (comparing simple slopes)
Proceed through the seminar in order or click on the hyperlinks below to go to a particular section:
- Main vs. Simple effects (slopes)
- Predicted Values vs. Slopes
- Continuous by Continuous
- Be wary of extrapolation
- Simple slopes for a continuous by continuous model
- Plotting a continuous by continuous interaction
- Testing simple slopes in a continuous by continuous model
- Testing differences in predicted values at a particular level of the moderator
- (Optional) Manually calculating the simple slopes
- Continuous by Categorical
- Categorical by Categorical
This seminar page was inspired by Analyzing and Visualizing Interactions in SAS and parallels Decomposing, Probing, and Plotting Interactions in R.
Requirements
Before beginning the seminar, please make sure you have Stata installed. The dataset used in the seminar can be found here as a Stata file exercise.dta or as a CSV file exercise.csv. You can also import the data directly into Stata via the URL using the following code:
use https://stats.idre.ucla.edu/wp-content/uploads/2020/06/exercise, clear
Before you begin the seminar, load the data as above and create value labels forgender and prog (exercise type):
label define progl 1 "jog" 2 "swim" 3 "read" label define genderl 1 "male" 2 "female" label values prog progl label values gender genderl
Download links
- PowerPoint slides: interactions_stata.pptx
- PowerPoint slides as a PDF: interactions_stata.pdf
- Complete Stata code: interactions.do
- Part 2 + Lab PowerPoint slides: interactions_stata_lab.pptx
- Part 2 + Lab PowerPoint slides as a PDF: interactions_stata_lab.pdf
- (Bonus) Three-way interactions PowerPoint slides: three-way interactions.pptx
- (Bonus) Three-way interactions Stata Do File: threeway-interactions.do
Motivation
Suppose you are doing a simple study on weight loss and notice that people who spend more time exercising lose more weight. Upon further analysis you notice that those who spend the same amount of time exercising lose more weight if they are more effortful. The more effort people put into their workouts, the less time they need to spend exercising. This is popular in workouts like high intensity interval training (HIIT).
You know that hours spent exercising improves weight loss, but how does it interact with effort? Here are three questions you can ask based on hypothetical scenarios.
- I’m just starting out and don’t want to put in too much effort. How many hours per week of exercise do I need to put in to lose 5 pounds?
- I’m moderately fit and can put in an average level of effort into my workout. For every one hour increase per week in exercise, how much additional weight loss do I expect?
- I’m a crossfit athlete and can perform with the utmost intensity. How much more weight loss would I expect for every one hour increase in exercise compared to the average amount of effort most people put in?
Additionally, we can visualize the interaction to help us understand these relationships.
Weight Loss Study
This is a hypothetical study of weight loss for 900 participants in a year-long study of 3 different exercise programs, a jogging program, a swimming program, and a reading program which serves as a control activity. Variables include
loss: weight loss (continuous), positive = weight loss, negative scores = weight gain
hours: hours spent exercising (continuous)
effort: effort during exercise (continuous), 0 = minimal physical effort and 50 = maximum effort
prog: exercise program (categorical)
- jogging=1
- swimming=2
- reading=3
gender: participant gender (binary)
- male=1
- female=2
Definitions
What exactly do I mean by decomposing, probing, and plotting an interaction?
- decompose: to break down the interaction into its lower order components (i.e., predicted means or simple slopes)
- probe: to use hypothesis testing to assess the statistical significance of simple slopes and simple slope differences (i.e., interactions)
- plot: to visually display the interaction in the form of simple slopes such as values of the dependent variable are on the y-axis, values of the predictor is on the x-axis, and the moderator separates the lines or bar graphs
Let’s define the essential elements of the interaction in a regression:
- DV: dependent variable (Y), the outcome of your study (e.g., weight loss)
- IV: independent variable (X), the predictor of your outcome (e.g., time exercising)
- MV: moderating variable (W) or moderator, a predictor that changes the relationship of the IV on the DV (e.g, effort)
- coefficient: estimate of the direction and magnitude of the relationship between an IV and DV
- continuous variable: a variable that can be measured on a continuous scale, e.g., weight, height
- categorical or binary variable: a variable that takes on discrete values, binary variables take on exactly two values, categorical variables can take on 3 or more values (e.g., gender, ethnicity)
- main effects or slopes: effects or slopes for models that do not involve interaction terms
- simple slope: when a continuous IV interacts with an MV, its slope at a particular level of an MV
- simple effect: when a categorical IV interacts with an MV, its effect at a particular level of an MV
Main vs. Simple effects (slopes)
Let’s do a brief review of multiple regression. Suppose you have an outcome $Y$, and two continuous independent variables $X$ and $W$.
$$\hat{Y}= \hat{b}_0 + \hat{b}_1 X + \hat{b}_2 W$$
We can interpret the coefficients as follows:
- $\hat{b}_0$: the intercept, or the predicted outcome when $X=0$ and $W=0$.
- $\hat{b}_1$: the slope (or main effect) of $X$; for a one unit change in $X$ the predicted change in $Y$
- $\hat{b}_2$: the slope (or main effect) of $W$; for a one unit change in $W$ the predicted change in $Y$
Here only the intercept is interpreted at zero values of the IV’s. For a more thorough explanation of multiple regression look at Section 1.5 of the seminar Introduction to Regression with SPSS.
Interactions are formed by the product of any two variables.
$$\hat{Y}= \hat{b}_0 + \hat{b}_1 X + \hat{b}_2 W + \hat{b}_3 XW$$
Each coefficient is interpreted as:
- $\hat{b}_0$: the intercept, or the predicted outcome when $X=0$ and $W=0$.
- $\hat{b}_1$: the simple effect or slope of $X$, for a one unit change in $X$ the predicted change in $Y$ at $W=0$
- $\hat{b}_2$: the simple effect or slope of $W$, for a one unit change in $W$ the predicted change in $Y$ at $X=0$
- $\hat{b}_3$: the interaction of $X$ and $W$, the change in the slope of $X$ for a one unit increase in $W$ (or vice versa)
For an interaction model, not only is the intercept fixed at 0 of $X$ and $W$, but each coefficient of an IV interacted with an MV is interpreted at zero of the MV. We say that the effect $X$ varies by levels of $W$ (and identically, that the effect $W$ varies by levels of $X$). Focusing on $X$ as our IV and $W$ as our MV, with a rearrangement of the terms in our model,
$$\hat{Y}= \hat{b}_0 + \hat{b}_2 W + (\hat{b}_1+\hat{b}_3 W)X$$
we can see that the coefficient for $X$ is now $\hat{b}_1+\hat{b}_3 W$, which means the coefficient of $X$ is a function of $W$. For example, if $W=0$ then the slope of $X$ is $\hat{b}_1$; but if $W=1$, the slope of $X$ is $\hat{b}_1+\hat{b}_3$. The coefficient $\hat{b}_3$ is thus the additional increase in the effect or slope of $X$ as $W$ increases by one unit.
Predicted Values vs. Slopes
After fitting a regression model, we are often interested in the predicted mean given a fixed value of the IV’s or MV’s. For example, suppose we want to know the predicted weight loss after putting in two hours of exercise. We fit the main effects model,
$$\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1*\mbox{Hours}.$$
Using the command regress, we specify the following syntax where the dependent variable comes before the independent variables:
regress loss hours
and obtain the following (shortened output):
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hours | 2.469591 .9478805 2.61 0.009 .6092722 4.32991
_cons | 5.07572 1.955005 2.60 0.010 1.238809 8.912632
------------------------------------------------------------------------------
We can use the coefficients obtained from the table to specify the equation form and get:
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47*\mbox{Hours}.$$
We can plug in $\mbox{Hours}=2$ to get
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47 (2) = 10.02.$$
The predicted weight loss is 10.02 pounds from 2 hours of exercise (remember, this is a hypothetical study). This is an example that we can work by hand, but we can also ask margins to help us.
The margins command (introduced in Stata 11) is a post-estimation command to obtain marginal means, predicted values and simple slopes. Post-estimation means that you must run a type of linear model before running margins by first running the regress command. In our example, we are requesting predicted values using the at option. In Stata, command options follow after a comma.
margins, at(hours=2)
Expression : Linear prediction, predict()
at : hours = 2
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 10.0149 .4685077 21.38 0.000 9.095405 10.9344
------------------------------------------------------------------------------
We get a predicted value of 10.01, which matches our computed value of 10.02 (rounded to the single digit). Losing 10 pounds of weight for 2 hours of exercise seems a little unrealistic. Maybe this study was conducted on the moon.
Understanding slopes in regression
Now that we understand predicted values how do you obtain a slope? Well a slope is defined as
$$ b = \frac{\mbox{change in } Y }{\mbox{change in } X } =\frac{\Delta Y }{\Delta X } $$
where $\Delta Y = y_2 – y_1$ and $\Delta X = x_2 – x_1 $. In regression, we usually talk about a one-unit change in $X$ so that $\Delta X = 1 – 0 = 1 $. This makes our slope formula simply $$ b = \Delta Y.$$ So how do we find our slope? Going back to our original equation,
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47 * \mbox{Hours}. $$
We can interpret the $\hat{b}_1 = 2.47$ as a slope, as $\hat{b}_1$ is interpreted as the change in $Y$ for a one unit change in $X$. In our case, for a one hour increase in time put in, we achieve 2.47 pounds of weight loss. In fact, we can derive the slope by obtaining two predicted values, one for Hours =0 and another for Hours =1. The symbol “|” means given, which means holding a variable at a particular value. Plugging in $X=0$ into our original regression equation,
$$\hat{\mbox{WeightLoss}} | _{\mbox{Hours}= 0} = 5.08 + 2.47 (0) = 5.08.$$ Similarly, we can predict weight loss for Hours = 1 $$\hat{\mbox{WeightLoss}} | _{\mbox{Hours} = 1} = 5.08 + 2.47 (1) = 7.55.$$
Now we have $y_2 = 7.55$ and $y_1 =5.08$, using our slope formula $b = 7.55 -5.08 = 2.47$. We obtain 2.47, which equals our value of $\hat{b}_1.$ This means that $\hat{b}_1$ is in fact the slope of Hours, given a one hour change. Of course we can easily obtain the slope using from the regress output, but for edification purposes, let’s see how we can obtain this using margins. However, instead of using the at option, we use the option dydx which stands for the partial derivative. Without going into calculus, you can think of the partial derivative in this case as the slope of hours.
margins, dydx(hours)
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hours | 2.469591 .9478805 2.61 0.009 .6092722 4.32991
------------------------------------------------------------------------------
We are telling margins to calculate the partial derivative or the slope for the variable Hours. Since this is a main effect (or slope), the slope does not vary as we vary the value of hours. In the Continuous by Continuous section, we will see how the slope can change in the presence of an interaction.
Quiz: (True or False) In the margins command, the option dydx is used to estimate predicted values and at is used to estimate simple slopes.
Answer: False, the option dydx estimates simple slopes.
Exercise
Predict two values of weight loss for Hours = 10 and Hours = 20 using at, then calculate the slope by hand. How do the results compare with dydx?
Plotting a regression slope
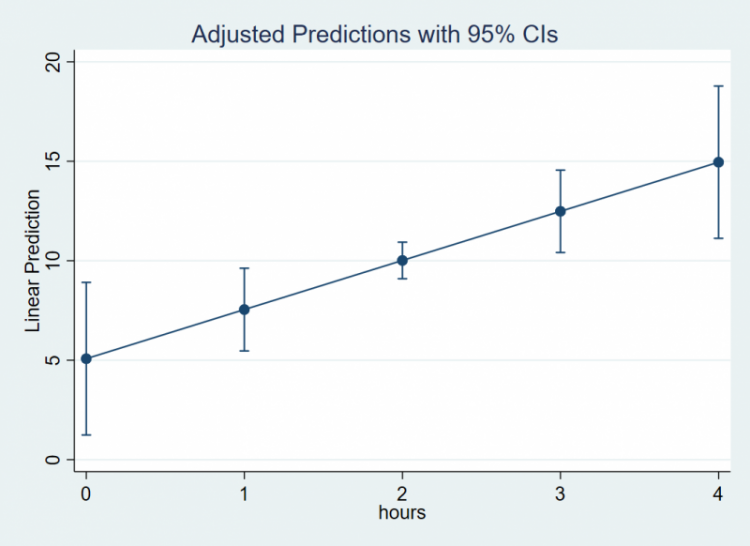
Visualizing is always a good thing. Let’s suppose we want to create a plot of the relationship of Hours and Weight Loss. The command marginsplot allows us to easily plot this. Note that marginsplot must always follow margins . First, decide a range of values of Hours so that we have enough points on the x-axis to create a line. Recall that to obtain predicted values of Weight Loss at specific Hours we need the at option. Here the code at(hours=(0(1)4)) tells Stata that we want the minimum to be 0 and the maximum to be 4, the 1 in the parenthesis means increment by 1. This is equivalent to specifying at(hours=(0 1 2 3 4)). Follow this code by marginsplot to generate the graph; Stata automatically knows to put Hours on the x-axis and Weight Loss on the y-axis
margins, at(hours=(0(1)4)) marginsplot
The plot look like the following, and can be interpreted as for every one unit increase in Hours, there is a 2.47 increase in Weight Loss.
In the next section we will discuss how to estimate and interpret slopes that vary with levels of another variable (i.e., a simple slope).
Continuous by Continuous
We know that amount of exercise is positively related with weight loss. Given the recent news about the efficacy of high intensity interval training (HIIT), perhaps we can achieve the same weight loss goals in a shorter time interval if we increase our exercise intensity. The question we ask is does effort (W) moderate the relationship of Hours (X) on Weight Loss (Y)? The model to address the research question is
$$\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1 \mbox{Hours} + \hat{b}_2 \mbox{Effort} + \hat{b}_3 \mbox{Hours*Effort}.$$
We can fit this in Stata with the following code:
regress loss c.hours##c.effort
Two things to note. First, when you specify an interaction in Stata, it’s preferable to also specify whether the predictor is continuous or categorical (by default Stata assumes interaction variables are categorical). A c. precedes a continuous variable and an i. precedes a categorical one. Here we have two continuous variables, so we specify c.hours and c.effort. Second, the ## between the two variables specifies a two way interaction and is equivalent to adding the lower order terms to the interaction term specified by a single #
regress loss hours effort c.hours#c.effort
You then obtain the following shortened output:
----------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------------+----------------------------------------------------------------
hours | -9.375681 5.663921 -1.66 0.098 -20.49178 1.740415
effort | -.0802763 .3846469 -0.21 0.835 -.8351902 .6746375
|
c.hours#c.effort | .3933468 .1875044 2.10 0.036 .0253478 .7613458
|
_cons | 7.798637 11.60362 0.67 0.502 -14.97479 30.57207
----------------------------------------------------------------------------------
The interaction Hours*Effort is significant, which suggests that the relationship of Hours on Weight loss varies by levels of Effort. Before decomposing the interaction let’s interpret each of the coefficients.
- $\hat{b}_0$
_cons: the intercept, or the predicted outcome when Hours = 0 and Effort = 0. - $\hat{b}_1$
hours: the simple slope of Hours, for a one unit change in Hours, the predicted change in weight loss at Effort=0. - $\hat{b}_2$
effort: the simple slope of Effort, for a one unit change in Effort the predicted change in weight loss at Hours=0. - $\hat{b}_3$
c.hours#c.effort: the interaction of Hours and Effort, the change in the slope of Hours for every one unit increase in Effort (or vice versa).
Before proceeding, let’s discuss our findings for $\hat{b}_1$. Although we may think that the slope of Hours should be positive at levels of Effort, remember that in this case, Effort is zero. As we see in our data, this is improbable as the minimum value of effort is 12.95.
summarize effort
Variable | Obs Mean Std. Dev. Min Max
-------------+---------------------------------------------------------
effort | 900 29.65922 5.142764 12.949 44.07604
Be wary of extrapolation
Suppose we want to find the predicted weight loss given two hours of exercise and an effort of 30. As before, use the at option after margins to specify 2 for Hours and 30 for Effort:
margins, at(hours=2 effort=30)
The output we obtain is:
Expression : Linear prediction, predict()
at : hours = 2
effort = 30
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 10.23979 .4530791 22.60 0.000 9.350572 11.12901
------------------------------------------------------------------------------
The results show that predicted weight loss is 10.2 pounds if we put in two hours of exercise and an effort level of 30; this seems reasonable. Let’s see what happens when we predict weight loss for two hours of exercise given an effort level of 0.
margins, at(hours=2 effort=0)
Expression : Linear prediction, predict()
at : hours = 2
effort = 0
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | -10.95273 2.647602 -4.14 0.000 -16.14895 -5.756502
------------------------------------------------------------------------------
The predicted weight gain at Effort=0 and Hours=2 is now 11 pounds. It is unreasonable to assume that a person who exercises for 2 hours will first of all exert no effort and second of all gain weight! This is demonstration of the fact that we are extrapolating, which means we are making predictions about our data beyond what the data can support. This is why we should always choose reasonable values of our predictors in order to interpret our data properly.
In order to achieve plausible values, some researchers may choose to do what is known as centering, which is subtracting a constant $c$ from the variable so that $X^{*} = X-c$. Since $X^{*} = 0$ implies $X=c$, the intercept, simple slopes and simple effects are interpreted at $X=c$. A popular constant is $c=\bar{x}$, so that all intercepts, simple slopes and simple effects are interpreted at the mean of $X$. Extrapolation then becomes a non-issue.
Simple slopes for a continuous by continuous model
We know to choose reasonable values when predicting values. The same concept applies when decomposing an interaction. Our output suggests that Hours varies by levels of Effort. Since effort is continuous, we can choose an infinite set of values with which to fix effort. For ease of presentation, some researchers pick three representative values of Effort with which to estimate the slope of Hours. This is often known as spotlight analysis, which was made popular by Leona Aiken and Stephen West’s book Multiple Regression: Testing and Interpreting Interactions (1991). Traditional spotlight analysis was made for a continuous by categorical variable but we will borrow the same concept here. What three values should we choose? Aiken and West recommend plotting three lines for Hours, one at the mean level of Effort, a second at one standard deviation about the mean level of Effort, and finally a third at one standard deviation below the mean level of effort. In symbols, we have
$$ \begin{eqnarray} \mbox{EffA} & = & \overline{\mbox{Effort}} + \sigma({\mbox{Effort}}) \\ \mbox{Eff} & = & \overline{\mbox{Effort}} \\ \mbox{EffB} & = & \overline{\mbox{Effort}} – \sigma({\mbox{Effort}}). \end{eqnarray} $$
In Stata, we can use summarize to store the mean and standard deviation of effort into a list. The command return then invokes invoke the objects in the list,
summarize effort
return list
scalars:
r(N) = 900
r(sum_w) = 900
r(mean) = 29.65921892801921
r(Var) = 26.44801661342404
r(sd) = 5.142763519103716
r(min) = 12.94899940490723
r(max) = 44.07604217529297
r(sum) = 26693.29703521729
The object r(mean) gives us the mean and r(sd) gives us the standard deviation. We can then store these values into what is known as a global variable, which allows the user to recall the value of that variable for future use. In the commands below, we create three global variables effa, eff, effb which corresponds to “high”, “medium” and “low” values of effort. For ease of presentation in the plot we will create later, the function round(x,0.1) rounds the value we obtain to the tenths digit
global effa = round(r(mean) + r(sd),0.1) global eff = round(r(mean),0.1) global effb = round(r(mean) - r(sd),0.1)
The mean of effort is about 30. A quick way to check the values of one standard deviation above and one standard deviation below is to make sure that the former (34.8) is higher than the latter (24.5). The command display allows us to view the values of the newly created global variables.
display $effa 34.8 display $effb 24.5
Recall that our simple slope is the relationship of hours on weight loss fixed a particular values of effort. In Stata, we can obtain simple slopes using the margins option dydx. First, we need to specify three values of effort we found above in preparation for spotlight analysis using the at option.
margins, dydx(hours) at(effort=($effa $eff $effb))
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
1._at : effort = 34.8
2._at : effort = 29.7
3._at : effort = 24.5
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hours |
_at |
1 | 4.312787 1.308387 3.30 0.001 1.744927 6.880646
2 | 2.306719 .9148823 2.52 0.012 .511157 4.102281
3 | .2613151 1.352052 0.19 0.847 -2.392243 2.914874
------------------------------------------------------------------------------
The margins command is a post-estimation command that follows regress loss c.hours##c.effort
. Note that our global and return commands do not interfere with regress because only the latter is an estimation command. The dydx(hours) option means that we want the simple slope of hours and the at option specifies that we want these simple slopes at three values of effort, “low”, “medium” and “high” (here it’s 24.5, 29.7 and 34.8).
Looking at the output, we get three separate (simple) slopes for hours. As we increase levels of Effort, the relationship of hours on weight loss seems to increase. Looking at the t-test, the p-values indicate that the simple slope of hours at “high” and “medium” are significant but not at “low”. We can confirm this with [95% Conf. Interval] to see if the 95% confidence interval contains zero. If it the interval contains zero, then the simple slope is not significant. Here it seems that the simple slope of Hours is significant only for mean Effort levels and above. Although not shown in the ouput, in case the user is curious you can calculate the degrees of freedom which is 896 because we have a sample size of 900, 3 predictors and 1 intercept, $df= n-p-1 = 900-3-1=896.$ Now that we understand the output, let’s see what these three simple slopes look like visually.
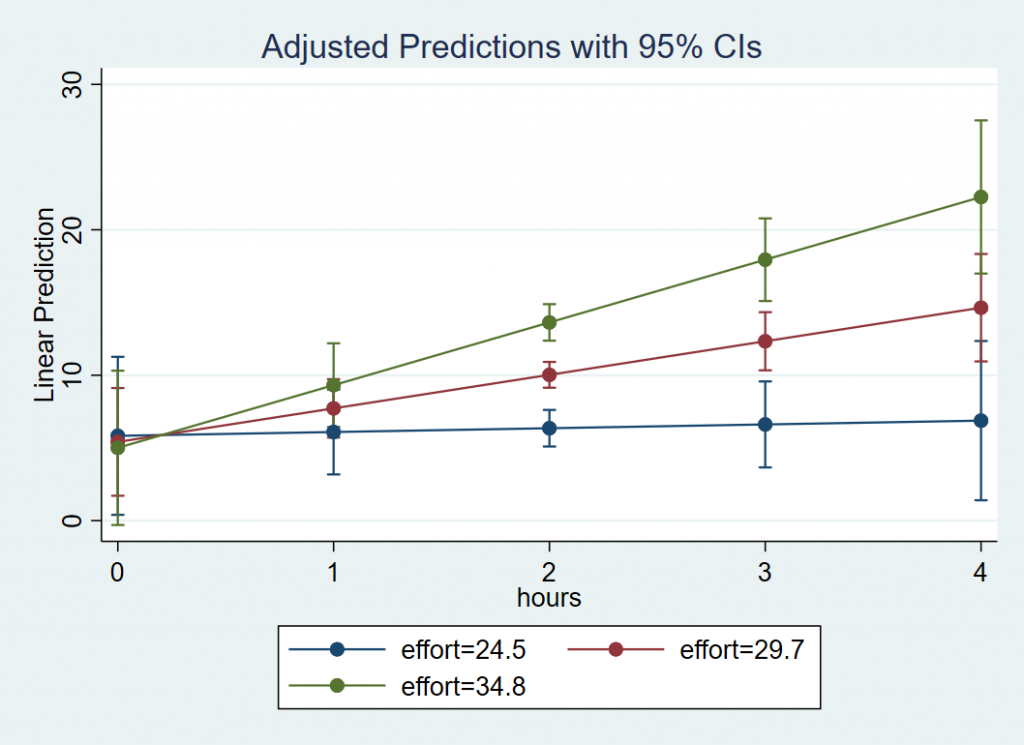
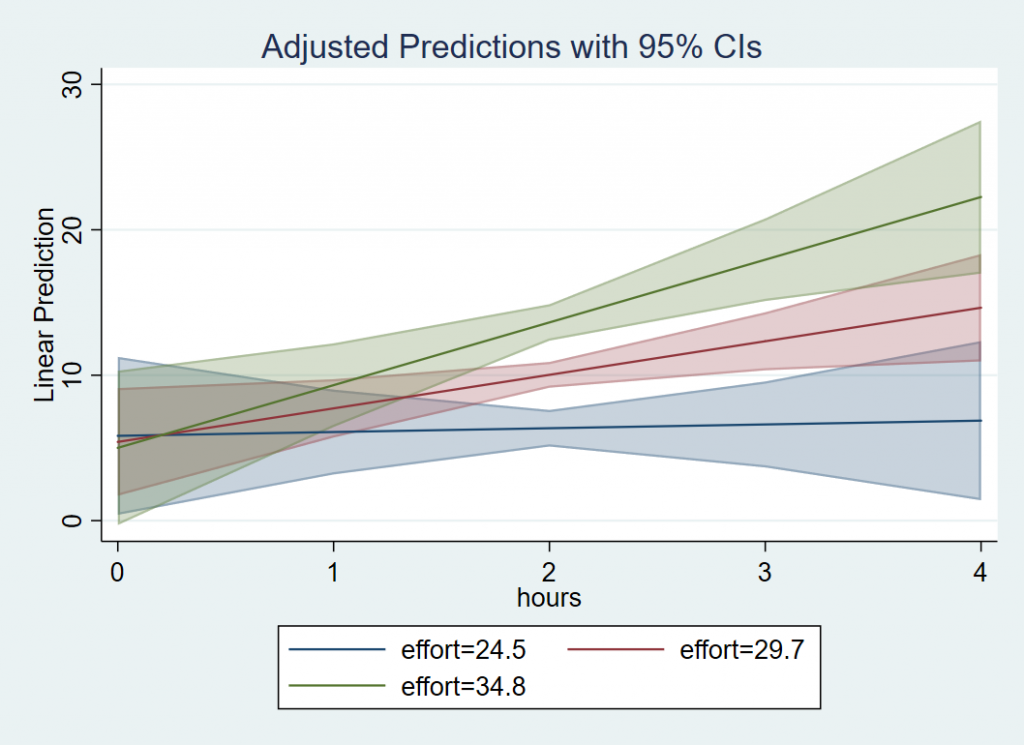
Plotting a continuous by continuous interaction
In order to plot our interaction, we want the IV (Hours) to be on the x-axis and the MV (Effort) to separate the lines. For the x-axis, we need to create a sequence of values to span a reasonable range of Hours, but we need only three values of Effort for spotlight analysis. First, use that at option to create a sequence of Hours values from 0 to 4, incremented by 1 and Effort is assigned one standard deviation below the mean, at the mean and one standard deviation above the mean. The code and output is listed below. We advise checking the margins output to confirm whether you specified the list correctly. Then we can follow margins with marginsplot. Stata knows to plot Hours on the x-axis and separate lines by Effort because of the order by which we specified the at option. If we had used at(effort=($effa $eff $effb) hours=(0(1)4)), then Effort would have been on the x-axis separated by Hours.
margins, at(hours=(0(1)4) effort=($effa $eff $effb)) marginsplot
Quiz: T/F The command margins, at(hours=(0(1)4) effort=($effa $eff $effb)) tells Stata to plot Hours as the independent variable and Effort as the moderator.
Answer: True
Here is the plot we obtain:
Just as we observed from margins, dydx(hours) at(effort=($effa $eff $effb)), the simple slope of Hours at “low” effort is flat, but is positive for “medium” effort and above. The results suggest that hours spent exercising is only effective for weight loss if we put in more effort, which supports the rationale for high intensity interval training. At the highest levels of Effort, we achieve higher weight loss for a given time input.
(Optional) Obtaining confidence interval bands
In case you prefer confidence bands over confidence bars, you can modify the marginsplot code using the option recast. The option and sub-option recast(line) draws the predicted regression line but removes the points associated with each value on the x-axis. This allows us to draw a continuous line which will look more aesthetically pleasing when we overlay the confidence band. The option and sub-option recastci(rarea) “recasts” the confidence interval (ci) bars into confidence ribbons, and finally ciopt(color(%30)) specifies that we want to add transparency to the ribbons. The lower the %##, the more transparent the ribbon will be. Note that transparency is available to Stata 15 or higher.
margins, at(hours=(0(1)4) effort=($effa $eff $effb)) marginsplot, recast(line) recastci(rarea) ciopt(color(%30))
These commands result in the following plot:
 Go to top of page
Go to top of page
Testing simple slopes in a continuous by continuous model
Looking at the graph, we may think that only the slope of “low” effort is significantly different from the others. Let’s confirm if this is true with the following syntax:
margins, dydx(hours) at(effort=($effa $eff $effb)) pwcompare(effects)
First recall that dydx(hours) requests the simple slopes of hours and at(effort=($effa $eff $effb)) requests these simple slopes at Low, Mean and High values of Effort. The new option pwcompare requests pairwise differences of the simple slopes of Hours for each level of effort. Finally (effects) is a suboption pwcompare that requests the unadjusted p-values as well as the 95% confidence intervals for each simple slope comparison.
The output we obtain is as follows:
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
1._at : effort = 34.8
2._at : effort = 29.7
3._at : effort = 24.5
------------------------------------------------------------------------------
| Contrast Delta-method Unadjusted Unadjusted
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hours |
_at |
2 vs 1 | -2.006068 .9562721 -2.10 0.036 -3.882862 -.1292739
3 vs 1 | -4.051472 1.931295 -2.10 0.036 -7.841861 -.2610826
3 vs 2 | -2.045404 .975023 -2.10 0.036 -3.958999 -.1318087
------------------------------------------------------------------------------
We can see that even though the actual pairwise comparisons differ, the t-statistics and p-values for all three pairwise comparisons are the same. Furthermore, this p-value matches that of the interaction term in regress loss c.hours##c.effort
----------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------------+----------------------------------------------------------------
.... (output omitted) ...
c.hours#c.effort | .3933468 .1875044 2.10 0.036 .0253478 .7613458
----------------------------------------------------------------------------------
This is not a coincidence because for a continuous by continuous interaction, all comparisons of simple slopes result in the same p-value as the interaction itself (we will not go into detail about why, but it has to do with the slope formula from above and the fact that we divide the change in Y by a proportional change in X). Back to our intuition that the slopes for the “low” effort group is lower than that of “medium” or “high” group. Based on the tests above, yes the maginitue of the slope is larger between “low” and “high” versus “medium” and “high”, but the two p-values are the same.
Testing differences in predicted values at a particular level of the moderator
Although the p-values of the difference in the Hours slopes are identical across levels of the effort in a continuous by continuous interaction, it may be that the predicted value of hours differs by levels of Effort. From the plot, we may assume that for a person who has exercised for four hours, there is a a difference in predicted weight loss at low effort (one SD below) versus high effort (one SD above).
In order to test this, we need to generate a new list where hours=4, and effort is only specified at the low and high levels (look back at the predicted values section). Now we are no longer testing simple slopes but predicted values, so we use the at option and not dydx. First, we check that our list was correctly specified at Hour=4 and Effort at low and high levels.
margins, at(hours=4 effort=($effa $effb))
Looking at 1._at and 2._at, the output corresponds to the predicted Weight Loss at Hours = 4 and Effort = 34.8 and 24.8 respectively. The values we obtain are 22.26 and 6.88.
Expression : Linear prediction, predict()
1._at : hours = 4
effort = 34.8
2._at : hours = 4
effort = 24.5
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 22.25617 2.683877 8.29 0.000 16.98875 27.52359
2 | 6.877127 2.789889 2.47 0.014 1.401648 12.35261
------------------------------------------------------------------------------
Next, we request pairwise differences of these two predicted values at the Hours and Effort specified using the option and sub-option pwcompare(effects) after margins.
margins, at(hours=4 effort=($effa $effb)) pwcompare(effects)
The output we obtain is as follows
... (output omitted) ...
------------------------------------------------------------------------------
| Delta-method Unadjusted Unadjusted
| Contrast Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
2 vs 1 | -15.37904 3.972949 -3.87 0.000 -23.17641 -7.58167
------------------------------------------------------------------------------
From the pairwise contrast we verify that 6.88-22.26 = -15.38, and the p-value indicates that it is significant, verifying our observations from the graph that for 4 hours of exercise, high effort will result in 15 pounds more weight loss than low effort. Note that the Unadjusted p-value and 95% confidence intervals means that these have not been corrected for Type 1 error. Since we only made one comparison, no Type 1 error correction is required.
(Optional) Manually calculating the simple slopes
Recall that for a continuous by continuous interaction model we can re-arrange the equation such that
$$\hat{Y}= \hat{b}_0 + \hat{b}_2 W + (\hat{b}_1+\hat{b}_3 W)X.$$
Rerranging the terms allows you to obtain a new simple slope of $X$ defined as $(\hat{b}_1+\hat{b}_3 W)X$, which means that the slope of $X$ depends on values of $W$. Let’s see how we can derive the simple slope by hand (without calculus).
First, we consider the definition of the simple slope of $X$, which is defined as the slope of $X$ for a fixed value of $W=w$. Recall that the slope (which we call $m$) is the change in $Y$ over the change in $X$,
$$ b = \frac{\mbox{change in } Y }{\mbox{change in } X } =\frac{\Delta Y }{\Delta X }.$$
To simplify our notation, we consider our model before fitting it with the data (to eliminate the hat symbol). Let $\Delta {Y} = Y|_{X=1, W=w} – Y|_{X=0, W=w}$ and $\Delta {X} = X_1 – X_0.$ In regression we consider a one unit change in $X$ so $\Delta {X}=1.$ Then the slope $m$ depends only on the change in $Y$. Since a simple slope depends on levels of $W$, $m_{W=w}$ means we calculate the slope at a fixed constant $w$. Let’s calculate two simple slopes, $m_{W=0}$ and $m_{W=1}$,
$$ \begin{eqnarray} m_{W=1} & = & Y|_{X=1, W=1} – Y|_{X=0, W=1} \\ m_{W=0} & = & Y|_{X=1, W=0} – Y|_{X=0, W=0}. \end{eqnarray} $$
Each $Y$ is a predicted value, for a given $X=x$ and $W=w$. Simply plug in each value into our original interaction model,
$$ \begin{eqnarray} Y|_{X=1, W=1} &=& \hat{b}_0 + \hat{b}_1 (X=1) + \hat{b}_2 (W=1) + \hat{b}_3 (X=1)*(W=1) &=& \hat{b}_0 + \hat{b}_1 + \hat{b}_2 + \hat{b}_3\\ Y|_{X=0, W=1} &=& \hat{b}_0 + \hat{b}_1 (X=0) + \hat{b}_2 (W=1) + \hat{b}_3 (X=0)*(W=1) &=& \hat{b}_0 + \hat{b}_2 \\ Y|_{X=1, W=0} &=& \hat{b}_0 + \hat{b}_1 (X=1) + \hat{b}_2 (W=0) + \hat{b}_3 (X=1)*(W=0) &=& \hat{b}_0 + \hat{b}_1 \\ Y|_{X=0, W=0} &=& \hat{b}_0 + \hat{b}_1 (X=0) + \hat{b}_2 (W=0) + \hat{b}_3 (X=0)*(W=0) &=& \hat{b}_0. \end{eqnarray} $$
Substituting these four equations back into the simple slopes we get:
$$ \begin{eqnarray} m_{W=1} & = & Y|_{X=1, W=1} – Y|_{X=0, W=1} & = & (\hat{b}_0 + \hat{b}_1 + \hat{b}_2 + \hat{b}_3) – (\hat{b}_0 + \hat{b}_2) & = & \hat{b}_1 + \hat{b}_3 \\ m_{W=0} & = & Y|_{X=1, W=0} – Y|_{X=0, W=0} & = & (\hat{b}_0 + \hat{b}_1) – (\hat{b}_0) &=& \hat{b}_1. \end{eqnarray} $$
Now consider our simple slope formula $(\hat{b}_1+\hat{b}_3 W)X$. If we plug in $W=1$ we obtain $\hat{b}_1+\hat{b}_3$ which equals $m_{W=1}$ and if you plug in $W=0$ we obtain $\hat{b}_1$ which equals $m_{W=0}$. Isn’t math beautiful?
Finally, to get the interaction for a continuous by continuous interaction, take the difference in the simple slope of $m_{W=1}$ and $m_{W=0}$ (you can take any one unit change in $W$ to get the same simple slope). Therefore $m_{W=1}-m_{W=0}= (\hat{b}_1 + \hat{b}_3) – (\hat{b}_1) = \hat{b}_3$ which is exactly the same as the interaction coefficient $\hat{b}_3$.
Exercise
The following exercise will guide you through deriving the interaction term using predicted values.
- Obtain predicted values for the following values and store the results into global variables y00, y10, y01,y11
- Hours = 0, Effort = 0 (y00)
- Hours = 1, Effort = 0 (y10)
- Hours = 0, Effort = 1 (y01)
- Hours = 1, Effort = 1 (y11)
The following steps will walk you through the process. We continue to use
marginsexcept that we add the optionpostrecall the results later andcoeflegendrequests the label of the corresponding predicted value.margins, at(hours=(0 1) effort=(0 1)) post coeflegend Expression : Linear prediction, predict() 1._at : hours = 0 effort = 0 2._at : hours = 0 effort = 1 3._at : hours = 1 effort = 0 4._at : hours = 1 effort = 1 ------------------------------------------------------------------------------ | Margin Legend -------------+---------------------------------------------------------------- _at | 1 | 7.798637 _b[1bn._at] 2 | 7.718361 _b[2._at] 3 | -1.577045 _b[3._at] 4 | -1.263974 _b[4._at] ------------------------------------------------------------------------------We can see from the output that the predicted Weight Loss at Effort=0 and Hours=0 is 7.80, assigned the legend label
_b[1bn._at]. Now we are ready to assign each of these four values to corresponding global variablse using the following code.global y00 = _b[1bn._at] global y01 = _b[2._at] global y10 = _b[3._at] global y11 = _b[4._at]
To ensure that we’ve assigned the correct values, use the
displaycommand, with the$prefix indicating that we are referring to a previously assigned global variable in Stata. We can request multiple displays in the same line with a comma separating global variables.display $y00, $y01, $y10, $y11 7.7986369 7.7183605 -1.5770445 -1.2639741
You can also manually calculate the predicted values to aid understanding using the following equations.
\begin{eqnarray} y_{00} &=& 7.80 + (-9.38) \mbox{(Hours=0)} + (-0.08) \mbox{(Effort=0)} + (0.393) \mbox{(Hours=0)*(Effort=0)} \\ y_{10} &=& 7.80 + (-9.38) \mbox{(Hours=1)} + (-0.08) \mbox{(Effort=0)} + (0.393) \mbox{(Hours=1)*(Effort=0)} \\ y_{01} &=& 7.80 + (-9.38) \mbox{(Hours=0)} + (-0.08) \mbox{(Effort=1)} + (0.393) \mbox{(Hours=0)*(Effort=1)} \\ y_{11} &=& 7.80 + (-9.38) \mbox{(Hours=1)} + (-0.08) \mbox{(Effort=1)} + (0.393) \mbox{(Hours=1)*(Effort=1)} \end{eqnarray}
- Take the following differences. What coefficients do these difference correspond to in
regress loss c.effort##c.hours? (Hint: one of the differences is a sum of two coefficients)- y10 – y00
- y11 – y01
- Take the difference of the two differences in Step 2. Which coefficient does this correspond to in
regress loss c.effort##c.hours?
Answers: 1) y00 = 7.80, y10 = -1.58, y01 = 7.72, y11 = -1.26; 2) y10 – y00 is $\hat{b}_1=-9.38$, the simple slope of Hours at Effort = 0; y11 – y01 is $\hat{b}_1+\hat{b}_3 = -8.98$, the simple slope of Hours at Effort = 1; 3) $\hat{b}_3=0.394$ is the interaction.
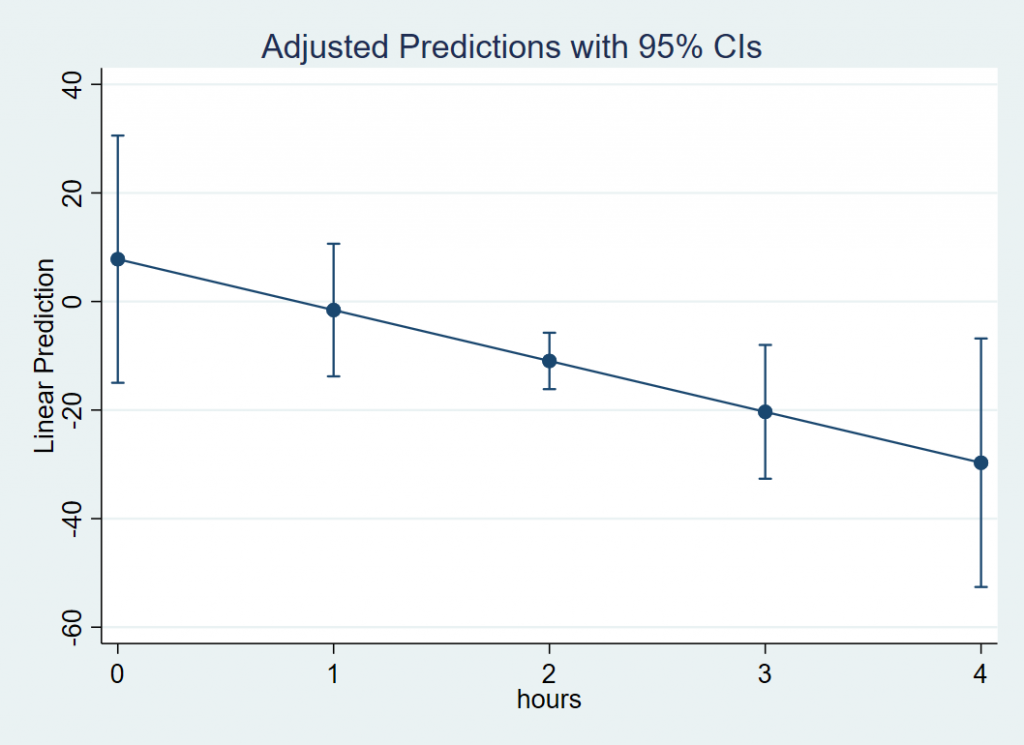
Exercise
Create a plot of hours on the x-axis with effort = 0 using marginsplot. The figure should look like the one below. Do the results seem plausible?
Continuous by Categorical
We know that exercise time positively relates to weight loss from prior studies but suppose we suspect gender differences in this relationship. The research question here is, do men and women (W) differ in the relationship between Hours (X) and Weight loss? This can be modeled by a continuous by categorical interaction where Gender is the moderator (MV) and Hours is the independent variable (IV). Before talking about the model, we have to introduce a new concept called dummy coding which is the default method of representing categorical variables in a regression model.
Suppose we only have two genders in our study, male and female. Dummy coding can be defined as
$$ D = \left\{ \begin{array}{ll} 1 & \mbox{if } X = x \\ 0 & \mbox{if } X \ne x \end{array} \right. $$
Let’s take the example of our variable gender, which can be represented by two dummy codes. The first dummy code $D_{female} = 1$ if $X= \mbox{Female}$, and $D_{female} = 0$ if $X= \mbox{Male}$. The second dummy code $D_{male}= 1$ if $X= \mbox{Male}$ and $D_{male}= 0$ if $X = \mbox{Female}$. The $k=2$ categories of Gender are represented by two dummy variables. However, only $k-1$ or 1 dummy code is needed to uniquely identify gender.
To see why only one dummy code is needed for a binary variable, suppose you have a female participant. Then for that particular participant, $D_{female} = 1$ which means we automatically know that she is not male, so $D_{male}=0$ (of course in the real world gender can be non-binary). If we entered both dummy variables into our regression, it would result in what is known as perfect collinearity (or redundancy) in our estimates and most statistical software programs would simply drop one of the dummy codes from your model.
Now we are ready to fit our model, recalling that we only enter one of the dummy codes. We have to be careful when choosing which dummy code to omit because the omitted group is also known as the reference group. We arbitrarily choose female to be the reference (or omitted) group which means we include the dummy code for males:
$$\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1 \mbox{Hours} + \hat{b}_2 D_{male}+ \hat{b}_3 \mbox{Hours}*D_{male}$$
Quiz: What would the equation look like if we made males the reference group?
Answer: replace $D_{male}$ with $D_{female}$.
Recall that we assigned value labels to the gender variable in the Requirements section in the beginning of the seminar. This step is recommended for categorical variables, and the tabulate command can help us see whether the labeling was effective.
tab gender
gender | Freq. Percent Cum.
------------+-----------------------------------
male | 450 50.00 50.00
female | 450 50.00 100.00
------------+-----------------------------------
Total | 900 100.00
Here we have two levels of gender, male and female, each with a sample size of 450.
Note that these are value labels we have assigned. What’s more important is the underlying numeric value. In order to see this, you can specify the option nolabel
tab gender, nolabel
gender | Freq. Percent Cum.
------------+-----------------------------------
1 | 450 50.00 50.00
2 | 450 50.00 100.00
------------+-----------------------------------
Total | 900 100.00
Here we see that Male is coded 1 and Female is coded 2. The underlying numerical value is important for understanding how Stata handles dummy codes because Stata takes the lowest value and assigns it to the reference group for any linear model command like regress. This means that if we use the prefix i. for gender, Stata specifies Male to be the omitted or reference group. Internally, Stata recodes gender such that Male=0 and Female=1. Let’s confirm whether this is true:
regress i.gender
The (shortened) output we obtain is:
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender |
female | -.1841939 .940519 -0.20 0.845 -2.030065 1.661677
_cons | 10.11293 .6650473 15.21 0.000 8.807707 11.41816
------------------------------------------------------------------------------
The appearance of female under gender means that Stata is including the dummy code for females and omitting the dummy group for males.
Quiz: Write out the equation for the model above.
Answer: $\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1 D_{female}$
Interpreting the coefficients of the continuous by categorical interaction
Now that we understand how Stata handles categorical variables in regress and i. notation, we will go back to our original interaction model. In our original model we entered $D_{male}$ into our model which means we want to omit females. Recall that gender is leveled so that Male=1 and Female=2, which means Males would be the reference group if you use regress loss i.gender. In order to change the reference group so that Females are omitted, we can use ib2.gender which means change the “base” group or reference group in the categorical variable to 2. Internally, Stata is recoding the original variable such that Female=1 and Male=0. The results of the change of base is shown below.
regress loss ib2.gender
... (output omitted) ...
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender |
male | .1841939 .940519 0.20 0.845 -1.661677 2.030065
_cons | 9.928741 .6650473 14.93 0.000 8.623513 11.23397
------------------------------------------------------------------------------
The important difference between the output from regress ib2.genderand the output from regress i.gender is that male appears in the regression output which means Female is now the reference group.T/F Since the original gender variable is coded Male=1 and Female=2, the code regress ib2.gender means that female will appear in the regression output.
Answer: False. The code ib2.gender converts what was 2 in the original variable to become the omitted or reference group; in this case female is omitted and male appears.
Let’s return to the continuous by categorical interaction model where we predict Weight Loss by the Hours (continuous) by Gender (reference group=Female) interaction.
regress loss c.hours##ib2.gender
... (output omitted) ...
--------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
hours | 3.315068 1.331649 2.49 0.013 .7015529 5.928582
|
gender |
male | 3.571061 3.914762 0.91 0.362 -4.11211 11.25423
|
gender#c.hours |
male | -1.723931 1.897895 -0.91 0.364 -5.448768 2.000906
|
_cons | 3.334652 2.73053 1.22 0.222 -2.024328 8.693632
--------------------------------------------------------------------------------
The interaction Hours*Gender is not significant, which suggests that the relationship of Hours on Weight Loss does not vary by Gender. Before moving on, let’s interpret each of the coefficients.
- $\hat{b}_0$
_cons: the intercept, or the predicted weight loss when Hours = 0 in the reference group of Gender, which is $D_{male}=0$ or females. - $\hat{b}_1$
hours: the simple slope of Hours for the reference group $D_{male}=0$ or females. - $\hat{b}_2$
male: the simple effect of Gender or the difference in weight loss between males and females at Hours = 0. - $\hat{b}_3$
gender#c.hours: the interaction of Hours and Gender, the difference in the simple slopes of Hours for males versus females.
The most difficult term to interpret is $\hat{b}_3$. Another way to think about it is if we know the slope of Hours for females, this is the additional slope for males. Since the Hours slope of females is $\hat{b}_1$, the Hours slope of males is $\hat{b}_1 + \hat{b}_3$. The interaction is not significant, but we decide to probe the interaction anyway for demonstration purposes.
Obtaining simple slopes by each level of the categorical moderator
Since our goal is to obtain simple slopes of Hours by gender we use the dydx(hours) option after margins. Since gender is a categorical variable, we specify it before the comma. Remember that continuous variables come after the comma (usually specified at particular values with the at option) and categorical variables usually come before the comma.
margins gender, dydx(hours)
An equivalent and alternative syntax is to specify over as an option after the comma. Conceptually this may make more sense because we are obtaining the simple slopes of Hours over values of Gender. The output is equivalent to the previous command.
margins, dydx(hours) over(gender)
The output we obtain is:
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hours |
gender |
male | 1.591136 1.3523 1.18 0.240 -1.062908 4.245181
female | 3.315068 1.331649 2.49 0.013 .7015529 5.928582
------------------------------------------------------------------------------
The simple slope for females is 3.32, which is exactly the same as $\hat{b}_1$ and males is 1.59 which is $\hat{b}_1 + \hat{b}_3 = 3.32 + (-1.72)$. The 95% confidence interval does not contain zero for females but contains zero for males, so the simple slope is significant for females but not for males.
A common misconception is that since the simple slope of Hours is significant for females but not males, we should have seen a significant interaction. However, the interaction tests the difference of the Hours slope for males and females and not whether each simple slope is different from zero (which is what we have from the output above).
Quiz: (True of False) If both simple slopes of Hours for males and females are significantly different from zero, it implies that the interaction of Hours*Gender is not significant.
Answer: False. The test of simple slopes is not the same as the test of the interaction, which tests the difference of simple slopes.
To test the difference in slopes, we add pwcompare(effects) to tell margins that we want the pairwise difference in the simple slope of Hours for females versus males, requesting the adjusted 95% confidence interval and p-value along the way.
margins gender, dydx(hours) pwcompare(effects)
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
---------------------------------------------------------------------------------
| Contrast Delta-method Unadjusted Unadjusted
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
----------------+----------------------------------------------------------------
hours |
gender |
female vs male | 1.723931 1.897895 0.91 0.364 -2.000906 5.448768
---------------------------------------------------------------------------------
What do we notice about the p-value and the estimate? Recall from our summary table, this is exactly the same as the interaction, which verifies that we have in fact obtained the interaction coefficient $\hat{b}_3$. The only difference is that the sign is flipped because we are taking female – males (females have higher Hours slopes) whereas the interaction takes male – female. Take a look a the shortened summary table below and verify the p-value and the sign of the coefficient highlighted in red.
--------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
... (output omitted) ...
gender#c.hours |
male | -1.723931 1.897895 -0.91 0.364 -5.448768 2.000906
|
_cons | 3.334652 2.73053 1.22 0.222 -2.024328 8.693632
--------------------------------------------------------------------------------
Quiz: (True of False) The command margins gender, dydx(hours) requests the simple effect of Gender split by levels of Hours.
Answer: False. We are not obtaining the simple effect of Gender but simple slopes of Hours. The statement dydx(hours) indicates the simple slope we are requesting. Since gender is categorical, it comes before the comma which means we want the simple slope of Hours by Gender.
Quiz: (True of False) The command margins gender, dydx(hours) pwcompare(effects) requests pairwise differences in the predicted values of Hours for females versus males.
Answer: False, this is the pairwise difference in the slope of Hours for females versus males. Recall that dydx(hours) obtains simple slopes and at obtains predicted values.
Exercise
Relevel gender using ib#. so that male is now the reference group, refit the regress model for Weight Loss with the interaction of Hours by Gender; and use margins to obtain the simple effects.
a) Spell out the new regression equation using a dummy code for gender.
b) Interpret each of the coefficients in the new model.
c) What is the main difference in the output compared to using $D_{male}$? What does the naming convention in the coefficient table represent? Note you should get output from regress and margins that looks like this
--------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------+----------------------------------------------------------------
hours | 1.591136 1.3523 1.18 0.240 -1.062908 4.245181
|
gender |
female | -3.571061 3.914762 -0.91 0.362 -11.25423 4.11211
|
gender#c.hours |
female | 1.723931 1.897895 0.91 0.364 -2.000906 5.448768
|
_cons | 6.905713 2.805274 2.46 0.014 1.400039 12.41139
--------------------------------------------------------------------------------
Expression : Linear prediction, predict()
dy/dx w.r.t. : hours
---------------------------------------------------------------------------------
| Contrast Delta-method Unadjusted Unadjusted
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
----------------+----------------------------------------------------------------
hours |
gender |
female vs male | 1.723931 1.897895 0.91 0.364 -2.000906 5.448768
---------------------------------------------------------------------------------
Answers: a) $\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1 \mbox{Hours} + \hat{b}_2 D_{female}+ \hat{b}_3 \mbox{Hours}*D_{female}$, b) $\hat{b}_0= 6.906$ is the intercept for males, $\hat{b}_1 = 1.59$ is the Hours slope for males, $\hat{b}_2=-3.57$ is the difference in weight loss between female versus males at Hours=0, and $\hat{b}_3=1.72$ is the additional slope for females, which makes $\hat{b}_1+\hat{b}_3=3.31$ the female Hours slope. c) margins output shows that the signs are now consistent with regress. The appearance of female in the regression output means that we are using $D_{female}$ and males now belong to the omitted or reference group.
(Optional) Flipping the moderator (MV) and the independent variable (IV)
An interaction is symmetric, which means we can also flip the moderator (gender) so that gender is now the categorical IV and Hours is now the MV. This will reveal to us why $\hat{b}_2$ is the effect of Gender at Hours = 0. The interaction model is exactly the same, but we decompose the interaction differently. Let’s recall the regression model where we make females the reference group.
regress loss c.hours##ib2.gender
Suppose we want to see how the effect of Gender (IV) varies by levels of Hours (MV). Since Hours is continuous, it means we can hypothetically choose an unlimited number of values. For simplicity, let’s choose three plausible level of Hours: 0, 2, and 4.
The simple effect of Gender is the difference of two predicted values. In Stata, obtaining simple effects is the same as obtaining simple slopes, we can use the option dydx(gender) even if gender is binary. Then we can specify that we want the simple effect of Gender at the three levels of Hours using at(hours=(0 2 4)).
margins, dydx(gender) at(hours=(0 2 4))
Quiz: (True or False) The margins option dydx(gender) at(hours=(0 2 4)) specifies the predicted weight loss for males and females at Hours=0, 2 and 4.
Answer: False, dydx(gender) requests simple effects of gender, which is the difference of the predicted value of males versus females at a particular level of Hours.
The output we obtain from margins is the following:
Expression : Linear prediction, predict()
dy/dx w.r.t. : 2.gender
1._at : hours = 0
2._at : hours = 2
3._at : hours = 4
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.gender |
_at |
1 | 3.571061 3.914762 0.91 0.362 -4.11211 11.25423
2 | .1231992 .937961 0.13 0.896 -1.717657 1.964056
3 | -3.324663 3.905153 -0.85 0.395 -10.98898 4.33965
-------------+----------------------------------------------------------------
2.gender | (base outcome)
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
Note that in this case, 2.gender is the (base outcome). We can verify from the output that for Hours=0, the effect 3.571 matches the $\hat{b}_2$ coefficient, male, confirming that the interpretation of this coefficient is the Gender effect at Hours = 0. From our other simple effects we can see that as Hours increases, the male versus female difference becomes more negative (females are losing more weight than males).
Quiz: (True or False) Suppose we want to use $D_{female}$ (i.e., male is the reference group). If we specified ib1.gender in regress and then the requested margins, dydx(gender) we would get the female – male difference, which corresponds to the coefficient of $D_{female}$.
Answer: True. By specifying ib1.gender, the (base outcome) in the margins output would be 1.gender which corresponds to Males. Then the simple effect would be females – males, which corresponds to the $D_{female}= -3.57$ coefficient and is exactly opposite in sign to the regression where we used $D_{male}$.
Take the quiz below to make sure you understand why we don’t see a significant interaction for gender#c.hours.
Quiz: If the difference of the simple effects for gender (males versus females) is growing more negative as Hours increases, why isn’t our overall interaction significant? (Hint: look at the p-values and standard errors of each simple effect).
Answer: Although the simple effect of Gender change as Hours varies, the standard errors are so big that we cannot statistically conclude a difference. See the plot below for the large overlap in confidence intervals.
Plotting the continuous by categorical interaction
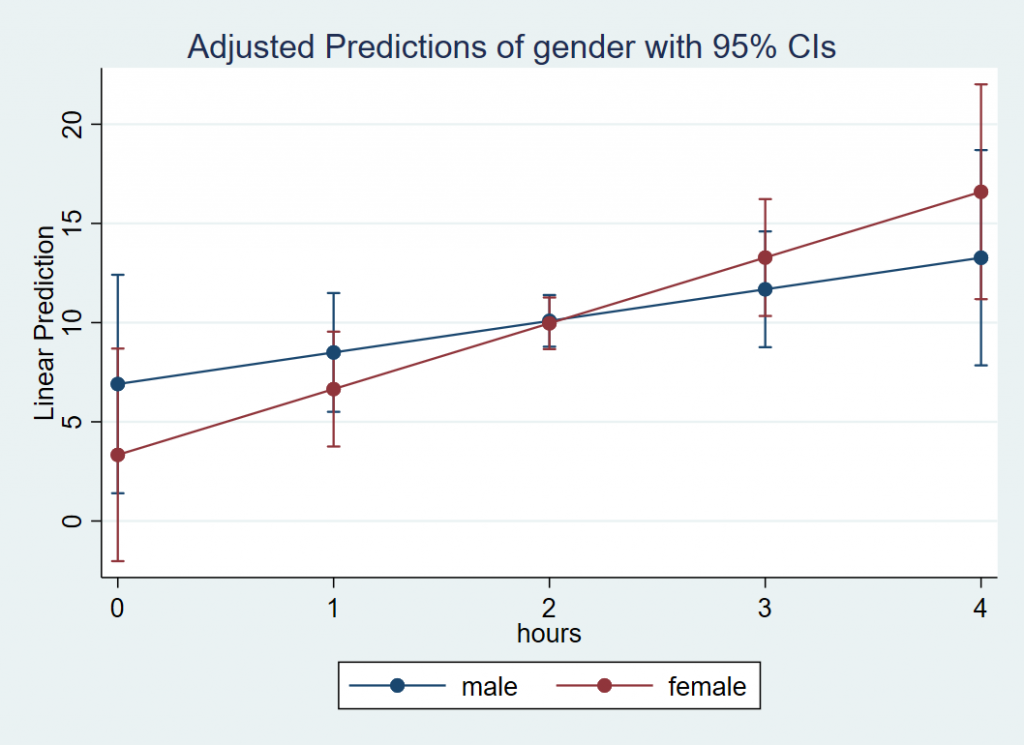
To see why the interaction is not significant, let’s visualize it with a plot. Thankfully, this is easy to accomplish using marginsplot. First we specify the margins command. We want the x-axis to indicate ranges of Hours between 0 and 4 by increments of 1 using at(hours=(0 1 2 3 4). Since Gender is a categorical variable, it comes before the comma. Stata will automatically know to use the categorical variable as the moderator that separates the lines.
margins gender, at(hours=(0 1 2 3 4)) marginsplot
Quiz: What is an equivalent way to specify the margins command above, so that we are clear that gender is the moderator?
Answer: margins, at(hours=(0 1 2 3 4)) over(gender)
The resulting figure is shown below:
Although it looks like there’s a cross-over interaction, the large overlap in confidence intervals (especially near Hours=2) suggests that the slope of Hours is not different between males and females. We confirm that the standard error of the interaction coefficient (1.898) is large relative to the absolute value of the coefficient itself (1.724).
Quiz: (True or False) Looking at the plot, since Hours is on the x-axis it is the IV and Gender separates the lines so it is the moderator (MV).
Answer: True.
Categorical by Categorical
Now that we understand how one categorical variable interacts with an IV, let’s explore how the interaction of two categorical variables is modeled. From our previous analysis, we found that there are no gender differences in the relationship of time spent exercising and weight loss. Perhaps females and males respond differently to different types of exercise (here we make gender the IV and exercise type the MV). The question we ask is, does type of exercise (W) moderate the gender effect (X)? In other words, do males and females lose weight differently depending on the type of exercise they engage in? Just as before, we must dummy code gender into $D_{male}$ and $D_{female}$, and we choose to omit $D_{female}$, making females the reference group. The difference between this model and the previous model is that we have two categorical variables, where the IV is gender and the MV is now exercise type: jogging, swimming and control group “reading”.
In order to create the dummy codes for exercise type (labeled prog in the data), recall that we have as many dummy codes as there are categories, but we retain only $k-1$ of them. In this case, we have $D_{jog} = 1$ if jogging, $D_{swim} = 1$ if swimming, and $D_{read} = 1$ if reading. It makes sense to make our control group the reference group, so we choose to omit $D_{read}.$ Therefore we retain $D_{male}$ for males, and $D_{jog}$ and $D_{swim}$ which correspond to jogging and swimming.
To see why the dummy code for reading is redundant, suppose we know that for a particular person $D_{jog}=0$, $D_{swim}=0$. Since this person is not in the jogging or swimming condition, we can conclude that this person is in the reading condition. Therefore, knowing $D_{read}=1$ provides no additional information from knowing only $D_{jog}=0$ and $D_{swim}=0$. Here is the exhaustive list of all membership categories using just jogging and swimming dummy codes:
- $D_{jog}=1,D_{swim}=0$: the participant is in the jogging condition.
- $D_{jog}=0,D_{swim}=1$: the participant is in the swimming condition.
- $D_{jog}=0,D_{swim}=0$: the participant is not in jogging and not in swimming, therefore she must be in reading.
- $D_{jog}=1,D_{swim}=1$: participant is in both jogging and swimming, we assume this is impossible, since the participant must be exclusively in one of the groups.
We are now ready to set up the interaction of two categorical variables. Since the interaction of two IV’s is their product, we would multiply the included dummy codes for Males by the included dummy codes for Exercise. Since $D_{male}$ is included for Gender and $D_{jog}$ and $D_{swim}$ are included for Exercise, their products are $D_{male} *D_{jog}$ and $D_{male} *D_{swim}$. Including the product terms and the lower order terms in our model we have:
$$\hat{\mbox{WeightLoss}}= \hat{b}_0 + \hat{b}_1 D_{male} + \hat{b}_2 D_{jog} + \hat{b}_3 D_{swim} + \hat{b}_4 D_{male}*D_{jog} + \hat{b}_5 D_{male}*D_{swim}$$
Before fitting this model in Stata, we have to make a choice about which category to make the reference (or omitted group). Since we are using $D_{male}$ we are making gender=2 or Females the reference group. How about for the second categorical variable prog. Let’s explore the frequency table, first with the label and second without the label.
tab prog
prog | Freq. Percent Cum.
------------+-----------------------------------
jog | 300 33.33 33.33
swim | 300 33.33 66.67
read | 300 33.33 100.00
------------+-----------------------------------
Total | 900 100.00
tab prog, nolabel
prog | Freq. Percent Cum.
------------+-----------------------------------
1 | 300 33.33 33.33
2 | 300 33.33 66.67
3 | 300 33.33 100.00
------------+-----------------------------------
Total | 900 100.00
Since our goal is to use $D_{jog}$ and $D_{swim}$ in our regression, we know we want to omit or set as the base reference group prog = read or 3. Not that in Stata i. notation does not distinguish a binary and categorical variable with more than two categories. No matter how many categories $k$, Stata requires only one i. statement; it knows internally to fit $k-1$ dummy codes into your regression model omitting the reference category. Therefore we only need to put ib2.gender and ib3.prog into our regression model.
Quiz: T/F When we specify ib2.prog Stata internally creates two dummy variables for Categories 1 and 3 (i.e, jogging and reading) and omits Category 2 (i.e., swimming).
Answer: True.
Now that we’ve defined our reference groups using ib#., we are ready to fit the categorical by categorical interaction model in Stata with the following code:
regress loss ib2.gender##ib3.prog
Equivalently, you can specify the single # notation with the following. Note that Stata will automatically know to relevel the simple effects based on the interaction.
regress loss i.gender i.prog ib2.gender#ib3.prog
Quiz: T/F We can also specify regress loss gender prog ib2.gender#ib3.prog as equivalent syntax.
Answer: False. Without the i. prefix for the simple effects, Stata treats gender and prog as continuous variables despite the correct ib#. specification in the interaction term.
From the syntax above we obtain the following shortened output:
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender |
male | -.3354569 .7527049 -0.45 0.656 -1.812731 1.141818
|
prog |
jog | 7.908831 .7527049 10.51 0.000 6.431556 9.386106
swim | 32.73784 .7527049 43.49 0.000 31.26057 34.21512
|
gender#prog |
male#jog | 7.818803 1.064486 7.35 0.000 5.729621 9.907985
male#swim | -6.259851 1.064486 -5.88 0.000 -8.349033 -4.170669
|
_cons | -3.62015 .5322428 -6.80 0.000 -4.66474 -2.575559
------------------------------------------------------------------------------
There are two interaction terms, one for male by jogging and the other for male by swimming, and both of them are significant. Let’s interpret each of the terms in the model:.
- $\hat{b}_0$
_cons: the intercept, or the predicted weight loss when $D_{male} = 0$ and $D_{jog}=0, D_{swim}=0$ (i.e., the intercept for females in the reading program) - $\hat{b}_1$
male: the simple effect of males for $D_{jog}=0, D_{swim}=0$ (i.e., the male – female weight loss in the reading group). - $\hat{b}_2$
jog: the simple effect of jogging when $D_{male} = 0$ (i.e., the difference in weight loss between jogging versus reading for females). - $\hat{b}_3$
swim: the simple effect of swimming when $D_{male} = 0$ (i.e., the difference in weight loss between swimming versus reading for females). - $\hat{b}_4$
male#jog: the interaction of $D_{male}$ and $D_{jog}$, the male effect (male – female) in the jogging condition versus the male effect in the reading condition. Also, the jogging effect (jogging – reading) for males versus the jogging effect for females. - $\hat{b}_5$
male#swim: the interaction of $D_{male}$ and $D_{swim}$, the male effect (male – female) in the swimming condition versus the male effect in the reading condition. Also, the swimming effect (swimming- reading) for males versus the swimming effect for females.
The last two coefficients are the most difficult to interpret. We can think of $\hat{b}_4$ as the additional male effect of going from reading to jogging and $\hat{b}_5$ as the additional male effect going from reading to swimming:
- $\hat{b}_1+\hat{b}_4$
male+male#jogis the simple effect of males in the jogging group, - $\hat{b}_1+\hat{b}_5$
male+male#swimis the simple effect of males in the swimming group.
We can confirm this is true for jogging if we subtract the interaction term $\hat{b}_4$, the additional male effect for jogging, from $(\hat{b}_1+\hat{b}_4)$. Then $(\hat{b}_1+\hat{b}_4) – \hat{b}_4 = \hat{b}_1$ which from above we know is the male effect in the reading group.
Quiz: Use the coefficients from the categorical by categorical interaction to derive the female (female – male) effect for the swimming group. (Hint: flip the sign of the coefficient)
Answer: $-\hat{b}_1+(-\hat{b}_5)=-(\hat{b}_1+\hat{b}_5)=-(-0.336+(-6.26))=6.60.$
Simple effects in a categorical by categorical interaction
Although the coefficients in the categorical by categorical regression model are a bit difficult to interpret, it is surprisingly easy to obtain simple effects from margins. First we want to obtain the predicted values for each combination of Gender and Program. Typically, for continuous variables this would require the at option. However, recall that categorical variables come before the comma in margins and since both gender and prog are categorical, we omit the at option. Since gender and prog are both defined to be categorical with the corresponding ib#., the syntax is as follows:
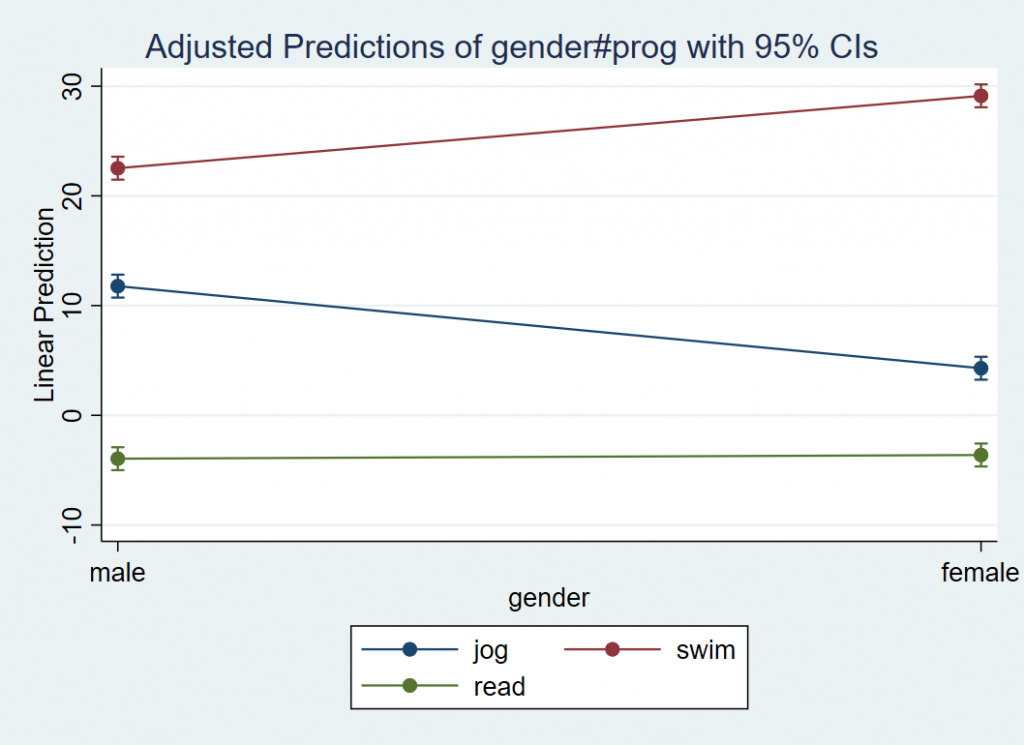
margins gender#prog
This will obtain the predicted values at each level combination of gender and prog .
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender#prog |
male#jog | 11.77203 .5322428 22.12 0.000 10.72744 12.81662
male#swim | 22.52238 .5322428 42.32 0.000 21.47779 23.56697
male#read | -3.955606 .5322428 -7.43 0.000 -5.000197 -2.911016
female#jog | 4.288681 .5322428 8.06 0.000 3.244091 5.333272
female#swim | 29.11769 .5322428 54.71 0.000 28.0731 30.16228
female#read | -3.62015 .5322428 -6.80 0.000 -4.66474 -2.575559
------------------------------------------------------------------------------
These are the predicted values of weight loss for all combinations of Gender and Exercise. For example, females in the reading program have an estimated weight gain of 3.62 pounds, whereas males in the swimming program have an average weight loss of 22.52 pounds (how nice if this were true!).
Exercise
Try to reproduce each predicted value from margins using the coefficient table alone. Do you notice a pattern for the coefficient terms?
Answer: In order of the table: \begin{eqnarray} (\hat{b}_0) & & &=& -3.62 \\ (\hat{b}_0 + \hat{b}_1) &=& -3.62 + (-0.336) &=&-3.96 \\ (\hat{b}_0) + \hat{b}_2 &=& -3.62 + 7.91&=&4.29 \\ (\hat{b}_0 + \hat{b}_1) + \hat{b}_2 + \hat{b}_4 &=& -3.62 + (-0.336) + 7.91 + 7.82&=&11.77 \\ (\hat{b}_0)+\hat{b}_3 &=& -3.62 + 32.74&=&29.12 \\ (\hat{b}_0+\hat{b}_1)+\hat{b}_3+\hat{b}_5 &=& -3.62 + (-0.336)+32.74+(-6.25)&=& 22.53 \end{eqnarray}
There are many possible patterns, but one pattern is to start with $(\hat{b}_0)$ for females, $(\hat{b}_0+\hat{b}_1)$ for males, then add on additional terms. For females, the additional terms do not involve interaction terms, but for males it does. For example, for females in the jogging group, start with $\hat{b}_0$ which is predicted weight loss for females in the reading group, then add on the additional effect of jogging for females which is $\hat{b}_2$. For males in the jogging group, first obtain the predicted value of males in the reading group $(\hat{b}_0+\hat{b}_1)$, then add $(\hat{b}_2 + \hat{b}_4)$ which is the additional jogging effect for males ($\hat{b}_4$ is the jogging versus reading effect above the jogging versus reading effect for females).
In order to understand the interaction, we need to obtain the simple effects which are differences of the predicted values. This can be accomplished using the dydx option after margins. The key is to know which independent variable (IV) you want to the make the moderator (MV). Let’s suppose that our interest to see how the Gender effect (IV) varies by levels of the intervention program (MV). The hypothetical code is then margins mv, dydx(iv). Note that both the MV and IV need to be categorical for this syntax to work. In our example, we have
margins prog, dydx(gender)
which gives us the following output:
Expression : Linear prediction, predict()
dy/dx w.r.t. : 1.gender
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.gender |
prog |
jog | 7.483346 .7527049 9.94 0.000 6.006072 8.960621
swim | -6.595308 .7527049 -8.76 0.000 -8.072582 -5.118033
read | -.3354569 .7527049 -0.45 0.656 -1.812731 1.141818
-------------+----------------------------------------------------------------
2.gender | (base outcome)
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
Recall that we specified ib2.gender in regress which means Female is our reference group; the comparisons in the output table are for Males – Females. We see that the male effect for jogging and swimming are significant at the 0.05 level (with no adjustment of p-values), but not for the reading condition. Additionally, males lose more weight in the jogging condition (positive) but females lose more weight in the swimming condition (negative).
Quiz: (True or False) The interaction is the male effect for a particular exercise type.
Answer: False. See below.
The male effect alone does not capture the interaction. The interaction is the difference of simple effects. Going back to the output from regress loss ib2.gender##ib3.prog, let’s see if we can recreate $\hat{b}_5=-6.26$ which is the interaction of male by swimming using the output from contrast.
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
... (output omitted) ...
male#swim | -6.259851 1.064486 -5.88 0.000 -8.349033 -4.170669
|
_cons | -3.62015 .5322428 -6.80 0.000 -4.66474 -2.575559
------------------------------------------------------------------------------
Recall that the interaction is the difference of simple effects. In this case, we want the difference in the male effect (males vs. females) in the swimming condition and the male effect in the reading condition. From margins, recall that the gender effect for swimming is -6.59 and the gender effect for reading is -0.335. Then the difference of the two simple effects is -6.595-(-0.335) = -6.26, which matches our output from the original regression. We verify therefore that the interaction is the pairwise difference of the male effects (male-female) for swimming versus reading. It is essentially a difference of differences.
Exercise
Find the interaction that is not automatically generated by the original regression output and obtain its effect by manually calculating the difference of differences using the output from margins. Confirm your answer with a regression (Hint: you need to change the reference group).
Answer: $7.48-(-6.595) = 14.08$, the interaction of jogging versus swim by gender. Running regress loss ib2.gender##ib2.prog should produce the following shortened code:
------------------------------------------------------------------------------
loss | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender |
male | -6.595308 .7527049 -8.76 0.000 -8.072582 -5.118033
|
prog |
jog | -24.82901 .7527049 -32.99 0.000 -26.30628 -23.35173
read | -32.73784 .7527049 -43.49 0.000 -34.21512 -31.26057
|
gender#prog |
male#jog | 14.07865 1.064486 13.23 0.000 11.98947 16.16784
male#read | 6.259851 1.064486 5.88 0.000 4.170669 8.349033
|
_cons | 29.11769 .5322428 54.71 0.000 28.0731 30.16228
------------------------------------------------------------------------------
Optional Exercise: We have been focusing mostly on the gender effect (IV) split by exercise type (MV). However, an interaction is symmetric which means we can also look at the effect of exercise type (IV) split by gender (MV). Obtain the same interaction term using margins with gender as the moderator.
Answer to Optional Exercise: margins gender, dydx(prog), $-10.75-(-24.83) = 14.08.$ This is the difference in the jogging effect for males versus females (difference of differences), treating Gender as the MV. In the previous example, we treated Exercise as the MV so that the interpretation is the difference in the gender effect for jogging vs. reading. The output should look like the following
Expression : Linear prediction, predict()
dy/dx w.r.t. : 1.prog 3.prog
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.prog |
gender |
male | -10.75036 .7527049 -14.28 0.000 -12.22763 -9.273081
female | -24.82901 .7527049 -32.99 0.000 -26.30628 -23.35173
-------------+----------------------------------------------------------------
2.prog | (base outcome)
-------------+----------------------------------------------------------------
3.prog |
gender |
male | -26.47799 .7527049 -35.18 0.000 -27.95526 -25.00072
female | -32.73784 .7527049 -43.49 0.000 -34.21512 -31.26057
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
Plotting the categorical by categorical interaction
Finally, the best way to understand an interaction is to plot it. The marginsplot command follows margins and plots the independent variable (IV) on the x-axis and splits the lines by levels of the moderating variable (MV). Assuming you’ve previously run regress and both variables are categorical, the hypothetical syntax is margins iv#mv. For our case, we want prog to be our moderator, so we specify the following syntax
margins gender#prog marginsplot
Quiz: (True or False) The code margins prog#gender tells marginsplot that we want prog on the x-axis with lines corresponding to levels of gender.
Answer: True.
We obtain the following interaction plot:
Here we see the results confirming the predicted values and simple effects we found before. Each point on the plot is a predicted value and each line or connection of two points is a simple effect. Exercise type (prog) is the moderator of the gender effect (gender), and we see a negative effect for swimming (females lose more weight swimming) and a positive effect for jogging (men lose more weight jogging). Females and males lose about the same amount of weight for the reading condition. Since we have simple effects rather than simple slopes, some researchers prefer bar graphs for representing categorical changes in effects.
Quiz: How would we plot exercise type along the x-axis split by gender? Which plot makes more sense to you?
Answer: margins prog#gender followed by marginsplot. The independent variable (IV) should always be the focus of the study, and the moderator (MV) is the variable that changes the primary relationship of the IV on the DV. If exercise type is on the x-axis then the researcher is primarily interested in how exercise type influences weight loss but is also interested in whether males and females respond differently to various exercise modalities.
Conclusion
As a researcher, the question you ask should determine which interaction model you choose. Hopefully we have exhausted all the types of research questions you can ask with the interaction of two variables. Recall that coefficients for IV’s interacted with an MV are interpreted as simple effects (or slopes) fixed at 0 of the MV, whereas coefficients for IV’s not interacted with others are main effects (or slopes) meaning that its effect does not vary by the level of another IV. The interaction itself always involves differences of simple effects or slopes. Researchers who are just starting out with interaction hypotheses often confuse testing the simple slope (or effects) against zero versus the interaction, which tests whether the difference of simple slopes (or effects) are different from zero. Another common point of confusion is the idea of a predicted value versus a simple slope slope (or effect). A predicted value is a single point on the graph, whereas a simple slope (or effect) is a difference of two predicted values. Furthermore, an interaction is a difference of two simple slopes (or effects). To summarize these concepts geometrically:
- Predicted values are points on the graph.
- Simple effects or slopes are the difference between two predicted values (i.e., two points).
- Interactions are the difference between simple effects of slopes;
- for an interaction involving a continuous IV, it’s the difference of two slopes (i.e., two lines)
- for a categorical by categorical interaction, the interaction is the difference in the differences of the predicted values (i.e. four points).
It may be instructive to plot the regression and rephrase your research question using the geometric representations of the graph.
Final Exercise
Return to a plot in each type of interaction and identify four predicted values, two corresponding simple slopes or effects and the corresponding interaction.
Thank you taking the time to read this seminar. We hope the material will help you in your research endeavors.