Note: A PowerPoint presentation of this webpage can be downloaded here. A file of just the SAS code is available here. The dataset used in this seminar can be found here: exercise.
Table of Contents
-
- Introduction
- Purpose of this seminar
- Main effects vs interaction models
- PROC PLM
- Dataset used in the seminar
- Linear regression, continuous-by-continuous interaction
- The model
- Example model
- The estimate statement for simple slopes
- Calculating simple slopes and testing them for significance
- Comparing simple slopes
- Graphing simple slopes
- Linear regression, quadratic effect
- The model
- Example model
- Calculating simple slopes and testing them for significance
- Comparing simple slopes
- Graphing quadratic effects
- Linear regression, categorical-by-continuous interaction
- The model
- Categorical predictors and dummy variables
- Example model
- Calculating simple slopes and testing them for significance
- Comparing simple slopes
- Graphing simple slopes
- The model
- Linear regression, categorical-by-categorical interaction
- The model
- Interactions of categorical predictors as dummy variables
- Example model
- Estimating simple effects with the
slicestatement - Estimating simple effects with the
lsmestimatestatement - Comparing simple effects
- Graphing simple effects
- The model
- Linear regression, 3-way categorical-categorical-continuous interaction
- The model
- Example model
- Simple slopes focused analysis
- What are the simple slopes in each pairing of levels of the 2 factors?
- Are the conditional interactions of one factor and the continuous variable significant within each level of the other factor?
- Are the conditional interactions different from each other?
- Graphing simples slopes analysis of the 3-way interaction
- Simple effect focused analysis
- What are the simple effects of one factor across levels of the other factor at selected values of the covariate
- Are the conditional interactions of the 2 factors signfiicant at selected values of the covariate?
- Are the conditional interactions different?
- Graphing the simple effects analysis of the 3-way interaction
- Logistic regression
- Background
- Example model
- Calculating and graphing simple odds ratios
- Comparing simple odds ratios and interpreting exponentiated interaction coefficients
- simple effects analysis and predicted probabilities
- Conclusion: general guidelines for coding in proc plm
- Introduction
1. Introduction
1.1 Purpose of this seminar
Statistical regression models estimate the effects of independent variables (IVs, also known as predictors) on dependent variables (DVs, also known as outcomes). At times, we model the modification of the effect of one IV by another IV, often called the moderating variable (MV). This effect modification is known as a statistical interaction. For example, we may model the effect of number of minutes of exercise (IV) on weight loss (DV) that is modified by 3 different exercise types (MV). Interaction variables are generated by multiplying the IV and the MV together, and this resulting product variable is then entered into the regression, typically along with the IV and MV. The resulting interaction regression coefficient represents a test of whether the effect of the IV depends on the other MV (to be clear, the regression model does not distinguish between the IV and MV, as the effect of the MV is also modified by the IV and is represented by the same interaction coefficient). Although certainly important, this test is usually not sufficient to understanding and interpreting fully the interaction, which would require us to know the magnitude, direction, and significance of the effect of the IV at different levels of the MV. The conditional effect of a categorical IV at a specific level of the MV is known as a simple effect (sometimes simple main effect) while the conditional effect of continuous IV is often called a simple slope.
This seminar outline methods for the interpretation of a statistical interaction via analysis of the conditional effects that comprise the interaction. Specifically, this seminar covers how to:
-
-
- Calculate simple effects/slopes and test them versus zero for significance: Typically, only the conditional effect at the reference level of the MV is directly estimated by regression and tested for significance. Additional steps are usually needed to calculate the effect at other levels of the MV, and to test these slopes against zero.
- Test differences among simple effects/slopes: Tests of the interaction coefficients versus zero are tests of differences between the effects at the reference level of the MV and effects at other levels of the MV. However, tests between slopes at these other levels of the MV are often interesting as well.
- Graph simple effects/slopes: Visual representation of the interaction usually provides the easiest and quickest interpretation.
-
1.2 Main effects vs interaction models
In a main-effects model, each IV’s effect on the DV is essentially estimated as the average effect of that IV across levels of all other IVs. The resulting averaged effect is constant across levels of the other IVs. For example imagine a main-effects model where we try to predict someone’s weight based on that person’s sex and height:
$$weight = \beta_0 + \beta_{s}SEX + \beta_{h}HEIGHT$$
The coefficient describing the effect of height on weight, \(\beta_{h}\), is a weighted average of the two height coefficients for males and females, had we modeled them separately. The resulting main effect of height will be the same for both males and females. However, it is reasonable in such a model to wonder if the two height effects are different by sex, and should be allowed to vary by the model. To assess whether the height effects are different, we add an interaction to the model.
$$weight = \beta_0 + \beta_{s}SEX + \beta_{h}HEIGHT + \beta_{sh}SEX*HEIGHT$$
Important: In an interaction model, the coefficients representing the component individual (“main-effects”) terms are no longer interpreted as main effects, but instead as the simple effect when the interacting variable is equal to 0. Thus, \(\beta_{h}\) represents the effect of \(HEIGHT\) when \(SEX=0\), or the effect of \(HEIGHT\) for males. Similarly \(\beta_{s}\) represents the effect of being female vs. male when \(HEIGHT=0\) (not a realistic height!). The \(\beta_{sh}\) coefficient represents how much \(\beta_{s}\) and \(\beta_{h}\) change per unit-increase in \(HEIGHT\) and \(SEX\), respectively. Given \(SEX=0\) for males and \(SEX=1\) for females, we can construct regression equations for males and females by substituting in these (0,1) values to see this relationship explicitly:
$$weight_{males} = \beta_0 + \beta_{s}(0) + \beta_{h}HEIGHT + \beta_{sh}(0)*HEIGHT$$ $$weight_{males} = \beta_0 + \beta_{h}HEIGHT$$
$$weight_{females} = \beta_0 + \beta_{s}(1) + \beta_{h}HEIGHT + \beta_{sh}(1)*HEIGHT$$ $$weight_{females} = \beta_0 + \beta_{s} + \beta_{h}HEIGHT + \beta_{sh}HEIGHT$$ $$weight_{females} = \beta_0 + \beta_{s} + (\beta_{h} + \beta_{sh})HEIGHT$$
In the above equations we can see that \(HEIGHT\) has a different effect for males, \(\beta_{h}\), from the effect for females, \(\beta_{h} + \beta_{sh}\). The interaction regression coefficient thus represents deviations or changes from a reference effect — above, it represents the difference between the height effect for males and females, as a unit-increase on \(SEX\) represents changing from males to females. This interpretation of the interaction coefficient holds when the component main effects are entered with the interaction variable (i.e, the interpretation of the interaction variable coefficient changes if the interaction is entered into the regression alone).
1.3 PROC PLM
This seminar relies heavily on proc plm to estimate, compare and plot the conditional effects of interactions. We first introduce proc plm in general.
Proc plm performs various analyses and plotting functions after an initial regression model is fit, including custom hypothesis testing of model effects and contrasts, calculating predicted values of the outcome (scoring), and plotting these predictions. Unlike most other SAS procedures, proc plm does not take a dataset as input, but instead uses an item store, which contains information about the regression model fit in another procedure. The item store can be created by many of the commonly used regression procedures, such as glm, genmod, logistic, phreg, mixed, glimmix and several others, through a store statement where we simply need to supply the name of an item store. This name for the item store is then supplied to the restore option (previously source in earlier versions of SAS) on the proc plm statement as input.
The following proc plm statements will be used in this seminar:
-
-
estimate: used to estimate means, contrasts, and for this seminar, simple slopes, conditional interactions, and differences among them, by specifying linear combinations of the model coefficients; very flexible — all calculations in this seminar can be made throughestimatestatements, though often requiring more codingslice: compares margins means, which for this seminar serves to estimate simple effectslsmestimate: a hybrid of theestimatestatement and thelsmeansstatement used in this seminar to estimate simple effects by specifying differences between meanslsmeans: used to estimate marginal means and to calculate differences among themeffectplot: used to plot predicted values of the outcome across a range of values of one or two predictors, for this seminar to visualize simple effect, simple slopes, and conditional interactions. If other predictors are in the model,effectplotwill fix their value, by default at the mean for continuous predictors and at the reference level for categorical predictors.
-
Each of the statements above, particularly estimate and lsmeans can often be found in the the procedures which created the item store . So why use proc plm instead of the version of these statements in the regression procedures?
-
-
- Once we are happy with our regression model, as we edit and add code for the analysis of the interaction, the model does not need to be refit each time we run the code. The model is stored in the items store. This can save a lot of time and creates much less output that we would otherwise discard had we run these in regression procedures
- These statements often have more functionality (options) in
proc plmthan in other procedures.
-
1.4 Dataset used in the seminar
The dataset used in the seminar can be found here: exercise. The dataset consists of data describing the amount of weight loss achieved by 900 participants in a year-long study of 3 different exercise programs, a jogging program, a swimming program, and a reading program which serves as a control activity. Researchers were interested in how the weekly number of hours subjects chose to exercise predicted weight loss. Variables used in this tutorial include:
-
-
- loss: a continuous, normally distributed variable describing the average weekly weight loss for participants. Positive scores denote weight loss, while negative scores denote weight gain. Used as the outcome in most of the regression models in this seminar.
- hours: a continuous variable describing the average number of weekly hours of exercise. Used as the primary continuous predictor in this seminar.
- effort: a continuous variable ranging from 0 to 50, which is an average of weekly subject-reported effort scores, also ranging from 0 to 50, with 0 denoting minimal physical effort and 50 denoting maximum effort.
- prog: A 3-category variable detailing which exercise progrm the subject followed, either jogging=1, swimming=2, or reading=3 (control).
- female: A binary categorical variable denoting gender, male=0, female=1.
- satisfied: a binary (0/1) variable denoting the subject’s satisfaction (satisfied=1) or dissatisfaction (satisfied=0) with the amount of weight lost.
-
The dataset does not come with formatted values for prog or female, so if the user would like to add formats, use the following code:
proc format;
value prog 1 = 'jogging'
2 = 'swimming'
3 = 'reading';
value female 0 = 'male'
1 = 'female';
run;
data exercise;
set "C:/path/to/file/exercise";
format prog prog.;
format female female.;
run;
The dataset is referred to as exercise in the SAS code throughout this seminar.
2 Linear regression, continuous-by-continuous interaction
2.1 Linear regression, continuous-by-continuous interaction: the model
We will first look at how to analyze the interaction of two continuous variables. We often call the effect of a continuous predictor on the the DV a “slope”. (When we use the phrase “slope of \(X\)”, we mean the change in the outcome per unit change in \(X\)) When a continuous IV is interacted with a continuous MV, the effect of the IV at a particular level of the MV is in turn called a “simple slope”. Similarly, the effect of the MV at a particular level of the IV could also be called a “simple slope”, because the regression model is ignorant of the roles of the IV and the MV in the interpretation of the interaction. For a model with a single continuous IV, \(X\), and a single continuous MV, \(Z\), the following coefficients will be estimated:
\begin{align} Y’&=\beta_0 \\ &+ \beta_{x}X \\ &+ \beta_{z}Z \\ &+ \beta_{xz}X*Z \end{align}
Remember that when there are interactions in the model, the individual effects are not interpreted as main effects. We interpret the coefficients in this model as:
-
-
- \(\beta_0\): intercept, estimate of \(Y’\) when \(X=0\) and \(Z=0\).
- \(\beta_{x}\): simple slope of \(X\) when \(Z=0\).
- \(\beta_{z}\): simple slope of \(Z\) when \(X=0\).
- \(\beta_{xz}\): change in slope for \(X\) when \(Z\) increases by 1-unit, and change in slope for \(Z\) when \(X\) increases by 1-unit.
-
Notice we could analyze the simple slopes of \(X\) at various levels of \(Z\), which we will show, and the simple slopes of \(Z\) at various levels of \(X\), which we will not since the procedure is the same.
With a little algebra, we can derive a formula to calculate the slope of \(X\) at any value of \(Z=z\). Remember that a slope (or regression coefficient) expresses the change in the outcome per unit change in the predictor. First we will calculate the expected value of Y when \(X=0\) and \(X=1\), for any value of \(Z=z\):
$$Y’_{x=0} = \beta_0 + \beta_{x}(0) + \beta_zz + \beta_{xz}(0)*z$$ $$Y’_{x=0} = \beta_0 + \beta_zz$$ $$Y’_{x=1} = \beta_0 + \beta_{x}(1) + \beta_zz + \beta_{xz}(1)*z$$ $$Y’_{x=1} = \beta_0 + \beta_x + \beta_zz + \beta_{xz}z$$
The difference between \(Y’_{x=1}\) and \(Y’_{x=0}\) represents the change in \(Y’\) due to a unit-increase in \(X\) at a particular value of \(Z\), which is the slope of \(X\) at \(Z\):
$$Y’_{x=1} – Y’_{x=0} = \beta_0 + \beta_x + \beta_zz + \beta_{xz}z – (\beta_0 + \beta_zz)$$ $$slope_X = \beta_x + \beta_{xz}z$$
The formula implies that the slope of \(X\) when \(Z=0\) is \(\beta_x\), and that \(\beta_{xz}z\), quantifies the change in the slope of \(X\) as a result of increasing \(Z\) by \(z\) units.
The formula for calculating simple slopes and effects can also be derived by taking the partial derivative of \(Y’\) with respect the \(X\). In econometrics, this is known as the marginal effect.
$$\dfrac{\partial Y’}{\partial X} = \beta_{x} + \beta_{zx}Z$$ $$slope_{X} = \beta_{x} + \beta_{zx}Z$$
We see the same formula as before.
2.2 Linear regression, continuous-by-continuous interaction: example model
In the code below, we use PROC GLM to run a linear regression modelling the effects of \(hours\), \(effort\), and their interaction on \(loss\), to probe whether the effect of the average weekly number of hours of exercise varies with the amount of effort the subject exerts.
proc glm data=exercise; model loss = hours|effort / solution; store contcont; run;
Notice in the code above:
- The “|” symbol between hours and effort requests that both the interaction of these variables and the component main effects be entered into the regression.
- The
solutionoption requests the table of regression coefficients (parameters), which is generally useful for interpretation and quite helpful in constructing estimate statements to calculate simple slopes and effects. - The
storestatement creates an item store named “contcont”, which contains the information about the regression model needed byproc plm
Below are the regression coefficients. We see that the interaction of \(hours\) and \(effort\) is significant, p=.0362.
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| Intercept | 7.798637340 | 11.60361526 | 0.67 | 0.5017 |
| hours | -9.375681298 | 5.66392068 | -1.66 | 0.0982 |
| effort | -0.080276367 | 0.38464693 | -0.21 | 0.8347 |
| hours*effort | 0.393346795 | 0.18750440 | 2.10 | 0.0362 |
These results produce the following regression equation:
$$loss’ = 7.8 – 9.4hours – .08effort + .39hours*effort$$
One interpretation of the significant interaction of hours and effort is that the effect of the average weekly number of hours on weight loss depends on the level of effort exerted; in other words, the slope of hours depends on effort. We might now be interested in calculating the slope of hours at various levels of effort, and to test whether these slopes are significantly different from 0. For this simple slope analysis we will use the estimate statement, which we describe in general below.
2.3 The estimate statement for simple slopes
The estimate statement is used to estimate linear combinations (weighted sums) of regression coefficients. The estimate statement is quite flexible in its usage because linear combinations of regression coefficients can generate many quantities of interest: predicted values of the outcome, slopes and effects, differences in slopes and effects (interactions), contrasts between means, etc. Simple slopes are indeed linear combinations of coefficients \(slope_X = \beta_x + \beta_{xz}z\), so estimate statements provide a way to calculate these slopes as well as test them against zero. The estimate statement is available in most regression procedures and proc plm. The basic syntax of estimate statements is as follows:
estimate ‘label’ coefficient values / e
- ‘label’:an optional label describing the estimate statement
- ‘coefficient_name values’: Names of coefficients to be combined and values at which to evaluate these coefficients. Any number of model coefficients, including the intercept, can be specified. Categorical terms or interactions involving categorical predictors may require several values to be listed.
- Several estimates can be specified on a single
estimatestatements, each defined by [‘label’ coefficient values] and separated by the “,” symbol. This allows a joint test on all estimates to be performed (see section 6.2 on 3-way interactions) and will put all results in one table, as opposed to separate tables if separateestimatestatements are used. - / e: The “e” option after the
/symbol requests that SAS produce a table of the values applied to coefficients. Although this is indeed optional, we highly recommend that it always be used because at times, SAS will apply values to coefficients without user specification (see Potential Pitfall below).
The set of regression coefficients are multiplied by their corresponding values, and the resulting products are summed to form the linear combination. As an example, we will show how to estimate the predicted loss for a subject who averages 2 hours of exercise per week at an effort level of 30. The equation to calculate the predicted loss is below. The values that are multipled with the coefficients correspond to the values of our predictors and are listed in parentheses (the 1 after the intercept, 7.8, is placed to include the intercept):
$$loss’ = 7.8 – 9.38hours – .08effort + .39hours*effort$$ $$loss’ = 7.8(1) – 9.38(2) – .08(30) + .39(2)*(30)$$ $$loss’ = 7.8(1) – 9.38(2) – .08(30) + .39(60)$$
The values in the parentheses in the final equation above will be the values following the coefficients in the estimate statement. Below are the estimate statement to predict this loss and its resulting output. Notice the label and the values following the coefficients, whose names appear as they do in the regression table above.
proc plm restore=contcont; estimate 'pred loss, hours=2, effort=30' intercept 1 hours 2 effort 30 hours*effort 60 / e; run;
| Estimate Coefficients | |
|---|---|
| Effect | Row1 |
| Intercept | 1 |
| hours | 2 |
| effort | 30 |
| hours*effort | 60 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| pred loss, hours=2, effort=30 | 10.2397914 | 0.45307911 | 22.60 | <.0001 |
Notice in the code and resulting output above:
- The table of Estimate Coefficients (produced by the “
e” option) with their corresponding values matches what we wanted - The label ‘pred loss, hours=2, effort=30’ in the estimate statement appears in the Parameter column for easy identification of what is being estimated
- The “t-value” and “Pr>[t]” represent the t-statistic and resulting p-value used to test whether this estimate is equal to 0. In this case of estimating a predicted mean, this test is not really interesting, but when we estimate simple effects and slopes, it will be quite important.
2.4 Linear regression, continuous by continuous interaction: calculating simple slopes and testing them for significance
Let’s reexamine the formula for simple slopes of the IV when the moderator is continuous:
$$slope_X = \beta_x + \beta_{xz}Z$$
We can use this formula to get a formula for the simple slopes of hours (\(X\)) as a function of effort (\(Z\)), where \(\beta_{he}\) is the interaction coefficient: $$slope_{h} = \beta_{h} + \beta_{he}effort$$ $$slope_{h} = -9.38 + .39effort$$
This formula tells us that the slope of hours is -9.38 when effort=0, and increases by .393 per unit increase in effort.
Because effort is a continuous moderator, it can potentially take on an infinite number of values between 0 and 50. So how do we choose values of effort at which to evaluate the slope of hours? Two options are typically chosen. The first option is to choose substantively important values of the moderator, assuming they exist. For example, if BMI were the moderator, we might choose BMI=18.5, BMI=25, and BMI=30, which are the cutoffs for underweight, overweight, and obese classifications on the BMI scale. The second option is to use data-driven values, such as the mean of the moderator, and the mean plus or minus one standard deviation. Because there are no pre-determined substantively interesting values of our moderator effort, we will evaluate the slope of hours at the mean of effort, and the mean plus or minus one standard devation.
We will use estimate statements to calculate our simple slopes of hours at different values of effort and test them for significance. We first need to calculate the mean and standard deviation of effort. We use proc means to obtain these.
proc means data = exercise; var effort; run;
| Analysis Variable : effort | ||||
|---|---|---|---|---|
| N | Mean | Std Dev | Minimum | Maximum |
| 900 | 29.6592189 | 5.1427635 | 12.9489995 | 44.0760408 |
The values of effort at which we will calculate our simple slopes are:
\begin{align} mean_e &= 29.66 \\ meanPlusSD_e &= 29.66+5.14=34.8 \\ meanMinusSD_e &= 29.66-5.14=24.52 \end{align}
Once again, the general equation for the simple slope of hours is,: $$slope_{h} = \beta_{h} + \beta_{he}effort$$
which can be rewritten as: $$slope_{h} = \beta_{h}(1) + \beta_{he}(effort)$$
The values in parentheses are the values we will apply to the coefficients in the estimate statement code to calculate the simple slopes. The mean, and mean plus or minus one standard deviation of effort, are the values that we will apply to the \(\beta_{he}\) coefficient in the estimate statement:
proc plm restore=contcont;
estimate 'hours slope, effort=mean-sd' hours 1 hours*effort 24.52,
'hours slope, effort=mean' hours 1 hours*effort 29.66,
'hours slope, effort=mean+sd' hours 1 hours*effort 34.8 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| hours slope, effort=mean-sd | 0.2692 | 1.3493 | 896 | 0.20 | 0.8419 |
| hours slope, effort=mean | 2.2910 | 0.9151 | 896 | 2.50 | 0.0125 |
| hours slope, effort=mean+sd | 4.3128 | 1.3084 | 896 | 3.30 | 0.0010 |
From these tables we see that the slope of hours is only signficant at the mean and mean plus one standard deviation of effort. These results suggest that a certain amount of effort need be exerted in order for the number of weekly hours to make a difference in the expected weight loss.
2.5 Linear regression, continuous by continuous interaction: comparing simple slopes
There is actually no need to compare simple slopes of a continuous by continuous interaction. No matter how far apart or how close we pick values of effort, the simple slopes of hours will always be significantly different from each other if the interaction coefficient is significant, and always not significantly different if the interaction is not significant. This occurs because as we move our effort values farther apart, making the difference between the simple slopes larger, the standard error of the difference scales upward commensurately with the difference. We will demonstrate this equivalence by comparing the simple slopes of hours at effort values at the mean and at the mean minus one standard deviation.
To get the difference in simple slopes (or simple effects), we simple subtract the linear combination of coefficients for one slope from the other:
$$slope_{h@mean}-slope_{h@mean-sd} = \beta_{h} + \beta_{he}meanEffort – (\beta_{h} + \beta_{he}meanMinusSD)$$ $$slope_{h@mean}-slope_{h@mean-sd} = \beta_{hours} + \beta_{he}29.66 – (\beta_{hours} + \beta_{he}24.52)$$ $$slope_{h@mean}-slope_{h@mean-sd} = \beta_{he}5.14$$
Notice that the values for \(\beta_{hours}\) cancel to 0 so we only need to supply one coefficient, \(\beta_{he}\), and its corresponding value, 5.14.
proc plm restore=contcont; estimate 'diff slopes, mean+sd - mean' hours*effort 5.14; run;
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| diff slopes, mean+sd – mean | 2.02180253 | 0.96377262 | 2.10 | 0.0362 |
Notice that the t-value and p-value for this estimate of the difference between simple slopes match those of the hours*effort interaction coefficient in the regression table. This estimate and its standard error are both 5.14 times greater than the hours*effort parameter estimate and its corresponding, reflecting the fact that one standard deviation of effort is equal to 5.14 units of effort. In sum, this comparison, though instructive is not necessary.
2.6 Linear regression, continuous by continuous interaction: graphing simple slopes
We will now use the effectplot statment within proc plm to generate quick graphs of our simple slopes of hours across levels of effort.
Contour plots are one option for displaying the interaction of two continuous variables. They have the advantage that both continuous variables can be represented continuously on the graph, because they are plotted on the x-axis and y-axis, while the outcome is plotted as the contours. On the other hand, contour plots are not common in every field, so can be hard to interpret for some audiuences. The specification for the contour plot is simple — on the effectplot statement we request a contour plot and specify which predictors we want to appear on which axis:
proc plm source=contcont; effectplot contour (x=hours y=effort); run;
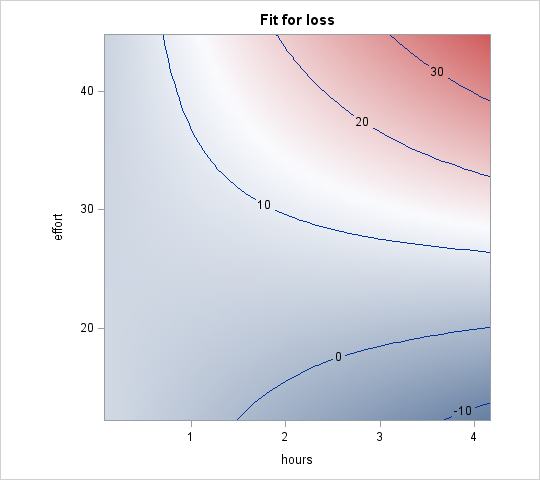
We see hours along the x-axis, effort along the y-axis, and loss, the outcome, is plotted as the contours. The bluer areas denote lower values of loss, while the redder areas denote higher values, and some contours are labeled with the corresponding value of loss. The simple slopes of hours are depicted as horizontal lines traversing the graph. At an effort level of 24.52 (mean – sd), nearly midway up the graph, we see that the horizontal line here does not change color much, reflecting a small amount of change in loss over the range of hours, or a nearly flat slope. This corresponds to the simple slope of hours of 0.2692 that was not significantly different from 0 that we calculated above. On the other hand, at an effort level of 34.8 (mean + sd), the graph changes quickly from blue to red, reflecting a large slope, confirmed by the value 4.3128 calculated above.
Note: a contour plot similar to this one (but with the observed data points plotted as well) is plotted by proc glm by default when a continuous by continuous interaction is modeled and there are no other predictors in the model. We discuss how to produce this plot in proc plm instead as more complex models will no doubt arise.
Perhaps a more commonly chosen option to plot the interaction of 2 continuous variables is to plot the slope of the IV as lines at selected levels of the moderator. We will use the fit graph in the effectplot statement to produce these line plots. Typically, a fit graph will plot predicted values of the outcome across the range of a single predictor while fixing all other predictors (at their means or reference levels), but we can use the at option to select various levels of another predictor at which to make these plots. So, we will plot predicted loss across a range of hours at selected values of effort:
proc plm source=contcont; effectplot fit (x=hours) / at(effort = 24.52 29.66 34.8); run;
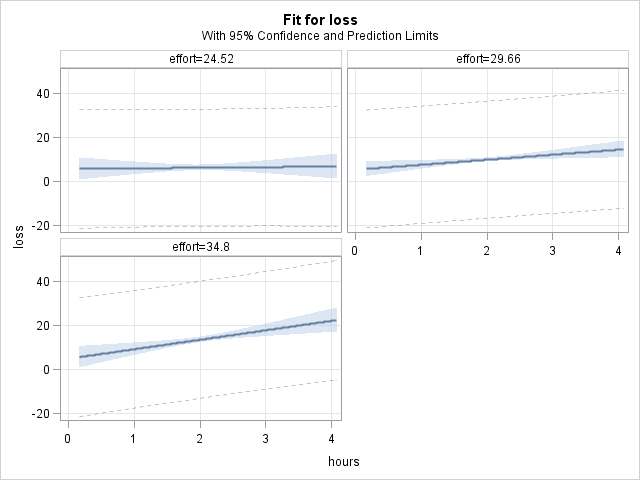
Unfortunately, the lines are not overlaid on the same plot, as we would normally. Furthermore, there is no way to get such a line plot with all 3 lines out of the effectplot statement in proc plm. However, we can still rather easily create this overlaid plot in 3 steps:
-
-
- Create a dataset using a
datastep that contains the range of values of predictors at which we want to estimate the outcome and subsequently plot. - Estimate the outcome at each set of predictor values using the
scorestatement withinproc plm. - Plot the predictor and outcome values, as well as confidence intervals, using the
seriesandbandstatements within proc sgplot.
- Create a dataset using a
-
We first create a dataset of values of the predictors at which we would like to evaluate our outcome. The range of hours in our data is approximately 0 to 4, and we would like to visualize the slope of hours at effort levels 24.52, 29.66, and 34.8. We use do loops to populate the dataset with many values of hours, in increments of 0.1, at each level of effort. For readers uncomfortable with do we provide commented code that achieves a similar dataset for scoring, but with far fewer values of hours between the range of 0 to 4, which will make the confidence intervals appear coarser. We encourage the reader to use do loops to create datasets, as manual entry can be quite laborious if a large range of values is needed. Below we create a dataset called “scoredata” for scoring.
data scoredata; do effort = 24.52, 29.66, 34.8; do hours = 0 to 4 by 0.1; output; end; end; run; /* data scoredata; input effort hours; datalines; 24.52 0 24.52 1 24.52 2 24.52 3 24.52 4 29.66 0 29.66 1 29.66 2 29.66 3 29.66 4 34.8 0 34.8 1 34.8 2 34.8 3 34.8 4 ; run; */
Next, we use the score statement within proc plm to estimate the outcome at each set of effort and hours values.
proc plm source=contcont; score data=scoredata out=plotdata predicted=pred lclm=lower uclm=upper; run;
Note in the code above:
-
-
- We specify the input dataset “scoredata” on the
data=option; the input dataset must contain values for all predictors in the model. - We specify an output dataset “plotdata” on the
out=option; the output dataset contains the predictor and estimated outcome and confidence interval values. - We specify the name of the variables that will hold the estimated outcome, lower confidence limit, and upper confidence limit values, on the
predicted=,lclm=, and the uclm= options, respectively. We use the names “pred”, “lower”, and “upper”.
- We specify the input dataset “scoredata” on the
-
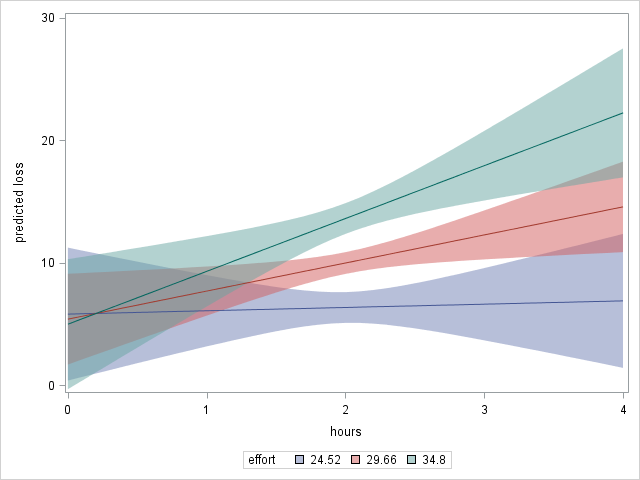
Finally, we use proc sgplot to plot our simple slopes with confidence bands:
proc sgplot data=plotdata; band x=hours upper=upper lower=lower / group=effort transparency=0.5; series x=hours y=pred / group=effort; yaxis label="predicted loss"; run;
Notice in the code above:
- The name of the scored dataset (the output from proc plm) “plotdata”, is specified on the
data=option. - We request a
bandplot for the confidence interval bands. We specify hours on the x-axis, and our variables “upper” and “lower” as the upper and lower limits of the band. We use thegroup=option to request separate bands by effort level, and settransparency=0.5to make the bands somewhat transparent. We plot thebandfirst so that the followingseriesplot will be overlaid on top. - We use the
seriesto plot hours versus the predicted outcome by level of effort (specified ongroup=again), which are our simple slopes. - We rename the y-axis so that we remember what is plotted
The resulting plot:
3 Linear regression, quadratic effect
3.1 Linear regression, quadratic effect: the model
A special case of an interaction of two continuous variables is an interaction of a continuous variable with itself. Interactions are products of variables, so an interaction of a variable with itself is formed by squaring that variable. The squared term is known as the quadratic term. In the same way that the interaction of 2 different continuous variables allows the effect of one of those continuous variables to vary with the level of the other, the interaction of a variable with itself allows its effect to vary with its own level. More specifically, the addition of a quadratic effect to a model allows the linear effect (slope) of that variable to change as the variable changes. In other words, the independent variable and the moderator are the same.
The regression equation with a quadratic effect is straightforward:
\begin{align} Y’ &= \beta_0 \\ &+ \beta_xX \\ &+ \beta_{xx}X*X \end{align}
We interpret the coefficients of the model as:
- \(\beta_0\): intercept, estimate of \(Y’\) when \(X=0\)
- \(\beta_x\): simple slope of \(X\) when \(X=0\)
- \(\beta_{xx}\): 1/2 the change in slope of \(X\) when \(X\) increases by 1-unit (see below)
When we interact two different variables, say \(X\) and \(Z\), the interaction term \(X*Z\) is interpreted as the change in the effect of \(X\) per unit-increase in \(Z\). However, when a variable is interacted with itself, like \(X*X\) above, this interaction term is interpreted as half of the change in the slope of \(X\) per unit-increase in \(X\). We see this when we take the partial derivative of \(Y’\) with respect to \(X\) again to get the formula for the simple slopes of \(X\) in the presence of the quadratic term \(X*X\):
$$Y’ = \beta_0 + \beta_{x}X + \beta_{xx}X^2$$
$$\dfrac{\partial Y’}{\partial X}=slope_{X} = \beta_{x} + 2\beta_{xx}X$$
We can see from this formula that the simple slope of \(X\) changes by \((2\beta_{xx})\) per unit-increase in \(X\).
3.2 Linear regression, quadratic effect: example model
In the following code, we model the linear and quadratic effects of hours on loss. Notice we use the “|” interaction specification to request both the linear and quadratic effects of loss. We also create an item store called “quad” to store the model. A very nice looking plot of the quadratic effect is produced by this code, but only because the model contains no other predictors.
proc glm data=exercise order=internal; model loss = hours|hours / solution; store quad; run;
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| Intercept | -4.12865054 | 5.06766435 | -0.81 | 0.4155 |
| hours | 12.16068708 | 5.01410434 | 2.43 | 0.0155 |
| hours*hours | -2.39805259 | 1.21843555 | -1.97 | 0.0494 |
From this we can construct our regression equation:
$$loss’ = -4.13 + 12.16hours – 2.4hours*hours$$
3.3 Linear regression, quadratic effect: calculating simple slopes and testing them for significance
Let us get the formula for the simple slope of hours in the presence of a quadratic effect of hours:
$$slope_{X} = \beta_{x} + 2\beta_{xx}X$$ $$slope_{hours} = 12.16 – 2*2.4*hours$$
The slope of hours is thus 12.16 when hours = 0, and the slope decreases by (2*2.4=4.8) per unit increase in hours. This suggests that the effect of hours decreases as the number of hours increasing, indicating diminishing returns. Because there are no substantively interesting values of hours, we will estimate the slope of hours when it is at its mean, as well as 1 standard deviation above and below its mean, which are 2, 1.5 and 2.5, respectively.
We will again use estimate statements to calcualte the simple slopes of hours. We can rearrange the terms in the simple slope formula so that the values that we apply to the coefficients appear in parentheses again: $$slope_{hours} = 12.16*(1) – 2.4*(2*hours)$$
Notice that we apply a value of (1) to the linear hours coefficient, and (2*hours) to the quadratic hours coefficient. As a general rule, to calculate the slope of a predictor in the presence of a quadratic effect of that predictor, multiply the linear term for the linear effect by 1, and the quadratic effect by 2 times the value of the predictor at which you would like to evalulate the slope.
proc plm restore=quad;
estimate 'hours slope, hours=mean-sd(1.5)' hours 1 hours*hours 3,
'hours slope, hours=mean(2)' hours 1 hours*hours 4,
'hours slope, hours=mean+sd(2.5)' hours 1 hours*hours 5 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| hours slope, hours=mean-sd(1.5) | 4.9665 | 1.5828 | 897 | 3.14 | 0.0018 |
| hours slope, hours=mean(2) | 2.5685 | 0.9477 | 897 | 2.71 | 0.0069 |
| hours slope, hours=mean+sd(2.5) | 0.1704 | 1.5034 | 897 | 0.11 | 0.9098 |
We see the expected result that as hours increases, its slope decreases.
3.4 Linear regression, quadratic effect: comparing slopes
There is again no need to compare simple slopes in the presence of a quadratic effect (see section 2.5), as it is a continuous by continuous interaction. No matter how far apart or how close we pick values of hours, the simple slopes of hours will always be different from each other, no matter close or far apart we choose our hour values at which to evaluate these slopes.
3.5 Linear regression, quadratic: graphing simple slopes
We can get a graph of the slope of hours as hours changes with the fit type of graph in the effectplot statement within proc plm:
proc plm source=quad; effectplot fit (x=hours); run;
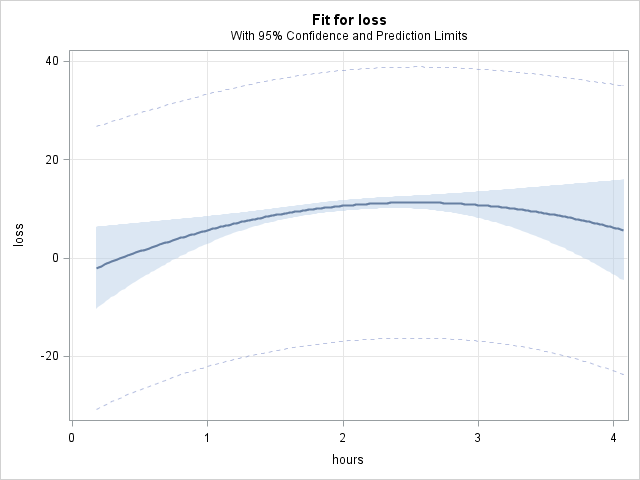 In the graph, the diminishing returns on weight loss by increasing the number of hours is apparent.
In the graph, the diminishing returns on weight loss by increasing the number of hours is apparent.
4. Linear regression, categorical-by-continuous interaction
4.1 Linear regression, categorical-by-continuous interaction: the model
In this section, we model the interaction of a continuous IV and a categorical MV, and then estimate the simple slope of the continuous variable within each category of the MV. We can also think of the continuous variable as the MV and the categorical variable as the IV (the regression model does not distinguish), and then estimate the simple effects of the categorical variable at different levels of the continuous variables. In regression models, categorical variables are typically entered one or more dummy (indicator variables). We discuss this process of recoding categorical variables as dummy variables first.
4.1.1 Categorical predictors and dummy variables
A categorical predictor with \(k\) categories can be represented by \(k\) dummy (0/1) variables, where the value \(1\) on a dummy signifies membership to that category and \(0\) signifies non-membership. However, one dummy variable is typically omitted from the regression, because predictors that are linear combinations of other predictors are perfectly collinear (provide redundant information), and coefficients for these collinear predictors cannot be estimated. For example, assume we have a 3 category moderating variable, \(M\). Although we could create 3 dummies for representing the 3 categories of \(M\), only two of the dummies can be entered into the regression since one dummy can be generated through a linear combination of the other 2: $$dummy3 = (1-dummy1) + (1-dummy2) – 1$$
The omitted category is known as the reference category. In SAS, by default the last category is chosen as the reference. The table below shows how three dummy variables are created from a 3-category MV, \(M\), although one will be omitted from the regression.
| Original Variable | Dummy Variable | Dummy Variable | Omitted Dummy | |
|---|---|---|---|---|
| M | M=1 | M=2 | M=3 | |
| 1 | 1 | 0 | 0 | |
| 2 | 0 | 1 | 0 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 0 | 1 |
In the remainder of the seminar, we will use names such as \(M=1\) and \(M=2\) to denote categories indiciated by dummy variables.
Interacting a continuous predictor with a categorical predictor is achieved by multiplying the continuous variable by each of the dummy variables, although once again, the interaction variable formed with the omitted dummy will also be omitted:
| Continuous Variable | Dummy Variable | Dummy Variable | Interaction Variable | Interaction Variable | Omitted Dummy | Omitted Interaction | |
|---|---|---|---|---|---|---|---|
| X | M=1 | M=2 | X*M=1 | X*M=2 | M=3 | X*M=3 | |
| 10 | 1 | 0 | 10 | 0 | 0 | 0 | |
| 17 | 0 | 1 | 0 | 17 | 0 | 0 | |
| 23 | 0 | 1 | 0 | 23 | 0 | 0 | |
| 12 | 0 | 0 | 0 | 0 | 1 | 12 |
The regression equation for a continuous IV, \(X\), interacted with a 3-category MV, \(M\), is: \begin{align} Y’ &= \beta_0 \\ &+ \beta_{x}X \\ &+ \beta_{m1}(M=1) + \beta_{m2}(M=2) \\ &+ \beta_{xm1}X*(M=1) + \beta_{xm2}X*(M=2) \end{align}
Notice how neither of the omitted variables, \(M=3\) and \(X*M=3\), appear in the regression equation. The coefficients above have the following interpretation:
- \(\beta_0\): intercept, estimate of \(Y’\) when \(X=0\) and \(M=3\); that is, the estimate of the outcome when all predictors, dummies included, are equal to 0
- \(\beta_x\): simple slope of \(X\) when \(M=3\), the slope in the reference category
- \(\beta_{m1}\): simple effect of \(M=1\) vs \(M=3\) when \(X=0\)
- \(\beta_{m2}\): simple effect of \(M=2\) vs \(M=3\) when \(X=0\)
- \(\beta_{xm1}\): difference in slope of \(X\) when \(M=1\) vs \(M=3\), or difference in effect of \(M=1\) vs \(M=3\) for each additional unit-increase in \(X\)
- \(\beta_{xm2}\): difference in slope of \(X\) when \(M=2\) vs \(M=3\), or difference in effect of \(M=2\) vs \(M=3\) for each additional unit-increase in \(X\)
Once again that the individual terms, \(\beta_x\), \(\beta_{m1}\), and \(\beta_{m1}\) represent simple slopes and effects at the reference level of the interacting variable, and that the interaction terms, \(\beta_{xm1}\) and \(\beta_{xm1}\), represent changes in simple slopes and effects.
Taking partial derivatives with respect to \(X\) will give us the formula for simple slopes: $$\dfrac{\partial Y’}{\partial X} = \beta_{x} + \beta_{xm1}(M=1) + \beta_{xm2}(M=2)$$ $$slope_{X} = \beta_{x} + \beta_{xm1}(M=1) + \beta_{xm2}(M=2)$$
We can construct a formula for the simple slope of \(X\) for each category of \(M\) by substituting in ones and zeroes into the slope equation: \begin{align} slope_{X|M=1} &= \beta_{x} + \beta_{xm1} \\ slope_{X|M=2} &= \beta_{x} + \beta_{xm2} \\ slope_{X|M=3} &= \beta_{x} \end{align}
Although we could analyze the simple effects of \(M\) at various levels of \(X\), we postpone the estimation of simple effects until section 5.
IMPORTANT: SAS parameterization of categorical (class) predictors
In most SAS procedures, when categorical variables are specified on the class statement, SAS automatically creates dummy (0/1) variables for each level of the variable, and enters all dummies (not all but one) into the regression equation, creating a reference group represented by this omitted dummy (by default, the last group sorted by formatted values). To ensure this is the parameterization, for most procedures, the option param=glm can be added to the class statement.
When an interaction of two or more categorical variable is entered in the model, more than one dummy may be omitted (see below in the categorical-by-categorical interaction section). The coefficients for these omitted dummies are not technically estimated but are constrained to be equal to 0, which achieves the same result as omission. These 0 coefficients will appear in the output regression table and may need to be referenced in estimate statements used to calculate simple effects (to avoid this confusion, this seminar does not use estimate statements to estimate simple effects, but the slice and lsmestimate statements instead). Thus, the above regression equation in SAS would include 0 coefficients for all of the omitted variables, \((M=3)\) and \((X*M=3)\), which we have identified below with a \(0\) symbol rather than a \(\beta\). These zeroed coefficients will appear in the output regression table:
\begin{align} Y’&= \beta_0 + \beta_{x}X \\ &+ \beta_{m1}(M=1) + \beta_{m2}(M=2) + 0_{m3}(M=3) \\ &+ \beta_{xm1}X*(M=1) + \beta_{xm2}X*(M=2) + 0_{xm3}X*(M=3) \end{align}
4.2 Linear regression, categorical-by-continuous interaction: example model
Let us begin our analysis of simple slopes and simple effects in a model with a categorical by continuous interaction. In the following model, we will predict loss by prog (categorical), hours (continuous), and their interaction. Following model fitting, we might be interested in the simple slopes of hours within each category of prog and the simple effects of progs at different levels of hours. We use proc glm to first estimate this model.
proc glm data=exercise order=internal; class prog; model loss = prog|hours / solution; store catcont; run;
Notice in the code above:
class prog: declares progrm to be a categorical variable. SAS will create 0/1 dummy variables for each category of prog, and will enter all of them into the regression (see section IMPORTANT: SAS parameterization of categorical (class) predictors).order=internal: When formats are applied to a variable, SAS will by default reorder the levels of the variable in the alphabetic order of the formats. Above, we applied the following formats to prog: 1 = jogging, 2 = reading, and 3 = swimming. Without further instruction, SAS will make jogging the first level, reading the second, and swimming the third. We find this confusing (and we want to compare to the 2 exercise progs to reading), so we tell SAS to use the original numbering as the ordering with the optionorder=internal
The output of the model is below:
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| hours | 1 | 3116.205464 | 3116.205464 | 73.71 | <.0001 |
| prog | 2 | 2901.898322 | 1450.949161 | 34.32 | <.0001 |
| hours*prog | 2 | 5319.048143 | 2659.524072 | 62.91 | <.0001 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| | |
|---|---|---|---|---|---|
| Intercept | 2.21637209 | B | 1.48612022 | 1.49 | 0.1362 |
| hours | -2.95616163 | B | 0.70795538 | -4.18 | <.0001 |
| prog jogging | -8.99703193 | B | 2.21602813 | -4.06 | <.0001 |
| prog swimming | 9.93260912 | B | 2.17711476 | 4.56 | <.0001 |
| prog reading | 0.00000000 | B | . | . | . |
| hours*prog jogging | 10.40891093 | B | 1.07225125 | 9.71 | <.0001 |
| hours*prog swimming | 9.83021575 | B | 1.05144861 | 9.35 | <.0001 |
| hours*prog reading | 0.00000000 | B | . | . | . |
We include the Type III SS output table because it contains an overall test of the interaction of hours and prog. This is a joint test of the two interaction coefficients, \(\beta_{xm1}\) and \(\beta_{xm2}\), against 0. A significant test usually indicates at least one of the interaction coefficients is not equal to zero. We see that our interaction of hours and prog is significant (p<0.001), which allows us to analyze the interaction more deeply.
The regression table gives us all the coefficients we need to construct the regression equation:
\begin{align} loss’&= 2.22 \\ &- 2.96hours \\ &-9.0(prog=1) + 9.93(prog=2) + 0(prog=3) \\ &+ 10.41hours*(prog=1) + 9.83hours*(prog=2) + 0hours*(prog=3) \end{align}
Using the equations for the slopes above, we can manually calculate what the simple slopes should be:
\begin{align} slope_{prog1}& = -2.96 + 10.41 = 7.45 \\ slope_{prog2}& = -2.96 + 9.83 = 6.87 \\ slope_{prog3}& = -2.96 + 0 = -2.96 \end{align}
We next use the estimate statement in proc plm to calculate these slopes and test them for significance against 0.
4.3 Linear regression, categorical by continuous interaction: calculating simple slopes and testing them for significance
Below are the formulas or our simple slopes of read within each category of prog with the values that we will apply to each coefficient for the estimate statement in parentheses:
\begin{align}
slope_{m1}& = \beta_{x}(1) + \beta_{xm1}(1) \\
slope_{m2}& = \beta_{x}(1) + \beta_{xm2}(1) \\
slope_{m3}& = \beta_{x}(1) + \beta_{xm3}(1)
\end{align}
Even though the coefficient for \(\beta_{xm3}\) is constrained to 0 by SAS, we still must apply a value of 1 to it in the estimate statement (see below Potential Pitfall). Here are the estimate statements for these simples slopes and the corresponding output.
proc plm restore = catcont;
estimate 'hours slope, prog=1 jogging' hours 1 hours*prog 1 0 0,
'hours slope, prog=2 swimming' hours 1 hours*prog 0 1 0,
'hours slope, prog=3 reading' hours 1 hours*prog 0 0 1 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| hours slope, prog=1 jogging | 7.4527 | 0.8053 | 894 | 9.25 | <.0001 |
| hours slope, prog=2 swimming | 6.8741 | 0.7774 | 894 | 8.84 | <.0001 |
| hours slope, prog=3 reading | -2.9562 | 0.7080 | 894 | -4.18 | <.0001 |
In the output, notice:
- The estimated slopes match our manual calculations.
- The slope of hours is significant in all 3 categories of prog, though negative for prog=3, the reading group, suggesting that increasing the number of weekly hours in the jogging and reading programs predict greater weight loss, and less weight loss in the reading program.
- The slope estimate within prog=3 is the same estimate as the
hoursparameter in the regression table. Again, when effects are interacted with other effects, do not interpret individual terms as main effects. They are simple effects within the reference group. This also implies that one does not need to useestimatestatements to calculate the simple slope in the reference group: it is already estimated in the regression itself
Potential Pitfall: Although we just mentioned that we do not need to use estimate statements to calculate the simple slope in the reference group, we demonstrated how in order to point out a pitfall in using estimate statements. It would seem that one could specify the simple slope of hours in the reference group prog=3 just by supplying a value for the hours coefficient, and not for the interaction of hours and prog=3, since it is constrained to 0:
proc plm restore = catcont; estimate 'hours slope, prog=3 reading (wrong)' hours 1 / e; run;
After all, the simple slope for prog=3 is just the coefficient for hours. However, in SAS, if an effect is part of an interaction, and the coefficients and values for that interaction are omitted from the estimate statement, then balanced (equal) values are applied to the interaction coefficients, producing a slope averaged across all categories rather than a single slope within one category.
This is a case where the e option is important. The e option produces a table of values that SAS applies to each coefficient in the model. We can see that SAS did NOT apply values of 0 to the interaction coefficients as we hoped it would:
| Estimate Coefficients | ||
|---|---|---|
| Effect | prog | Row1 |
| Intercept | ||
| prog | jogging | |
| prog | swimming | |
| prog | reading | |
| hours | 1 | |
| hours*prog | jogging | 0.3333 |
| hours*prog | swimming | 0.3333 |
| hours*prog | reading | 0.3333 |
Instead, SAS applies values of 0.33333 to each interaction coefficient (a value of 1 distributed evenly across 3 categories). This will estimate the unweighted average of the 3 simple slopes \((7.45+6.87-2.96)/3 = 3.79v\):
| Estimate | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| hours slope, prog=3 reading (wrong) | 3.7902 | 0.4415 | 894 | 8.59 | <.0001 |
Use of the e can prevent this type of unintended specifcation.
4.4 Linear regression, categorical by continuous interaction: comparing simple slopes
We also want to know if the simple slopes are significantly different from each, which we can test by comparing differences between slopes against zero.
Once again, estimating the difference between these simple slopes is achieved by taking the difference between values corresponding to each slope’s set of coefficients. Recall the estimate statement used to calculate each simple slope:
estimate 'hours slope, prog=1 jogging' hours 1 hours*prog 1 0 0,
'hours slope, prog=2 swimming' hours 1 hours*prog 0 1 0,
'hours slope, prog=3 reading' hours 1 hours*prog 0 0 1
We simply subtract one set of values across all coefficients for one slope from the set of values for another slope to get the difference. Here is the code and output for the 3 differences between these 3 slopes. Notice that because the value for hours cancels to 0 for all 3 estimated differences, we can drop the read coefficient.
proc plm restore = catcont;
estimate 'diff slopes, prog=1 vs prog=2' hours*prog -1 1 0,
'diff slopes, prog=1 vs prog=3' hours*prog -1 0 1,
'diff slopes, prog=2 vs prog=3' hours*prog 0 -1 1 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| diff slopes, prog=1 vs prog=2 | -0.5787 | 1.1193 | 894 | -0.52 | 0.6053 |
| diff slopes, prog=1 vs prog=3 | -10.4089 | 1.0723 | 894 | -9.71 | <.0001 |
| diff slopes, prog=2 vs prog=3 | -9.8302 | 1.0514 | 894 | -9.35 | <.0001 |
Notice:
- The 2 slopes in prog=1 and prog=2 are not significantly different from one another, p=.6053.
- The latter 2 esimates, prog=1 vs prog=3 and prog=2 vs prog=3, are just the interaction coefficients from the regression table. So, the only unknown comparison was the first.
4.5 Linear regression, categorical by continuous interaction: graphing simple slopes
Graphing the simple slopes of hours within each category of prog is simple with a slicefit graph in the effectplot statement of proc plm. A slicefit graph is used to plot the outcome across a range of continuous variables at discrete levels of another variable (typically a categorical variable):
proc plm resore=catcont; effectplot slicefit (x=hours sliceby=prog) / clm; run;
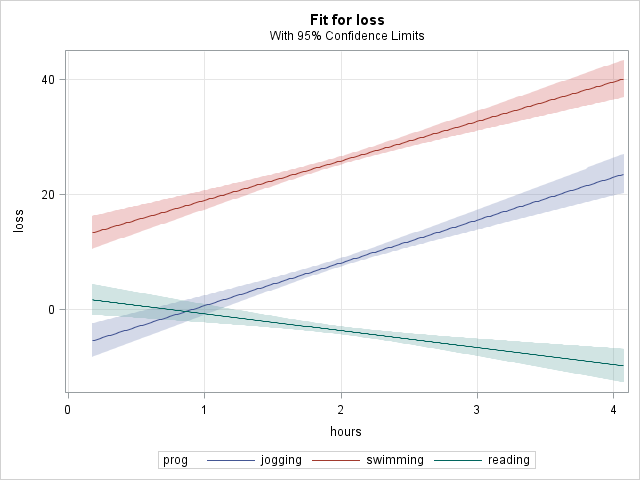
In the code above, notice:
- In the
effectplotstatement, we specify that hours is to appear on the x-axis, with separate lines “sliced” by prog. Since prog is categorical, SAS will plot separate lines of hours vs the predicted outcome at each level of prog. Had we specified a continuous variable on theslicebyoption, SAS would have picked 5 evenly spaced values across the range of the variable at which to plot the lines. - We request confidence limits on the simple slopes using the
clmoption on theeffectplotstatement. Unlike in afitplot, confidence bands are not produced by default in aslicefitgraph.
In the graph it is easy to see that the simple slopes of hours did not differ between the jogging and swimming programs and that these 2 slopes differed from the slope in the reading program.
NOTE: It is also common to estimate the simple effects of a categorical variable at different levels of a continuous variable, but we introduce the analysis of simple effects in the next section.
5. Linear regression, categorical-by-categorical interaction
5. Linear regression, categorical-by-categorical interaction: the model
When modeling the interaction of two categorical variables, we will usually conduct an analysis of the simple effects of one or both of the categorical variables across levels of the other. We first examine a regression equation with such an interaction. Let us look at a simple examples where we enter a 2-level categorical IV, \(X\), which takes on the values (0,1) a 3-level categorical MV, \(M\), which takes on the values (1,2,3), and their interaction \(X*M\), which takes on 6 pairs of values [(0,1), (0,2), (0,3), (1,1), (1,2), (1,3)].
5.1.1 Interactions of categorical predictors as dummy variables
As discussed above, a categorical predictor with \(k\) categories can be represented by \(k\) dummy (0/1) variables, though one is usually omitted from the regression. Thus we need 1 dummy for \(X\) and 2 for \(M\). In SAS, by default the last category is chosen as the reference, so our two reference categories are \(X=1\) and \(M=3\).
| Original Variable | Dummy Variable | Omitted Dummy | ||
|---|---|---|---|---|
| X | X=0 | X=1 | ||
| 0 | 1 | 0 | ||
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | ||
| 1 | 0 | 1 |
| Original Variable | Dummy Variable | Dummy Variable | Omitted Dummy | ||
|---|---|---|---|---|---|
| M | M=1 | M=2 | M=3 | ||
| 1 | 1 | 0 | 0 | ||
| 2 | 0 | 1 | 0 | ||
| 2 | 0 | 1 | 0 | ||
| 3 | 0 | 0 | 1 |
An interaction variable is formed as the product of 2 variables. For the interaction of 2 categorical variables, we simply multiply the dummies across the 2 variables to form \(2\times3=6\) interaction dummy variables. However, any interaction dummy formed by any omitted dummy for \(X\) or \(M\) (\(X=1\) or \(M=3\)) will also be omitted from the regression because of collinearity:
| Original Variable | Original Variable | Dummy Variable | Dummy Variable | Dummy Variable | Interaction Dummy | Interaction Dummy | Omitted Dummy | Omitted Dummy | Omitted Interaction | Omitted Interaction | Omitted Interaction | Omitted Interaction | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | M | X=0 | M=1 | M=2 | X=0,M=1 | X=0,M=2 | X=1 | M=3 | X=0,M=3 | X=1,M=1 | X=1,M=2 | X=1,M=3 | ||
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 2 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | ||
| 1 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
Let’s now look at a regression equation where we are trying to predict a DV, \(Y\), with \(X\), \(M\), and their interaction.
\begin{align} Y’ &= \beta_0 \\ &+ \beta_{x0}(X=0) \\ &+ \beta_{m1}(M=1) + \beta_{m2}(M=2) \\ &+ \beta_{x0m1}(X=0,M=1) + \beta_{x0m2}(X=0,M=2) \end{align}
As explained above, we have omitted from the regression equation two dummy variables representing the reference groups in \(X\), \(X=1\), and \(M\), \(M=3\) as well 4 interaction dummies representing \((X=0,M=3)\), \((X=1,M=1)\), \((X=1,M=2)\), and \((X=1,M=3)\). The interpretation each of the coefficients in the regression equation above:
- \(\beta_0\): the expected value of \(Y’\) when \(X=1\) and \(M=3\)
- \(\beta_{x0}\): the effect of \(X=0\) vs \(X=1\) when \(M=3\)
- \(\beta_{m1}\): the effect of \(M=1\) vs \(M=3\) when \(X=1\)
- \(\beta_{m2}\): the effect of \(M=2\) vs \(M=3\) when \(X=1\)
- \(\beta_{x0m1}\): the additional effect of \(X=0\) vs \(X=1\) when \(M=1\), as compared to when \(M=3\); or the additional effect of \(M=1\) vs \(M=3\) when \(X=0\), as compared to when \(X=1\)
- \(\beta_{x0m2}\): the additional effect of \(X=0\) vs \(X=1\) when \(M=2\), as compared to when \(M=3\); or the additional effect of \(M=2\) vs \(M=3\) when \(X=0\), as compared to when \(X=1\)
Remember that in SAS, although the coefficients for dummy variables involving reference groups are not technically estimated and constrained to 0, they are nevertheless part of the model and are included when calculating the means of reference groups. We thus can expand our regression equation to reflect these additional coefficients, which have the symbol \(\beta\) replace with a \(0\) :
$$ \begin{align} Y’ &= \beta_0 \\ &+ \beta_{x0}(X=0) + 0_{x1}(X=1) \\ &+ \beta_{m1}(M=1) + \beta_{m2}(M=2) + 0_{m2}(M=3) \\ &+ \beta_{x0m1}(X=0,M=1) + \beta_{x0m2}(X=0,M=2) + 0_{x0m3}(X=0,M=3) \\ &+ 0_{x1m1}(X=1,M=1) + 0_{x1m2}(X=1,M=2) + 0_{x1m3}(X=1,M=3) \end{align} $$
We next derive formulas for our simple effects. We previously used partial derivatives to derive the formulas for our simple slopes, but simple effects describe discrete changes (from 0 to 1) whereas derivatives are defined only for continuous functions. Instead we should think of simple effects as differences in means, and this framework will aid in our coding for the lsmestimate statement. Let’s begin with the simple effect of \(X\) within each level of \(M\).
The simple effect of \(X\) at \(M=1\) is the difference between the expected mean outcome \(Y’\) when \(X=0,M=1\) and \(X=1,M=1\). We can thus express the simple effect like so (where \(\mu_{x,m}\) is the expected mean \(Y’\) when \(X=x\) and \(M=m\)): $$effect_{x|m=1} = \mu_{0,1} – \mu_{1,1}$$
We can express all of our simple effects as differences between means. $$effect_{x|m=1} = \mu_{0,1} – \mu_{1,1}$$ $$effect_{x|m=2} = \mu_{0,2} – \mu_{1,2}$$ $$effect_{x|m=3} = \mu_{0,3} – \mu_{1,3}$$ $$effect_{m=1-m=2|x=0} = \mu_{0,1} – \mu_{0,2}$$ $$effect_{m=1-m=3|x=0} = \mu_{0,1} – \mu_{0,3}$$ $$effect_{m=2-m=3|x=0} = \mu_{0,2} – \mu_{0,3}$$ $$effect_{m=1-m=2|x=1} = \mu_{1,1} – \mu_{1,2}$$ $$effect_{m=1-m=3|x=1} = \mu_{1,1} – \mu_{1,3}$$ $$effect_{m=2-m=3|x=1} = \mu_{1,2} – \mu_{1,3}$$
5.2 Linear regression, categorical by categorical interaction: example model
We demonstrate the analysis of a categorical-by-cateogrical interaction with the regression of loss on program, female, and their interaction:
proc glm data=exercise order=internal; class prog female; model loss = female|prog / solution e; store catcat; run;
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| female | 1 | 7.6337 | 7.6337 | 0.18 | 0.6718 |
| prog | 2 | 133277.2061 | 66638.6031 | 1568.25 | <.0001 |
| prog*female | 2 | 7463.1979 | 3731.5990 | 87.82 | <.0001 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| | |
|---|---|---|---|---|---|
| Intercept | -3.62014949 | B | 0.53224276 | -6.80 | <.0001 |
| female male | -0.33545693 | B | 0.75270492 | -0.45 | 0.6559 |
| female female | 0.00000000 | B | . | . | . |
| prog jogging | 7.90883093 | B | 0.75270492 | 10.51 | <.0001 |
| prog swimming | 32.73784051 | B | 0.75270492 | 43.49 | <.0001 |
| prog reading | 0.00000000 | B | . | . | . |
| prog*female jogging male | 7.81880323 | B | 1.06448551 | 7.35 | <.0001 |
| prog*female jogging female | 0.00000000 | B | . | . | . |
| prog*female swimming male | -6.25985085 | B | 1.06448551 | -5.88 | <.0001 |
| prog*female swimming female | 0.00000000 | B | . | . | . |
| prog*female reading male | 0.00000000 | B | . | . | . |
| prog*female reading female | 0.00000000 | B | . | . | . |
We see that the interaction of prog and female is significant. Let’s construct a regression equation for loss (omitting the 0 coefficients for visual clarity):
\begin{align} loss’ &= -3.62 \\ &- .34(female=0) \\ &+ 7.91(prog=1) + 32.74(prog=2) \\ &+ 7.82(female=0,prog=1) – 6.26(female=0,prog=2) \end{align}
We will use 2 different statements to calculate the simple effects of being male within each program, the slicestatement and the lsmestimate statement, which we visit a little later.
5.3 Linear regression, categorical-by-categorical interaction: estimating simple effects with the slice statement
The slice statement is specifically used to analyze the effects of categorical variables nested in higher-order effects (interactions) composed entirely of categorical variables, which are simple effects. The slice statement provides the simplest syntax for the analysis of simple effects:
slice interaction_effect / sliceby= diff
- interaction_effect: specification of the interaction to be decomposed for simple effects analysis — only
classvariables are allowed in this interaction - sliceby=: specifies the variable in the interaction_effect at whose distinct levels the simple effect of the interacting variable(s) will be calculated
- diff: optional, but strongly recommended as it provides an estimate of the simple effect (not just a test of its significance)
Below we use the slice statement to analyze simple effects two ways: first the simple effect of gender(female) within each program (prog), and then the simple effects of program within each gender. Notice: :
- A Bonferroni adjustment to the p-values for the tests of significance is requested with the option
adj=bonbecause of the numerous comparsions. The Bonferroni adjustement is applied to each set of comparisons within a distinct level of thesliceby=variable. Other adjustment methods are available. - The option
plots=nonesuppresses the default plots created by theslicestatement, which are difficult for most users to interpret. Thenofoptionto suppresses the default F-test used to test the simple effects, as it is mostly redundant with the t-test provided by thediffoption. - Although not displayed below, we also request that the means of each cell in the interactino be printed with the
meansoption.
proc plm restore = catcat; slice female*prog / sliceby=prog diff adj=bon plots=none nof e means; slice female*prog / sliceby=female diff adj=bon plots=none nof e means; run;
| Simple Differences of prog*female Least Squares Means Adjustment for Multiple Comparisons: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slice | female | _female | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| prog jogging | male | female | 7.4833 | 0.7527 | 894 | 9.94 | <.0001 | <.0001 |
| Simple Differences of prog*female Least Squares Means Adjustment for Multiple Comparisons: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slice | female | _female | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| prog swimming | male | female | -6.5953 | 0.7527 | 894 | -8.76 | <.0001 | <.0001 |
| Simple Differences of prog*female Least Squares Means Adjustment for Multiple Comparisons: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slice | female | _female | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| prog reading | male | female | -0.3355 | 0.7527 | 894 | -0.45 | 0.6559 | 0.6559 |
| Simple Differences of prog*female Least Squares Means Adjustment for Multiple Comparisons: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slice | prog | _prog | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female male | jogging | swimming | -10.7504 | 0.7527 | 894 | -14.28 | <.0001 | <.0001 |
| female male | jogging | reading | 15.7276 | 0.7527 | 894 | 20.89 | <.0001 | <.0001 |
| female male | swimming | reading | 26.4780 | 0.7527 | 894 | 35.18 | <.0001 | <.0001 |
| Simple Differences of prog*female Least Squares Means Adjustment for Multiple Comparisons: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Slice | prog | _prog | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female female | jogging | swimming | -24.8290 | 0.7527 | 894 | -32.99 | <.0001 | <.0001 |
| female female | jogging | reading | 7.9088 | 0.7527 | 894 | 10.51 | <.0001 | <.0001 |
| female female | swimming | reading | 32.7378 | 0.7527 | 894 | 43.49 | <.0001 | <.0001 |
Each of the output tables above comprises the analysis of simple effects within one level of the sliceby= variable. The first 3 tables are the simple effect of female within each level of prog, while the latter two tables are the simple effect of prog within each level of female. In the first 3 tables, we see that there are significant effects of gender within the jogging and swimming programs, but not in the reading program. In the latter 2 tables, we see that all 3 programs differ from one another for both genders, though by quite different amounts between the two genders (for example, jogging vs reading = -10.75 for males wheile jogging vs reading = -24.83 for females).
Note: The slice statement is basically a restricted form of the much more widely known lsmeans statement. The slice statement was designed specifically to analyze simple effects and shares the same options as the lsmeans statement. Although the lsmeans statement can calculate simple effects, it can be more difficult to restrict the estimations to only those simple effects of interest than in a slice statement. The lsmeans statement can more easily compare the groups formed by an interaction to a single “control” group, rather than calculate simple effects nested within an interaction.
We now look at how to estimate our simple effects using the lsmestimate statement. Although the syntax is simpler in the slice statement, facility with the lsmestimate will help with coding more complex custom hypotheses in the future (for example, comparing the simple effect of one group to the average simple effect of severalg groups). We also must use the lsmestimate statement if we are to compare simple effects across groups.
5.4 Linear regression, categorical-by-categorical interaction: estimating simple effects with the lsmestimate statement
The lsmestimate combines the functionality of the lsmeans statement and the estimate statement to test linear combinations (estimate) of least squares means (lsmeans). The minimum coding of the lsmestimate statement for the decomposition of a 2-way interaction is (using nonpositional syntax, see here for a discussion of positional and nonpositional syntax):
lsmestimate effect [value, level_x level_m]…
-
- effect: the interaction to be subjected to simple effect analysis.
- [value, level_x level_m]: specifies at which levels of \(X\) and \(M\) the mean of the outcome is to be estimated, and the value to apply to it in a linear combination. The comma is optional but helps to separate the value from the specification of the mean. IMPORTANT: specify the rank (ordinal, i.e. first, second, third, etc.) level of \(X\) and \(M\), not the actual value. For example, to specify the mean when \(X=1\) and \(M=1\) with a value of 1, we would specify [1, 2 1], because value=1, \(X=1\) is the second level of \(X\), and \(M=1\) is the first level of \(M\).For estimation of a simple effect in an
lsmestimatestatement, we will specify 2 different means, one with a value of 1 and the other with value of -1.
We can directly translate the formulas below into lsmestimatestatements simply by applying a value of 1 to the first mean, a value of -1 to the second mean, and being careful to specify a 1 when \(X=0\) and a 2 when \(X=1\):
$$effect_{x|m=1} = \mu_{0,1} – \mu_{1,1}$$
$$effect_{x|m=2} = \mu_{0,2} – \mu_{1,2}$$
$$effect_{x|m=3} = \mu_{0,3} – \mu_{1,3}$$
$$effect_{m=1-m=2|x=0} = \mu_{0,1} – \mu_{0,2}$$
$$effect_{m=1-m=3|x=0} = \mu_{0,1} – \mu_{0,3}$$
$$effect_{m=2-m=3|x=0} = \mu_{0,2} – \mu_{0,3}$$
$$effect_{m=1-m=2|x=1} = \mu_{1,1} – \mu_{1,2}$$
$$effect_{m=1-m=3|x=1} = \mu_{1,1} – \mu_{1,3}$$
$$effect_{m=2-m=3|x=1} = \mu_{1,2} – \mu_{1,3}$$
Below is the code for the simple effects. We apply a Bonferroni correction again using the adj=bon option:
proc plm restore=catcat; lsmestimate female*prog 'male-female, prog = jogging(1)' [1, 1 1] [-1, 2 1], 'male-female, prog = swimming(2)' [1, 1 2] [-1, 2 2], 'male-female, prog = reading(3)' [1, 1 3] [-1, 2 3], 'jogging-reading, female = male(0)' [1, 1 1] [-1, 1 3], 'jogging-reading, female = female(1)' [1, 2 1] [-1, 2 3], 'swimming-reading, female = male(0)' [1, 1 2] [-1, 1 3], 'swimming-reading, female = female(1)' [1, 2 2] [-1, 2 3], 'jogging-swimming, female = male(0)' [1, 1 1] [-1, 1 2], 'jogging-swimming, female = female(1)' [1, 2 1] [-1, 2 2] / e adj=bon; run;
| Least Squares Means Estimates Adjustment for Multiplicity: Bonferroni | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female*prog | male-female, prog = jogging(1) | 7.4833 | 0.7527 | 894 | 9.94 | <.0001 | <.0001 |
| female*prog | male-female, prog = swimming(2) | -6.5953 | 0.7527 | 894 | -8.76 | <.0001 | <.0001 |
| female*prog | male-female, prog = reading(3) | -0.3355 | 0.7527 | 894 | -0.45 | 0.6559 | 1.0000 |
| female*prog | jogging-reading, female = male(0) | 15.7276 | 0.7527 | 894 | 20.89 | <.0001 | <.0001 |
| female*prog | jogging-reading, female = female(1) | 7.9088 | 0.7527 | 894 | 10.51 | <.0001 | <.0001 |
| female*prog | swimming-reading, female = male(0) | 26.4780 | 0.7527 | 894 | 35.18 | <.0001 | <.0001 |
| female*prog | swimming-reading, female = female(1) | 32.7378 | 0.7527 | 894 | 43.49 | <.0001 | <.0001 |
| female*prog | jogging-swimming, female = male(0) | -10.7504 | 0.7527 | 894 | -14.28 | <.0001 | <.0001 |
| female*prog | jogging-swimming, female = female(1) | -24.8290 | 0.7527 | 894 | -32.99 | <.0001 | <.0001 |
5.5 Linear regression, categorical-by-categorical interaction: comparing simple effects
Although coding the syntax for the estimation of simple effects is a bit more laborious in lsmestimate statements than in slice statements, of the two only lsmestimate statements can compare simple effects. Fortunately, once we have our lsmestimate statement code for calculating simple effects, the ensuing comparisons are very simple to code. To compare simple effects, we simply take the 2 sets of means for each simple effect, and reverse the values in the second set:
$$(\mu_{0,1}-\mu_{1,1})-(\mu_{0,2}-\mu_{1,2}) = \mu_{0,1}-\mu_{1,1}-\mu_{0,2}+\mu_{1,2}$$.
For example, imagine we want to test whether the simple effect of gender in the jogging program is the same as the simple effect of gender in the swimming program. Let’s revisit the lsmestimate statement code to calculate these two simple effects(with some extra spacing to align the values):
lsmestimate female*prog 'male-female, prog = jogging(1)' [1, 1 1] [-1, 2 1], 'male-female, prog = swimming(2)' [1, 1 2] [-1, 2 2], run;
To compare these effects we simply put the second set of means on the same row as the first but reverse the coefficients:
lsmestimate prog*female 'diff male-female, prog=1 - prog=2' [1, 1 1] [-,1 2 1] [-1, 1 2] [1, 2 2];
We can easily extend this to compare the simple effect of gender across programs and the simple effects of programs across genders:
proc plm restore=catcat; lsmestimate prog*female 'diff male-female, prog=1 - prog=2' [1, 1 1] [-1, 2 1] [-1, 1 2] [1, 2 2], 'diff male-female, prog=1 - prog=3' [1, 1 1] [-1, 2 1] [-1, 1 3] [1, 2 3], 'diff male-female, prog=2 - prog=3' [1, 1 2] [-1, 2 2] [-1, 1 3] [1, 2 3], 'diff jogging-reading, male - female' [1, 1 1] [-1, 1 3] [-1, 2 1] [1, 2 3], 'diff swimming-reading, male - female' [1, 1 2] [-1, 1 3] [-1, 2 2] [1, 2 3], 'diff jogging-swimming, male - female' [1, 1 1] [-1, 1 2] [-1, 2 1] [1, 2 2]/ e adj=bon; run;
| Least Squares Means Estimates Adjustment for Multiplicity: Bonferroni | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female*prog | diff male-female, prog=1 – prog=2 | 14.0787 | 1.0645 | 894 | 13.23 | <.0001 | <.0001 |
| female*prog | diff male-female, prog=1 – prog=3 | 7.8188 | 1.0645 | 894 | 7.35 | <.0001 | <.0001 |
| female*prog | diff male-female, prog=2 – prog=3 | -6.2599 | 1.0645 | 894 | -5.88 | <.0001 | <.0001 |
| female*prog | diff jogging-reading, male – female | 7.8188 | 1.0645 | 894 | 7.35 | <.0001 | <.0001 |
| female*prog | diff swimming-reading, male – female | -6.2599 | 1.0645 | 894 | -5.88 | <.0001 | <.0001 |
| female*prog | diff jogging-swimming, male – female | 14.0787 | 1.0645 | 894 | 13.23 | <.0001 | <.0001 |
Notice how the symmetry of the estimates of the differences reflects the symmetry of the interaction. It appears that all of our simple effects are different from one another.
5.6 Linear regression, categorical-by-categorical interaction: graphing simple effects
The effectplot statement once again provides an easy method to graph our simple effects. This time, we will be using an interaction graph, which has virtually identical syntax to a slicefit graph, to plot both sets of our simple effects. We add the connect option because adding confidence limits with the clm opotion removes the lines connecting the means, for some unknown reason. Non-parallel lines provide a quick graphical assessment of an interaction, so we want them:
proc plm restore=catcat; effectplot interaction (x=female sliceby=prog) / clm connect; effectplot interaction (x=prog sliceby=female) / clm connect; run;
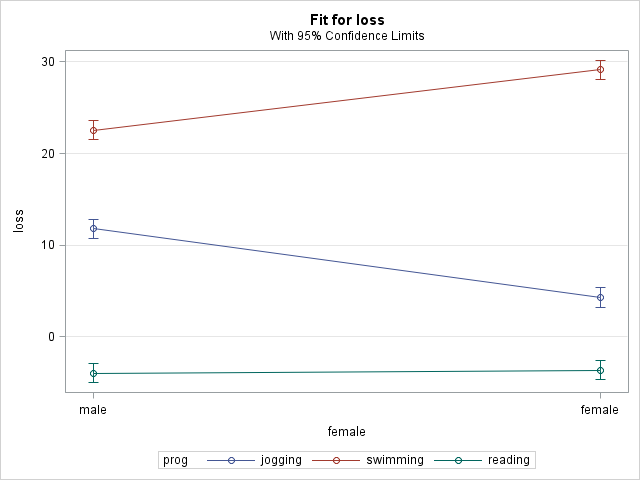
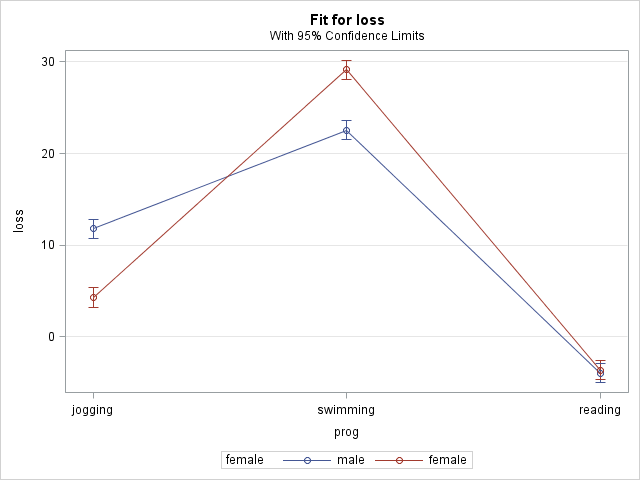
The graphs make the simple effects easier to interpret. In the top graph, we see that the females benefit significantly more from the swimming program (b=-6.5953, p < .001), males significantly benefit more from the jogging program (b=7.4833, p< .001), whereas neither show more benefit in the reading program (b=-0.3355, p=.6559). Each of these effects are significantly differently from each other (all p<.001). In the bottom graph, we see that although the general pattern of benefit from each program is similar between the genders, females tend to show greater differences among the programs. For example, both genders benefit significantly more from swimming than jogging (b=-10.7504, p
6. Linear regression, 3-way categorical-categorical-continuous interaction
6.1 Linear regression, 3-way categorical-categorical-continuous interaction: the model
The interaction of 3 variables can be decomposed in quite a few more ways than the interaction of 2, so postestimation tools such as the estimate, lsmestimate and effectplot are even more crucial for full interpration of the interaction. In a 3-way interaction the interactions of each pair of variables is allowed to vary with levels of the third variable. We call these interactions across levels of the third variable conditional interactions here. In contrast, in a 2-way interaction model, these 2-way interactions are constrained to be constant across levels of all other predictors.
Not only can we estimate these conditional interactions, we can compare them, to see if the 2 variables interact in the same way across levels of the third variable. Moreover, these conditional interactions can be further decomposed into simple effects and slopes using the same methods described above, although the coding will be more complex because of the inclusion of the 3-way interaction coefficients.
Let us take an example where we are interacting a 2 level-categorical variable \(X\), which takes the values (0,1), a 3-level categorical \(M\) which takes the values (1,2,3) and a continuous variable \(Z\). The decomposition of this interaction could entail:
- Estimating and comparing the conditional interaction of \(X\) and \(Z\) at each of the 3 levels of \(M\). Each conditional interaction can further be decomposed into simple slopes of \(Z\) at the 2 levels of \(X\), or the simple effect of \(X\) at various levels of continuous \(Z\).
- Estimating and comparing the conditional interaction of \(M\) and \(Z\) at each of the 2 levels of \(M\). These interactions can further be decomposed into the simple slopes of \(Z\) at the 3 levels of \(M\), or the simple effects of \(M\) (3 different simple effects) at various levels of continuous \(Z\).
- Estimating and comparing the conditional interaction of \(X\) and \(M\) at various levels of continuous \(Z\). There are potentially and infininte number of these conditional interactions, but we can choose substantively important values of \(Z\) at which to evaluate the conditional interaction of \(X\) and \(M\). These conditional interactions can be further decomposed into the simple effects of \(X\) at \(M\) and the simple effects of \(M\) at \(X\).
To formulate the regression equation of the 3-way interaction model of regression \(Y\) on \(X\), \(M\), and \(Z\), we essentially take the regression equation for the 2-way interaction of categorical \(Y\) on \(X\) and categorical \(M\) (section 5.1 above) and multiply it by the equation for the regression of \(Y\) on \(Z\). The resulting regression equation is: \begin{align} Y’ &= \beta_0 \\ &+ \beta_{x0}(X=0) \\ &+ \beta_{m1}(M=1) + \beta_{m2}(M=2) \\ &+ \beta_{z}Z \\ &+ \beta_{x0m1}(X=0,M=1) + \beta_{x0m2}(X=0,M=2) \\ &+ \beta_{x0z}(X=0)*Z \\ &+ \beta_{m1z}(M=1)*Z + \beta_{m2z}(M=2)*Z \\ &+ \beta_{x0m1z}(X=0,M=1)*Z + \beta_{x0m2z}(X=0,M=2)*Z \end{align}
We must keep in mind 3 reference levels when interpreting the coefficients (using SAS default reference levels), \(X=1\), \(M=3\), and \(Z=0\). All of the coefficients except for the 3-way interaction coefficients are interpreted at some reference level of one or more of the 3 predictors. Here are the interpretations:
-
- \(\beta_0\): the expected value of \(Y\) when \(X=1\), \(M=3\), and \(Z=0\).
- \(\beta_{x0}\): the simple effect of \(X=0\) vs \(X=1\) when \(M=3\) and \(Z=0\).
- \(\beta_{m1}\): the simple effect of \(M=1\) vs \(M=3\) when \(X=1\) and \(Z=0\).
- \(\beta_{m2}\): the simple effect of \(M=2\) vs \(M=3\) when \(X=1\) and \(Z=0\).
- \(\beta_z\): the simple slope of \(Z\) when \(X=1\) and \(M=3\).
- \(\beta_{x0m1}\): the additional effect of \(X=0\) vs \(X=1\) when \(M=1\), compared to\(M=3\), while \(Z=0\); or the additional effect of \(M=1\) vs \(M=3\) when \(X=1\), compared to \(X=0\), while \(Z=0\)
- \(\beta_{x0m2}\): the additional effect of \(X=0\) vs \(X=1\) when \(M=2\), compared to\(M=3\), while \(Z=0\); or the additional effect of \(M=2\) vs \(M=3\) when \(X=1\), compared to \(X=0\), while \(Z=0\)
- \(\beta_{x0z}\): the change in the effect of \(X=0\) vs \(X=1\) per unit-increase in \(Z\), while \(M=3\); or the change in the simple slope of \(Z\) for \(X=0\) compared to \(X=1\) while \(M=3\)
- \(\beta_{m1z}\): the change in the effect of \(M=1\) vs \(M=3\) per unit-increase in \(Z\), while \(X=1\); or the change in the simple slope of \(Z\) for \(M=1\) compared to \(M=3\) while \(X=1\)
- \(\beta_{m2z}\): the change in the effect of \(M=2\) vs \(M=3\) per unit-increase in \(Z\), while \(X=1\); or the change in the simple slope of \(Z\) for \(M=2\) compared to \(M=3\) while \(X=1\)
- \(\beta_{x0m1z}\): the change per unit-increase in \(Z\) in the additional effect of \(X=0\) vs \(X=1\) when \(M=1\), compared to \(M=3\); or the change per unit-increase in \(Z\) in the additional effect of \(M=1\) vs \(M=3\) when \(X=1\), compared to \(X=0\); or the additional change in the simple slope of \(Z\) for \(X=0\) compared to \(X=1\) when comparing \(M=1\) to \(M=3\); or the additional change in the simple slope of \(Z\) for \(M=1\) compared to \(M=3\) when comparing \(X=0\) to \(X=1\)
- \(\beta_{x0m2z}\): the change per unit-increase in \(Z\) in the additional effect of \(X=0\) vs \(X=1\) when \(M=2\), compared to \(M=3\); or the change per unit-increase in \(Z\) in the additional effect of \(M=2\) vs \(M=3\) when \(X=1\), compared to \(X=0\); or the additional change in the simple slope of \(Z\) for \(X=0\) compared to \(X=1\) when comparing \(M=2\) to \(M=3\); or the additional change in the simple slope of \(Z\) for \(M=2\) compared to \(M=3\) when comparing \(X=0\) to \(X=1\)
The three way interaction are not easy to interpret without additional analyses.
6.2 Linear regression, 3-way categorical-categorical-continuous interaction: example model
We will estimate the regression of loss on the 3-way interaction of female (2-category), prog (3-category), and hours (continuous). Below, we use proc glm to estimate our model, which we then store for later use in proc plm.
proc glm data = exercise order=internal; class female prog; model loss = female|prog|hours / solution; store catcatcon; run;
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| female | 1 | 35.689362 | 35.689362 | 1.06 | 0.3045 |
| prog | 2 | 2770.894770 | 1385.447385 | 40.98 | <.0001 |
| female*prog | 2 | 2303.402968 | 1151.701484 | 34.07 | <.0001 |
| hours | 1 | 2792.113816 | 2792.113816 | 82.59 | <.0001 |
| hours*female | 1 | 31.478835 | 31.478835 | 0.93 | 0.3348 |
| hours*prog | 2 | 5065.441698 | 2532.720849 | 74.91 | <.0001 |
| hours*female*prog | 2 | 889.207127 | 444.603563 | 13.15 | <.0001 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| | |
|---|---|---|---|---|---|
| Intercept | 0.88416698 | B | 1.79656989 | 0.49 | 0.6227 |
| female male | 2.91521844 | B | 2.67025153 | 1.09 | 0.2752 |
| female female | 0.00000000 | B | . | . | . |
| prog jogging | -15.81177139 | B | 2.76073786 | -5.73 | <.0001 |
| prog swimming | 19.51420901 | B | 2.71002110 | 7.20 | <.0001 |
| prog reading | 0.00000000 | B | . | . | . |
| female*prog male jogging | 14.98213316 | B | 3.97655737 | 3.77 | 0.0002 |
| female*prog male swimming | -18.70330012 | B | 3.90284003 | -4.79 | <.0001 |
| female*prog male reading | 0.00000000 | B | . | . | . |
| female*prog female jogging | 0.00000000 | B | . | . | . |
| female*prog female swimming | 0.00000000 | B | . | . | . |
| female*prog female reading | 0.00000000 | B | . | . | . |
| hours | -2.24126294 | B | 0.86216244 | -2.60 | 0.0095 |
| hours*female male | -1.53710579 | B | 1.27130616 | -1.21 | 0.2270 |
| hours*female female | 0.00000000 | B | . | . | . |
| hours*prog jogging | 12.05590113 | B | 1.35305435 | 8.91 | <.0001 |
| hours*prog swimming | 6.60149491 | B | 1.31010340 | 5.04 | <.0001 |
| hours*prog reading | 0.00000000 | B | . | . | . |
| hours*female*prog male jogging | -3.91288821 | B | 1.92424405 | -2.03 | 0.0423 |
| hours*female*prog male swimming | 6.23323931 | B | 1.88426035 | 3.31 | 0.0010 |
| hours*female*prog male reading | 0.00000000 | B | . | . | . |
| hours*female*prog female jogging | 0.00000000 | B | . | . | . |
| hours*female*prog female swimming | 0.00000000 | B | . | . | . |
| hours*female*prog female reading | 0.00000000 | B | . | . | . |
We see in the Type III table above that overall our 3-way interaction is significant. The direct interpretation of the 3-way interaction coefficients is quite complex and difficult to convey to an audience clearly; typically not all of of the many interpretations are of interest, so a focused analysis of conditional interactions, simple slopes and simple effects is ususally undertaken.
6.3 Linear regression, 3-way categorical-categorical-continuous interaction: simple slopes-focused analysis
Imagine our focus when embarking on this research project is to estimate which groups benefit most from increasing the weekly number of hours of exercise in each program. We might first address this question by estimating the slope of hours in each pairing of gender and program. We approach this section of the seminar by showing how we might use the tools in proc plm to answer research questions posed in a simple-slope-focused analysis. We will take a bottom-up approach, where we first analyze simple effects, then conditional interactions, as the coding will be easier.
6.3.1 3-way simple slopes: what are the simple slopes in each pairing of levels of the 2 factors?
We again turn to the estimate statement to calculate our simple slopes. Generally when estimating the simple slope of a continuous variable interacted with 2 categorical variables, on the estimate statement, place a value of 1 after the coefficient for the slope variable alone, after the 2 2-way interaction coefficient involving the slope variable with each of the two groups making up the interaction, and the 3-way interaction coefficient of the slope and the 2 groups. For example, if we would like to estimate the simple slope of hours for females in the jogging program, we would apply a value of 1 to the following coefficients: hours, hours by female, hours by jogging, and hours by female by jogin (even if the coefficient has been constrained to 0 by SAS — see the table of regression coefficients above):
proc plm restore=catcatcon; estimate 'hours slope, male prog=jogging' hours 1 hours*female 1 0 hours*prog 1 0 0 hours*female*prog 1 0 0 0 0 0, 'hours slope, male prog=swimming' hours 1 hours*female 1 0 hours*prog 0 1 0 hours*female*prog 0 1 0 0 0 0, 'hours slope, male prog=reading' hours 1 hours*female 1 0 hours*prog 0 0 1 hours*female*prog 0 0 1 0 0 0, 'hours slope, female prog=jogging' hours 1 hours*female 0 1 hours*prog 1 0 0 hours*female*prog 0 0 0 1 0 0, 'hours slope, female prog=swimming' hours 1 hours*female 0 1 hours*prog 0 1 0 hours*female*prog 0 0 0 0 1 0, 'hours slope, female prog=reading' hours 1 hours*female 0 1 hours*prog 0 0 1 hours*female*prog 0 0 0 0 0 1 / e adj=bon; run;
| Estimates Adjustment for Multiplicity: Bonferroni | ||||||
|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| hours slope, male prog=jogging | 4.3646 | 0.9995 | 888 | 4.37 | <.0001 | <.0001 |
| hours slope, male prog=swimming | 9.0564 | 0.9804 | 888 | 9.24 | <.0001 | <.0001 |
| hours slope, male prog=reading | -3.7784 | 0.9343 | 888 | -4.04 | <.0001 | 0.0003 |
| hours slope, female prog=jogging | 9.8146 | 1.0428 | 888 | 9.41 | <.0001 | <.0001 |
| hours slope, female prog=swimming | 4.3602 | 0.9864 | 888 | 4.42 | <.0001 | <.0001 |
| hours slope, female prog=reading | -2.2413 | 0.8622 | 888 | -2.60 | 0.0095 | 0.0569 |
Increasing the number of weekly hours significantly increases the expected weight loss for both genders in both the jogging and swimming programs. In contrast, in the reading program, increasing the number of weekly hours decreases expected weight loss (not significantly so for females after Bonferroni adjustment). We next investigate whether these simple slopes differ.
6.3.2 3-way simple slopes: are the conditional interactions of one factor and the continuous variable signficant within each level of the other factor?
We might wonder whether the hours slope for each gender differs within each program, that is, do hours and female significantly interact within each level of prog? These are tests of the significance of three 2-way conditional interactions. We use estimate statements to test the difference between hours slopes for each gender within each program by subtracting the values across coefficients for the estimates of the simple slopes. Notice that the hours coefficients cancel to 0, an indication that we are now estimating and testing interactions rather than simple slopes:
proc plm restore=catcatcon; estimate 'diff hours slope, male-female prog=1' hours*female 1 -1 hours*female*prog 1 0 0 -1 0 0, 'diff hours slope, male-female prog=2' hours*female 1 -1 hours*female*prog 0 1 0 0 -1 0, 'diff hours slope, male-female prog=3' hours*female 1 -1 hours*female*prog 0 0 1 0 0 -1 / e adj=bon; run;
| Estimates Adjustment for Multiplicity: Bonferroni | ||||||
|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| diff hours slope, male-female prog=1 | -5.4500 | 1.4445 | 888 | -3.77 | 0.0002 | 0.0005 |
| diff hours slope, male-female prog=2 | 4.6961 | 1.3908 | 888 | 3.38 | 0.0008 | 0.0023 |
| diff hours slope, male-female prog=3 | -1.5371 | 1.2713 | 888 | -1.21 | 0.2270 | 0.6809 |
It appears that males and females benefit differently in increasing the number of hours of exercise in the jogging and swimming programs, but not in the reading program. In other words, gender and hours interact significantly in 2 of the three programs.
6.3.3 3-way simple slopes: are the conditional interactions different from each other?
Finally, we might be interested in whether the difference between hours slopes for each gender varies between programs — in other words, does the interaction of hours and gender differ between programs? A test of the difference of 2-way interactions is a test of the 3-way interaction. We know from the Type III test of our 3-way interaction that at least 1 of the conditional interactions of gender and hours should differ between programs. We in fact get two of these tests of differences between conditional interactions for “free” in the regression table – jogging vs reading and swimming vs reading (and both are in fact significant).
We can use the estimate statement to test the third comparison – whether the interaction of hours and gender differs between the jogging and swimming programs. We again will subtract values across coefficients, this time between the conditional interaction estimates in the previous section. Notice that the 2-way interaction coefficients cancel to 0. We demonstrate all 3-way comparisons with the estimate statement, though notice that the two 3-way interaction coefficients are reproduced:
proc plm restore=catcatcon;
estimate 'diff diff hours slope, male-female prog=1-prog=2' hours*female*prog 1 -1 0 -1 1 0,
'diff diff hours slope, male-female prog=1-prog=3' hours*female*prog 1 0 -1 -1 0 1,
'diff diff hours slope, male-female prog=2-prog=3' hours*female*prog 0 1 -1 0 -1 1 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| diff diff hours slope, male-female prog=1-prog=2 | -10.1461 | 2.0052 | 888 | -5.06 | <.0001 |
| diff diff hours slope, male-female prog=1-prog=3 | -3.9129 | 1.9242 | 888 | -2.03 | 0.0423 |
| diff diff hours slope, male-female prog=2-prog=3 | 6.2332 | 1.8843 | 888 | 3.31 | 0.0010 |
It appears the manner in which the slopes of hours differ for each gender is different bewteen the jogging and reading programs.
6.3.4 3-way simple slopes: graphing the simple slope analysis of the 3-way interaction
The slicefit graph in the effectplot statement in proc plm provides an easy way to visualize all of the analyses we performed above. We have analyzed the conditional interactions of hours and gender across programs, so we specify that hours appear on the x-axis, that we plot separate lines (sliceby=) by gender, and generate separate plots by program (plotby=).
proc plm restore=catcatcon; effectplot slicefit (x=hours sliceby=female plotby=prog) / clm; run;
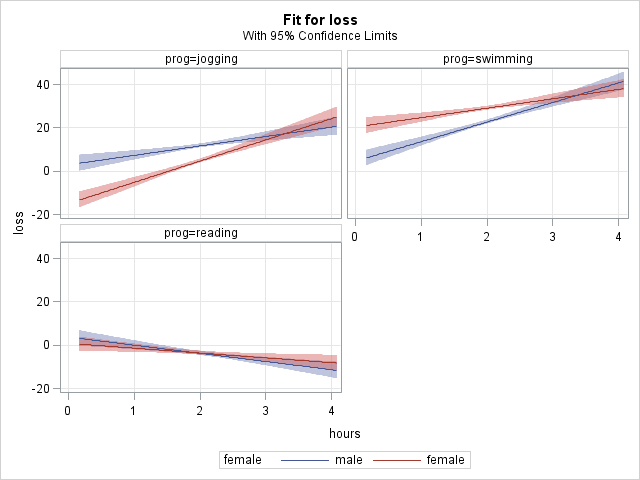
In the graph each line is a simple slope of hours. We see that between genders, the slopes appear different in the jogging and swimming programs but not in the reading program. Moreover, the manner in which the slopes differ appears to vary between the jogging and swimming programs – namely that females benefit more strongly from increasing the number hours in the jogging program, while males benefit more strongly in the swimming program.
We can of course approach the simple slope analysis from another perspective by switching the roles of the factors female and prog. Namely, we can examine the interaction of hours and program within each gender — do the slopes of hours significantly differ among programs within each gender? Are the conditional interactions different between genders. Below are code and results to answer those questions. NOTE: the joint option is used to specify a joint test of several coefficients – whether any of them are signficantly different from 0 — as an overall test of the conditional interaction within each gender.
proc plm restore=catcatcon; estimate 'diff hours slope, male prog=1 - prog=2' hours*prog 1 -1 0 hours*female*prog 1 -1 0 0 0 0, 'diff hours slope, male prog=1 - prog=3' hours*prog 1 0 -1 hours*female*prog 1 0 -1 0 0 0, 'diff hours slope, male prog=2 - prog=3' hours*prog 0 1 -1 hours*female*prog 0 1 -1 0 0 0 / e joint; estimate 'diff hours slope, female prog=1 - prog=2' hours*prog 1 -1 0 hours*female*prog 0 0 0 1 -1 0, 'diff hours slope, female prog=1 - prog=3' hours*prog 1 0 -1 hours*female*prog 0 0 0 1 0 -1, 'diff hours slope, female prog=2 - prog=3' hours*prog 0 1 -1 hours*female*prog 0 0 0 0 1 -1 / e joint; run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| diff hours slope, male prog=1 – prog=2 | -4.6917 | 1.4001 | 888 | -3.35 | 0.0008 |
| diff hours slope, male prog=1 – prog=3 | 8.1430 | 1.3682 | 888 | 5.95 | <.0001 |
| diff hours slope, male prog=2 – prog=3 | 12.8347 | 1.3543 | 888 | 9.48 | <.0001 |
| F Test for Estimates | ||||
|---|---|---|---|---|
| Label | Num DF | Den DF | F Value | Pr > F |
| diff hours slope, male prog=1 – prog=2 | 2 | 888 | 46.33 | <.0001 |
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| diff hours slope, female prog=1 – prog=2 | 5.4544 | 1.4354 | 888 | 3.80 | 0.0002 |
| diff hours slope, female prog=1 – prog=3 | 12.0559 | 1.3531 | 888 | 8.91 | <.0001 |
| diff hours slope, female prog=2 – prog=3 | 6.6015 | 1.3101 | 888 | 5.04 | <.0001 |
| F Test for Estimates | ||||
|---|---|---|---|---|
| Label | Num DF | Den DF | F Value | Pr > F |
| diff hours slope, female prog=1 – prog=2 | 2 | 888 | 40.72 | <.0001 |
proc plm restore=catcatcon;
estimate 'diff diff hours slope, prog=1-prog=2, male-female' hours*female*prog 1 -1 0 -1 1 0,
'diff diff hours slope, prog=1-prog=3, male-female' hours*female*prog 1 0 -1 -1 0 1,
'diff diff hours slope, prog=2-prog=3, male-female' hours*female*prog 0 1 -1 0 -1 1 / e;
run;
| Estimates | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| diff diff hours slope, prog=1-prog=2, male-female | -10.1461 | 2.0052 | 888 | -5.06 | <.0001 |
| diff diff hours slope, prog=1-prog=3, male-female | -3.9129 | 1.9242 | 888 | -2.03 | 0.0423 |
| diff diff hours slope, prog=2-prog=3, male-female | 6.2332 | 1.8843 | 888 | 3.31 | 0.0010 |
proc plm restore=catcatcon; effectplot slicefit (x=hours sliceby=prog plotby=female) / clm; run;
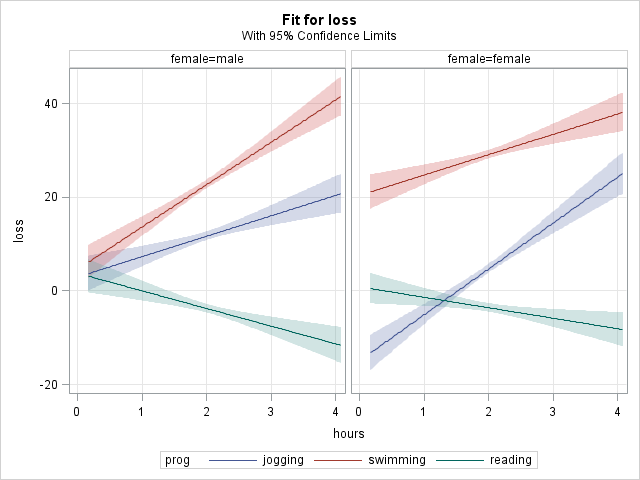
6.4 Linear regression, 3-way categorical-categorical-continuous interaction: simple effects-focused analysis
Imagine now instead that we are more focused on gender effects in each program and how these effects may be moderated by the hours of exercise. We organized this simple effects analysis as a series of research questions proceeding again from the bottom-up in terms of effect complexity.
6.4.1 3-way simple effects: what are the simple effects of one factor across levels of the other factor at selected values of the covariate?
We first might be interested in estimating the difference in expected loss between genders in each program at 1.51, 2, and 2.5 weekly hours of exercise (mean-sd, mean, mean+sd of hours). We will demonstrate the use of both the slice and the lsmestimate statement to estimate our simple effects and test them for signficance. NOTE: In both statements, we use the at option to specify at which number of hours we would like these simple effects evaluated. We can only specify one value of hours per slice or lsmestimate statement.
proc plm restore=catcatcon; slice female*prog / sliceby=prog diff plots=none nof e means at hours=1.51; slice female*prog / sliceby=prog diff plots=none nof e means at hours=2; slice female*prog / sliceby=prog diff plots=none nof e means at hours=2.5; run;
The output of these slice statements is quite voluminous so we will omit it (instead we will use the lsmestimate output which is more compact), but one nice feature is that we get estimates of the expected means involved in the simple effect analysis with the means option.
proc plm restore=catcatcon; lsmestimate female*prog 'male-female, prog=jogging(1) hours=1.51' [1, 1 1] [-1, 2 1], 'male-female, prog=swimming(2) hours=1.51' [1, 1 2] [-1, 2 2], 'male-female, prog=reading(3) hours=1.51' [1, 1 3] [-1, 2 3] / e adj=bon at hours=1.51; lsmestimate female*prog 'male-female, prog=jogging(1) hours=2' [1, 1 1] [-1, 2 1], 'male-female, prog=swimming(2) hours=2' [1, 1 2] [-1, 2 2], 'male-female, prog=reading(3) hours=2' [1, 1 3] [-1, 2 3] / e adj=bon at hours=2; lsmestimate female*prog 'male-female, prog=jogging(1) hours=2.5' [1, 1 1] [-1, 2 1], 'male-female, prog=swimming(2) hours=2.5' [1, 1 2] [-1, 2 2], 'male-female, prog=reading(3) hours=2.5' [1, 1 3] [-1 ,2 3] / e adj=bon at hours=2.5; run;
| Least Squares Means Estimates Adjustment for Multiplicity: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Effect | Label | hours | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female*prog | male-female, prog=jogging(1) hours=1.51 | 1.51 | 9.6679 | 0.9620 | 888 | 10.05 | <.0001 | <.0001 |
| female*prog | male-female, prog=swimming(2) hours=1.51 | 1.51 | -8.6969 | 0.9458 | 888 | -9.20 | <.0001 | <.0001 |
| female*prog | male-female, prog=reading(3) hours=1.51 | 1.51 | 0.5942 | 0.9451 | 888 | 0.63 | 0.5297 | 1.0000 |
| Least Squares Means Estimates Adjustment for Multiplicity: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Effect | Label | hours | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female*prog | male-female, prog=jogging(1) hours=2 | 2.00 | 6.9974 | 0.6730 | 888 | 10.40 | <.0001 | <.0001 |
| female*prog | male-female, prog=swimming(2) hours=2 | 2.00 | -6.3958 | 0.6718 | 888 | -9.52 | <.0001 | <.0001 |
| female*prog | male-female, prog=reading(3) hours=2 | 2.00 | -0.1590 | 0.6732 | 888 | -0.24 | 0.8134 | 1.0000 |
| Least Squares Means Estimates Adjustment for Multiplicity: Bonferroni | ||||||||
|---|---|---|---|---|---|---|---|---|
| Effect | Label | hours | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| female*prog | male-female, prog=jogging(1) hours=2.5 | 2.50 | 4.2724 | 1.0018 | 888 | 4.26 | <.0001 | <.0001 |
| female*prog | male-female, prog=swimming(2) hours=2.5 | 2.50 | -4.0477 | 0.9779 | 888 | -4.14 | <.0001 | 0.0001 |
| female*prog | male-female, prog=reading(3) hours=2.5 | 2.50 | -0.9275 | 0.8968 | 888 | -1.03 | 0.3013 | 0.9039 |
Gender is a signficant effect in both the jogging and swimming programs, but not reading, no matter the number of hours exercised. However, the gender differences appear to decrease as the number of hours increases.
6.4.2 3-way simple effects: are the conditional interactions of the 2 factors significant at selected values of the covariate?
We might next be interested in whether the gender differences are significantly different among programs at the selected number of hours (1.51, 2, 2.5). That is, do gender and program signficantly interact at each of those hours? These questions can both be answered by simply adding the joint option to each lsmestimate statement that codes for the set of gender comparisons across programs within a set number of hours:
proc plm restore=catcatcon; lsmestimate female*prog 'diff male-female, prog=1 - prog=2, hours=1.51' [1, 1 1] [-1, 2 1] [-1, 1 2] [1, 2 2], 'diff male-female, prog=1 - prog=3, hours=1.51' [1, 1 1] [-1, 2 1] [-1, 1 3] [1, 2 3], 'diff male-female, prog=2 - prog=3, hours=1.51' [1, 1 2] [-1, 2 2] [-1, 1 3] [1, 2 3] / e at hours=1.51 joint; lsmestimate female*prog 'diff male-female, prog=1 - prog=2, hours=2' [1, 1 1] [-1, 2 1] [-1, 1 2] [1, 2 2], 'diff male-female, prog=1 - prog=3, hours=2' [1, 1 1] [-1, 2 1] [-1, 1 3] [1, 2 3], 'diff male-female, prog=2 - prog=3, hours=2' [1, 1 2] [-1, 2 2] [-1, 1 3] [1, 2 3] / e at hours=2 joint; lsmestimate female*prog 'diff male-female, prog=1 - prog=2, hours=2.5' [1, 1 1] [-1, 2 1] [-1, 1 2] [1, 2 2], 'diff male-female, prog=1 - prog=3, hours=2.5' [1, 1 1] [-1, 2 1] [-1, 1 3] [1, 2 3], 'diff male-female, prog=2 - prog=3, hours=2.5' [1, 1 2] [-1, 2 2] [-1, 1 3] [1, 2 3] / e at hours=2.5 joint; run;
| F Test for Least Squares Means Estimates | |||||
|---|---|---|---|---|---|
| Effect | Label | Num DF | Den DF | F Value | Pr > F |
| female*prog | diff male-female, prog=1 – prog=2, hours=1.51 | 2 | 888 | 92.68 | <.0001 |
| F Test for Least Squares Means Estimates | |||||
|---|---|---|---|---|---|
| Effect | Label | Num DF | Den DF | F Value | Pr > F |
| female*prog | diff male-female, prog=1 – prog=2, hours=2 | 2 | 888 | 99.33 | <.0001 |
| F Test for Least Squares Means Estimates | |||||
|---|---|---|---|---|---|
| Effect | Label | Num DF | Den DF | F Value | Pr > F |
| female*prog | diff male-female, prog=1 – prog=2, hours=2.5 | 2 | 888 | 18.00 | <.0001 |
Gender and program significantly interact at 1.51, 2, and 2.5 hours of exercise.
6.4.3 3-way simple effects: are the conditional interactions different?
The significance of the Type III test of the 3-way interaction indicates that the conditional interactions of gender and program vary significantly as the number of hours exercised changes. The 3-way interaction coefficients tell us that the difference in gender effects between jogging vs reading and swimming vs reading vary with hours. The final comparison, whether the difference in gender effects between jogging vs reading varies signifcantly with hours. We can address this comparison (which we actually addressed before in the simple slopes analysis) with an estimate statement (not an lsmestimate statement because we are varying the number of hours across means being compared):
proc plm restore=catcatcon; estimate 'change in diff male-female, prog=1-prog=2, per unit increase hours' hours*female*prog 1 -1 0 -1 1 0 / e; run;
| Estimate | |||||
|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| |
| change in diff male-female, prog=1-prog=2, per unit increase hours | -10.1461 | 2.0052 | 888 | -5.06 | <.0001 |
It appears that the difference in gender effects between the jogging and swimming program also varies with hours.
6.4.4 3-way simple effects: graphing the simple-effects analysis of the 3-way interaction
We will use the interaction type of graph in the effectplot statement in proc plm to plot our simple effects. We request that female appear on the x-axis, we plot separate lines(sliceby=) by prog, and use the at option to specify levels of hours at which to generate separate plots.
proc plm restore=catcatcon; effectplot interaction (x=female sliceby=prog) / at(hours = 1.51 2 2.5) clm connect; run;
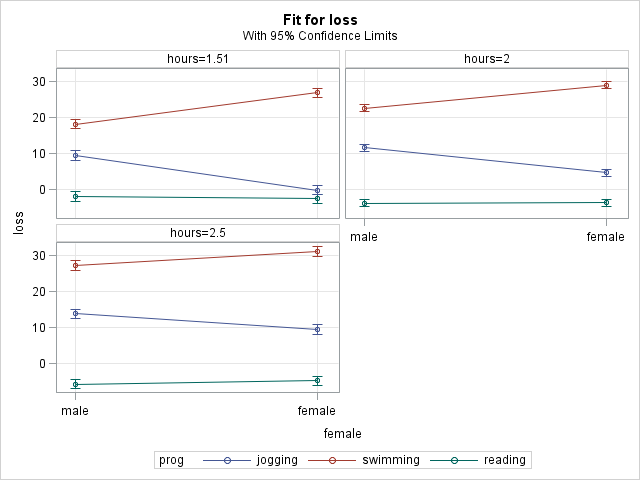
In the plot we see that generally there appear to be gender effects in the jogging and swimming programs, while not so in the reading program (flat lines). The gender effects do appear to differ across programs at each level of hours. However, the differences between gender effects are larger at hours=1.51 than hours=2.5 (the lines are less parallel at hours=1.51).
7. Logistic regression
7.1 Background
In logistic regression, the outcome is binary (0/1, often defined as “success” and “failure” for convenience) and we are interested in modeling factors that affect the probability of the outcome. It is generally inappropriate to model a binary outcome in linear regression because several of the underlying assumptions will be violated (homoskedasticity of errors, normality of residuals, linearity of outcome with predictors). Modeling probabilities directly is difficult because of their very restricted range, 0 to 1 — it can be difficult to restrict the effect of a continuous predictor to lie within this range. In logistic regression, this problem is solved by transforming probabilities so that the transformed quantity can take on an infinite range of values. This transformation of the probability of the outcome \(p\) is the logit transformation:
$$logit(p) = log(\frac{p}{1-p})$$
In logisitic regression, the logit of p is modeled as having a linear relationship with the predictors:
$$logit(p) = \beta_0 + \beta_1X_1 +\beta_2X_2$$ $$log(\frac{p}{1-p}) = \beta_0 + \beta_1X_1 +\beta_2X_2$$
The logit of \(p\) is also the log-odds of the event with probability \(p\), as we are taking the natural logarithm of the odds given \(p\), where odds given \(p\) is defined as:
$$odds(p) = \frac{p}{1-p}$$
The odds can be interpreted as how many positive outcomes (successes) we expect per negative outcome (failures). The odds has a monotonic relationship with the probability \(p\), so interpreting the direction of the relationship is easy.
It is important to understand odds conceptually, because the exponentiated coefficients in logistic regression are often reported and are thus interpreted as odds ratios. As the name implies, odds ratios express the ratio of two odds, for instance the two expected odds of the outcome in females vs males, or when hours = 1 vs hours = 2. Odds ratios describe multiplicative changes in the odds of the outcome per additive change in the predictors.
Odds ratios are the exponentiated coefficients in logistic regression. Remember that the logit or log-odds of \(p\), not \(p\) itself, is modeled as having a linear relationship with the predictors. Let’s say we are modeling the relationship between the log-odds of an outcome with probability \(p\) and a single binary predictor \(X\): $$log(\frac{p}{1-p}) = \beta_0 + \beta_1X$$
The log-odds estimates for \(X=0\) and \(X=1\) are, respectively: $$log(\frac{p_1}{1-p_1}) = \beta_0$$ $$log(\frac{p_2}{1-p_2}) = \beta_0 + \beta_1$$
The difference between the two log-odds estimate is then: $$log(\frac{p_2}{1-p_2}) – log(\frac{p_1}{1-p_1}) = \beta_1$$
Rembering the two equalities: $$\frac{p}{1-p} = odds(p)$$ $$logA-logB = log\frac{A}{B}$$
We get: $$log\frac{odds_2}{odds_1} = \beta_1$$ $$logOR = \beta_1$$
Exponentiating: $$exp(logOR) = exp(\beta_1)$$ $$OR = exp(\beta_1)$$
It will help us to think of odds ratios as exponentiated differences to facilitate our estimate statement coding.
One reason that odds ratios may be reported is that they express an effect of a predictor that is constant across the range of that predictor — the odds ratios of outcomes with \(X=1\) vs \(X=0\) is the same as the odds ratio of outcomes with \(X=11\) and \(X=12\), given all other predictors are held constant. This allows the effect of a predictor to be summarized by one value. In contrast, the effect on the probability of the outcome is not constant across the range of the predictor in logistic regression. The difference between the expected probabilities of outcome with \(X=1\) vs \(X=0\) will not be the same as the difference between expected probabilities of outcomes with \(X=11\) and \(X=12\), if modeled in logistic regression. This is true because a non-linear transformation (the logit) is applied to the probability of the outcome before it is modeled as having a linear relationship with the predictors.
However odds ratios can be misleading. Two outcomes with probabilities \(p_1=.001\) and \(p_2=.003\) have the same odds ratio as the outcomes with probabilities \(p_3=.25\) and \(p_4=.5\), both with odds ratios equal to 3. However, the absolute difference of each pair of probabilities is quite different, .002 vs .25. It might be misleading to claim that two such effects are the same, even though they have the same odds ratio. We thus recommend that researchers get an idea of the probabilities underlying these odds ratios.
One final note: the exponentiated coefficients for the intercept and for any interaction coefficient are not interepreted as odds ratios. The exponentiated intercept is interpreted as the odds of the outcome when all predictors are equal to 0. We explain how to interpret exponentiated 2-way interaction coefficients below.
7.2 Logistic regression, categorical-by-continuous interaction: example model
Included with the dataset accompanying this seminar is the binary variable satisfied, which is equal to 0 if the subject was not satisfied with the weight loss achieved by their program and a 1 if the subject was satisfied. We will model whether the average number of weekly hours of exercise interacts with the program type in predicting the probability that the subject was satisified. We first run the model in proc logistic so that we may get a regression equation:
proc logistic data = exercise descending; class prog / param=glm order=internal; model satisfied = prog|hours / expb; store logit; run;
Notice in the code above:
descendingon theproc logisticstatement will specify that SAS models that probability that the outcome=1, rather than outcome=0, which is the default- we again specify
param=glmon theclassstatement to request “glm” rather than the default “effect” coding, which expresses class effects as differences from a reference group and the grand mean, respectively - we also specify
order=internalon theclassstatement so that the categories of prog are ordered by their internal numbering rather than their formats - we request that the exponentiated coefficients be displayed with
expb, although we should be careful in their interpreation - we create an item
storefor later use inproc plm
| Type 3 Analysis of Effects | |||
|---|---|---|---|
| Effect | DF | Wald Chi-Square | Pr > ChiSq |
| prog | 2 | 40.2984 | <.0001 |
| hours | 1 | 33.0890 | <.0001 |
| hours*prog | 2 | 36.6499 | <.0001 |
| Analysis of Maximum Likelihood Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald Chi-Square | Pr > ChiSq | Exp(Est) | |
| Intercept | 1 | 0.5739 | 0.4619 | 1.5437 | 0.2141 | 1.775 | |
| prog | jogging | 1 | -4.1262 | 0.7782 | 28.1150 | <.0001 | 0.016 |
| prog | swimming | 1 | -3.9372 | 0.7624 | 26.6670 | <.0001 | 0.020 |
| prog | reading | 0 | 0 | . | . | . | . |
| hours | 1 | -0.3156 | 0.2204 | 2.0499 | 0.1522 | 0.729 | |
| hours*prog | jogging | 1 | 1.7287 | 0.3687 | 21.9835 | <.0001 | 5.634 |
| hours*prog | swimming | 1 | 1.9407 | 0.3697 | 27.5591 | <.0001 | 6.964 |
| hours*prog | reading | 0 | 0 | . | . | . | . |
The resulting regression equation is \begin{align} log(\frac{p}{1-p}) &= .57 \\ &- 4.13*(prog=1) -3.94*(prog=2) \\ &- .32*hours \\ &+ 1.73*hours*(prog=1) + 1.94*(prog=2) \end{align}
Normally, the simple slope of hours would be expressed as some linear combination of coefficients.
$$slope_{hours|prog=1} = -.32 + 1.73 = 1.41$$ $$slope_{hours|prog=2} = -.32 + 1.94 = 1.62$$ $$slope_{hours|prog=3} = -.32$$
However, in a logistic regression model, linear combinations of the coefficients have units log-odds, which are hard to interpret. Thus, the linear combinations are often exponentiated so that the simple slopes are expressed as simple odds ratios.
$$OR_{hours|prog=1} = exp(1.41)$$ $$OR_{hours|prog=2} = exp(1.62)$$ $$OR_{hours|prog=3} = exp(-.32)$$
The oddsratio statement in proc logistic provides an easy way to estimate these simple odds ratios.
7.3 Logistic regression, categorical-by-continuous interaction: calculating and graphing simple odds ratios
The oddsratio statement in proc logistic allows easy decomposition of an interaction into simple odds ratio. Not only are the odds ratios and confidence interals calculated, but an odds ratio plot is produced as well.
We specify that we would like odds ratios for hours, across all levels of prog.
proc logistic data = exercise descending; class prog / param=glm order=internal; model satisfied = prog|hours / expb; oddsratio hours / at(prog=all); store logit; run;
| Odds Ratio Estimates and Wald Confidence Intervals | |||
|---|---|---|---|
| Odds Ratio | Estimate | 95% Confidence Limits | |
| hours at prog=jogging | 4.109 | 2.302 | 7.333 |
| hours at prog=swimming | 5.079 | 2.839 | 9.086 |
| hours at prog=reading | 0.729 | 0.473 | 1.123 |
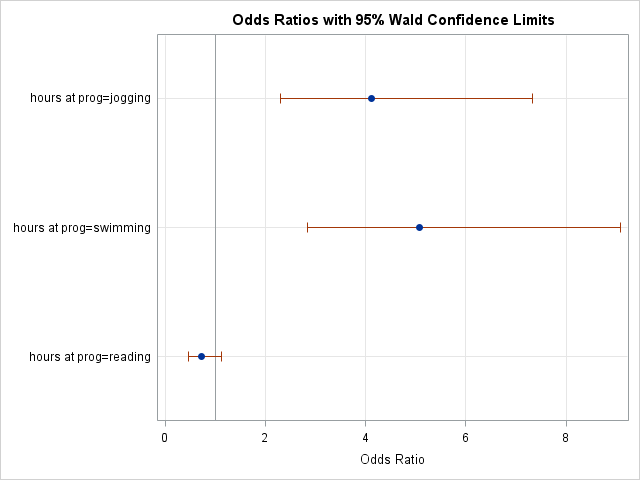
Because a difference of 0 in the log-odds of the outcome when exponentiated translates to an odds ratio of 1, we test odds ratios for significance against 1 rather than 0. Thus, confidence intervals that contain 1 denote non-significant effects. In the table above we see that the effect of number of weekly hours of exercise is significant in both the jogging and swimming programs, such that in both programs, increasing the number of hours increases the odds of satisfaction. Each additional hour increases the odds of satisfaction by a factor of 4.1 (310%) and 5.1 (410%) in the jogging and swimming programs, respectively. On the other hand, the effect of number of hours is not significant in the reading program as the confidence interval for the reading OR contains 1. The odds ratio plot graphs the point estimate of the odds ratio, with surrounding confidence intervals and a reference line at 1 for visual tests of significance.
7.4 Logistic regression, categorical-by-continuous interaction: comparing simple odds ratios and interpreting exponentiated interaction coefficients
We can also compare whether the simple odds ratios of hours are the same between programs. Two of the 2-way interactions coefficients explicitly test this — we already know that the effect of hours is different between jogging and rewading and between swimming and reading by the significant 2-way interaction coefficients (1.7287 and 1.9407). We will first use estimate statements to estimate the simple slopes of hours, which are then exponentiated with the exp option to yield simple odds ratios.
proc plm restore=logit; estimate 'hours OR, prog=1' hours 1 hours*prog 1 0 0, 'hours OR, prog=2' hours 1 hours*prog 0 1 0, 'hours OR, prog=3' hours 1 hours*prog 0 0 1 / e exp cl; run;
We omit the output but assure the reader that the odds ratios are the same as those estimated by the oddsratio statement. We next take the difference between these simple slopes and exponentiate the results, which are not to be interpreted as odds ratios.
proc plm restore=logit;
estimate 'ratio hours OR, prog=1/prog=2' hours*prog 1 -1 0,
'ratio hours OR, prog=1/prog=3' hours*prog 1 0 -1,
'ratio hours OR, prog=2 /prog=3' hours*prog 0 1 -1 / e exp cl;
run;
| Estimates | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | z Value | Pr > |z| | Alpha | Lower | Upper | Exponentiated | Exponentiated Lower | Exponentiated Upper |
| ratio hours OR, prog=1/prog=2 | -0.2119 | 0.4188 | -0.51 | 0.6128 | 0.05 | -1.0328 | 0.6089 | 0.8090 | 0.3560 | 1.8385 |
| ratio hours OR, prog=1/prog=3 | 1.7287 | 0.3687 | 4.69 | <.0001 | 0.05 | 1.0061 | 2.4514 | 5.6336 | 2.7349 | 11.6046 |
| ratio hours OR, prog=2 /prog=3 | 1.9407 | 0.3697 | 5.25 | <.0001 | 0.05 | 1.2161 | 2.6652 | 6.9635 | 3.3741 | 14.3715 |
In the “Estimate” column are the estimates of the differences in the simple slopes (expressed in log-odds units). Two of these estimates are the 2-way interaction coefficients in the regression table. In the “Exponentiated” column we see these quantities exponentiated. So how do we interpret these exponentiated differences in simple slopes? As we have shown before, exponentiating the estimate of the simple slope yields the odds ratio: \begin{align} OR_1 &= exp(slope_1) \\ log(OR_1) &= slope_1 \\ OR_2 &= exp(slope_2) \\ log(OR_2) &= slope_2 \end{align}
The quantities we are estimating above in the estimate statements are exponentiated differences of simple slopes, which is equivalent to exponentiating the difference between log-odds ratios:
$$exp(slope_2 – slope_1) = exp(log(OR_2)-log(OR_1))$$
Recalling our logarithmic identity again: $$logA-logB = log\frac{A}{B}$$
We then get: $$exp(slope_2 – slope_1) = exp(log(\frac{OR_2}{OR_1}))$$ $$exp(slope_2 – slope_1) = \frac{OR_2}{OR_1}$$
The exponentiated difference between simple slopes thus expresses the ratio between two odds ratios, or a ratios of odds ratios (ROR). In other words, the exponentiated difference express by what factor 2 odds ratios differ — an ROR greater than 1 expresses that effect in the numerator increases the odds of the outcome by a greater factor (by a greater percent change) than the effect in the numerator. For example, in the previous section, we calculated the OR for hours in the jogging program as 4.1, and the OR for hours in the swimming program as 5.1. The ratio of these 2 ORs is \(4.1/5.1 = .8\), which is the exponentiated estimate in the first row above. Because the ROR=.8 is less than 1, we know that increasing the number of hours increases the odds of the outcome by a smaller factor in the jogging program (numerator) than in the swimming program.
7.5 Logistic regression, categorical-by-continuous interaction: simple effects analysis and predicted probabilities
We might also be intereseted in the simple effects of program at different numbers of hours exercised. We an easily get our simple effects and an accompanying plot expressed as odds ratios using the oddsratio statement:
proc logistic data = exercise descending; class prog / param=glm order=internal; model satisfied = prog|hours / expb; oddsratio prog / at(hours = 1.51 2 2.5); store logit; run;
| Odds Ratio Estimates and Wald Confidence Intervals | |||
|---|---|---|---|
| Odds Ratio | Estimate | 95% Confidence Limits | |
| prog jogging vs swimming at hours=1.51 | 0.601 | 0.345 | 1.048 |
| prog jogging vs reading at hours=1.51 | 0.220 | 0.130 | 0.370 |
| prog swimming vs reading at hours=1.51 | 0.365 | 0.224 | 0.597 |
| prog jogging vs swimming at hours=2 | 0.542 | 0.382 | 0.769 |
| prog jogging vs reading at hours=2 | 0.512 | 0.364 | 0.721 |
| prog swimming vs reading at hours=2 | 0.946 | 0.679 | 1.317 |
| prog jogging vs swimming at hours=2.5 | 0.487 | 0.291 | 0.816 |
| prog jogging vs reading at hours=2.5 | 1.216 | 0.764 | 1.937 |
| prog swimming vs reading at hours=2.5 | 2.496 | 1.536 | 4.054 |
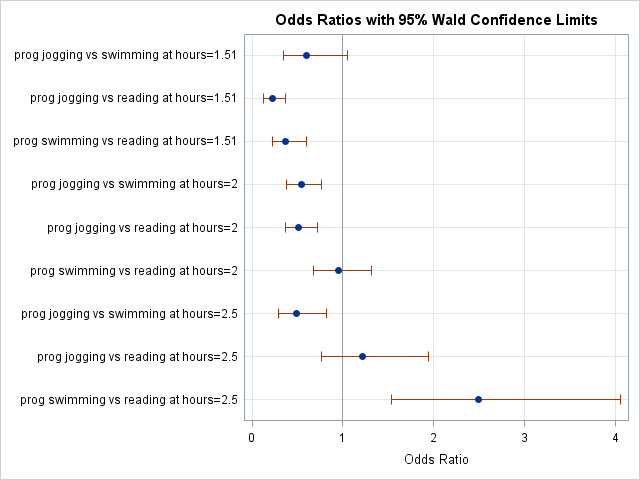
From the table and graph, it appears that at the lower number of hours of 1.51, subjects are more likely to be satisfied in the reading program than the other 2. However, as the number of hours increases to 2.5, subjects are more likely to be satisfied in the swimming program than the other 2.
Odds ratios are certainly informative, but they can be misleading because we do not know what are the probabilities underlying these odds ratios (see section 7.1 above). We thus recommend that researchers estimate probabilities of the outcome across various values of the predictors to give these odds ratios more meaning.
Predicted probabilities across various levels of the predictor are most easily obtained through the lsmeans statement, which is related to both the slice and the lsmestimate statement we have introduced already.
Notice in the code below:
- We specify “prog” after the
lsmeanskeyword – which tells SAS to estimate means at each level of prog. - We specify the value of hours at which to calculate these means using the
atoption. Predictors in the model not specified after the keywordlsmeansstatement will be fixed by default at their means, if continuous, or if the predictor is categorical, the mean is averaged over all categories as if they were balanced (hence the “balanced population”). - We specify the
ilinkoption to request that means also be calculated and reported in the original metric (probabilities) rather than just in the transformed metric, here log-odds (logits). - We suppress the default plots produced by
lsmeans, as they take quite a bit of time to produce and are hard to interpret for many users
proc plm source = logit; lsmeans prog / at hours=1.51 ilink plots=none; lsmeans prog / at hours=2 ilink plots=none; lsmeans prog / at hours=2.5 ilink plots=none; run;
| prog Least Squares Means | |||||||
|---|---|---|---|---|---|---|---|
| prog | hours | Estimate | Standard Error | z Value | Pr > |z| | Mean | Standard Error of Mean |
| jogging | 1.51 | -1.4185 | 0.2101 | -6.75 | <.0001 | 0.1949 | 0.03296 |
| swimming | 1.51 | -0.9094 | 0.1908 | -4.77 | <.0001 | 0.2871 | 0.03905 |
| reading | 1.51 | 0.09735 | 0.1628 | 0.60 | 0.5499 | 0.5243 | 0.04060 |
| prog Least Squares Means | |||||||
|---|---|---|---|---|---|---|---|
| prog | hours | Estimate | Standard Error | z Value | Pr > |z| | Mean | Standard Error of Mean |
| jogging | 2.00 | -0.7261 | 0.1295 | -5.61 | <.0001 | 0.3261 | 0.02846 |
| swimming | 2.00 | -0.1131 | 0.1230 | -0.92 | 0.3578 | 0.4718 | 0.03064 |
| reading | 2.00 | -0.05731 | 0.1161 | -0.49 | 0.6216 | 0.4857 | 0.02900 |
| prog Least Squares Means | |||||||
|---|---|---|---|---|---|---|---|
| prog | hours | Estimate | Standard Error | z Value | Pr > |z| | Mean | Standard Error of Mean |
| jogging | 2.50 | -0.01950 | 0.1792 | -0.11 | 0.9134 | 0.4951 | 0.04480 |
| swimming | 2.50 | 0.6994 | 0.1924 | 3.64 | 0.0003 | 0.6681 | 0.04266 |
| reading | 2.50 | -0.2151 | 0.1557 | -1.38 | 0.1671 | 0.4464 | 0.03848 |
In the above tables, the estimate in the transformed, log-odds metric is found in the “Estimate” column, while the estimate in the original probability metric is found in the “Mean” column. At the mean number of hours exercised (2), the probability of being satisified ranges from .33 to .49. At low numbers of hours (1.5), those in the reading program are more likely to be satisfied (.52 vs .19 and .29) while at a high number of hours (2.5), the swimming program is more likely to yield a satisfied subject (.67 vs .5 and .45).
Unfortunately, it is very difficult to get simple effects in logistic to be represented as differences in probabilities by SAS. You might think that we could use lsmeans, lsmestimate or slice statements with the ilink option to find the difference between predicted probabilities — but that will not work because ilink will back-transform at the wrong step. We can of course manually subtract predicted probabilities, but we get no standard error for this difference to use to test for signfiicance. If a standard error for the difference is really needed, we could perhaps boostrap the standard error.
Below, we provide two graphs of the predicted probabilities across programs and across a range of hours. In the first graph, we emphasize differences between the programs at 1.51, 2, and 2.5 weekly hours. In the second graph, we plot separate lines for each program across a continuous range of hours, which emphasizs the hours effect in each program. The default behavior of the effectplot statement in proc plm is to plot the untransformed response, here probabilities, so we do not need the ilink option.
proc plm restore=logit; effectplot interaction (x=prog) / at(hours = 1.51 2 2.5) clm; effectplot slicefit (x=hours sliceby=prog) / clm; run;
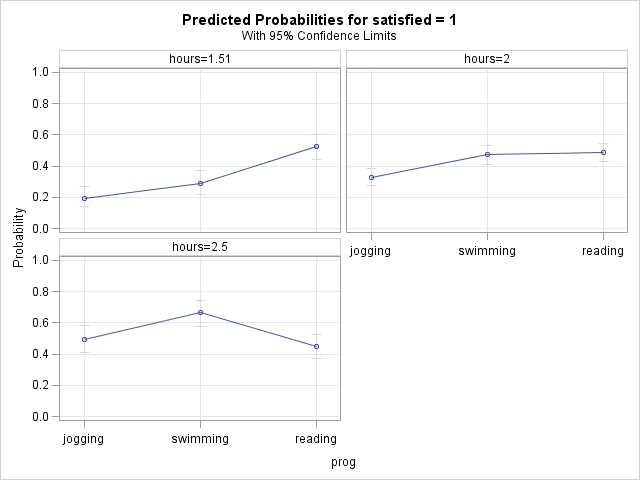
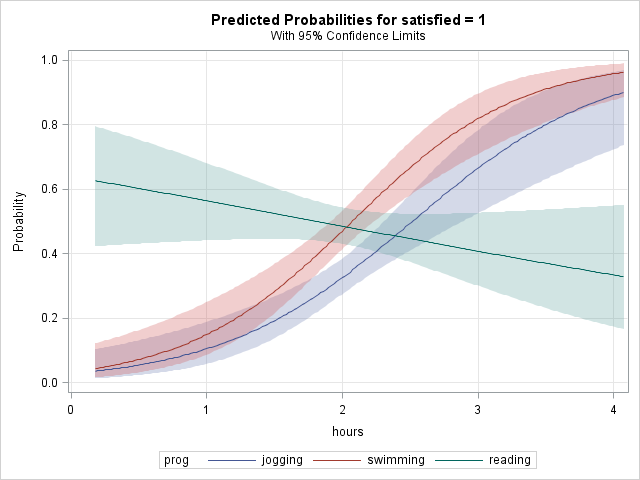
8. Conclusion: general guidelines for coding in proc plm
We find it generally easier to start with the lower order effects, or even estimated means, and then to build up to higher order effects by estimating differences between these lower order effects. For instance, in the analysis of simple effects, we might first start by estimating the cell means, then taking the differences between the cell means to get simple effects, and then taking differences between simple effects to test for interactions. Coding for lower order effects is typically more intuitively obvsious — it can be know exactly which terms are needed to test for an interaction.
Guidelines for estimating simple slopes using the estimate statement:
- Always put a value of 1 after the coefficient for the slope variable
- If the interacting variable is continuous (and not a quadratic effect), put the value of the interacting variable after the interaction coefficient (e.g.
estimate 'hours slope, effort=mean-sd' hours 1 hours*effort 24.52) - If the interacting variable is the IV itself (a quadratic effect), put the 2*value of the IV after the quadratic coefficient (e.g.
estimate 'hours slope, hours=mean-sd(1.5)' hours 1 hours*hours 3) - If the interacting variable is categorical, put a value of 1 after the interaction coefficient involving the group for whom the slope is being calculated. If the slope in the reference group is being estimated, a value of 1 is still needed for the interaction coefficient that is constrained to 0. (e.g.
estimate 'hours slope, prog=1 jogging' hours 1 hours*prog 1 0 0) - If the slope variable is involved in a 3-way interaction, make sure to specify values for the slope coefficient alone, all 2-way interaction coefficients involving both the slope and either of the 2 interacting variables, and the 3-way interaction coefficient involving all 3 variables. If the interaction (2-way or 3-way) coefficient involves only categorical moderators with the slope variable, apply a 1-value, and if the interaction coefficient involves a continuous moderator with the slope variable, apply the value of the continuous predictor (or double if it is a quadratic effect, or apply the product of 2 values if the 2 moderators are both continuous). (e.g
estimate 'hours slope, male prog=jogging' hours 1 hours*female 1 0 hours*prog 1 0 0 hours*female*prog 1 0 0 0 0 0) - To estimate differences between simple slopes, subtract values across coefficients.
- Use the
eoption to check that the values applied to the coefficients are correct - Use the
jointoption for joint F-tests. - Use the
adj=option to correct for multiple comparisons. - For logistic regression, use the
expoption to exponentiate simple slopes estimates so that they are expressed as odds ratios.
Guidelines for estimating simple effects using the lsmestimate statement:
- Think of simple effects as diffrences between means, and select a pair of means to compare
- Assign one mean the value 1 and the other -1.
- Remember to use ordinal values of categorical predictors to specify levels, not the actual level itself. For example, to specify the difference between the means for female=1,prog=1 and female=1,prog2, we want [1, 2 1] and [-1, 2 2] becuse female=1 is the second level of female (e.g lsmestimate female*prog ‘jogging-swimming, female = female(1)’ [1 2 1] [-1 2 2])
- To compare simple effects, reverse the values in one set of means corresponding to a simple effect (e.g
lsmestimate prog*female 'diff jogging-swimming, male - female' [1, 1 1] [-1, 1 2] [-1, 2 1] [1, 2 2]) - Use the
jointoption for joint F-tests. - Use the
adj=option to correct for multiple comparisons.
