Purpose
This seminar will show you how to decompose, probe, and plot two-way interactions in linear regression using the emmeans package in the R statistical programming language. For users of Stata, refer to Decomposing, Probing, and Plotting Interactions in Stata.
Outline
Throughout the seminar, we will be covering the following types of interactions:
- Continuous by continuous
- Continuous by categorical
- Categorical by categorical
We can probe or decompose each of these interactions by asking the following research questions:
- What is the predicted Y given a particular X and W? (predicted value)
- What is relationship of X on Y at particular values of W? (simple slopes/effects)
- Is there a difference in the relationship of X on Y for different values of W? (comparing simple slopes)
Proceed through the seminar in order or click on the hyperlinks below to go to a particular section:
- Main vs. Simple effects (slopes)
- Predicted Values vs. Slopes
- Continuous by Continuous
- Be wary of extrapolation
- Simple slopes for a continuous by continuous model
- Plotting a continuous by continuous interaction
- Testing simple slopes in a continuous by continuous model
- Testing differences in predicted values at a particular level of the moderator
- (Optional) Manually calculating the simple slopes
- (Optional) Creating a publication quality graph with ggplot
- Continuous by Categorical
- Categorical by Categorical
This seminar page was inspired by Analyzing and Visualizing Interactions in SAS. This page covers two way and three way interaction decompositions in the SAS programming language.
Requirements
Before beginning the seminar, please make sure you have R and RStudio installed.
Please also make sure to have the following R packages installed, and if not, run these commands in R (RStudio).
install.packages("emmeans", dependencies=TRUE)
install.packages("ggplot2", dependencies=TRUE)
The dataset used in the seminar can be found here: exercise.csv. You can also import the data directly into R via the URL using the following code:
dat <- read.csv("https://stats.idre.ucla.edu/wp-content/uploads/2019/03/exercise.csv")
Before you begin the seminar, load the data as above and convert gender and prog (exercise type) into factor variables:
dat$prog <- factor(dat$prog,labels=c("jog","swim","read"))
dat$gender <- factor(dat$gender,labels=c("male","female"))
Download the complete R code
You may download the complete R code here: interactions.r
After clicking on the link, you can copy and paste the entire code into R or RStudio.
Motivation
Suppose you are doing a simple study on weight loss and notice that people who spend more time exercising lose more weight. Upon further analysis you notice that those who spend the same amount of time exercising lose more weight if they are more effortful. The more effort people put into their workouts, the less time they need to spend exercising. This is popular in workouts like high intensity interval training (HIIT).
You know that hours spent exercising improves weight loss, but how does it interact with effort? Here are three questions you can ask based on hypothetical scenarios.
- I’m just starting out and don’t want to put in too much effort. How many hours per week of exercise do I need to put in to lose 5 pounds?
- I’m moderately fit and can put in an average level of effort into my workout. For every one hour increase per week in exercise, how much additional weight loss do I expect?
- I’m a crossfit athlete and can perform with the utmost intensity. How much more weight loss would I expect for every one hour increase in exercise compared to the average amount of effort most people put in?
Additionally, we can visualize the interaction to help us understand these relationships.
Weight Loss Study
This is a hypothetical study of weight loss for 900 participants in a year-long study of 3 different exercise programs, a jogging program, a swimming program, and a reading program which serves as a control activity. Variables include
loss: weight loss (continuous), positive = weight loss, negative scores = weight gain
hours: hours spent exercising (continuous)
effort: effort during exercise (continuous), 0 = minimal physical effort and 50 = maximum effort
prog: exercise program (categorical)
- jogging=1
- swimming=2
- reading=3
gender: participant gender (binary)
- male=1
- female=2
Definitions
What exactly do I mean by decomposing, probing, and plotting an interaction?
- decompose: to break down the interaction into its lower order components (i.e., predicted means or simple slopes)
- probe: to use hypothesis testing to assess the statistical significance of simple slopes and simple slope differences (i.e., interactions)
- plot: to visually display the interaction in the form of simple slopes such as values of the dependent variable are on the y-axis, values of the predictor is on the x-axis, and the moderator separates the lines or bar graphs
Let’s define the essential elements of the interaction in a regression:
- DV: dependent variable (Y), the outcome of your study (e.g., weight loss)
- IV: independent variable (X), the predictor of your outcome (e.g., time exercising)
- MV: moderating variable (W) or moderator, a predictor that changes the relationship of the IV on the DV (e.g, effort)
- coefficient: estimate of the direction and magnitude of the relationship between an IV and DV
- continuous variable: a variable that can be measured on a continuous scale, e.g., weight, height
- categorical or binary variable: a variable that takes on discrete values, binary variables take on exactly two values, categorical variables can take on 3 or more values (e.g., gender, ethnicity)
- main effects or slopes: effects or slopes for models that do not involve interaction terms
- simple slope: when a continuous IV interacts with an MV, its slope at a particular level of an MV
- simple effect: when a categorical IV interacts with an MV, its effect at a particular level of an MV
Main vs. Simple effects (slopes)
Let’s do a brief review of multiple regression. Suppose you have an outcome $Y$, and two continuous independent variables $X$ and $W$.
$$\hat{Y}= b_0 + b_1 X + b_2 W$$
We can interpret the coefficients as follows:
- $b_0$: the intercept, or the predicted outcome when $X=0$ and $W=0$.
- $b_1$: the slope (or main effect) of $X$; for a one unit change in $X$ the predicted change in $Y$
- $b_2$: the slope (or main effect) of $W$; for a one unit change in $W$ the predicted change in $Y$
Here only the intercept is interpreted at zero values of the IV’s. For a more thorough explanation of multiple regression look at Section 1.5 of the seminar Introduction to Regression with SPSS.
Interactions are formed by the product of any two variables.
$$\hat{Y}= b_0 + b_1 X + b_2 W + b_3 X*W$$
Each coefficient is interpreted as:
- $b_0$: the intercept, or the predicted outcome when $X=0$ and $W=0$.
- $b_1$: the simple effect or slope of $X$, for a one unit change in $X$ the predicted change in $Y$ at $W=0$
- $b_2$: the simple effect or slope of $W$, for a one unit change in $W$ the predicted change in $Y$ at $X=0$
- $b_3$: the interaction of $X$ and $W$, the change in the slope of $X$ for a one unit increase in $W$ (or vice versa)
For an interaction model, not only is the intercept fixed at 0 of $X$ and $W$, but each coefficient of an IV interacted with an MV is interpreted at zero of the MV. We say that the effect $X$ varies by levels of $W$ (and identically, that the effect $W$ varies by levels of $X$). Focusing on $X$ as our IV and $W$ as our MV, with a rearrangement of the terms in our model,
$$\hat{Y}= b_0 + b_2 W + (b_1+b_3 W)X$$
we can see that the coefficient for $X$ is now $b_1+b_3 W$, which means the coefficient of $X$ is a function of $W$. For example, if $W=0$ then the slope of $X$ is $b_1$; but if $W=1$, the slope of $X$ is $b_1+b_3$. The coefficient $b_3$ is thus the additional increase in the effect or slope of $X$ as $W$ increases by one unit.
Predicted Values vs. Slopes
After fitting a regression model, we are often interested in the predicted mean given a fixed value of the IV’s or MV’s. For example, suppose we want to know the predicted weight loss after putting in two hours of exercise. We fit the main effects model,
$$\hat{\mbox{WeightLoss}}= b_0 + b_1 \mbox{Hours}.$$
Using the function lm, we specify the following syntax:
cont <- lm(loss~hours,data=dat) summary(cont)
and obtain the following summary table:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.0757 1.9550 2.596 0.00958 **
hours 2.4696 0.9479 2.605 0.00933 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
In equation form, we get
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47 \mbox{Hours}.$$
We can plug in $\mbox{Hours}=2$ to get
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47 (2) = 10.02.$$
The predicted weight loss is 10.02 pounds from 2 hours of exercise (remember, this is a hypothetical study). This is an example that we can work by hand, but we can also ask emmeans to help us.
The package emmeans (written by Lenth et. al at the University of Iowa) is a suite of post-estimation functions to obtain marginal means, predicted values and simple slopes. Post-estimation means that you must run a type of linear model before running emmeans by first storing the lm object and then passing this object into emmeans. In our example, we are requesting predicted values withemmeans. To do so, we need to store particular values of our predictor, Hours = 2, into an R list called mylist.
(mylist <- list(hours=2))
Then we will pass mylist into emmeans, which will help use get the predicted value of weight loss at Hours=2.
> emmeans(cont, ~ hours, at=mylist)
hours emmean SE df lower.CL upper.CL
2 10 0.469 898 9.1 10.9
Confidence level used: 0.95
We get a predicted value of 10, which matches our computed value of 10.02 (rounded to the single digit). Losing 10 pounds of weight for 2 hours of exercise seems a little unrealistic. Maybe this study was conducted on the moon.
Understanding slopes in regression
Now that we understand predicted values how do you obtain a slope? Well a slope is defined as
$$ m = \frac{\mbox{change in } Y }{\mbox{change in } X } =\frac{\Delta Y }{\Delta X } $$
where $\Delta Y = y_2 – y_1$ and $\Delta X = x_2 – x_1 $. In regression, we usually talk about a one-unit change in $X$ so that $\Delta X = 1 – 0 = 1 $. This makes our slope formula simply $$ m = \Delta Y.$$ So how do we find our slope? Going back to our original equation,
$$\hat{\mbox{WeightLoss}}= 5.08 + 2.47 \mbox{Hours}. $$
We can interpret the $b_1 = 2.47$ as a slope, as $b_1$ is interpreted as the change in $Y$ for a one unit change in $X$. In our case, for a one hour increase in time put in, we achieve 2.47 pounds of weight loss. In fact, we can derive the slope by obtaining two predicted values, one for Hours =0 and another for Hours =1. The symbol “|” means given, which means holding a variable at a particular value. Plugging in $X=0$ into our original regression equation,
$$\hat{\mbox{WeightLoss}} | _{\mbox{Hours}= 0} = 5.08 + 2.47 (0) = 5.08.$$ Similarly, we can predict weight loss for Hours = 1 $$\hat{\mbox{WeightLoss}} | _{\mbox{Hours} = 1} = 5.08 + 2.47 (1) = 7.55.$$
Now we have $y_2 = 7.55$ and $y_1 =5.08$, using our slope formula $m = 7.55 -5.08 = 2.47$. We obtain 2.47, which equals our value of $b_1.$ This means that $b_1$ is in fact the slope of Hours, given a one hour change. Of course we can easily obtain the slope using summary(cont), but for edification purposes, let’s see how we can obtain this using our package emmeans. Recall that we’ve already stored our lm object into cont. However, instead of using the function emmeans, we use another function specially made for calculating slopes called emtrends.
> emtrends(cont, ~ 1, var="hours") 1 hours.trend SE df lower.CL upper.CL overall 2.47 0.948 898 0.609 4.33 Confidence level used: 0.95
We are telling emtrends to recall the lm object cont. The ~ 1 tells the function to obtain the overall slope and var="hours" tells the function that we want the slope for the variable Hours. You can easily change the level of Hours, but because this is a main effects model, the slope does not change. Remember that the slopes only change when we interact one IV with an MV, as we will see in the following example.
Quiz: (True or False) emtrends is used to estimate predicted values and emmeans is used to estimate simple slopes.
Answer: False, emtrends estimates simple slopes.
Exercise
Predict two values of weight loss for Hours = 10 and Hours = 20 using emmeans, then calculate the slope by hand. How do the results compare with emtrends?
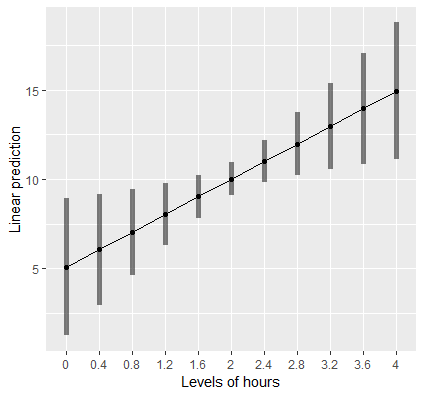
Plotting a regression slope
Visualizing is always a good thing. Let’s suppose we want to create a plot of the relationship of Hours and Weight Loss. The function emmip allows us to easily plot this. First however, we have to create a new list of values of Hours so that we have enough points on the x-axis to create a line.
> (mylist <- list(hours=seq(0,4,by=0.4))) $hours [1] 0.0 0.4 0.8 1.2 1.6 2.0 2.4 2.8 3.2 3.6 4.0
This code creates a sequence of numbers from 0 to 4, incremented by 0.4 each. We can now pass this list into the function emmip as follows:
emmip(cont,~hours,at=mylist, CIs=TRUE)
First, we pass in our object cont as before, and specify after the ~ that we want Hours on the x-axis. The at=mylist tells the function that we want the plot to generate a tick on the x-axis at each value in the sequenced list of numbers. Finally CIs=TRUE requests confidence intervals. In the next section we will discuss how to estimate and interpret slopes that vary with levels of another variable as well as produce professional looking plots with ggplot.
Continuous by Continuous
We know that amount of exercise is positively related with weight loss. Given the recent news about the efficacy of high intensity interval training (HIIT), perhaps we can achieve the same weight loss goals in a shorter time interval if we increase our exercise intensity. The question we ask is does effort (W) moderate the relationship of Hours (X) on Weight Loss (Y)? The model to address the research question is
$$\hat{\mbox{WeightLoss}}= b_0 + b_1 \mbox{Hours} + b_2 \mbox{Effort} + b_3 \mbox{Hours*Effort}.$$
We can fit this in R with the following code:
contcont <- lm(loss~hours*effort,data=dat) summary(contcont)
The lm code with just the interaction term indicated by a star is equivalent to adding the lower order terms to the interaction term specified by a colon:
contcont <- lm(loss ~ hours + effort + hours:effort, data=dat)
Obtain the following shortened output:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.79864 11.60362 0.672 0.5017
hours -9.37568 5.66392 -1.655 0.0982 .
effort -0.08028 0.38465 -0.209 0.8347
hours:effort 0.39335 0.18750 2.098 0.0362 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The interaction Hours*Effort is significant, which suggests that the relationship of Hours on Weight loss varies by levels of Effort. Before decomposing the interaction let’s interpret each of the coefficients.
- $b_0$
(Intercept): the intercept, or the predicted outcome when Hours = 0 and Effort = 0. - $b_1$
hours: the simple slope of Hours, for a one unit change in Hours, the predicted change in weight loss at Effort=0. - $b_2$
effort: the simple slope of Effort, for a one unit change in Effort the predicted change in weight loss at Hours=0. - $b_3$
hours:effort: the interaction of Hours and Effort, the change in the slope of Hours for every one unit increase in Effort (or vice versa).
Before proceeding, let’s discuss our findings for $b_1$. Although we may think that the slope of Hours should be positive at levels of Effort, remember that in this case, Effort is zero. As we see in our data, this is improbable as the minimum value of effort is 12.95.
> summary(dat$effort) Min. 1st Qu. Median Mean 3rd Qu. Max. 12.95 26.26 29.63 29.66 33.10 44.08
Be wary of extrapolation
Suppose we want to find the predicted weight loss given two hours of exercise and an effort of 30. As before, we create a list that takes on a value of 2 for Hours and 30 for Effort:
(mylist <- list(hours=2,effort=30)) emmeans(contcont, ~ hours*effort, at=mylist)
The output we obtain is:
hours effort emmean SE df lower.CL upper.CL
2 30 10.2 0.453 896 9.35 11.1
Confidence level used: 0.95
The results show that predicted weight loss is 10.2 pounds if we put in two hours of exercise and an effort level of 30; this seems reasonable. Let’s see what happens when we predict weight loss for two hours of exercise given an effort level of 0.
> mylist <- list(hours=2,effort=0)
> emmeans(contcont, ~ hours*effort, at=mylist)
hours effort emmean SE df lower.CL upper.CL
2 0 -11 2.65 896 -16.1 -5.76
The predicted weight gain is now 11 pounds. This is demonstration of the fact that we are extrapolating, which means we are making predictions about our data beyond what the data can support. This is why we should always choose reasonable values of our predictors in order to interpret our data properly.
In order to achieve plausible values, some researchers may choose to do what is known as centering, which is subtracting a constant $c$ from the variable so that $X^{*} = X-c$. Since $X^{*} = 0$ implies $X=c$, the intercept, simple slopes and simple effects are interpreted at $X=c$. A popular constant is $c=\bar{x}$, so that all intercepts, simple slopes and simple effects are interpreted at the mean of $X$. Extrapolation then becomes a non-issue.
Simple slopes for a continuous by continuous model
We know to choose reasonable values when predicting values. The same concept applies when decomposing an interaction. Our output suggests that Hours varies by levels of Effort. Since effort is continuous, we can choose an infinite set of values with which to fix effort. For ease of presentation, some researchers pick three representative values of Effort with which to estimate the slope of Hours. This is often known as spotlight analysis, which was made popular by Leona Aiken and Stephen West’s book Multiple Regression: Testing and Interpreting Interactions (1991). Traditional spotlight analysis was made for a continuous by categorical variable but we will borrow the same concept here. What three values should we choose? Aiken and West recommend plotting three lines for Hours, one at the mean level of Effort, a second at one standard deviation about the mean level of Effort, and finally a third at one standard deviation below the mean level of effort. In symbols, we have
$$ \begin{eqnarray} \mbox{EffA} & = & \overline{\mbox{Effort}} + \sigma({\mbox{Effort}}) \\ \mbox{Eff} & = & \overline{\mbox{Effort}} \\ \mbox{EffB} & = & \overline{\mbox{Effort}} – \sigma({\mbox{Effort}}). \end{eqnarray} $$
In R, we can use the following, by using the functions mean and sd to obtain the mean and standard deviation of our effort variable, storing the “low”, “medium” and “high” values of effort into separate objects.
effa <- mean(dat$effort) + sd(dat$effort) eff <- mean(dat$effort) effb <- mean(dat$effort) - sd(dat$effort)
For ease of presentation, let’s round our values to the tens digit and store each object as a new object with the tag r.
> (effar <- round(effa,1)) [1] 34.8 > (effr <- round(eff,1)) [1] 29.7 > (effbr <- round(effb,1)) [1] 24.5
The mean of effort is about 30. A quick way to check the values of one standard deviation above and one standard deviation below is to make sure that the former (34.8) is higher than the latter (24.5).
Recall that our simple slope is the relationship of hours on weight loss fixed a particular values of effort. In R, we can obtain simple slopes using the function emtrends. We first create a list which incorporates the three values of effort we found above in preparation for spotlight analysis.
> mylist <- list(effort=c(effbr,effr,effar)) > emtrends(contcont, ~effort, var="hours",at=mylist) effort hours.trend SE df lower.CL upper.CL 24.5 0.261 1.352 896 -2.392 2.91 29.7 2.307 0.915 896 0.511 4.10 34.8 4.313 1.308 896 1.745 6.88 Confidence level used: 0.95
First, store the three values of effort, “low”, “medium” and “high” into mylist. Then call emtrends and pass contcont into our function as our lm object from our continuous by continuous interaction model. Specify~effort to tell the function to obtain separate estimates for each level of effort, var="hours" to tell the function which trend (simple slope) to obtain and finally at=mylist to specify specific levels of Effort (here it’s 24.5, 29.7 and 34.8). We get three separate (simple) slopes for hours. As we increase levels of Effort, the relationship of hours on weight loss seems to increase. There is no test of the slopes, but we can look at the lower.CL and upper.CL to see if the 95% confidence interval contains zero. If it the interval contains zero, then the simple slope is not significant. Here it seems that the simple slope of Hours is significant only for mean Effort levels and above. Finally, the degrees of freedom df is 896 because we have a sample size of 900, 3 predictors and 1 intercept, $df= n-p-1 = 900-3-1=896.$ Let’s see what these three simple slopes look like visually.
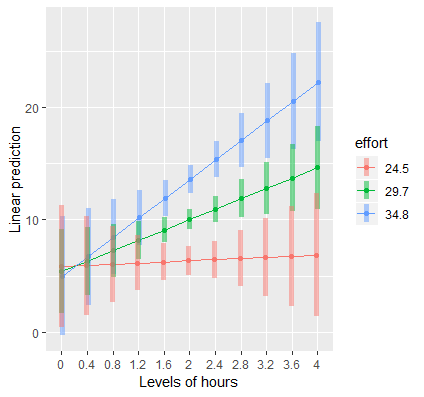
Plotting a continuous by continuous interaction
In order to plot our interaction, we want the IV (Hours) to be on the x-axis and the MV (Effort) to separate the lines. For the x-axis, we need to create a sequence of values to span a reasonable range of Hours, but we need only three values of Effort for spotlight analysis. First we create a list where Hours is now a sequence of values from 0 to 4, incremented by 0.4 and Effort is assigned one standard deviation below the mean, at the mean and one standard deviation above the mean. The code and output is listed below. We advise checking the output to confirm whether you specified the list correctly.
> (mylist <- list(hours=seq(0,4,by=0.4),effort=c(effbr,effr,effar))) $hours [1] 0.0 0.4 0.8 1.2 1.6 2.0 2.4 2.8 3.2 3.6 4.0 $effort [1] 24.5 29.7 34.8
From here we are ready to use emmip to plot. Pass the lm object contcont into the function and specify effort~hours to plot hours on the x-axis and separated by effort, fixed at=mylist. Finally, we request CIs=TRUE to request confidence bands.
emmip(contcont,effort~hours,at=mylist, CIs=TRUE)
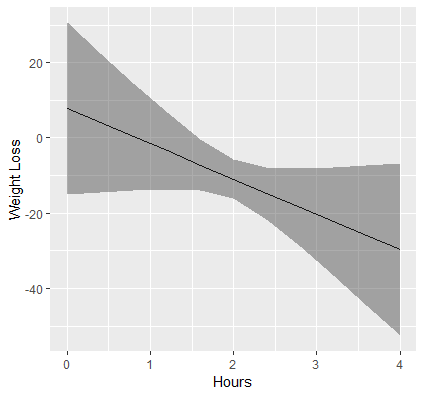
Here is the plot we obtain:
Just as we observed from emtrends, the simple slope of Hours at “low” effort is flat, but is positive for “medium” effort and above. The results suggest that hours spent exercising is only effective for weight loss if we put in more effort, which supports the rationale for high intensity interval training. At the highest levels of Effort, we achieve higher weight loss for a given time input.
Testing simple slopes in a continuous by continuous model
Looking at the graph, we may think that only the slope of “low” effort is significantly different from the others. Let’s confirm if this is true with the following syntax:
emtrends(contcont, pairwise ~effort, var="hours",at=mylist, adjust="none")
The syntax pairwise ~effort tells the function that we want pairwise differences of the simple slopes of var="hours" for each level of effort specified at=mylist. Finally the default p-value adjustment method is Tukey which controls for Type I error, but here we turn it off and use adjust="none".
The output we obtain is as follows:
$contrasts contrast estimate SE df t.ratio p.value 24.5 - 29.7 -2.05 0.975 896 -2.098 0.0362 24.5 - 34.8 -4.05 1.931 896 -2.098 0.0362 29.7 - 34.8 -2.01 0.956 896 -2.098 0.0362 Results are averaged over the levels of: hours
We can see that all the p-values for all three pairwise comparisons are the same. Furthermore, this p-value matches that of the interaction term in summary(contcont):
Coefficients:
Estimate Std. Error t value Pr(>|t|)
hours:effort 0.39335 0.18750 2.098 0.0362 *
This is not a coincidence because for a continuous by continuous interaction, all comparisons of simple slopes result in the same p-value as the interaction itself (we will not go into detail about why, but it has to do with the slope formula from above and the fact that we divide the change in Y by a proportional change in X). Back to our intuition that the slopes for the “low” effort group is lower than that of “medium” or “high” group. Based on the tests above, yes the maginitue of the slope is larger between “low” and “high” versus “medium” and “high”, but the two p-values are the same.
Testing differences in predicted values at a particular level of the moderator
Although the p-values of the difference in the Hours slopes are identical across levels of the effort in a continuous by continuous interaction, it may be that the predicted value of hours differs by levels of Effort. From the plot, we may assume that for a person who has exercised for four hours, there is a a difference in predicted weight loss at low effort (one SD below) versus high effort (one SD above).
In order to test this, we need to generate a new list where hours=4, and effort is only specified at the low and high levels (look back at the predicted values section). Now we are no longer testing simple slopes but predicted values, so we invoke emmeans not emtrends. We specify pairwise ~ hours*effort to tell the function that we want pairwise contrasts of each distinct combination of Hours and Effort specified at=mylist.
(mylist <- list(hours=4,effort=c(effbr,effar))) emmeans(contcont, pairwise ~ hours*effort, at=mylist)
The output we obtain is as follows
$emmeans
hours effort emmean SE df lower.CL upper.CL
4 24.5 6.88 2.79 896 1.4 12.4
4 34.8 22.26 2.68 896 17.0 27.5
Confidence level used: 0.95
$contrasts
contrast estimate SE df t.ratio p.value
4,24.5 - 4,34.8 -15.4 3.97 896 -3.871 0.0001
We check that our list was correctly specified at Hour=4 and Effort at low and high levels, which results in 6.88 and 22.26 respectively. From the pairwise contrast we verify that 6.88-22.26 = -15.38, and the p-value indicates that it is significant, verifying our observations from the graph that for 4 hours of exercise, high effort will result in 15 pounds more weight loss than low effort.
(Optional) Manually calculating the simple slopes
Recall that for a continuous by continuous interaction model we can re-arrange the equation such that
$$\hat{Y}= b_0 + b_2 W + (b_1+b_3 W)X.$$
Rerranging the terms allows you to obtain a new simple slope of $X$ defined as $(b_1+b_3 W)X$, which means that the slope of $X$ depends on values of $W$. Let’s see how we can derive the simple slope by hand (without calculus).
First, we consider the definition of the simple slope of $X$, which is defined as the slope of $X$ for a fixed value of $W=w$. Recall that the slope (which we call $m$) is the change in $Y$ over the change in $X$,
$$ m = \frac{\mbox{change in } Y }{\mbox{change in } X } =\frac{\Delta Y }{\Delta X }.$$
To simplify our notation, we consider our model before fitting it with the data (to eliminate the hat symbol). Let $\Delta {Y} = Y|_{X=1, W=w} – Y|_{X=0, W=w}$ and $\Delta {X} = X_1 – X_0.$ In regression we consider a one unit change in $X$ so $\Delta {X}=1.$ Then the slope $m$ depends only on the change in $Y$. Since a simple slope depends on levels of $W$, $m_{W=w}$ means we calculate the slope at a fixed constant $w$. Let’s calculate two simple slopes, $m_{W=0}$ and $m_{W=1}$,
$$ \begin{eqnarray} m_{W=1} & = & Y|_{X=1, W=1} – Y|_{X=0, W=1} \\ m_{W=0} & = & Y|_{X=1, W=0} – Y|_{X=0, W=0}. \end{eqnarray} $$
Each $Y$ is a predicted value, for a given $X=x$ and $W=w$. Simply plug in each value into our original interaction model,
$$ \begin{eqnarray} Y|_{X=1, W=1} &=& b_0 + b_1 (X=1) + b_2 (W=1) + b_3 (X=1)*(W=1) &=& b_0 + b_1 + b_2 + b_3\\ Y|_{X=0, W=1} &=& b_0 + b_1 (X=0) + b_2 (W=1) + b_3 (X=0)*(W=1) &=& b_0 + b_2 \\ Y|_{X=1, W=0} &=& b_0 + b_1 (X=1) + b_2 (W=0) + b_3 (X=1)*(W=0) &=& b_0 + b_1 \\ Y|_{X=0, W=0} &=& b_0 + b_1 (X=0) + b_2 (W=0) + b_3 (X=0)*(W=0) &=& b_0. \end{eqnarray} $$
Substituting these four equations back into the simple slopes we get:
$$ \begin{eqnarray} m_{W=1} & = & Y|_{X=1, W=1} – Y|_{X=0, W=1} & = & (b_0 + b_1 + b_2 + b_3) – (b_0 + b_2) & = & b_1 + b_3 \\ m_{W=0} & = & Y|_{X=1, W=0} – Y|_{X=0, W=0} & = & (b_0 + b_1) – (b_0) &=& b_1. \end{eqnarray} $$
Now consider our simple slope formula $(b_1+b_3 W)X$. If we plug in $W=1$ we obtain $b_1+b_3$ which equals $m_{W=1}$ and if you plug in $W=0$ we obtain $b_1$ which equals $m_{W=0}$. Isn’t math beautiful?
Finally, to get the interaction for a continuous by continuous interaction, take the difference in the simple slope of $m_{W=1}$ and $m_{W=0}$ (you can take any one unit change in $W$ to get the same simple slope). Therefore $m_{W=1}-m_{W=0}= (b_1 + b_3) – (b_1) = b_3$ which is exactly the same as the interaction coefficient $b_3$.
Exercise
The following exercise will guide you through deriving the interaction term using predicted values.
- Obtain predicted values for the following values and store the results into objects p00, p10, p01,p11
- Hours = 0, Effort = 0 (p00)
- Hours = 1, Effort = 0 (p10)
- Hours = 0, Effort = 1 (p01)
- Hours = 1, Effort = 1 (p11)
To help you with the coding, the equations are provided below. You can also manually calculate the predicted values to aid understanding.
\begin{eqnarray} p_{00} &=& 7.80 + (-9.38) \mbox{(Hours=0)} + (-0.08) \mbox{(Effort=0)} + (0.393) \mbox{(Hours=0)*(Effort=0)} \\ p_{10} &=& 7.80 + (-9.38) \mbox{(Hours=1)} + (-0.08) \mbox{(Effort=0)} + (0.393) \mbox{(Hours=1)*(Effort=0)} \\ p_{01} &=& 7.80 + (-9.38) \mbox{(Hours=0)} + (-0.08) \mbox{(Effort=1)} + (0.393) \mbox{(Hours=0)*(Effort=1)} \\ p_{11} &=& 7.80 + (-9.38) \mbox{(Hours=1)} + (-0.08) \mbox{(Effort=1)} + (0.393) \mbox{(Hours=1)*(Effort=1)} \end{eqnarray}
- Store the four predicted values (p00, p10, p01, and p11) into corresponding objects y00, y10, y01, and y11 by invoking
summary(p##)$emmean.- For example,
k1 <- summary(p00)$emmean
- For example,
- Take the following differences. What coefficients do these difference correspond to in
summary(contcont)? (Hint: one of the differences is a sum of two coefficients)- y10 – y00
- y11 – y01
- Take the difference of the two differences in Step 3. Which coefficient does this correspond to in
summary(contcont)?
Answers: 2) y00 = 7.80, y10 = -1.58, y01 = 7.72, y11 = -1.26; 3) y10 – y00 is $b_1=-9.38$, the simple slope of Hours at Effort = 0; y11 – y01 is $b_1+b_3 = -8.98$, the simple slope of Hours at Effort = 1; 4) $b_3=0.394$ is the interaction.
(Optional) Creating a publication quality graph with ggplot
Although you can easily plot your continuous by continuous graph with emmip, often times we would like to customize our graphs to prepare it for publication. The package ggplot2 created by Hadley Wickham is an simple to use and elegant graphing system based on what is known as The Grammar of Graphics. We will not go into detail here, but you can refer to our seminar Introduction to ggplot2 if you want more exposure to the topic.
From our previous example recall that we used emmip to create the plot. This function can also be used to simply output a set of values using plotit=FALSE. For example, let’s suppose we want to create a plot again with hours on the x-axis ranging from 0 to 4 and our three values of effort. Again we create a list just as before and pass the list into emmip.
(mylist <- list(hours=seq(0,4,by=0.4),effort=c(effbr,effr,effar))) contcontdat <- emmip(contcont,effort~hours,at=mylist, CIs=TRUE, plotit=FALSE)
The code is exactly the same as the code we used before except we add plotit=FALSE to tell the function not to output the graph but to output a data frame contain the predicted values we requested. Then store this data frame into object contcontdat. Here are some representative observations of this new data frame:
effort hours yvar SE df LCL UCL tvar xvar 1 24.5 0.0 5.831866 2.7679440 896 0.3994576 11.264275 24.5 0 10 24.5 1.2 6.145445 1.2473453 896 3.6973859 8.593503 24.5 1.2 33 34.8 4.0 22.256168 2.6838777 896 16.9887495 27.523587 34.8 4
The first column tells us the observation number, and effort and hours are familiar to us because we specified this in mylist. The last two columns are the same corresponding variables, except renamed to tvar and xvar for internal purposes. The new column yvar represents the predicted values of weight loss for every combination of the IV and MV, and SE and df represent the standard error and degrees of freedom. Columns LCL and UCL represent the lower and upper limits of the 95% confidence interval, which we will use to create our confidence bands.
Before we use ggplot, we need make sure that our moderator (effort) is a factor variable so that ggplot knows to plot separate lines. Additionally, it would help clarify our legend if we labeled our levels of Effort “low”, “med” and “high” to represent one SD below the mean, at the mean and one SD above the mean.
contcontdat$feffort <- factor(contcontdat$effort)
levels(contcontdat$feffort) <- c("low","med","high")
Now we are ready for ggplot. To break down the code a bit, let’s store each step into an object called p and then add a numeric value such as p1 to indicate the next sequence of code.
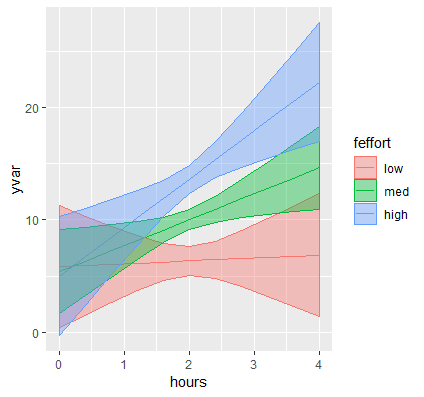
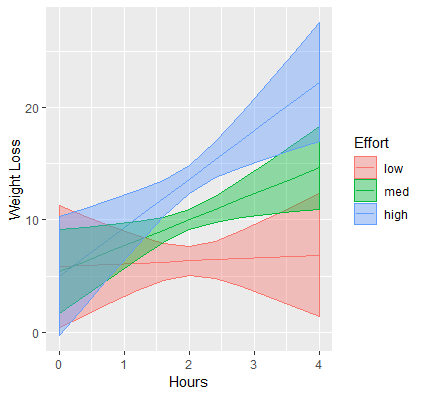
p <- ggplot(data=contcontdat, aes(x=hours,y=yvar, color=feffort)) + geom_line()
First, we call the function ggplot and pass in our data frame contcontdat. We assign Hours to the x-axis using x=hours and our predicted value for Weight Loss to the y-axis using y=yvars, and map the color aesthetic to different levels of Effort color = feffort (we use the factor version of effort and not the original variable). Finally, we connect each predicted value within a level of effort with geom_line(). The graph appears as below:
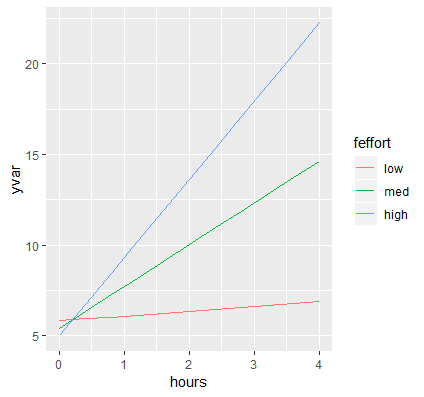
These are the simple slopes of hours for low, medium and high levels of Effort. Now let’s add the confidence bands, which can be accomplished by adding geom_ribbon to our previous graph. The function requires us to pass in the upper and lower limits of our predicted values, which we saw previously was UCL and LCL, specifying ymax=UCL, ymin=LCL. Instead of color which only colors the border of the ribbon, we want to map the aesthetic fill to each value of effort (its factor version) which fills in the ribbon by separate colors using fill=feffort within aes(). Finally, to prevent obfuscation of ribbons, we increase the transparency of the ribbons by adding alpha=0.4. You can decrease the alpha level to increase the transparency, the closer alpha is to zero, the more transparent it becomes.
p1 <- p + geom_ribbon(aes(ymax=UCL, ymin=LCL, fill=feffort), alpha=0.4)
Now that we have pretty ribbons, we add a final touch to our graph which is to change the labels of the x-axis, y-axis and legend to something more meaningful. Let’s label the x-axis “Hours”, the y-axis “Weight Loss” and the legend, which has two aesthetics color and fill to become “Effort”. If you only label one aesthetic and the label mismatches the second, you will create two separate legends which we do not want.
p1 + labs(x="Hours", y="Weight Loss", color="Effort", fill="Effort")
Our final publication quality graph is shown below:
In some circumstances it may be beneficial to use the continuous version of the continuous moderator, and in that case you would create a gradient of values instead of separate lines.
Exercise
Create a plot of hours on the x-axis with effort = 0 using ggplot, labeling the x-axis “Hours” and y-axis “Weight Loss”. The figure should look like the one below. Do the results seem plausible?
Continuous by Categorical
We know that exercise time positively relates to weight loss from prior studies but suppose we suspect gender differences in this relationship. The research question here is, do men and women (W) differ in the relationship between Hours (X) and Weight loss? This can be modeled by a continuous by categorical interaction where Gender is the moderator (MV) and Hours is the independent variable (IV). Before talking about the model, we have to introduce a new concept called dummy coding which is the default method of representing categorical variables in a regression model.
Suppose we only have two genders in our study, male and female. Dummy coding can be defined as
$$ D = \left\{ \begin{array}{ll} 1 & \mbox{if } X = x \\ 0 & \mbox{if } X \ne x \end{array} \right. $$
Let’s take the example of our variable gender, which can be represented by two dummy codes. The first dummy code $D_{female} = 1$ if $X= \mbox{Female}$, and $D_{female} = 0$ if $X= \mbox{Male}$. The second dummy code $D_{male}= 1$ if $X= \mbox{Male}$ and $D_{male}= 0$ if $X = \mbox{Female}$. The $k=2$ categories of Gender are represented by two dummy variables. However, only $k-1$ or 1 dummy code is needed to uniquely identify gender.
To see why only one dummy code is needed for a binary variable, suppose you have a female participant. Then for that particular participant, $D_{female} = 1$ which means we automatically know that she is not male, so $D_{male}=0$ (of course in the real world gender can be non-binary). If we entered both dummy variables into our regression, it would result in what is known as perfect collinearity (or redundancy) in our estimates and most statistical software programs would simply drop one of the dummy codes from your model.
Now we are ready to fit our model, recalling that we only enter one of the dummy codes. We have to be careful when choosing which dummy code to omit because the omitted group is also known as the reference group. We arbitrarily choose female to be the reference (or omitted) group which means we include the dummy code for males:
$$\hat{\mbox{WeightLoss}}= b_0 + b_1 \mbox{Hours} + b_2 D_{male}+ b_3 \mbox{Hours}*D_{male}$$
Quiz: What would the equation look like if we made males the reference group?
Answer: replace $D_{male}$ with $D_{female}$.
Before fitting this model into R, let’s do some data pre-processing. For categorical variables, there is a variable type known as a factor which will automatically generate dummy codes for the user. In our case, our factor variable is gender. We can verify that by the following:
> class(dat$gender) [1] "factor"
Factor variables in R have an attribute attached to them known as levels. Let’s see this in action by using the function levels:
> levels(dat$gender) [1] "male" "female"
Here we have two levels, male and female, and we know that the output of this command is a character vector with two elements, where Element 1 is male and Element 2 is female. The order of the elements is important for understanding dummy codes because R internally takes the first element and omits it from the model. This means that if we were to use gender in our lm model, R will take Element 1 from the character vector, which is “male”, and make that the omitted or reference group. Let’s confirm whether this is true:
catm <- lm(loss~gender,data=dat) summary(catm)
The (shortened) output we obtain is:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.1129 0.6650 15.206 <2e-16 ***
genderfemale -0.1842 0.9405 -0.196 0.845
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The naming of the variable genderfemale means that R is including the dummy code for females and omitting the dummy group for males.
Quiz: Write out the equation for the model above.
Answer: $\hat{\mbox{WeightLoss}}= b_0 + b_1 D_{female}$
Interpreting the coefficients of the continuous by categorical interaction
Now that we understand how R handles factor variables in lm models, we will go back to our original interaction model. In our original model we entered $D_{male}$ into our model which means we want to omit females. How would we do this in R? Since our original factor variable gender is leveled so that “male” is Element 1 and “female” is Element 2, we would need to reorder the levels of the factor variable such that the order is reversed. This can be accomplished by the function relevel:
> dat$gender <- relevel(dat$gender, ref="female") > levels(dat$gender) [1] "female" "male"
We re-level the original gender variable so that the reference group is now “female”. Internally, R is shifting the character vector so that “female” is now Element 1 and “male” is now Element 2. After re-leveling, we replace the re-coded gender into our data so that now female is our reference group. Using levels we see that “female” is now the first element in our character vector. Finally, we are ready to fit our original model into lm:
contcat <- lm(loss~hours*gender,data=dat) summary(contcat)
The shortened output we get is:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.335 2.731 1.221 0.222
hours 3.315 1.332 2.489 0.013 *
gendermale 3.571 3.915 0.912 0.362
hours:gendermale -1.724 1.898 -0.908 0.364
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The interaction Hours*Gender is not significant, which suggests that the relationship of Hours on Weight Loss does not vary by Gender. Before moving on, let’s interpret each of the coefficients.
- $b_0$
(Intercept): the intercept, or the predicted weight loss when Hours = 0 in the reference group of Gender, which is $D_{male}=0$ or females. - $b_1$
hours: the simple slope of Hours for the reference group $D_{male}=0$ or females. - $b_2$
gendermale: the simple effect of Gender or the difference in weight loss between males and females at Hours = 0. Recall that the naming convention R uses implies that males are included and females are omitted. - $b_3$
hours:gendermale: the interaction of Hours and Gender, the difference in the simple slopes of Hours for males versus females.
The most difficult term to interpret is $b_3$. Another way to think about it is if we know the slope of Hours for females, this is the additional slope for males. Since the Hours slope of females is $b_1$, the Hours slope of males is $b_1 + b_3$. The interaction is not significant, but we decide to probe the interaction anyway for demonstration purposes.
Obtaining simple slopes by each level of the categorical moderator
Since our goal is to obtain simple slopes of Hours by gender we use emtrends. We do not use emmeans because this function gives us the predicted values rather than slopes.
emtrends(contcat, ~ gender, var="hours")
We pass in contcat as our lm object from our continuous by categorical interaction model. The following parameters ~gender tells the function that we obtain separate estimates for females and males, and var="hours" tells the function to obtain simple slopes (or trends) for hours. The output we obtain is:
gender hours.trend SE df lower.CL upper.CL female 3.32 1.33 896 0.702 5.93 male 1.59 1.35 896 -1.063 4.25
The simple slope for females is 3.32, which is exactly the same as $b_1$ and males is 1.59 which is $b_1 + b_3 = 3.32 + (-1.72)$. The 95% confidence interval does not contain zero for females but contains zero for males, so the simple slope is significant for females but not for males.
A common misconception is that since the simple slope of Hours is significant for females but not males, we should have seen a significant interaction. However, the interaction tests the difference of the Hours slope for males and females and not whether each simple slope is different from zero (which is what we have from the output above).
Quiz: (True of False) If both simple slopes of Hours for males and females are significantly different from zero, it implies that the interaction of Hours*Gender is not significant.
Answer: False. The test of simple slopes is not the same as the test of the interaction, which tests the difference of simple slopes.
To test the difference in slopes, we add pairwise ~ gender to tell the function that we want the pairwise difference in the simple slope of Hours for females versus males.
emtrends(contcat, pairwise ~ gender, var="hours")
$contrasts contrast estimate SE df t.ratio p.value female - male 1.72 1.9 896 0.908 0.3639
What do we notice about the p-value and the estimate? Recall from our summary table, this is exactly the same as the interaction, which verifies that we have in fact obtained the interaction coefficient $b_3$. The only difference is that the sign is flipped because we are taking female – males (females have higher Hours slopes) whereas the interaction takes male – female. By default, pairwise emtrends takes all differences from the reference group. Take a look a the shortened summary table below and verify the p-value and the sign of the coefficient highlighted in red.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
hours:gendermale -1.724 1.898 -0.908 0.364
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Quiz: (True or False) Because we used $D_{male}$, the interaction term hours:gendermale takes males – females, whereas pairwise emtrends by default takes females – males.
Answer: True.
Quiz: (True of False) The parameter pairwise ~ gender, var="hours" tells emtrends that we want the simple effect of Gender split by levels of Hours.
Answer: False. We are not obtaining the simple effect of Gender but simple slopes of Hours. The statement var="hours" indicates the moderator.
Quiz: (True of False) The parameter pairwise ~ gender, var="hours" tells the emtrends that we want pairwise differences in the predicted values of Hours for females versus males.
Answer: False, this is the pairwise difference in the slope of Hours for females versus males. Recall that emtrends obtains simple slopes and emmeans obtains predicted values.
Exercise
Relevel gender so that male is now the reference group, refit the lm model, store again it as a contcont object and use emtrends to obtain the simple slopes.
a) Spell out the new regression equation using a dummy code for gender.
b) Interpret each of coefficients in the new model.
c) What is the main difference in the output compared to using $D_{male}$? What does the naming convention in summary(contcont) represent?
Answers: a) $\hat{\mbox{WeightLoss}}= b_0 + b_1 \mbox{Hours} + b_2 D_{female}+ b_3 \mbox{Hours}*D_{female}$, b) $b_0= 6.906$ is the intercept for males, $b_1 = 1.59$ is the Hours slope for males, $b_2=-3.57$ is the difference in weight loss between female versus males at Hours=0, and $b_3=1.72$ is the additional slope for females, which makes $b_1+b_3=3.31$ the female Hours slope. c) lm and emtrends continue to oppose signs, but both corresponding signs are reversed compared to using females as the reference group. The naming convention genderfemale means that we are using $D_{female}$ and males now belong to the omitted or reference group.
(Optional) Flipping the moderator (MV) and the independent variable (IV)
An interaction is symmetric, which means we can also flip the moderator (gender) so that gender is now the categorical IV and Hours is now the MV. This will reveal to us why $b_2$ is the effect of Gender at Hours = 0. The interaction model is exactly the same, but we decompose the interaction differently.
To see how Gender (IV) varies by levels of Hours (MV), we create a new list with three values of Hours: 0, 2, and 4 hours=c(0,2,4) and gender=c("male","female"). Be aware that the order of the factor variables in the list matters. In our case, gender=c("male","female") tells the function that we want to take male – female.
(mylist <- list(hours=c(0,2,4),gender=c("male","female")))
The simple effect is the difference of two predicted values. Since we are looking at simple effects (not slopes) we cannot use emtrends but rather emmeans. After passing in the object contcat into the emmeans, we request that predicted values of every combination of Hours and Gender be specified in at=mylist and store the output into an object called emcontcat.
emcontcat <- emmeans(contcat, ~ hours*gender, at=mylist)
Pass this new object into a function called contrast where we can request "pairwise" differences (or simple effects) of every effect in our model (in this case gender), moderated by="hours".
Quiz: (True or False) Suppose we use $D_{male}$. If we specified gender=c("female","male")in mylist and then requested "revpairwise" in contrast, we would get the male – female difference. This is consistent with the coefficient of $D_{male}$.
Answer: True, gender=c("female","male") would take female – male, but "revpairwise" reverses this difference to become male – female, which is consistent with the coefficient for $D_{male}.$
> contrast(emcontcat, "pairwise",by="hours")
hours = 0:
contrast estimate SE df t.ratio p.value
male - female 3.571 3.915 896 0.912 0.3619
hours = 2:
contrast estimate SE df t.ratio p.value
male - female 0.123 0.938 896 0.131 0.8955
hours = 4:
contrast estimate SE df t.ratio p.value
male - female -3.325 3.905 896 -0.851 0.3948
We can verify from the output that for hours = 0, the effect 3.571 matches the $b_2$ coefficient, gendermale, confirming that the interpretation of this coefficient is the gender effect at Hours = 0. From our other simple effects we can see that as Hours increases, the male versus female difference becomes more negative (females are losing more weight than males). Take the quiz below to make sure you understand why we don’t see a significant interaction.
Quiz: If the difference of the simple effects for gender (males versus females) is growing more negative as Hours increases, why isn’t our overall interaction significant? (Hint: look at the p-values and standard errors of each simple effect).
Plotting the continuous by categorical interaction
To see why the interaction is not significant, let’s visualize it with a plot. Thankfully, this is easy to accomplish using emmip. Again we want the x-axis to indicate ranges of Hours between 0 and 4 by increments of 0.4 just as in the continuous by continuous example. The only difference is we swap the moderator from effort to gender with two levels, female and male. The order matters for the legend, here female is on top. Pass the lm object contcat into this function, use gender ~hours to indicate that Hours is on the x-axis and Gender is the moderator that separates lines. We specify which values to plot the figure using at=mylist (which we previously specified), and finally we request confidence intervals using CIs=TRUE.
(mylist <- list(hours=seq(0,4,by=0.4),gender=c("female","male")))
emmip(contcat, gender ~hours, at=mylist,CIs=TRUE)
The resulting figure is shown below:
Although it looks like there’s a cross-over interaction, the large overlap in confidence intervals suggests that the slope of Hours is not different between males and females. We confirm that the standard error of the interaction coefficient (1.898) is large relative to the absolute value of the coefficient itself (1.724).
Quiz: (True or False) Looking at the plot, since Hours is on the x-axis it is the IV and Gender separates the lines so it is the moderator (MV).
Answer: True.
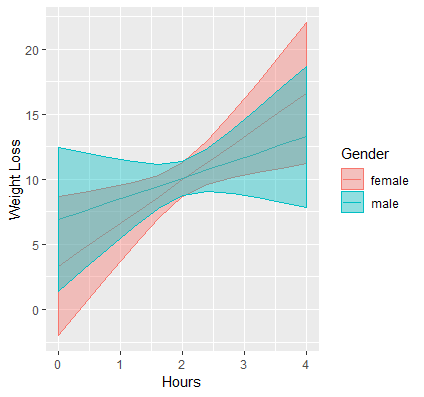
(Optional) Exercise
Plot the same interaction using ggplot by following the instructions for the continuous by continuous interaction. The resulting plot should look like the figure below. Notice the large overlap of the confidence intervals between males and females.
Categorical by Categorical
Now that we understand how one categorical variable interacts with an IV, let’s explore how the interaction of two categorical variables is modeled. From our previous analysis, we found that there are no gender differences in the relationship of time spent exercising and weight loss. Perhaps females and males respond differently to different types of exercise (here we make gender the IV and exercise type the MV). The question we ask is, does type of exercise (W) moderate the gender effect (X)? In other words, do males and females lose weight differently depending on the type of exercise they engage in? Just as before, we must dummy code gender into $D_{male}$ and $D_{female}$, and we choose to omit $D_{female}$, making females the reference group. The difference between this model and the previous model is that we have two categorical variables, where the IV is gender and the MV is now exercise type: jogging, swimming and control group “reading”.
In order to create the dummy codes for exercise type (labeled prog in the data), recall that we have as many dummy codes as there are categories, but we retain only $k-1$ of them. In this case, we have $D_{jog} = 1$ if jogging, $D_{swim} = 1$ if swimming, and $D_{read} = 1$ if reading. It makes sense to make our control group the reference group, so we choose to omit $D_{read}.$ Therefore we retain $D_{male}$ for males, and $D_{jog}$ and $D_{swim}$ which correspond to jogging and swimming.
To see why the dummy code for reading is redundant, suppose we know that for a particular person $D_{jog}=0$, $D_{swim}=0$. Since this person is not in the jogging or swimming condition, we can conclude that this person is in the reading condition. Therefore, knowing $D_{read}=1$ provides no additional information from knowing only $D_{jog}=0$ and $D_{swim}=0$. Here is the exhaustive list of all membership categories using just jogging and swimming dummy codes:
- $D_{jog}=1,D_{swim}=0$: the participant is in the jogging condition.
- $D_{jog}=0,D_{swim}=1$: the participant is in the swimming condition.
- $D_{jog}=0,D_{swim}=0$: the participant is not in jogging and not in swimming, therefore she must be in reading.
- $D_{jog}=1,D_{swim}=1$: participant is in both jogging and swimming, we assume this is impossible, since the participant must be exclusively in one of the groups.
We are now ready to set up the interaction of two categorical variables. Since the interaction of two IV’s is their product, we would multiply the included dummy codes for Males by the included dummy codes for Exercise. Since $D_{male}$ is included for Gender and $D_{jog}$ and $D_{swim}$ are included for Exercise, their products are $D_{male} *D_{jog}$ and $D_{male} *D_{swim}$. Including the product terms and the lower order terms in our model we have:
$$\hat{\mbox{WeightLoss}}= b_0 + b_1 D_{male} + b_2 D_{jog} + b_3 D_{swim} + b_4 D_{male}*D_{jog} + b_5 D_{male}*D_{swim}$$
Before fitting this model in R, we have to make sure we tell R which category to make the reference (or omitted group).
dat$prog <- relevel(dat$prog, ref="read") dat$gender <- relevel(dat$gender, ref="female")
R does not distinguish between a binary and categorical variable with more than two categories. No matter how many categories $k$, R will fit $k-1$ dummy codes into your regression model treating the reference category you define as the omitted category. Therefore, re-leveling Gender and re-leveling Exercise just requires one step.
Now that we’ve redefined our reference group, we are ready to fit the categorical by categorical interaction model in R with the following code:
catcat <- lm(loss~gender*prog,data=dat) summary(catcat)
We then obtain the following shortened output:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.6201 0.5322 -6.802 1.89e-11 ***
gendermale -0.3355 0.7527 -0.446 0.656
progjog 7.9088 0.7527 10.507 < 2e-16 ***
progswim 32.7378 0.7527 43.494 < 2e-16 ***
gendermale:progjog 7.8188 1.0645 7.345 4.63e-13 ***
gendermale:progswim -6.2599 1.0645 -5.881 5.77e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
There are two interaction terms, one for male by jogging and the other for male by swimming, and both of them are significant. Let’s interpret each of the terms in the model:.
- $b_0$
(Intercept): the intercept, or the predicted weight loss when $D_{male} = 0$ and $D_{jog}=0, D_{swim}=0$ (i.e., the intercept for females in the reading program) - $b_1$
gendermale: the simple effect of males for $D_{jog}=0, D_{swim}=0$ (i.e., the male – female weight loss in the reading group). - $b_2$
progjog: the simple effect of jogging when $D_{male} = 0$ (i.e., the difference in weight loss between jogging versus reading for females). - $b_3$
progswim: the simple effect of swimming when $D_{male} = 0$ (i.e., the difference in weight loss between swimming versus reading for females). - $b_4$
gendermale:progjog: the interaction of $D_{male}$ and $D_{jog}$, the male effect (male – female) in the jogging condition versus the male effect in the reading condition. Also, the jogging effect (jogging – reading) for males versus the jogging effect for females. - $b_5$
gendermale:progswim: the interaction of $D_{male}$ and $D_{swim}$, the male effect (male – female) in the swimming condition versus the male effect in the reading condition. Also, the swimming effect (swimming- reading) for males versus the swimming effect for females.
The last two coefficients are the most difficult to interpret. We can think of $b_4$ as the additional male effect of going from reading to jogging and $b_5$ as the additional male effect going from reading to swimming:
- $b_1+b_4$
gendermale+gendermale:progjogis the simple effect of males in the jogging group, - $b_1+b_5$
gendermale+gendermale:progswimis the simple effect of males in the swimming group.
We can confirm this is true for jogging if we subtract the interaction term $b_4$, the additional male effect for jogging, from $(b_1+b_4)$. Then $(b_1+b_4) – b_4 = b_1$ which from above we know is the male effect in the reading group.
Quiz: Use the coefficients from the categorical by categorical interaction to derive the female (female – male) effect for the swimming group. (Hint: flip the sign of the coefficient)
Answer: $-b_1+(-b_5)=-(b_1+b_5)=-(-0.336+(-6.26))=6.60.$
Simple effects in a categorical by categorical interaction
Although the coefficients in the categorical by categorical regression model are a bit difficult to interpret, it is surprisingly easy to obtain predicted values from a software package like emmeans. First let’s define the emmeans syntax and store it in an object called emcatcat.
emcatcat <- emmeans(catcat, ~ gender*prog)
Since gender and prog are both factors, emmeans automatically knows to calculate the predicted values. The ~ gender*prog tells the function that we want the predicted values broken down by all possible combinations of the two categorical (factor) variables.
gender prog emmean SE df lower.CL upper.CL female read -3.62 0.532 894 -4.66 -2.58 male read -3.96 0.532 894 -5.00 -2.91 female jog 4.29 0.532 894 3.24 5.33 male jog 11.77 0.532 894 10.73 12.82 female swim 29.12 0.532 894 28.07 30.16 male swim 22.52 0.532 894 21.48 23.57 Confidence level used: 0.95
These are the predicted values of weight loss for all combinations of Gender and Exercise. For example, females in the reading program have an estimated weight gain of 3.62 pounds, whereas males in the swimming program have an average weight loss of 22.52 pounds (how nice if this were true!).
Exercise
Try to reproduce each predicted value from emcatcat using the summary table alone. Do you notice a pattern for the coefficient terms?
Answer: In order of the table: \begin{eqnarray} (b_0) & & &=& -3.62 \\ (b_0 + b_1) &=& -3.62 + (-0.336) &=&-3.96 \\ (b_0) + b_2 &=& -3.62 + 7.91&=&4.29 \\ (b_0 + b_1) + b_2 + b_4 &=& -3.62 + (-0.336) + 7.91 + 7.82&=&11.77 \\ (b_0)+b_3 &=& -3.62 + 32.74&=&29.12 \\ (b_0+b_1)+b_3+b_5 &=& -3.62 + (-0.336)+32.74+(-6.25)&=& 22.53 \end{eqnarray}
There are many possible patterns, but one pattern is to start with $(b_0)$ for females, $(b_0+b_1)$ for males, then add on additional terms. For females, the additional terms do not involve interaction terms, but for males it does. For example, for females in the jogging group, start with $b_0$ which is predicted weight loss for females in the reading group, then add on the additional effect of jogging for females which is $b_2$. For males in the jogging group, first obtain the predicted value of males in the reading group $(b_0+b_1)$, then add $(b_2 + b_4)$ which is the additional jogging effect for males ($b_4$ is the jogging versus reading effect above the jogging versus reading effect for females).
In order to understand the interaction, we need to obtain the simple effects which are differences of the predicted values. This can be accomplished using the contrast function as part of emmeans. Since we previously stored our emmeans object in emcatcat, we can call it back and pass it as a parameter into the contrast function.
> contrast(emcatcat, "revpairwise",by="prog",adjust="none") prog = read: contrast estimate SE df t.ratio p.value male - female -0.335 0.753 894 -0.446 0.6559 prog = jog: contrast estimate SE df t.ratio p.value male - female 7.483 0.753 894 9.942 <.0001 prog = swim: contrast estimate SE df t.ratio p.value male - female -6.595 0.753 894 -8.762 <.0001
Pass in object emcatcat into contrast and request "revpairwise" differences (simple effects) split by="prog". We use "revpairwise" rather than "pairwise" because by default the reference group (female) would come first. Finally we request no adjustment to the p-value. In practice however, it may be advisable to correct for multiple comparisons to guard against Type I error (the probability of making a false rejection of the null hypothesis), or false positives. If you do not specify anything, Tukey is the default, and the end of the output would show the following which varies depending on the number of estimates in your model:
P value adjustment: tukey method for comparing a family of 3 estimates
Going back to the output from the contrast statement, we see that the male effect for jogging and swimming are significant at the 0.05 level (with no adjustment of p-values), but not for the reading condition. Additionally, males lose more weight in the jogging condition (positive) but females lose more weight in the swimming condition (negative).
Quiz: (True or False) The interaction is the male effect for a particular exercise type.
Answer: False. See below.
The male effect alone does not capture the interaction. The interaction is the difference of simple effects. Going back to the output from summary(catcat), let’s see if we can recreate $b_5=-6.26$ which is the interaction of male by swimming using the output from contrast.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
gendermale:progswim -6.2599 1.0645 -5.881 5.77e-09 ***
Recall that the interaction is the difference of simple effects. In this case, we want the difference in the male effect (males vs. females) in the swimming condition and the male effect in the reading condition. From contrast, recall that the gender effect for swimming is -6.59 and the gender effect for reading is -0.335. Then the difference of the two simple effects is -6.595-(-0.335) = -6.26, which matches our output from the original regression. We verify therefore that the interaction is the pairwise difference of the male effects (male-female) for swimming versus reading. It is essentially a difference of differences.
Exercise
Find the interaction that is not automatically generated by the original regression output and obtain its effect by manually calculating the difference of differences using the output from contrast. Confirm your answer with a regression (Hint: you need to change the reference group).
Optional Exercise: We have been focusing mostly on the gender effect (IV) split by exercise type (MV). However, an interaction is symmetric which means we can also look at the effect of exercise type (IV) split by gender (MV). Obtain the same interaction term using contrast with gender as the moderator.
Answer: $7.48-(-6.595) = 14.08$, the interaction of jogging versus swim by gender. Running summary(catcat) should produce the following shortened code:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
gendermale:progjog 14.0787 1.0645 13.226 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Answer to Optional Exercise: contrast(emcatcat,"revpairwise",by="gender",adjust="none"), $-10.75-(-24.83) = 14.08.$ This is the difference in the jogging effect for males versus females (difference of differences), treating Gender as the MV. In the previous example, we treated Exercise as the MV so that the interpretation is the difference in the gender effect for jogging vs. reading.
Plotting the categorical by categorical interaction
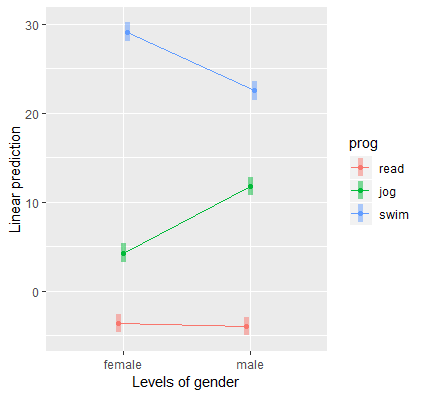
Finally, the best way to understand an interaction is to plot it. The emmip function takes in our original lm object catcat and prog ~ gender tells emmip that we want to plot gender along the x-axis and split the lines by exercise type. Finally, we request confidence bands using CIs=TRUE.
emmip(catcat, prog ~ gender,CIs=TRUE)
Quiz: (True or False) The plotting function emmip requires predicted values from emmeans as input in a categorical by categorical interaction.
Answer: False, it requires input from the lm object or the linear regression itself, not the predicted values.
We obtain the following interaction plot:
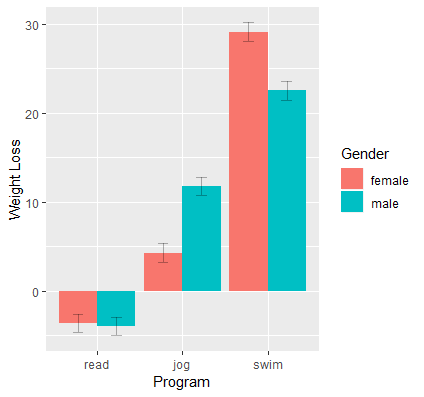
Here we see the results confirming the predicted values and simple effects we found before. Each point on the plot is a predicted value and each line or connection of two points is a simple effect. Exercise type (prog) is the moderator of the gender effect (gender), and we see a negative effect for swimming (females lose more weight swimming) and a positive effect for jogging (men lose more weight jogging). Females and males lose about the same amount of weight for the reading condition. Since we have simple effects rather than simple slopes, some researchers prefer bar graphs for representing categorical changes in effects.
Quiz: How would we plot exercise type along the x-axis split by gender? Which plot makes more sense to you?
Answer: emmip(catcat, gender ~ prog, CIs=TRUE). The independent variable (IV) should always be the focus of the study, and the moderator (MV) is the variable that changes the primary relationship of the IV on the DV. If exercise type is on the x-axis then the researcher is primarily interested in how exercise type influences weight loss but is also interested in whether males and females respond differently to various exercise modalities.
(Optional) Plotting simple effects using bar graphs with ggplot
Some researchers prefer to depict simple effects using bar graphs rather than line graphs. Recall that we use can emmip and specify plotit=FALSE so that we can output the predicted values into a new data frame catcatdat.
catcatdat <- emmip(catcat, gender ~ prog, CIs=TRUE, plotit=FALSE)
The output is familiar to us from the continuous by continuous interaction. The only difference is that instead of numeric values we have factors for gender and exercise type.
gender prog yvar SE df LCL UCL tvar xvar 1 female read -3.620149 0.5322428 894 -4.664740 -2.575559 female read 2 male read -3.955606 0.5322428 894 -5.000197 -2.911016 male read 3 female jog 4.288681 0.5322428 894 3.244091 5.333272 female jog 4 male jog 11.772028 0.5322428 894 10.727437 12.816619 male jog 5 female swim 29.117691 0.5322428 894 28.073100 30.162282 female swim 6 male swim 22.522383 0.5322428 894 21.477792 23.566974 male swim
Since gender and prog are already factors in the original data frame, we do not need to specify the factor variables again in our new data frame. Now we are ready to use ggplot. First, pass the data frame catcatdat. Since we want gender to fill in the entire bar rather than outline its shape, map gender into the fill aesthetic rather than color. Within aes(), we want exercise type to be on the x-axis using x=prog and our predicted value to be on the y-axis using y=yvar. Then, add a bar graph using geom_bar(). By default, the bar graph will simply populate a count of the number of participants in each exercise type. Instead we want the y-axis to be the predicted values, so we specify this by using stat="identity". Additionally, by default, the bar graphs are stacked, which is good for counts of the sample size, but not meaningful for our predicted values, so we position female and male graphs side by side using position="dodge".
p <- ggplot(data=catcatdat, aes(x=prog,y=yvar, fill=gender)) + geom_bar(stat="identity",position="dodge")
The results of the graph is shown below:
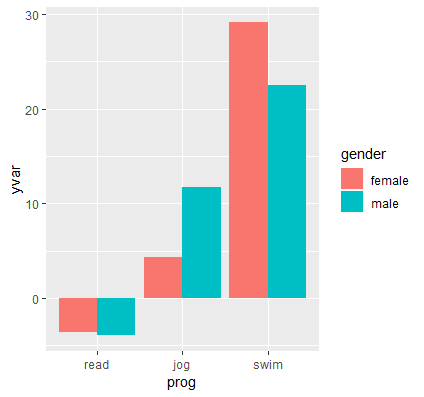
The next series of steps adds error bars using geom_errorbar. First, pass in the upper and lower limits of the error bars using ymax=UCL, ymin=LCL. Now focus on the size and location of the error bars. By default, the error bar positions lie in the middle of both bar graphs, so we specify the position as 0.9 using position=position_dodge(.9). The value here is hard to understand, the best way is to try different values until you get the desired position. Additionally, the error bars span the entire width of both bar graphs, so specify width=.25 to shorten its width. Finally, we add a bit of transparency to the error bars so it doesn’t take precedent over the whole bar graph using alpha=0.3. Recall that alpha values closer to zero result in more transparent error bars.
p1 <- p + geom_errorbar(position=position_dodge(.9),width=.25, aes(ymax=UCL, ymin=LCL),alpha=0.3)
The last steps involve changing our labels so the x-axis is labeled “Program”, the y-axis is “Weight Loss” (you can also label it “Predicted Weight Loss” so that we know these come from the linear model), and the legend is “Gender”.
p1 + labs(x="Program", y="Weight Loss", fill="Gender")
Now we have a publication quality figure which is fitting for categorical variables.
Conclusion
As a researcher, the question you ask should determine which interaction model you choose. Hopefully we have exhausted all the types of research questions you can ask with the interaction of two variables. Recall that coefficients for IV’s interacted with an MV are interpreted as simple effects (or slopes) fixed at 0 of the MV, whereas coefficients for IV’s not interacted with others are main effects (or slopes) meaning that its effect does not vary by the level of another IV. The interaction itself always involves differences of simple effects or slopes. Researchers who are just starting out with interaction hypotheses often confuse testing the simple slope (or effects) against zero versus the interaction, which tests whether the difference of simple slopes (or effects) are different from zero. Another common point of confusion is the idea of a predicted value versus a simple slope slope (or effect). A predicted value is a single point on the graph, whereas a simple slope (or effect) is a difference of two predicted values. Furthermore, an interaction is a difference of two simple slopes (or effects). To summarize these concepts geometrically:
- Predicted values are points on the graph.
- Simple effects or slopes are the difference between two predicted values (i.e., two points).
- Interactions are the difference between simple effects of slopes;
- for an interaction involving a continuous IV, it’s the difference of two slopes (i.e., two lines)
- for a categorical by categorical interaction, the interaction is the difference in the height of the bars in one group versus the difference of the heights in another group (a.k.a., difference of differences).
It may be instructive to plot the regression and rephrase your research question using the geometric representations of the graph.
Final Exercise
Return to a plot in each type of interaction and identify four predicted values, two corresponding simple slopes or effects and the corresponding interaction.
Thank you taking the time to read this seminar. We hope the material will help you in your research endeavors.