This is a draft version of this chapter. Comments and suggestions to improve this draft are welcome.
Chapter outline
6.1. Analysis with two categorical variables
6.2. Simple effects
6.2.1 Analyzing simple effects using xi3 and regress
6.2.2 Coding of simple effects
6.3. Simple comparisons
6.3.1 Analyzing simple comparisons using xi3 and regress
6.3.2 Coding of simple comparisons
6.4. Partial interaction
6.4.1 Analyzing partial interactions using xi3 and regress
6.4.2 Coding of partial interactions
6.5. Interaction contrasts
6.5.1 Analyzing interaction contrasts using xi3 and regress
6.5.2 Coding of interaction contrasts
6.6. Computing adjusted means
6.6.1 Computing adjusted means via anova
6.6.1 Computing adjusted means via regress
6.7. More details on meaning of coefficients
6.8. Simple effects via dummy coding versus effect coding
6.8.1 Example 1. Simple effects of yr_rnd at levels of mealcat
6.8.2 Example 2. Simple effects of mealcat at levels of yr_rnd
Please note: This page makes use of the programs xi3 and postgr3 which are no longer being maintained and has been removed from our archives. References to xi3 and postgr3 will be left on this page because they illustrate specific principles of coding categorical variables.
For this chapter we will use the elemapi2 data file that we have been using in prior chapters. We will focus on the variables mealcat, and collcat as they relate to the outcome variable api00 (performance on the api in the year 2000). The variable mealcat is the variable meals broken up into three categories, and the variable collcat is the variable some_col broken into 3 categories. We could think of mealcat as being the number of students receiving free meals and broken up into low, middle and high. The variable collcat can be thought of as the number of parents with some college education, and we could think of it as being broken up into low, medium and high. For our analysis, we think that both mealcat and collcat may be related to api00, but it is also possible that the impact of mealcat might depend on the level of collcat. In other words, we think that there might be an interaction of these two categorical variables. In this chapter we will look at how these two categorical variables are related to api performance in the school, and we will look at the interaction of these two categorical variables as well. We will see that there is an interaction of these categorical variables, and will focus on different ways of further exploring the interaction.
We will first use the elemapi2 data file.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
We will modify the label for mealcat in order to more clearly see some of the points we will be demonstrating later in this chapter.
label define mealcat 1 "1" 2 "2" 3 "3", modify
6.1. Analysis with 2 categorical variables
One traditional way to analyze this would be to perform a 3 by 3 factorial analysis of variance using the anova command, as shown below. The results show a main effect of collcat (F=4.5, p-0.0117), a main effect of mealcat (F=509.04, p=0.0000) and an interaction of collcat by mealcat, (F=6.63, p=0.0000).
anova api00 collcat mealcat collcat*mealcat
Number of obs = 400 R-squared = 0.7733
Root MSE = 68.412 Adj R-squared = 0.7687
Source | Partial SS df MS F Prob > F
----------------+----------------------------------------------------
Model | 6243714.81 8 780464.351 166.76 0.0000
|
collcat | 42140.5662 2 21070.2831 4.50 0.0117
mealcat | 4764843.56 2 2382421.78 509.04 0.0000
collcat*mealcat | 124167.809 4 31041.9522 6.63 0.0000
|
Residual | 1829957.19 391 4680.19741
----------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
We can use the adjust command to show the adjusted means broken down by collcat and mealcat.
adjust, by(collcat mealcat)
----------------------------------------------------------
Dependent variable: api00 Command: anova
----------------------------------------------------------
-------------------------------------
|Percentage free meals in 3
| categories
collcat | 1 2 3
----------+--------------------------
1 | 816.914 589.35 493.919
2 | 825.651 636.605 508.833
3 | 782.151 655.638 541.733
-------------------------------------
Key: Linear Prediction
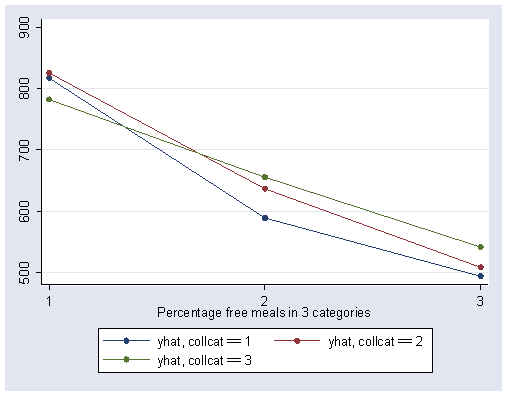
We can show a graph of the adjusted means as shown below. We use the separate command to make three variables corresponding to the three levels of collcat (i.e., yhat1 corresponds to the predicted value when collcat is low). We can then show the graph with the three levels of collcat represented as three separate lines.
predict yhat separate yhat, by(collcat)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- yhat1 float %9.0g yhat, collcat == 1 yhat2 float %9.0g yhat, collcat == 2 yhat3 float %9.0g yhat, collcat == 3
graph twoway scatter yhat1 yhat2 yhat3 mealcat, connect(l l l) xlabel(1 2 3) sort
Now we drop the variables yhat yhat1 yhat2 yhat3 in case we wish to use these variables later.
drop yhat yhat1 yhat2 yhat3
We can do these same analyses using the regress command. Below we use the regress command with xi3 to look at the effect of collcat, mealcat and the interaction of these two variables.
xi3: regress api00 g.collcat*g.mealcat
. xi3: regress api00 g.collcat*g.mealcat
g.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted)
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icollcat_2 | 23.63531 9.105331 2.60 0.010 5.733782 41.53685
_Icollcat_3 | 26.44625 9.995129 2.65 0.008 6.795331 46.09717
_Imealcat_2 | -181.0414 9.077126 -19.94 0.000 -198.8874 -163.1953
_Imealcat_3 | -293.4103 9.449459 -31.05 0.000 -311.9884 -274.8322
_Ico2Xme2 | 38.51777 24.19532 1.59 0.112 -9.051422 86.08697
_Ico2Xme3 | 6.177537 20.08262 0.31 0.759 -33.3059 45.66097
_Ico3Xme2 | 101.051 22.88808 4.42 0.000 56.05191 146.0501
_Ico3Xme3 | 82.57776 24.43941 3.38 0.001 34.52867 130.6268
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
We use the test command to test the two terms associated with collcat to get the main effect of collcat.
test _Icollcat_2 _Icollcat_3
( 1) _Icollcat_2 = 0.0
( 2) _Icollcat_3 = 0.0
F( 2, 391) = 4.50
Prob > F = 0.0117
Likewise we use the test command to get the overall test of mealcat.
test _Imealcat_2 _Imealcat_3
( 1) _Imealcat_2 = 0.0
( 2) _Imealcat_3 = 0.0
F( 2, 391) = 509.04
Prob > F = 0.0000
Finally, we use the test command to test the interaction of of collcat by mealcat.
test _Ico2Xme2 _Ico2Xme3 _Ico3Xme2 _Ico3Xme3
( 1) _Ico2Xme2 = 0
( 2) _Ico2Xme3 = 0
( 3) _Ico3Xme2 = 0
( 4) _Ico3Xme3 = 0
F( 4, 391) = 6.63
Prob > F = 0.0000
First, note that the results of the test commands correspond to those from the anova command above. This is because collcat and mealcat were coded using simple effect coding, a coding scheme where the contrasts sum to 0. We indicated that we wanted simple effect coding by using g.collcat and g.mealcat on the regress command with xi3 (see Chapter 5 for more information about coding schemes available via the xi3 command). If this had been coded using dummy coding, e.g., i.collcat, then the results of the test commands for mealcat and somecat from the regress command would not have corresponded to the anova results. In addition to simple effect coding, we could have used e., h., r., a., b., or o. and the results of the test commands would have matched the anova command, although the meaning of the individual tests would have been different. This point will be explored in more detail later in this chapter.
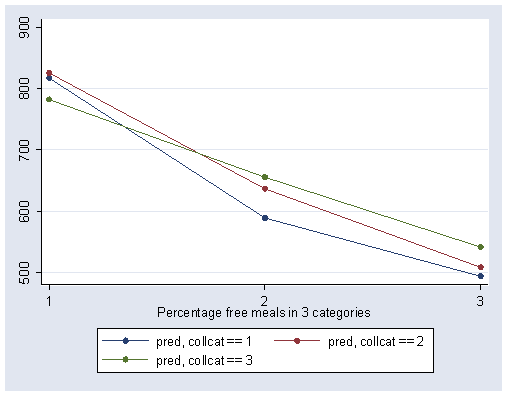
We can obtain the adjusted means by using predict command to get the predicted values, calling them pred and then looking at the mean of pred broken down by collcat and mealcat.
predict pred table collcat mealcat, contents(mean pred)
Means, Standard Deviations and Frequencies of Fitted values
| Percentage free meals in 3
| categories
collcat | 1 2 3 | Total
-----------+---------------------------------+----------
1 | 816.91431 589.34998 493.91891 | 596.34884
2 | 825.65118 636.60468 508.83334 | 651.50002
3 | 782.15094 655.6377 541.73334 | 692.1095
-----------+---------------------------------+----------
Total | 805.71757 639.39395 504.37956 | 647.62251
We can show a graph of cell means as shown below. We use the same strategy as we did in making the graph above.
separate pred, by(collcat)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- pred1 float %9.0g pred, collcat == 1 pred2 float %9.0g pred, collcat == 2 pred3 float %9.0g pred, collcat == 3
graph twoway scatter pred1 pred2 pred3 mealcat, c(l l l) xlabel(1 2 3) sort
Now we drop the variables pred pred1 pred2 pred3 in case we wish to use these variable names later.
drop pred pred1 pred2 pred3
Note that we could have produced the same graph and table of predicted values using the postgr3 command.
postgr3 mealcat, by(collcat) table2 clpattern(solid dash dot)
Variables left asis: _Imealcat_2 _Imealcat_3 _Icollcat_2 _Icollcat_3 _IcolXmea_2_2 _IcolXmea_2_3 _IcolXmea_3_2 _IcolXmea_3_3 (option xb assumed; fitted values)
Means of Fitted values
| Percentage free meals in 3
| categories
collcat | 1 2 3 | Total
-----------+---------------------------------+----------
1 | 816.91431 589.34998 493.91891 | 596.34884
2 | 825.65118 636.60468 508.83334 | 651.50002
3 | 782.15094 655.6377 541.73334 | 692.1095
-----------+---------------------------------+----------
Total | 805.71757 639.39395 504.37956 | 647.62251
The graph of the cell means illustrates the interaction between collcat and mealcat. The graph shows the three levels of collcat as three different lines, and the three levels of mealcat as the three values on the x-axis of the graph. We can see that the effect of collcat differs based on the level of mealcat. For example, when mealcat is low, schools where collcat is 3 have the lowest api00 scores, as compared to schools that are medium or high on mealcat, where schools with collcat of 3 have the highest api00 scores.
Let’s investigate this interaction further by looking at the simple effects of collcat at each level of mealcat.
6.2. Simple effects
We found that the main effect of collcat was significant, but because we have an interaction the effect of collcat depends on the level of mealcat. We might want to ask whether the effect of collcat is significant at each level of mealcat.
6.2.1 Analyzing simple effects using xi3 and regress
In order to look at the simple effects of collcat at the different levels of mealcat, we will use the @ symbol instead of * to indicate that we want the interaction terms to reflect the simple effects of collcat at each level of mealcat. We will use helmert coding for collcat, which will be discussed further later.
xi3: regress api00 h.collcat@g.mealcat
h.collcat _Icollcat_1-3 (naturally coded; _Icollcat_3 omitted)
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_2 | -181.0414 9.077126 -19.94 0.000 -198.8874 -163.1953
_Imealcat_3 | -293.4103 9.449459 -31.05 0.000 -311.9884 -274.8322
_Ico1Wme1 | 13.01323 13.528 0.96 0.337 -13.58349 39.60995
_Ico1Wme2 | -56.77117 16.67866 -3.40 0.001 -89.56223 -23.9801
_Ico1Wme3 | -31.36441 12.86955 -2.44 0.015 -56.66658 -6.062246
_Ico2Wme1 | 43.50022 14.04092 3.10 0.002 15.89507 71.10536
_Ico2Wme2 | -19.03303 13.29175 -1.43 0.153 -45.16528 7.09922
_Ico2Wme3 | -32.9 20.23653 -1.63 0.105 -72.68603 6.886029
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
We can obtain the simple effect of collcat when mealcat is low (i.e., 1) via the test command below. This shows that the effect of collcat when mealcat is low is significant.
test _Ico1Wme1 _Ico2Wme1
( 1) _Ico1Wme1 = 0.0
( 2) _Ico2Wme1 = 0.0
F( 2, 391) = 5.44
Prob > F = 0.0047
We use the describe command below to see the meaning of these terms and see that these two terms represent the two comparisons on collcat when mealcat is 1. For example, in the term _Ico2Wme1, the 2 means that this is the second comparison on collcat and the 1 means that it is when mealcat is 1.
describe _Ico1Wme1 _Ico2Wme1
storage display value variable name type format label variable label ------------------------------------------------------------------------------- _Ico1Wme1 double %10.0g collcat(1 vs. 2+) @ mealcat==1 _Ico2Wme1 double %10.0g collcat(2 vs. 3) @ mealcat==1
We can test the simple effect of collcat when mealcat is 2 via the test command below. This shows that collcat is significant when mealcat is 2.
test _Ico1Wme2 _Ico2Wme2
( 1) _Ico1Wme2 = 0.0
( 2) _Ico1Wme2 = 0.0
F( 2, 391) = 7.33
Prob > F = 0.0007
We can also test the simple effect of collcat when mealcat is 3 via the test command below. This shows that collcat is significant when mealcat is 3, if we use an alpha level of 0.05. We should note that since we are doing a number of additional tests, you might want to consider using post hoc corrections, such as a bonferoni correction to avoid Type I errors.
test _Ico1Wme3 _Ico2Wme3
( 1) _Ico1Wme3 = 0.0
( 2) _Ico2Wme3 = 0.0
F( 2, 391) = 3.20
Prob > F = 0.0417
In summary, all three of the simple effects of collcat at each level of mealcat were significant. However, the effect of collcat when mealcat was 3 might not be significant if we used a post hoc criteria for evaluating its significance.
6.2.2 Coding of simple effects
While xi3 creates the coding for you, it is useful to see the coding it creates for making these simple effects. The coding for mealcat used simple coding, and it’s coding is just as we saw in chapter 5. Below we use the tablist command to show the coding for mealcat. You can download tablist from within Stata by typing search tablist (see How can I used the search command to search for programs and get additional help? for more information about using search).
We see that the coding of mealcat is just as we would expect from chapter 5.
tablist mealcat _Imealcat_2 _Imealcat_3, sort(v)
mealcat _Imealca~2 _Imealca~3 Freq
1 -.33333333 -.33333333 131
2 .66666667 -.33333333 132
3 -.33333333 .66666667 137
We requested helmert coding for collcat, and we can look at the coding of collcat to see that the terms _Icollcat_1 _Icollcat_2 are indeed coded using helmert coding. We should note that these terms are not used in the analysis, but are used by xi3 for creating the simple effects shown in the next section.
tablist collcat _Icollcat_1 _Icollcat_2, sort(v)
collcat _Icollca~1 _Icollca~2 Freq
1 .66666667 0 129
2 -.33333333 .5 134
3 -.33333333 -.5 137
Now that we have seen the helmert coding for collcat, we can see how this is used to create the simple effects of collcat at each level of mealcat. First, we look at the two comparisons of collcat at mealcat of 1. Note that the coding is the same as we saw above, but only when mealcat is 1, otherwise these variables are coded 0.
tablist mealcat collcat _Ico1Wme1 _Ico2Wme1, sort(v)
mealcat collcat _Ico1Wme1 _Ico2W~1 Freq
1 1 .66666667 0 35
1 2 -.33333333 .5 43
1 3 -.33333333 -.5 53
2 1 0 0 20
2 2 0 0 43
2 3 0 0 69
3 1 0 0 74
3 2 0 0 48
3 3 0 0 15
Likewise, we look at the terms that form the effects of collcat when mealcat is 2, and we see that the variables are coded the same way when mealcat is 2, and otherwise 0.
tablist mealcat collcat _Ico1Wme2 _Ico2Wme2, sort(v)
mealcat collcat _Ico1Wme2 _Ico2W~2 Freq
1 1 0 0 35
1 2 0 0 43
1 3 0 0 53
2 1 .66666667 0 20
2 2 -.33333333 .5 43
2 3 -.33333333 -.5 69
3 1 0 0 74
3 2 0 0 48
3 3 0 0 15
Finally, we see the same pattern for the terms that form the effect of collcat when mealcat is 3.
tablist mealcat collcat _Ico1Wme3 _Ico2Wme3, sort(v)
mealcat collcat _Ico1Wme3 _Ico2W~3 Freq
1 1 0 0 35
1 2 0 0 43
1 3 0 0 53
2 1 0 0 20
2 2 0 0 43
2 3 0 0 69
3 1 .66666667 0 74
3 2 -.33333333 .5 48
3 3 -.33333333 -.5 15
This illustrates how xi3 codes the variables to allow the simple effects analysis. If you wished, you could manually create variables according to this strategy to perform a simple effects analysis.
3. Simple comparisons
In the analyses above we looked at the simple effect of collcat at each level of mealcat. For example, we looked at the overall effect of collcat when mealcat was 1. This is the simple effect of collcat at mealcat=1. Because collcat has more than two levels, we may wish to make further comparisons among the three levels of collcat within mealcat=1. Simple comparisons allow us to make such comparisons.
6.3.1 Analyzing Simple Comparisons Using xi3 and regress
In the analyses above we used helmert coding for collcat. We chose this coding so we could compare group 1 with groups 2 and 3 and then compare groups 2 and 3. For example, if we wanted to compare collcat 1 versus 2 and 3, we would want to look at the effect _Ico1Wme1, and if we wanted to compare collcat groups 2 and 3 when mealcat is 1, then we would look at the effect _Ico2Wme1. Because xi3 creates labels for each term that it creates, we can use the describe command to verify that we are using the correct terms. Indeed, we see that these terms are as we expected.
describe _Ico1Wme1 _Ico2Wme1
storage display value variable name type format label variable label ------------------------------------------------------------------------------- _Ico1Wme1 double %10.0g collcat(1 vs. 2+) @ mealcat==1 _Ico1Wme1 double %10.0g collcat(2 vs. 3) @ mealcat==1
We can use the regress command to see the effects for these terms.
regress
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_2 | -181.0414 9.077126 -19.94 0.000 -198.8874 -163.1953
_Imealcat_3 | -293.4103 9.449459 -31.05 0.000 -311.9884 -274.8322
_Ico1Wme1 | 13.01323 13.528 0.96 0.337 -13.58349 39.60995
_Ico1Wme2 | -56.77117 16.67866 -3.40 0.001 -89.56223 -23.9801
_Ico1Wme3 | -31.36441 12.86955 -2.44 0.015 -56.66658 -6.062246
_Ico2Wme1 | 43.50022 14.04092 3.10 0.002 15.89507 71.10536
_Ico2Wme2 | -19.03303 13.29175 -1.43 0.153 -45.16528 7.09922
_Ico2Wme3 | -32.9 20.23653 -1.63 0.105 -72.68603 6.886029
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
We see that the collcat 1 is not significantly different from 2 and 3 at mealcat 1 (t=.96, p=.337), but collcat 2 is significantly different from collcat 3 at mealcat 1 (t=3.10, p=0.002).
6.3.2 Coding of Simple Comparisons
We can see that the coding of simple comparisons is the same as the coding of simple effects. For example, we can see that the coding of _Icollcat_1 and _Icollcat_2 is coded using helmert coding.
tablist collcat _Icollcat_1 _Icollcat_2, sort(v)
collcat _Icollca~1 _Icollca~2 Freq
1 .66666667 0 129
2 -.33333333 .5 134
3 -.33333333 -.5 137
Then the term term _Ico1Wme1 represents the comparison of collcat 1 versus collcat 2 and 3 when mealcat is 1. Hence, the coding is the same as the coding for _Icollcat_1 when mealcat is 1, and 0 otherwise, see below.
tablist mealcat collcat _Ico1Wme1, sort(v)
mealcat collcat _Ico1Wme1 Freq
1 1 .66666667 35
1 2 -.33333333 43
1 3 -.33333333 53
2 1 0 20
2 2 0 43
2 3 0 69
3 1 0 74
3 2 0 48
3 3 0 15
6.4. Partial interaction
A partial interaction allows you to apply contrasts to one of the effects in an interaction term. For example, we can draw the interaction of collcat by mealcat like this below.
| Collcat low | Collcat Med | Collcat High | |
| Mealcat Low | |||
| Mealcat Med | |||
| Mealcat High |
Say that we wanted to compare, in the context of this interaction, group 1 for collcat versus groups 2 and 3. The table of this partial interaction would look like this. The contrast coefficients of -2 1 1 applied to collcat indicate the comparison of group 1 for collcat versus groups 2 and 3.
| -2 | 1 | 1 | |
| Collcat low | Collcat Med | Collcat High | |
| Mealcat Low | |||
| Mealcat Med | |||
| Mealcat High |
Likewise, we also might want to compare groups 2 and 3 of collcat by mealcat, and the table of this interaction would look like this.
| 0 | -1 | 1 | |
| Collcat low | Collcat Med | Collcat High | |
| Mealcat Low | |||
| Mealcat Med | |||
| Mealcat High |
These are called partial interactions because contrast coefficients are applied to one of the terms involved in the interaction.
6.4.1 Analyzing partial interactions using xi3 and regress
As shown above, we wish to compare groups 1 versus 2 and 3 on collcat, and then compare groups 2 and 3 on collcat. This implies helmert coding on collcat, as shown below. The coding for mealcat is chosen as forward difference coding (for the purposes of later analyses) but could have been any form of effect coding.
xi3: regress api00 h.collcat*a.mealcat
h.collcat _Icollcat_1-3 (naturally coded; _Icollcat_3 omitted)
a.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icollcat_1 | -25.04078 8.345388 -3.00 0.003 -41.44823 -8.633334
_Icollcat_2 | -2.810937 9.329377 -0.30 0.763 -21.15296 15.53108
_Imealcat_1 | 181.0414 9.077126 19.94 0.000 163.1953 198.8874
_Imealcat_2 | 112.3689 9.907594 11.34 0.000 92.89009 131.8477
_Ico1Xme1 | 69.7844 21.4752 3.25 0.001 27.56308 112.0057
_Ico1Xme2 | -25.40675 21.06663 -1.21 0.229 -66.82479 16.01128
_Ico2Xme1 | 62.53325 19.33438 3.23 0.001 24.5209 100.5456
_Ico2Xme2 | 13.86697 24.21132 0.57 0.567 -33.73369 61.46763
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
Let’s look at all of the terms created by the xi3 command using the describe command.
describe _I*
storage display value variable name type format label variable label ------------------------------------------------------------------------------- _Icollcat_1 double %10.0g collcat(1 vs. 2+) _Icollcat_2 double %10.0g collcat(2 vs. 3) _Imealcat_1 double %10.0g mealcat(1 vs. 2) _Imealcat_2 double %10.0g mealcat(2 vs. 3) _Ico1Xme1 float %9.0g collcat(1 vs. 2+)*mealcat(1 vs. 2) _Ico1Xme2 float %9.0g collcat(1 vs. 2+)*mealcat(2 vs. 3) _Ico2Xme1 float %9.0g collcat(2 vs. 3)*mealcat(1 vs. 2) _Ico2Xme2 float %9.0g collcat(2 vs. 3)*mealcat(2 vs. 3)
The partial interaction of collcat comparing groups 1 versus 2 and 3 by mealcat is composed of the interaction terms _Ico1Xme1 and _Ico1Xme2, because these are the terms from the interaction that compare groups 1 versus 2 and 3 on collcat. Below we use the test command to test this partial interaction. We find that this interaction is significant.
test _Ico1Xme1 _Ico1Xme2
( 1) _Ico1Xme1 = 0.0
( 2) _Ico1Xme2 = 0.0
F( 2, 391) = 5.78
Prob > F = 0.0033
Likewise to compare groups 2 and 3 on collcat by mealcat, we test the two terms of the interaction that involve the comparison of groups 2 and 3 on collcat. We find that this comparison is also significant.
test _Ico2Xme1 _Ico2Xme2
( 1) _Ico1Xme1 = 0.0
( 2) _Ico2Xme2 = 0.0
F( 2, 391) = 7.11
Prob > F = 0.0009
6.4.2 Coding of partial interactions
The terms _Ico1Xme1 and _Ico1Xme2 are just the product of their respective main effects. The coding for mealcat is really irrelevant, as long as some form of coding is used that sums to 0. Below you can see that _Ico1Xme1 is just _Icollcat_1 * _Imealcat_1.
tablist collcat mealcat _Icollcat_1 _Imealcat_1 _Ico1Xme1, sort(v)
collcat mealcat _Icollca~1 _Imealca~1 _Ico1Xme1 Freq
1 1 .66666667 .66666667 .44444444 35
1 2 .66666667 -.33333333 -.22222222 20
1 3 .66666667 -.33333333 -.22222222 74
2 1 -.33333333 .66666667 -.22222222 43
2 2 -.33333333 -.33333333 .11111111 43
2 3 -.33333333 -.33333333 .11111111 48
3 1 -.33333333 .66666667 -.22222222 53
3 2 -.33333333 -.33333333 .11111111 69
3 3 -.33333333 -.33333333 .11111111 15
And you can see that _Ico1Xme2 is just _Icollcat_1 * _Imealcat_2.
tablist collcat mealcat _Icollcat_1 _Imealcat_2 _Ico1Xme2, s(v)
collcat mealcat _Icollca~1 _Imealca~2 _IcolXme~2 Freq
1 1 .66666667 .33333333 .22222222 35
1 2 .66666667 .33333333 .22222222 20
1 3 .66666667 -.66666667 -.44444444 74
2 1 -.33333333 .33333333 -.11111111 43
2 2 -.33333333 .33333333 -.11111111 43
2 3 -.33333333 -.66666667 .22222222 48
3 1 -.33333333 .33333333 -.11111111 53
3 2 -.33333333 .33333333 -.11111111 69
3 3 -.33333333 -.66666667 .22222222 15
6.5. Interaction contrasts
Above we saw that a partial interaction allows you to apply contrast coefficients to one of the terms in a two-way interaction. An interaction contrast allows you to apply contrast coefficients to both of the terms in a two-way interaction.
For example, with respect to collcat say that we wish to compare groups 2 and 3, and with respect to mealcat we wish to compare groups 1 and 2. The table of this looks like this below.
| -1 | 1 | 0 | ||
| Collcat low | Collcat Med | Collcat High | ||
| 0 | Mealcat Low | |||
| -1 | Mealcat Med | |||
| 1 | Mealcat High | |||
We also would like to form a second interaction contrast that also compares groups 2 and 3 with respect to collcat, and compares groups 2 and 3 on mealcat. A table of this comparison is shown below.
| 0 | -1 | 1 | ||
| Collcat low | Collcat Med | Collcat High | ||
| 0 | Mealcat Low | |||
| -1 | Mealcat Med | |||
| 1 | Mealcat High | |||
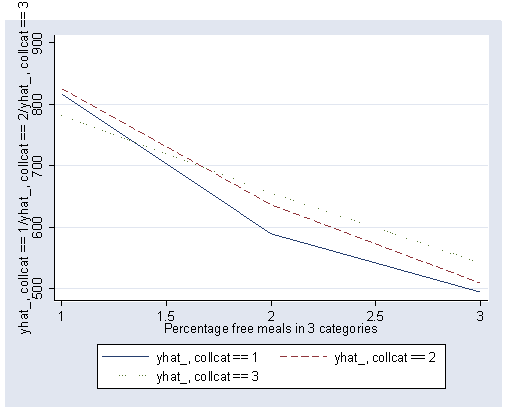
If we look at the graph of the predicted values (repeated below) we constructed before, it compares the dashed and dotted lines (collcat 2 versus 3) by mealcat 1 versus 2, and then again by mealcat 2 versus 3.
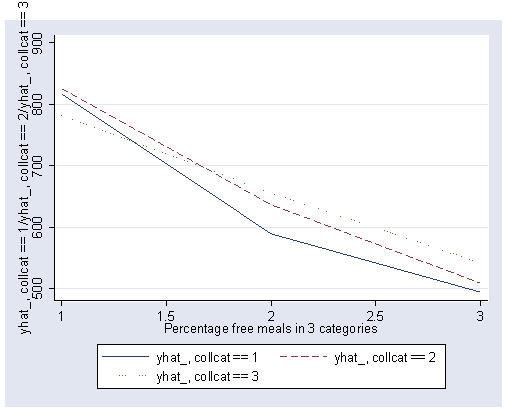
6.5.1 Analyzing interaction contrasts using xi3 and regress
Because we would like to compare groups 1 versus 2, and then groups 2 versus 3 on mealcat, this implies forward difference coding for mealcat (which will compare 1 versus 2, then 2 versus 3). For collcat we wish to compare groups 2 and 3, so we can use helmert coding for that comparison as we did above (since this will compare 1 versus 2 and 3, then 2 versus 3).
xi3: regress api00 h.collcat*a.mealcat
h.collcat _Icollcat_1-3 (naturally coded; _Icollcat_3 omitted)
a.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icollcat_1 | -25.04078 8.345388 -3.00 0.003 -41.44823 -8.633334
_Icollcat_2 | -2.810937 9.329377 -0.30 0.763 -21.15296 15.53108
_Imealcat_1 | 181.0414 9.077126 19.94 0.000 163.1953 198.8874
_Imealcat_2 | 112.3689 9.907594 11.34 0.000 92.89009 131.8477
_Ico1Xme1 | 69.7844 21.4752 3.25 0.001 27.56308 112.0057
_Ico1Xme2 | -25.40675 21.06663 -1.21 0.229 -66.82479 16.01128
_Ico2Xme1 | 62.53325 19.33438 3.23 0.001 24.5209 100.5456
_Ico2Xme2 | 13.86697 24.21132 0.57 0.567 -33.73369 61.46763
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
If we are not sure what term we want to use, we can use the describe command to show the labels for the interaction terms.
describe _Ico1Xme* _Ico2Xme*
storage display value variable name type format label variable label ------------------------------------------------------------------------------- _Ico1Xme1 double %10.0g collcat(1 vs. 2+) & mealcat(1 vs. 2) _Ico1Xme2 double %10.0g collcat(1 vs. 2+) & mealcat(2 vs. 3) _Ico2Xme1 double %10.0g collcat(2 vs. 3) & mealcat(1 vs. 2) _Ico2Xme2 double %10.0g collcat(2 vs. 3) & mealcat(2 vs. 3)
The first interaction comparison of interest is tested by _Ico12Xme1 , and this term is significant. As we expect, the red and green lines are not parallel when we compare mealcat 1 and 2.
The second interaction comparison of interest is tested by _Ico2Xme2 , and this term is not significant. Looking at the graph, we can see that the red and green lines are mostly parallel between mealcat 2 and 3.
6.5.2 Coding of interaction contrasts
The term _Ico2Xme1 is just the product of the respective main effects, as shown below.
tablist collcat mealcat _Icollcat_2 _Imealcat_1 _Ico1Xme1 , sort(v)
collcat mealcat _Icoll~2 _Imealca~1 _Ico2Xme1 Freq
1 1 0 .66666667 0 35
1 2 0 -.33333333 0 20
1 3 0 -.33333333 0 74
2 1 .5 .66666667 .3333333 43
2 2 .5 -.33333333 -.1666667 43
2 3 .5 -.33333333 -.1666667 48
3 1 -.5 .66666667 -.3333333 53
3 2 -.5 -.33333333 .1666667 69
3 3 -.5 -.33333333 .1666667 15
6.6 Computing adjusted means
6.6.1 Computing adjusted means via anova
First, we show how you can compute adjusted means using the anova command. We use the same model that we have been using, including mealcat, collcat and the interaction of these two variables.
anova api00 collcat mealcat collcat*mealcat emer, contin(emer)
Number of obs = 400 R-squared = 0.7930
Root MSE = 65.4617 Adj R-squared = 0.7882
Source | Partial SS df MS F Prob > F
----------------+----------------------------------------------------
Model | 6402428.26 9 711380.918 166.01 0.0000
|
collcat | 34730.0899 2 17365.0449 4.05 0.0181
mealcat | 3017331.85 2 1508665.92 352.06 0.0000
collcat*mealcat | 96789.1156 4 24197.2789 5.65 0.0002
emer | 158713.455 1 158713.455 37.04 0.0000
|
Residual | 1671243.73 390 4285.24034
----------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
After performing the anova, we can then use the adjust command to get adjusted means broken down by collcat and mealcat. These adjusted means compute the mean that would be expected if every school in the sample were at the mean for the variable emer. Note that it is possible to compute adjusted means with emer at other values besides the mean, for example if we had put emer=50 it would have computed means adjusting each school as though it had a mean of 50.
adjust emer , by(collcat mealcat)
--------------------------------------------------------------------------
Dependent variable: api00 Command: anova
Covariate set to mean: emer = 12.6575
--------------------------------------------------------------------------
-------------------------------------
|Percentage free meals in 3
| categories
collcat | 1 2 3
----------+--------------------------
1 | 797.56 596.973 509.872
2 | 812.55 636.405 523.885
3 | 767.935 652.976 550.462
-------------------------------------
Key: Linear Prediction
6.6.2 Computing adjusted means via regress
Now we illustrate how to get the same adjusted means if you were to to the analysis via the regress command. First, we perform the regression analysis that is equivalent to the anova command above.
xi3: regress api00 g.collcat*g.mealcat emer
g.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted)
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 9, 390) = 166.01
Model | 6402428.26 9 711380.918 Prob > F = 0.0000
Residual | 1671243.73 390 4285.24034 R-squared = 0.7930
-------------+------------------------------ Adj R-squared = 0.7882
Total | 8073672 399 20234.7669 Root MSE = 65.462
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icollcat_2 | 22.81146 8.713721 2.62 0.009 5.679711 39.9432
_Icollcat_3 | 22.32251 9.588069 2.33 0.020 3.471742 41.17328
_Imealcat_2 | -163.8973 9.131088 -17.95 0.000 -181.8497 -145.945
_Imealcat_3 | -264.6091 10.20556 -25.93 0.000 -284.6739 -244.5443
_Ico2Xme2 | 24.44231 23.26715 1.05 0.294 -21.30242 70.18704
_Ico2Xme3 | -.9774027 19.2525 -0.05 0.960 -38.82908 36.87428
_Ico3Xme2 | 85.62852 22.04718 3.88 0.000 42.28233 128.9747
_Ico3Xme3 | 70.21457 23.47354 2.99 0.003 24.06405 116.3651
emer | -2.00997 .3302709 -6.09 0.000 -2.659304 -1.360636
_cons | 675.2877 5.55622 121.54 0.000 664.3638 686.2116
------------------------------------------------------------------------------
To create the adjusted means we wish to assume that all of the schools are at the average on the variable emer. We do this by assigning the average of emer to the variable emer, but first making a copy of emer as temer so we don’t destroy the contents of this variable.
rename emer temer egen emer = mean(temer)
Now we create yhat as the predicted value. Since the value of emer is set to the mean of emer, this will be the predicted value assuming that all schools are at the average for emer.
predict yhat
Now, we can look at the average of yhat broken down by collcat and mealcat, which you can see corresponds to the adjusted means that we found with the adjust command following the anova command above.
table collcat mealcat, contents(yhat)
Means of Fitted values
| Percentage free meals in 3
| categories
collcat | 1 2 3 | Total
-----------+---------------------------------+----------
1 | 797.56042 596.97284 509.87225 | 601.43115
2 | 812.55023 636.40497 523.88464 | 652.62341
3 | 767.93524 652.97614 550.46161 | 686.22515
-----------+---------------------------------+----------
Total | 790.49498 639.0926 519.22579 | 647.6225
We then drop the variable emer and yhat since we no longer need these variables, and rename temer back to emer so the emer variable is back to the way it was before this process.
drop yhat emer rename temer emer
6.63 Computing Adjusted means via postgr3
The postgr command can be used to simplify the process of computing adjusted means (i.e. predicted values when holding other variables constant). Let’s assume that you have run the same regression as shown above
. xi3: regress api00 g.collcat*g.mealcat emer <output omitted to save space>
You can then show the graph of adjusted means and table of adjusted means using postgr3 as shown below. Below we show just the able of adjusted means, and you can see that they correspond to those computed above. We should stress that it is important to use the xi3 command (rather than xi) before using postgr3 because then postgr3 knows which variables should be held constant (in this example emer) and which variables should not be held constant (in this example, _Imealcat_2 through _Ico3Xme3).
. postgr3 mealcat, by(collcat) connect(solid dash dot) table2
Variables left asis: _Imealcat_2 _Imealcat_3 _Icollcat_2 _Icollcat_3
> _Ico2Xme2 _Ico2Xme3 _Ico3Xme2 _Ico3Xme3
Holding emer constant at 12.6575
----------------------------------------------------------------------
| Percentage free meals in 3 categories
collcat | 0-46% free meals 47-80% free meals 81-100% free meals
----------+-----------------------------------------------------------
1 | 797.5604 596.9728 509.8723
2 | 812.5502 636.405 523.8846
3 | 767.9352 652.9761 550.4616
----------------------------------------------------------------------
6.7 More details on meaning of coefficients
So far we have discussed a variety of techniques that you can use to help interpret interactions of categorical variables in regression, but we have not gone into great detail about the meaning of the coefficients in these analyses. Let’s consider this further. Consider the analysis below using collcat and mealcat, using simple contrasts on both of these variables.
xi3: regress api00 g.collcat*g.mealcat
g.collcat _Icollcat_1-3 (naturally coded; _Icollcat_1 omitted)
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 8, 391) = 166.76
Model | 6243714.81 8 780464.351 Prob > F = 0.0000
Residual | 1829957.19 391 4680.19741 R-squared = 0.7733
-------------+------------------------------ Adj R-squared = 0.7687
Total | 8073672 399 20234.7669 Root MSE = 68.412
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icollcat_2 | 23.63531 9.105331 2.60 0.010 5.733782 41.53685
_Icollcat_3 | 26.44625 9.995129 2.65 0.008 6.795331 46.09717
_Imealcat_2 | -181.0414 9.077126 -19.94 0.000 -198.8874 -163.1953
_Imealcat_3 | -293.4103 9.449459 -31.05 0.000 -311.9884 -274.8322
_Ico2Xme2 | 38.51777 24.19532 1.59 0.112 -9.051422 86.08697
_Ico2Xme3 | 6.177537 20.08262 0.31 0.759 -33.3059 45.66097
_Ico3Xme2 | 101.051 22.88808 4.42 0.000 56.05191 146.0501
_Ico3Xme3 | 82.57776 24.43941 3.38 0.001 34.52867 130.6268
_cons | 650.0883 3.871885 167.90 0.000 642.4759 657.7006
------------------------------------------------------------------------------
We can produce the adjusted means as shown below. These will be useful for interpreting the meaning of the coefficients.
predict yhat table collcat mealcat, contents(mean yhat)
Means of Fitted values
| Percentage free meals in 3
| categories
collcat | 1 2 3 | Total
-----------+---------------------------------+----------
1 | 816.91431 589.34998 493.91891 | 596.34884
2 | 825.65118 636.60468 508.83334 | 651.50002
3 | 782.15094 655.6377 541.73334 | 692.1095
-----------+---------------------------------+----------
Total | 805.71757 639.39395 504.37956 | 647.62251
We drop the variable yhat since we no longer need it in case we wish to use this variable name again.
drop yhat
Let’s consider the meaning of the coefficient for _Icollcat_2. The coding for this variable compares group 2 versus group 1; hence, this coefficient corresponds to mean(collcat2) – mean(collcat1). Note that these are the unweighted means, so we compute the mean for collcat2 as the mean of the three cells corresponding to collcat2, i.e., (825.651+636.605+508.833)/3 . If we compare the result below to the coefficient for _Icollcat_2 we see that they are the same.
display (825.651+636.605+508.833)/3 - (816.914+589.35+493.919)/3
23.635333
Likewise, the coefficient for _Icollcat_3 is mean(collcat3) – mean(collcat1), computed below. The value below corresponds to the coefficient for _Icollcat_3.
display (782.151+655.638+541.733)/3 - (816.914+589.35+493.919)/3
26.446333
Likewise, the coefficient for _Imealcat_2 works out to be mean(mealcat2) – mean(mealcat1), see below.
display (589.35+636.605+655.638)/3 - (816.914+825.651+782.151)/3
-181.041
And the coefficient for _Imealcat_3 is mean(mealcat3) – mean(mealcat1), see below.
display (493.919+508.833+541.733)/3 - (816.914+825.651+782.151)/3
-293.41033
To get the meaning of the coefficients for the interaction terms, we need to multiply the contrast coding of the main effects that created the interaction terms. For example, the term _Ico2Xme2 is the product of _Icollcat_2 and _Imealcat_2. We can form a 3 by 3 table showing the coding for _Icollcat_2 on the left, and _Imealcat_2 along the top, and then multiply these terms together and place the products in the cells of the table, see below
| -1 | 1 | 0 | ||
| Collcat low | Collcat Med | Collcat High | ||
| -1 | Mealcat Low | 1 | -1 | 0 |
| 1 | Mealcat Med | -1 | 1 | 0 |
| 0 | Mealcat High | 0 | 0 | 0 |
We then can multiply these terms in the cells by the means of the cells and we get the value for the coefficient for _Ico2Xme2. In other words, we see that this coefficient corresponds to the means of cells (1,2) and (2,1) minus cells (1,1) and (2,2).
display ( 816.914 - 589.35 - 825.651 + 636.605 )
38.518
We can go through the same process to verify the meaning of the coefficients for the other three interaction terms. We verify that _Ico2Xme3 is 6.177.
display ( 816.914 - 493.919 - 825.651 + 508.833)
6.177
We also verify that _Ico3Xme2 is 101.051.
display ( 816.914 - 589.35 - 782.151 + 655.638 )
101.051
And we verify that _Ico3Xme3 is 82.577.
display ( 816.914 - 493.919 - 782.151 + 541.733 )
82.577
6.8 Simple effects via dummy coding versus effect coding
You may wonder why we have gone to the effort of using xi3 for creating and testing these effects instead of just using dummy coding like we would get with the xi command. Let’s compare how to get simple effects using the xi3 command via effect coding to how we would get simple effects using xi with dummy coding. We hope to show that it is much easier to use effect coding via xi3 and that the interpretation of the coefficients is much more intuitive.
6.8.1 Example 1. Simple effects of yr_rnd at levels of mealcat
Let’s use an example from Chapter 3 (section 3.5). In that example we looked at an analysis using mealcat and yr_rnd and the interaction of these two variables. First, we look at how to do a simple effects analysis looking at the simple effects of yr_rnd at each level of mealcat using the xi3 command with effect coding. To make our results correspond to those from Chapter 3, we will make group 3 of mealcat the reference category.
char mealcat[omit] 3 xi3 : regress api00 g.yr_rnd@g.mealcat
g.yr_rnd _Iyr_rnd_0-1 (naturally coded; _Iyr_rnd_0 omitted)
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 261.61
Model | 6204727.82 5 1240945.56 Prob > F = 0.0000
Residual | 1868944.18 394 4743.51314 R-squared = 0.7685
-------------+------------------------------ Adj R-squared = 0.7656
Total | 8073672 399 20234.7669 Root MSE = 68.873
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 267.8108 14.61559 18.32 0.000 239.0765 296.5451
_Imealcat_2 | 114.6572 11.12812 10.30 0.000 92.77923 136.5351
_Iyr1Wme1 | -74.25691 26.75629 -2.78 0.006 -126.8599 -21.65397
_Iyr1Wme2 | -51.74017 18.88854 -2.74 0.006 -88.87511 -14.60523
_Iyr1Wme3 | -33.49254 11.77129 -2.85 0.005 -56.63492 -10.35015
_cons | 632.2356 5.800477 109.00 0.000 620.8318 643.6393
------------------------------------------------------------------------------
Now we can obtain the simple effect of yr_rnd at mealcat=1 by inspecting the coefficient for _Iyr1Wme1, the simple effect of yr_rnd at mealcat=2 by inspecting the coefficient for _Iyr1Wme2 and the simple effect of yr_rnd at mealcat=3 by inspecting the coefficient for _Iyr1Wme3.
Now let’s perform the same analysis using xi with dummy coding. Again, we will explicitly make the third group for mealcat to be the omitted category.
char mealcat[omit] 3 xi : regress api00 i.mealcat*yr_rnd
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
i.meal~t*yr_rnd _ImeaXyr_rn_# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 261.61
Model | 6204727.82 5 1240945.56 Prob > F = 0.0000
Residual | 1868944.18 394 4743.51314 R-squared = 0.7685
-------------+------------------------------ Adj R-squared = 0.7656
Total | 8073672.00 399 20234.7669 Root MSE = 68.873
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 288.1929 10.44284 27.60 0.000 267.6623 308.7236
_Imealcat_2 | 123.781 10.55185 11.73 0.000 103.036 144.5259
yr_rnd | -33.49254 11.77129 -2.85 0.005 -56.63492 -10.35015
_ImeaXyr_r~1 | -40.76438 29.23118 -1.39 0.164 -98.23297 16.70422
_ImeaXyr_r~2 | -18.24763 22.25624 -0.82 0.413 -62.00347 25.5082
_cons | 521.4925 8.414197 61.98 0.000 504.9502 538.0349
------------------------------------------------------------------------------
In order to form a test of simple main effects we need to make a table like the one shown below that relates the means of the cells to the coefficients in the regression. Please see Chapter 3, section 3.5 for information on how this table was constructed.
mealcat=1 mealcat=2 mealcat=3
-------------------------------------------------
yr_rnd=0 _cons _cons _cons
+BImealcat1 +BImealcat2
-------------------------------------------------
yr_rnd=1 _cons _cons _cons
+Byr_rnd +Byr_rnd +Byr_rnd
+BImealcat1 +BImealcat2
+B_ImeaXyr_rn_1 +B_ImeaXyr_rn_2
Let’s start by looking at how to get the simple effect of yr_rnd when mealcat is 3. Looking at the table above, we can see that we would want to compare _cons with _cons + Byr_rnd. We can do this with the lincom command as shown below.
lincom _cons - (_cons + yr_rnd)
( 1) - yr_rnd = 0.0
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 33.49254 11.77129 2.85 0.005 10.35015 56.63492
------------------------------------------------------------------------------
We see that _cons drops out, yielding just yr_rnd. Instead, we can use the test command to test whether the coefficient for yr_rnd is 0. Note that this result corresponds to the result we found with the xi3 command also testing the simple effect of yr_rnd when mealcat is 3.
test yr_rnd=0
( 1) yr_rnd = 0.0
F( 1, 394) = 8.10
Prob > F = 0.0047
Note that the coefficient for yr_rnd corresponds to the test of the effect of yr_rnd when all other variables are set to 0 (the reference category), in other words, when mealcat is set to the reference category. You may be tempted to interpret the coefficient for yr_rnd as the overall difference between year round schools and non-year round schools, but in this example we see that it really corresponds to the simple effect of yr_rnd. When using dummy coding people commonly misinterpret the lower order effects to refer to overall effects rather than simple effects.
Now let’s look at the simple effect of yr_rnd when mealcat=1. Looking at the table above we see that this involves the comparison of the coefficients for yr_rnd=1 versus yr_rnd=0 when mealcat=1, i.e., comparing _cons + yr_rnd + _Imealcat_1 + _ImeaXyr_rn_1 versus _cons + _Imealcat_1. Removing the terms that drop out we can do the test command below.
test yr_rnd + _ImeaXyr_rn_1=0
( 1) yr_rnd + _ImeaXyr_rn_1 = 0.0
F( 1, 394) = 7.70
Prob > F = 0.0058
We can likewise obtain the effect of yr_rnd when mealcat is 2, as shown below.
test yr_rnd + _ImeaXyr_rn_2=0
( 1) yr_rnd + _ImeaXyr_rn_2 = 0.0
F( 1, 394) = 7.50
Prob > F = 0.0064
These examples illustrate that it is more complicated to form simple effects when using dummy coding, and also that the interpretation of lower order effects when using dummy coding may not have the meaning that you would expect.
6.8.2 Example 2. Simple effects of mealcat at levels of yr_rnd
Example 1 looked at simple effects for yr_rnd, a variable with only two levels In this example, let’s consider the simple effects of mealcat at each level of yr_rnd. Because mealcat has more than two levels, we can see what is required for doing tests of simple effects for variables with more than two levels.
First, let’s show how to get these simple effects using the xi3 command using effect coding.
xi3 : regress api00 g.mealcat@g.yr_rnd
g.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
g.yr_rnd _Iyr_rnd_0-1 (naturally coded; _Iyr_rnd_0 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 261.61
Model | 6204727.82 5 1240945.56 Prob > F = 0.0000
Residual | 1868944.18 394 4743.51314 R-squared = 0.7685
-------------+------------------------------ Adj R-squared = 0.7656
Total | 8073672 399 20234.7669 Root MSE = 68.873
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iyr_rnd_1 | -53.16321 11.60095 -4.58 0.000 -75.97072 -30.3557
_Ime1Wyr0 | 288.1929 10.44284 27.60 0.000 267.6623 308.7236
_Ime1Wyr1 | 247.4286 27.30218 9.06 0.000 193.7524 301.1048
_Ime2Wyr0 | 123.781 10.55185 11.73 0.000 103.036 144.5259
_Ime2Wyr1 | 105.5333 19.59588 5.39 0.000 67.00776 144.0589
_cons | 632.2356 5.800477 109.00 0.000 620.8318 643.6393
------------------------------------------------------------------------------
We can get the simple effect of mealcat at yr_rnd = 0 just as we did earlier in this chapter.
test _Ime1Wyr0 _Ime2Wyr0
( 1) _Ime1Wyr0 = 0
( 2) _Ime2Wyr0 = 0
F( 2, 394) = 411.46
Prob > F = 0.0000
And we likewise get the simple effect of mealcat at yr_rnd = 1 as shown below.
test _Ime1Wyr1 _Ime2Wyr1
( 1) _Ime1Wyr1 = 0
( 2) _Ime2Wyr1 = 0
F( 2, 394) = 50.19
Prob > F = 0.0000
We can now test the simple effects of mealcat at each level of yr_rnd via dummy coding.
xi : regress api00 i.mealcat*yr_rnd
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
i.meal~t*yr_rnd _ImeaXyr_rn_# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 261.61
Model | 6204727.82 5 1240945.56 Prob > F = 0.0000
Residual | 1868944.18 394 4743.51314 R-squared = 0.7685
-------------+------------------------------ Adj R-squared = 0.7656
Total | 8073672.00 399 20234.7669 Root MSE = 68.873
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 288.1929 10.44284 27.60 0.000 267.6623 308.7236
_Imealcat_2 | 123.781 10.55185 11.73 0.000 103.036 144.5259
yr_rnd | -33.49254 11.77129 -2.85 0.005 -56.63492 -10.35015
_ImeaXyr_r~1 | -40.76438 29.23118 -1.39 0.164 -98.23297 16.70422
_ImeaXyr_r~2 | -18.24763 22.25624 -0.82 0.413 -62.00347 25.5082
_cons | 521.4925 8.414197 61.98 0.000 504.9502 538.0349
------------------------------------------------------------------------------
The simple effect of mealcat when yr_rnd is 0 requires two test statements since it is a 2 degree of freedom test. We can do this by testing mean(mealcat1) = mean(mealcat2) and also testing mean(mealcat2) = mean(mealcat3). We can look at the table above and see that mean(mealcat1) = mean(mealcat2) is _Imealcat_1– _Imealcat_2 (after _cons drops out) and mean(mealcat2) = mean(mealcat3) is _Imealcat_2 after _cons drops out. So, we can perform this test using the two test commands below.
test _Imealcat_1- _Imealcat_2=0
( 1) _Imealcat_1 - _Imealcat_2 = 0.0
F( 1, 394) = 343.05
Prob > F = 0.0000
test _Imealcat_2, accum
( 1) _Imealcat_1 - _Imealcat_2 = 0.0
( 2) _Imealcat_2 = 0.0
F( 2, 394) = 411.46
Prob > F = 0.0000
Note that the effects _Imealcat_1 and _Imealcat_2 do not correspond to overall effects of the variable mealcat but are the simple effects when yr_rnd is set to 0, the reference level. Again we see that the terms that we might be tempted to call main effects and think of as overall effects really are simple effects when dummy coding is used.
The second test command uses the accum option to accumulate the tests to get the 2 degree of freedom test that corresponds to the simple effect of mealcat when yr_rnd is 0.
Likewise, we can look at the table above to form the comparisons needed to obtain the simple effects of mealcat when yr_rnd is 1.
test _Imealcat_1+ _ImeaXyr_rn_1- _Imealcat_2- _ImeaXyr_rn_2=0
( 1) _Imealcat_1 - _Imealcat_2 + _ImeaXyr_rn_1 - _ImeaXyr_rn_2 = 0.0
F( 1, 394) = 20.26
Prob > F = 0.0000
test _Imealcat_2+ _ImeaXyr_rn_2=0, accum
( 1) _Imealcat_1 - _Imealcat_2 + _ImeaXyr_rn_1 - _ImeaXyr_rn_2 = 0.0
( 2) _Imealcat_2 + _ImeaXyr_rn_2 = 0.0
F( 2, 394) = 50.19
Prob > F = 0.0000
Using this example we hoped to illustrate that when performing simple effects for a variable with more than two levels can be quite tricky and requires constructing multiple test commands, one test command for every degree of freedom in the simple effect. As you can see, constructing these terms can be very tricky and possibly error prone. Without a method for double checking results, it is very possible to make a mistake when constructing terms and form the wrong comparison. By comparison, using effect coding with xi3, forming comparisons can be much easier and the interpretation of the lower order effects is much more intuitive. The lower order effects do correspond to the overall effects of the variable, for example the effect of yr_rnd, when using effect coding, does correspond to the overall unweighted mean for the year round schools compared to the non-year round schools.