Chapter Outline 3.0 Regression with Categorical Predictors 3.1 Regression with a 0/1 variable 3.2 Regression with a 1/2 variable 3.3 Regression with a 1/2/3 variable 3.4 Regression with multiple categorical predictors 3.5 Categorical predictor with interactions 3.6 Continuous and Categorical variables 3.7 Interactions of Continuous by 0/1 Categorical variables 3.8 Continuous and Categorical variables, interaction with 1/2/3 variable 3.9 Summary 3.10 Self assessment 3.11 For more information
Please note: This page makes use of the program xi3 which is no longer being maintained and has been from our archives. References to xi3 will be left on this page because they illustrate specific principles of coding categorical variables.
3.0 Introduction
In the previous two chapters, we have focused on regression analyses using continuous variables. However, it is possible to include categorical predictors in a regression analysis, but it requires some extra work in performing the analysis and extra work in properly interpreting the results. This chapter will illustrate how you can use Stata for including categorical predictors in your analysis and describe how to interpret the results of such analyses. Stata has some great tools that really ease the process of including categorical variables in your regression analysis, and we will emphasize the use of these timesaving tools.
This chapter will use the elemapi2 data that you have seen in the prior chapters. We will focus on four variables api00, some_col, yr_rnd and mealcat, which takes meals and breaks it up into 3 categories. Let’s have a quick look at these variables.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2
describe api00 some_col yr_rnd mealcat
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
api00 int %6.0g api 2000
some_col byte %4.0f parent some college
yr_rnd byte %4.0f yr_rnd year round school
mealcat byte %18.0g mealcat Percentage free meals in 3
categories
The variable api00 is a measure of the performance of the schools. Below we see the codebook information for api00
codebook api00
api00 ---------------------------------------------------------------- api 2000
type: numeric (int)
range: [369,940] units: 1
unique values: 271 coded missing: 0 / 400
mean: 647.622
std. dev: 142.249
percentiles: 10% 25% 50% 75% 90%
465.5 523.5 643 762.5 850
The variable some_col is a continuous variable that measures the percentage of the parents in the school who have attended college, and the codebook information is shown below.
codebook some_col
some_col -------------------------------------------------- parent some college
type: numeric (byte)
range: [0,67] units: 1
unique values: 49 coded missing: 0 / 400
mean: 19.7125
std. dev: 11.3369
percentiles: 10% 25% 50% 75% 90%
2.5 12 19 28 34
The variable yr_rnd is a categorical variable that is coded 0 if the school is not year round, and 1 if year round, see below.
codebook yr_rnd
yr_rnd ------------------------------------------------------ year round school
type: numeric (byte)
label: yr_rnd
range: [0,1] units: 1
unique values: 2 coded missing: 0 / 400
tabulation: Freq. Numeric Label
308 0 No
92 1 Yes
The variable meals is the percentage of students who are receiving state sponsored free meals and can be used as an indicator of poverty. This was broken into 3 categories (to make equally sized groups) creating the variable mealcat. The codebook information for mealcat is shown below.
codebook mealcat
mealcat ----------------------------------------------------------- (unlabeled)
type: numeric (float)
label: mealcat
range: [1,3] units: 1
unique values: 3 coded missing: 0 / 400
tabulation: Freq. Numeric Label
131 1 0-46% free meals
132 2 47-80% free meals
137 3 81-100% free meals
3.1 Regression with a 0/1 variable
The simplest example of a categorical predictor in a regression analysis is a 0/1 variable, also called a dummy variable. Let’s use the variable yr_rnd as an example of a dummy variable. We can include a dummy variable as a predictor in a regression analysis as shown below.
regress api00 yr_rnd
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 1, 398) = 116.24
Model | 1825000.56 1 1825000.56 Prob > F = 0.0000
Residual | 6248671.43 398 15700.1795 R-squared = 0.2260
-------------+------------------------------ Adj R-squared = 0.2241
Total | 8073672.00 399 20234.7669 Root MSE = 125.30
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -160.5064 14.8872 -10.78 0.000 -189.7737 -131.239
_cons | 684.539 7.13965 95.88 0.000 670.5028 698.5751
------------------------------------------------------------------------------
This may seem odd at first, but this is a legitimate analysis. But what does this mean? Let’s go back to basics and write out the regression equation that this model implies.
api00 = _cons + Byr_rnd * yr_rnd
where _cons is the intercept (or constant) and we use Byr_rnd to represent the coefficient for variable yr_rnd. Filling in the values from the regression equation, we get
api00 = 684.539 + -160.5064 * yr_rnd
If a school is not a year-round school (i.e. yr_rnd is 0) the regression equation would simplify to
api00 = constant + 0 * Byr_rnd api00 = 684.539 + 0 * -160.5064 api00 = 684.539
If a school is a year-round school, the regression equation would simplify to
api00 = constant + 1 * Byr_rnd api00 = 684.539 + 1 * -160.5064 api00 = 524.0326
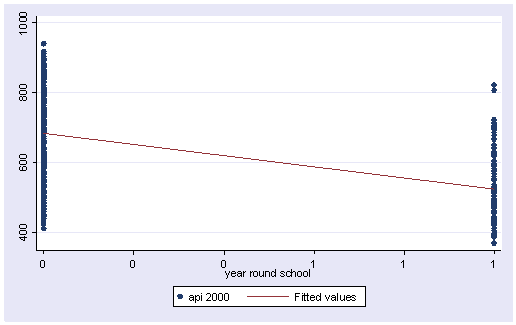
We can graph the observed values and the predicted values using the scatter command as shown below. Although yr_rnd only has 2 values, we can still draw a regression line showing the relationship between yr_rnd and api00. Based on the results above, we see that the predicted value for non-year round schools is 684.539 and the predicted value for the year round schools is 524.032, and the slope of the line is negative, which makes sense since the coefficient for yr_rnd was negative (-160.5064).
twoway (scatter api00 yr_rnd) (lfit api00 yr_rnd)
Let’s compare these predicted values to the mean api00 scores for the year-round and non-year-round schools.
tabulate yr_rnd, sum(api00)
year round | Summary of api 2000
school | Mean Std. Dev. Freq.
------------+------------------------------------
No | 684.53896 132.11253 308
Yes | 524.03261 98.916043 92
------------+------------------------------------
Total | 647.6225 142.24896 400
As you see, the regression equation predicts that the value of api00 will be the mean value, depending on whether a school is a year round school or non-year round school.
Let’s relate these predicted values back to the regression equation. For the non-year-round schools, their mean is the same as the intercept (684.539). The coefficient for yr_rnd is the amount we need to add to get the mean for the year-round schools, i.e., we need to add -160.5064 to get 524.0326, the mean for the non year-round schools. In other words, Byr_rnd is the mean api00 score for the year-round schools minus the mean api00 score for the non year-round schools, i.e., mean(year-round) – mean(non year-round).
It may be surprising to note that this regression analysis with a single dummy variable is the same as doing a t-test comparing the mean api00 for the year-round schools with the non year-round schools (see below). You can see that the t value below is the same as the t value for yr_rnd in the regression above. This is because Byr_rnd compares the year-rounds and non year-rounds (since the coefficient is mean(year round)-mean(non year-round)).
ttest api00, by(yr_rnd)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
No | 308 684.539 7.52781 132.1125 669.7263 699.3516
Yes | 92 524.0326 10.31271 98.91604 503.5477 544.5175
---------+--------------------------------------------------------------------
combined | 400 647.6225 7.112448 142.249 633.6399 661.6051
---------+--------------------------------------------------------------------
diff | 160.5064 14.8872 131.239 189.7737
------------------------------------------------------------------------------
Degrees of freedom: 398
Ho: mean(No) - mean(Yes) = diff = 0
Ha: diff < 0 Ha: diff ~= 0 Ha: diff > 0
t = 10.7815 t = 10.7815 t = 10.7815
P < t = 1.0000 P > |t| = 0.0000 P > t = 0.0000
Since a t-test is the same as doing an anova, we can get the same results using the anova command as well.
anova api00 yr_rnd
Number of obs = 400 R-squared = 0.2260
Root MSE = 125.30 Adj R-squared = 0.2241
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 1825000.56 1 1825000.56 116.24 0.0000
|
yr_rnd | 1825000.56 1 1825000.56 116.24 0.0000
|
Residual | 6248671.43 398 15700.1795
-----------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
If we square the t-value from the t-test, we get the same value as the F-value from the anova.
di 10.7815^2 116.24074
3.2 Regression with a 1/2 variable
A categorical predictor variable does not have to be coded 0/1 to be used in a regression model. It is easier to understand and interpret the results from a model with dummy variables, but the results from a variable coded 1/2 yield essentially the same results.
Lets make a copy of the variable yr_rnd called yr_rnd2 that is coded 1/2, 1=non year-round and 2=year-round.
generate yr_rnd2=yr_rnd recode yr_rnd2 0=1 1=2 (400 changes made)
Let’s perform a regression predicting api00 from yr_rnd2.
regress api00 yr_rnd2
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 1, 398) = 116.24
Model | 1825000.56 1 1825000.56 Prob > F = 0.0000
Residual | 6248671.43 398 15700.1795 R-squared = 0.2260
-------------+------------------------------ Adj R-squared = 0.2241
Total | 8073672.00 399 20234.7669 Root MSE = 125.30
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd2 | -160.5064 14.8872 -10.78 0.000 -189.7737 -131.239
_cons | 845.0453 19.35336 43.66 0.000 806.9977 883.0929
------------------------------------------------------------------------------
Note that the coefficient for yr_rnd is the same as yr_rnd2. So, you can see that if you code yr_rnd as 0/1 or as 1/2, the regression coefficient works out to be the same. However the intercept (_cons) is a bit less intuitive. When we used yr_rnd, the intercept was the mean for the non year-rounds. When using yr_rnd2, the intercept is the mean for the non year-rounds minus Byr_rnd2, i.e., 684.539 – (-160.506) = 845.045
Note that you can use 0/1 or 1/2 coding and the results for the coefficient come out the same, but the interpretation of the constant in the regression equation is different. It is often easier to interpret the estimates for 0/1 coding.
In summary, these results indicate that the api00 scores are significantly different for the schools depending on the type of school, year round school vs. non-year round school. Non year-round schools have significantly higher API scores than year-round schools. Based on the regression results, non year- round schools have scores that are 160.5 points higher than year- round schools.
3.3 Regression with a 1/2/3 variable
3.3.1 Manually Creating Dummy Variables
Say, that we would like to examine the relationship between the amount of poverty and api scores. We don’t have a measure of poverty, but we can use mealcat as a proxy for a measure of poverty. Below we repeat the codebook info for mealcat showing the values for the three categories.
codebook mealcat
mealcat ----------------------------------------------------------- (unlabeled)
type: numeric (float)
label: mealcat
range: [1,3] units: 1
unique values: 3 coded missing: 0 / 400
tabulation: Freq. Numeric Label
131 1 0-46% free meals
132 2 47-80% free meals
137 3 81-100% free meals
You might be tempted to try including mealcat in a regression like this.
regress api00 mealcat
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 1, 398) = 1207.74
Model | 6072527.52 1 6072527.52 Prob > F = 0.0000
Residual | 2001144.48 398 5028.0012 R-squared = 0.7521
-------------+------------------------------ Adj R-squared = 0.7515
Total | 8073672.00 399 20234.7669 Root MSE = 70.908
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcat | -150.5533 4.332147 -34.75 0.000 -159.0701 -142.0365
_cons | 950.9874 9.421798 100.93 0.000 932.4647 969.5101
------------------------------------------------------------------------------
But this is looking at the linear effect of mealcat with api00, but mealcat is not an interval variable. Instead, you will want to code the variable so that all the information concerning the three levels is accounted for. You can dummy code mealcat like this.
tabulate mealcat, gen(mealcat)
mealcat | Freq. Percent Cum.
-------------------+-----------------------------------
0-46% free meals | 131 32.75 32.75
47-80% free meals | 132 33.00 65.75
81-100% free meals | 137 34.25 100.00
-------------------+-----------------------------------
Total | 400 100.00
We now have created mealcat1 that is 1 if mealcat is 1, and 0 otherwise. Likewise, mealcat2 is 1 if mealcat is 2, and 0 otherwise and likewise mealcat3 was created. We can see this below.
list mealcat mealcat1 mealcat2 mealcat3 in 1/10, nolabel
mealcat mealcat1 mealcat2 mealcat3
1. 1 1 0 0
2. 2 0 1 0
3. 3 0 0 1
4. 1 1 0 0
5. 1 1 0 0
6. 1 1 0 0
7. 1 1 0 0
8. 1 1 0 0
9. 1 1 0 0
10. 1 1 0 0
We can now use two of these dummy variables (mealcat2 and mealcat3) in the regression analysis.
regress api00 mealcat2 mealcat3
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcat2 | -166.3236 8.708331 -19.10 0.000 -183.4438 -149.2034
mealcat3 | -301.338 8.628815 -34.92 0.000 -318.3019 -284.3741
_cons | 805.7176 6.169416 130.60 0.000 793.5887 817.8464
------------------------------------------------------------------------------
We can test the overall differences among the three groups by using the test command as shown below. This shows that the overall differences among the three groups are significant.
test mealcat2 mealcat3
( 1) mealcat2 = 0.0
( 2) mealcat3 = 0.0
F( 2, 397) = 611.12
Prob > F = 0.0000
The interpretation of the coefficients is much like that for the binary variables. Group 1 is the omitted group, so _cons is the mean for group 1. The coefficient for mealcat2 is the mean for group 2 minus the mean of the omitted group (group 1). And the coefficient for mealcat3 is the mean of group 3 minus the mean of group 1. You can verify this by comparing the coefficients with the means of the groups.
tabulate mealcat, summarize(api00)
| Summary of api 2000
mealcat | Mean Std. Dev. Freq.
------------+------------------------------------
0-46% fre | 805.71756 65.668664 131
47-80% fr | 639.39394 82.13513 132
81-100% f | 504.37956 62.727015 137
------------+------------------------------------
Total | 647.6225 142.24896 400
Based on these results, we can say that the three groups differ in their api00 scores, and that in particular group2 is significantly different from group1 (because mealcat2 was significant) and group 3 is significantly different from group 1 (because mealcat3 was significant).
3.3.2 Using the xi command
We can use the xi command to do the work for us to create the indicator variables and run the regression all in one command, as shown below.
xi : regress api00 i.mealcat
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_2 | -166.3236 8.708331 -19.10 0.000 -183.4438 -149.2034
_Imealcat_3 | -301.338 8.628815 -34.92 0.000 -318.3019 -284.3741
_cons | 805.7176 6.169416 130.60 0.000 793.5887 817.8464
------------------------------------------------------------------------------
When we use xi and include the term i.mealcat in the model, Stata creates the variables _Imealcat_2 and _Imealcat_3 that are dummy variables just like mealcat2 and mealcat3 that we created before. There really is no difference between mealcat2 and _Imealcat_2.
As you can see, the results are the same as in the prior analysis. If we want to test the overall effect of mealcat we use the test command as shown below, which also gives us the same results as we found using the dummy variables mealcat2 and mealcat3.
test _Imealcat_2 _Imealcat_3
( 1) _Imealcat_2 = 0.0
( 2) _Imealcat_3 = 0.0
F( 2, 397) = 611.12
Prob > F = 0.0000
Note that if you are doing this in Stata version 6 the variables would be named Imealc_2 and Imealc_3 instead of _Imealcat_2 and _Imealcat_3. One of the improvements in Stata 7 is that variable names can be longer than 8 characters, so the names of the variables created by the xi command are easier to understand than in version 6. From this point forward, we will use the variable names that would be created in version 7.
What if we wanted a different group to be the reference group? If we create dummy variables via tabulate , generate() then we can easily choose which variable will be the omitted group, for example, let’s omit group 3.
regress api00 mealcat1 mealcat2
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcat1 | 301.338 8.628815 34.92 0.000 284.3741 318.3019
mealcat2 | 135.0144 8.61209 15.68 0.000 118.0834 151.9454
_cons | 504.3796 6.032807 83.61 0.000 492.5193 516.2398
------------------------------------------------------------------------------
With group 3 omitted, the constant is now the mean of group 3 and mealcat1 is group1-group3 and mealcat2 is group2-group3. We see that both of these coefficients are significant, indicating that group 1 is significantly different from group 3 and group 2 is significantly different from group 3.
When we use the xi command, how can we choose which group is the omitted group? By default, the first group is omitted, but say we want group 3 to be omitted. We can use the char command as shown below to tell Stata that we want the third group to be the omitted group for the variable mealcat.
char mealcat[omit] 3
Then, when we use the xi command using mealcat the mealcat=3 group will be omitted. If you save the data file, Stata will remember this for future Stata sessions.
xi : regress api00 i.mealcat
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 301.338 8.628815 34.92 0.000 284.3741 318.3019
_Imealcat_2 | 135.0144 8.61209 15.68 0.000 118.0834 151.9454
_cons | 504.3796 6.032807 83.61 0.000 492.5193 516.2398
------------------------------------------------------------------------------
You can compare and see that these results are identical to those found using mealcat1 and mealcat2 as predictors.
3.3.3 Using the anova command
We can also do this analysis using the anova command. The benefit of the anova command is that it gives us the test of the overall effect of mealcat without needing to subsequently use the test command as we did with the regress command.
anova api00 mealcat
Number of obs = 400 R-squared = 0.7548
Root MSE = 70.6122 Adj R-squared = 0.7536
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 6094197.67 2 3047098.83 611.12 0.0000
|
mealcat | 6094197.67 2 3047098.83 611.12 0.0000
|
Residual | 1979474.33 397 4986.08143
-----------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
We can see the anova test of the effect of mealcat is the same as the test command from the regress command.
We can even follow this with the anova, regress command and compare the parameter estimates with those we performed previously.
anova, regress
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 Coef. Std. Err. t P>|t| [95% Conf. Interval]
------------------------------------------------------------------------------
_cons 504.3796 6.032807 83.61 0.000 492.5193 516.2398
mealcat
1 301.338 8.628815 34.92 0.000 284.3741 318.3019
2 135.0144 8.61209 15.68 0.000 118.0834 151.9454
3 (dropped)
------------------------------------------------------------------------------
Note: the parameter estimates are the same because mealcat is coded the same way in the regress command and in the anova command, in both cases the last category (category 3) being dropped. While you can control which category is the omitted category when you use the regress command, the anova, regress command always drops the last category.
3.3.4 Other coding schemes
It is generally very convenient to use dummy coding but that is not the only kind of coding that can be used. As you have seen, when you use dummy coding one of the groups becomes the reference group and all of the other groups are compared to that group. This may not be the most interesting set of comparisons.
Say you want to compare group 1 with groups 2 and 3, and for a second comparison compare group 2 with group 3. You need to generate a coding scheme that forms these 2 comparisons. We will illustrate this using a Stata program, xi3, (an enhanced version of xi) that will create the variables you would need for such comparisons (as well as a variety of other common comparisons).
The comparisons that we have described (comparing group 1 with 2 and 3, and then comparing groups 2 and 3) correspond to Helmert comparisons (see Chapter 5 for more details). We use the h. prefix (instead of the i. prefix) to indicate that we desire Helmert comparisons on the variable mealcat. Otherwise, you see that xi3 works much like the xi command.
xi3: regress api00 h.mealcat
h.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 233.8308 7.523544 31.08 0.000 219.0398 248.6218
_Imealcat_2 | 135.0144 8.61209 15.68 0.000 118.0834 151.9454
_cons | 649.8304 3.531285 184.02 0.000 642.888 656.7727
----------------------------------------------------------------------------
If you compare the parameter estimates with the means (see below) you can verify that the coefficient for _Imealcat_1 is the mean of group 1 minus the mean of groups 2 and 3 (805.71756 – (639.39394 + 504.37956) / 2 = 233.83081) and the coefficient for _Imealcat_2 is the mean of group 2 minus group 3 (639.39 – 504.37 = 135.01). Both of these comparisons are significant, indicating that group 1 differs significantly from groups 2 and 3 combined, and group 2 differs significantly from group 3.
tabulate mealcat, sum(api00)
| Summary of api 2000
mealcat | Mean Std. Dev. Freq.
------------+------------------------------------
0-46% fre | 805.71756 65.668664 131
47-80% fr | 639.39394 82.13513 132
81-100% f | 504.37956 62.727015 137
------------+------------------------------------
Total | 647.6225 142.24896 400
And the value of _cons is the unweighted average of the means of the 3 groups.
display (805.71756 +639.39394 +504.37956)/3 649.83035
Using the coding scheme provided by xi3, we were able to form perhaps more interesting tests than those provided by dummy coding. The xi3 program can create variables according to other coding schemes, as well as custom coding schemes that you create, see help xi3 and Chapter 5 for more information.
3.4 Regression with two categorical predictors
3.4.1 Using the xi: command
Previously we looked at using yr_rnd to predict api00
regress api00 yr_rnd
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 1, 398) = 116.24
Model | 1825000.56 1 1825000.56 Prob > F = 0.0000
Residual | 6248671.43 398 15700.1795 R-squared = 0.2260
-------------+------------------------------ Adj R-squared = 0.2241
Total | 8073672.00 399 20234.7669 Root MSE = 125.30
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -160.5064 14.8872 -10.78 0.000 -189.7737 -131.239
_cons | 684.539 7.13965 95.88 0.000 670.5028 698.5751
------------------------------------------------------------------------------
And we have also looked at mealcat using the xi command
xi : regress api00 i.mealcat
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 611.12
Model | 6094197.67 2 3047098.83 Prob > F = 0.0000
Residual | 1979474.33 397 4986.08143 R-squared = 0.7548
-------------+------------------------------ Adj R-squared = 0.7536
Total | 8073672.00 399 20234.7669 Root MSE = 70.612
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 301.338 8.628815 34.92 0.000 284.3741 318.3019
_Imealcat_2 | 135.0144 8.61209 15.68 0.000 118.0834 151.9454
_cons | 504.3796 6.032807 83.61 0.000 492.5193 516.2398
------------------------------------------------------------------------------
We can include both yr_rnd and mealcat together in the same model.
xi : regress api00 i.mealcat yr_rnd
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 435.02
Model | 6194144.30 3 2064714.77 Prob > F = 0.0000
Residual | 1879527.69 396 4746.28206 R-squared = 0.7672
-------------+------------------------------ Adj R-squared = 0.7654
Total | 8073672.00 399 20234.7669 Root MSE = 68.893
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 281.6832 9.445676 29.82 0.000 263.1132 300.2531
_Imealcat_2 | 117.9458 9.188911 12.84 0.000 99.88066 136.011
yr_rnd | -42.96006 9.361761 -4.59 0.000 -61.36502 -24.55509
_cons | 526.33 7.584533 69.40 0.000 511.419 541.2409
------------------------------------------------------------------------------
We can test the overall effect of mealcat with the test command, which is significant.
test _Imealcat_1 _Imealcat_2
( 1) _Imealcat_1 = 0.0
( 2) _Imealcat_2 = 0.0
F( 2, 396) = 460.27
Prob > F = 0.0000
Because this model has only main effects (no interactions) you can interpret Byr_rnd as the difference between the year round and non-year round group. The coefficient for I_mealcat_1 (which we will call B_Imealcat_1) is the difference between mealcat=1 and mealcat=3, and B_Imealcat_2 as the difference between mealcat=2 and mealcat=3.
Let’s dig below the surface and see how the coefficients relate to the predicted values. Let’s view the cells formed by crossing yr_rnd and mealcat and number the cells from cell1 to cell6.
mealcat=1 mealcat=2 mealcat=3 yr_rnd=0 cell1 cell2 cell3 yr_rnd=1 cell4 cell5 cell6
With respect to mealcat, the group mealcat=3 is the reference category, and with respect to yr_rnd the group yr_rnd=0 is the reference category. As a result, cell3 is the reference cell. The constant is the predicted value for this cell.
The coefficient for yr_rnd is the difference between cell3 and cell6. Since this model has only main effects, it is also the difference between cell2 and cell5, or from cell1 and cell4. In other words, Byr_rnd is the amount you add to the predicted value when you go from non-year round to year round schools.
The coefficient for _Imealcat_1 is the predicted difference between cell1 and cell3. Since this model only has main effects, it is also the predicted difference between cell4 and cell6. Likewise, B_Imealcat_2 is the predicted difference between cell2 and cell3, and also the predicted difference between cell5 and cell6.
So, the predicted values, in terms of the coefficients, would be
mealcat=1 mealcat=2 mealcat=3
-----------------------------------------------
yr_rnd=0 _cons _cons _cons
+BImealcat1 +BImealcat2
-----------------------------------------------
yr_rnd=1 _cons _cons _cons
+Byr_rnd +Byr_rnd +Byr_rnd
+BImealcat1 +BImealcat2
We should note that if you computed the predicted values for each cell, they would not exactly match the means in the 6 cells. The predicted means would be close to the observed means in the cells, but not exactly the same. This is because our model only has main effects and assumes that the difference between cell1 and cell4 is exactly the same as the difference between cells 2 and 5 which is the same as the difference between cells 3 and 6. Since the observed values don’t follow this pattern, there is some discrepancy between the predicted means and observed means.
3.4.2 Using the anova command
We can run the same analysis using the anova command with just main effects
anova api00 yr_rnd mealcat
Number of obs = 400 R-squared = 0.7672
Root MSE = 68.8933 Adj R-squared = 0.7654
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 6194144.30 3 2064714.77 435.02 0.0000
|
yr_rnd | 99946.6332 1 99946.6332 21.06 0.0000
mealcat | 4369143.74 2 2184571.87 460.27 0.0000
|
Residual | 1879527.69 396 4746.28206
-----------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
Note that we get the same information that we do from the xi : regress command, followed by the test command. The anova command automatically provides the information provided by the test command. If we like, we can also request the parameter estimates later just by doing this.
anova, regress
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 435.02
Model | 6194144.30 3 2064714.77 Prob > F = 0.0000
Residual | 1879527.69 396 4746.28206 R-squared = 0.7672
-------------+------------------------------ Adj R-squared = 0.7654
Total | 8073672.00 399 20234.7669 Root MSE = 68.893
------------------------------------------------------------------------------
api00 Coef. Std. Err. t P>|t| [95% Conf. Interval]
------------------------------------------------------------------------------
_cons 483.3699 7.45694 64.82 0.000 468.7098 498.03
yr_rnd
1 42.96006 9.361761 4.59 0.000 24.55509 61.36502
2 (dropped)
mealcat
1 281.6832 9.445676 29.82 0.000 263.1132 300.2531
2 117.9458 9.188911 12.84 0.000 99.88066 136.011
3 (dropped)
------------------------------------------------------------------------------
anova will display the parameter estimates from the last anova model. However, the anova command is rigid in its determination of which group will be the omitted group and the last group is dropped. Since this differs from the coding we used in the regression commands above, the parameter estimates from this anova command will differ from the regress command above.
In summary, these results indicate the differences between year round and non-year round schools is significant, and the differences among the three mealcat groups are significant.
3.5 Categorical predictor with interactions
3.5.1 using xi
Let’s perform the same analysis that we performed above, this time let’s include the interaction of mealcat by yr_rnd. When using xi, it is easy to include an interaction term, as shown below.
xi : regress api00 i.mealcat*yr_rnd
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_3 omitted)
i.meal~t*yr_rnd _ImeaXyr_rn_# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 261.61
Model | 6204727.82 5 1240945.56 Prob > F = 0.0000
Residual | 1868944.18 394 4743.51314 R-squared = 0.7685
-------------+------------------------------ Adj R-squared = 0.7656
Total | 8073672.00 399 20234.7669 Root MSE = 68.873
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 288.1929 10.44284 27.60 0.000 267.6623 308.7236
_Imealcat_2 | 123.781 10.55185 11.73 0.000 103.036 144.5259
yr_rnd | -33.49254 11.77129 -2.85 0.005 -56.63492 -10.35015
_ImeaXyr_r~1 | -40.76438 29.23118 -1.39 0.164 -98.23297 16.70422
_ImeaXyr_r~2 | -18.24763 22.25624 -0.82 0.413 -62.00347 25.5082
_cons | 521.4925 8.414197 61.98 0.000 504.9502 538.0349
------------------------------------------------------------------------------
We can test the overall interaction with the test command. This interaction effect is not significant.
test _ImeaXyr_rn_1 _ImeaXyr_rn_2
( 1) _ImeaXyr_rn_1 = 0.0
( 2) _ImeaXyr_rn_2 = 0.0
F( 2, 394) = 1.12
Prob > F = 0.3288
It is important to note how the meaning of the coefficients change in the presence of these interaction terms. For example, in the prior model, with only main effects, we could interpret Byr_rnd as the difference between the year round and non year round schools. However, now that we have added the interaction term, the term Byr_rnd represents the difference between cell3 and cell6, or the difference between the year round and non-year round schools when mealcat=3 (because mealcat=3 was the omitted group). The presence of an interaction would imply that the difference between year round and non-year round schools depends on the level of mealcat. The interaction terms B_ImeaXyr_rn_1 and B_ImeaXyr_rn_2 represent the extent to which the difference between the year round/non year round schools changes when mealcat=1 and when mealcat=2 (as compared to the reference group, mealcat=3). For example the term B_ImeaXyr_rn_1 represents the difference between year round and non-year round for mealcat=1 vs. the difference for mealcat=3. In other words, B_ImeaXyr_rn_1 in this design is (cell1-cell4) – (cell3-cell6), or it represents how much the effect of yr_rnd differs between mealcat=1 and mealcat=3.
Below we have shown the predicted values for the six cells in terms of the coefficients in the model. If you compare this to the main effects model, you will see that the predicted values are the same except for the addition of _ImeaXyr_rn_1 (in cell 4) and _ImeaXyr_rn_2 (in cell 5).
mealcat=1 mealcat=2 mealcat=3
-------------------------------------------------
yr_rnd=0 _cons _cons _cons
+BImealcat1 +BImealcat2
-------------------------------------------------
yr_rnd=1 _cons _cons _cons
+Byr_rnd +Byr_rnd +Byr_rnd
+BImealcat1 +BImealcat2
+B_ImeaXyr_rn_1 +B_ImeaXyr_rn_2
It can be very tricky to interpret these interaction terms if you wish to form specific comparisons. For example, if you wanted to perform a test of the simple main effect of yr_rnd when mealcat=1, i.e., comparing cell1 with cell4, you would want to compare _cons+ BImealcat1 vs. _cons + B yr_rnd + BImealcat1+ BImeaXyr_rn_1 and since _cons and Imealcat1 would drop out, we would test
test _b[yr_rnd] +_b[_ImeaXyr_rn_1] ==0
( 1) yr_rnd + _ImeaXyr_rn_1 = 0.0
F( 1, 394) = 7.70
Prob > F = 0.0058
This test is significant, indicating that the effect of yr_rnd is significant for the mealcat = 1 group.
As we will see, such tests can be more easily done via anova.
3.5.2 Using anova
Constructing these interactions can be somewhat easier when using the anova command. As you see below, the anova command gives us the test of the overall main effects and interactions without the need to perform subsequent test commands.
anova api00 yr_rnd mealcat yr_rnd*mealcat
Number of obs = 400 R-squared = 0.7685
Root MSE = 68.8732 Adj R-squared = 0.7656
Source | Partial SS df MS F Prob > F
---------------+----------------------------------------------------
Model | 6204727.82 5 1240945.56 261.61 0.0000
|
yr_rnd | 99617.3706 1 99617.3706 21.00 0.0000
mealcat | 1796232.80 2 898116.399 189.34 0.0000
yr_rnd*mealcat | 10583.5187 2 5291.75936 1.12 0.3288
|
Residual | 1868944.18 394 4743.51314
---------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
It is easy to perform tests of simple main effects using the sme command. You can download sme from within Stata by typing search sme (see How can I used the search command to search for programs and get additional help? for more information about using search).
Now we can test the simple main effects of yr_rnd at each level of mealcat.
sme yr_rnd mealcat Test of yr_rnd at mealcat(1): F(1/394) = 7.7023296 Test of yr_rnd at mealcat(2): F(1/394) = 7.5034121 Test of yr_rnd at mealcat(3): F(1/394) = 8.0955856 Critical value of F for alpha = .05 using ... -------------------------------------------------- Dunn's procedure = 4.7435944 Marascuilo & Levin = 5.4561926 per family error rate = 5.7804 simultaneous test procedure = 8.1680324
The results from sme show us the effect of yr_rnd at each of the 3 levels of mealcat. We can see that the comparison for mealcat = 1 matches those we computed above using the test statement, however, it was much easier and less error prone using the sme command.
Although this section has focused on how to handle analyses involving interactions, these particular results show no indication of interaction. We could decide to omit interaction terms from future analyses having found the interactions to be non-significant. This would simplify future analyses, however including the interaction term can be useful to assure readers that the interaction term is non-significant.
3.6 Continuous and Categorical variables
3.6.1 Using regress
Say that we wish to analyze both continuous and categorical variables in one analysis. For example, let’s include yr_rnd and some_col in the same analysis.
regress api00 yr_rnd some_col
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 2, 397) = 68.54
Model | 2072201.84 2 1036100.92 Prob > F = 0.0000
Residual | 6001470.16 397 15117.0533 R-squared = 0.2567
-------------+------------------------------ Adj R-squared = 0.2529
Total | 8073672.00 399 20234.7669 Root MSE = 122.95
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -149.1591 14.87519 -10.03 0.000 -178.4031 -119.9151
some_col | 2.235689 .5528656 4.04 0.000 1.148779 3.322599
_cons | 637.8581 13.50332 47.24 0.000 611.3111 664.405
------------------------------------------------------------------------------
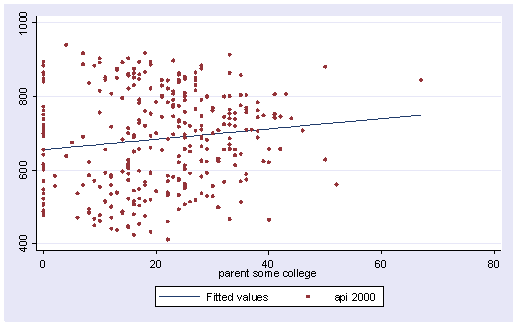
We can create the predicted values using the predict command.
predict yhat (option xb assumed; fitted values)
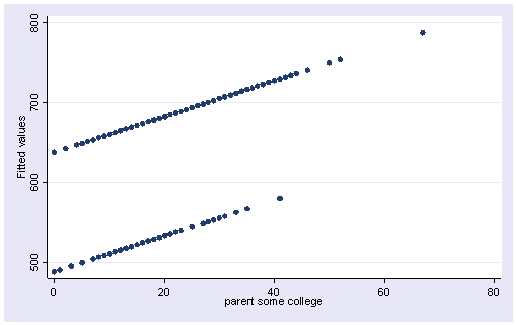
Let’s graph the predicted values by some_col.
scatter yhat some_col
The coefficient for some_col indicates that for every unit increase in some_col the api00 score is predicted to increase by 2.23 units. This is the slope of the lines shown in the above graph. The graph has two lines, one for the year round schools and one for the non-year round schools. The coefficient for yr_rnd is -149.16, indicating that as yr_rnd increases by 1 unit, the api00 score is expected to decrease by about 149 units. As you can see in the graph, the top line is about 150 units higher than the lower line. You can see that the intercept is 637 and that is where the upper line crosses the Y axis when X is 0. The lower line crosses the line about 150 units lower at about 487.
3.6.2 Using anova
We can run this analysis using the anova command. The anova command assumes that the variables are categorical, thus, we need to use the continuous() option (which can be abbreviated as cont()) to specify that some_col is a continuous variable.
anova api00 yr_rnd some_col, cont(some_col)
Number of obs = 400 R-squared = 0.2567
Root MSE = 122.951 Adj R-squared = 0.2529
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 2072201.84 2 1036100.92 68.54 0.0000
|
yr_rnd | 1519992.67 1 1519992.67 100.55 0.0000
some_col | 247201.276 1 247201.276 16.35 0.0001
|
Residual | 6001470.16 397 15117.0533
-----------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
If we square the t-values from the regress command (above), we would find that they match those of the anova command.
3.7 Interactions of Continuous by 0/1 Categorical variables
Above we showed an analysis that looked at the relationship between some_col and api00 and also included yr_rnd. We saw that this produced a graph where we saw the relationship between some_col and api00 but there were two regression lines, one higher than the other but with equal slope. Such a model assumed that the slope was the same for the two groups. Perhaps the slope might be different for these groups. Let’s run the regressions separately for these two groups beginning with the non-year round schools.
regress api00 some_col if yr_rnd==0
Source | SS df MS Number of obs = 308
-------------+------------------------------ F( 1, 306) = 4.91
Model | 84700.8576 1 84700.8576 Prob > F = 0.0274
Residual | 5273591.67 306 17233.9597 R-squared = 0.0158
-------------+------------------------------ Adj R-squared = 0.0126
Total | 5358292.53 307 17453.7216 Root MSE = 131.28
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 1.409427 .6357572 2.22 0.027 .1584181 2.660436
_cons | 655.1103 15.23704 42.99 0.000 625.1277 685.0929
------------------------------------------------------------------------------
predict yhat0 if yr_rnd==0
(option xb assumed; fitted values)
(92 missing values generated)
scatter yhat0 api00 some_col if yr_rnd==0, connect(l i) msymbol(i o) sort
Likewise, let’s look at the year round schools.
regress api00 some_col if yr_rnd==1
Source | SS df MS Number of obs = 92
-------------+------------------------------ F( 1, 90) = 65.08
Model | 373644.064 1 373644.064 Prob > F = 0.0000
Residual | 516734.838 90 5741.4982 R-squared = 0.4196
-------------+------------------------------ Adj R-squared = 0.4132
Total | 890378.902 91 9784.38354 Root MSE = 75.773
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 7.402618 .9176327 8.07 0.000 5.57958 9.225655
_cons | 407.0391 16.51462 24.65 0.000 374.2299 439.8482
------------------------------------------------------------------------------
predict yhat1 if yr_rnd==1
(option xb assumed; fitted values)
(308 missing values generated)
scatter yhat1 api00 some_col if yr_rnd==1, connect(l i) msymbol(i o) sort
Note that the slope of the regression line looks much steeper for the year round schools than for the non-year round schools. This is confirmed by the regression equations that show the slope for the year round schools to be higher (7.4) than non-year round schools (1.3). We can compare these to see if these are significantly different from each other by including the interaction of some_col by yr_rnd, an interaction of a continuous variable by a categorical variable.
3.7.1 Computing interactions manually
We will start by manually computing the interaction of some_col by yr_rnd. Let’s start fresh and use the elemapi2 data file using the , clear option to clear out any variables we have previously created.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
Next, let’s make a variable that is the interaction of some college (some_col) and year round schools (yr_rnd) called yrXsome.
gen yrXsome = yr_rnd*some_col
We can now run the regression that tests whether the coefficient for some_col is significantly different for year round schools and non-year round schools. Indeed, the yrXsome interaction effect is significant.
regress api00 some_col yr_rnd yrXsome
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 52.05
Model | 2283345.48 3 761115.162 Prob > F = 0.0000
Residual | 5790326.51 396 14622.0366 R-squared = 0.2828
-------------+------------------------------ Adj R-squared = 0.2774
Total | 8073672.00 399 20234.7669 Root MSE = 120.92
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 1.409427 .5856022 2.41 0.017 .2581494 2.560705
yr_rnd | -248.0712 29.85895 -8.31 0.000 -306.7731 -189.3694
yrXsome | 5.99319 1.57715 3.80 0.000 2.892557 9.093824
_cons | 655.1103 14.03499 46.68 0.000 627.5179 682.7027
------------------------------------------------------------------------------
We can make a graph showing the regression lines for the two types of schools showing how different their regression lines are. We first create the predicted value, we call it yhata.
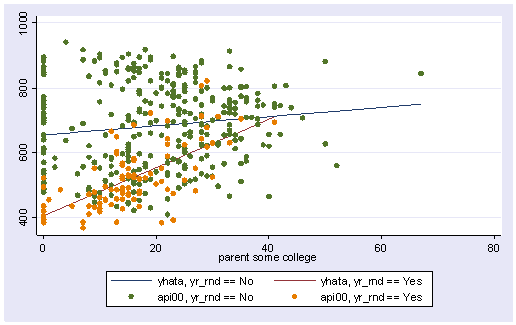
predict yhata (option xb assumed; fitted values)
Then, we create separate variables for the two types of schools which will be called yhata0 for non-year round schools and yhata1 for year round schools.
separate yhata, by(yr_rnd)
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
yhata0 float %9.0g yhata, yr_rnd == 0
yhata1 float %9.0g yhata, yr_rnd == 1
We can then graph the predicted values for the two types of schools by some_col. You can see how the two lines have quite different slopes, consistent with the fact that the yrXsome interaction was significant. The c(ll[_]) option indicates that yhata0 should be connected with a line, and yhata1 should be connected with dashed lines (because we included [_] after the l ). If we had used l[.] it would have made a dotted line. The options to make dashed and dotted lines are new to Stata 7 and you can find more information via help grsym .
line yhata0 yhata1 some_col, sort
We can replot the same graph including the data points.
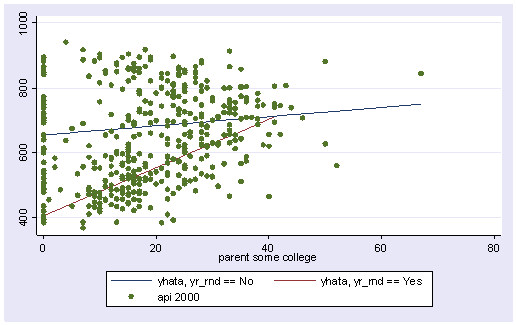
twoway (line yhata0 yhata1 some_col, sort) (scatter api00 some_col)
The graph above used the same kind of dots for the data points for both types of schools. Let’s make separate variables for the api00 scores for the two types of schools called api000 for the non-year round schools and api001 for the year round schools.
separate api00, by(yr_rnd)
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
api000 int %6.0g api00, yr_rnd == 0
api001 int %6.0g api00, yr_rnd == 1
We can then make the same graph as above except show the points differently for the two types of schools. Below we use small circles for the non-year round schools, and triangles for the year round schools.
twoway (line yhata0 yhata1 some_col, sort) (scatter api000 api001 some_col)
Let’s quickly run the regressions again where we performed separate regressions for the two groups
Non-year round
regress api00 some_col if yr_rnd==0
Source | SS df MS Number of obs = 308
-------------+------------------------------ F( 1, 306) = 4.91
Model | 84700.8576 1 84700.8576 Prob > F = 0.0274
Residual | 5273591.67 306 17233.9597 R-squared = 0.0158
-------------+------------------------------ Adj R-squared = 0.0126
Total | 5358292.53 307 17453.7216 Root MSE = 131.28
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 1.409427 .6357572 2.22 0.027 .1584181 2.660436
_cons | 655.1103 15.23704 42.99 0.000 625.1277 685.0929
------------------------------------------------------------------------------
Year round
regress api00 some_col if yr_rnd==1
Source | SS df MS Number of obs = 92
-------------+------------------------------ F( 1, 90) = 65.08
Model | 373644.064 1 373644.064 Prob > F = 0.0000
Residual | 516734.838 90 5741.4982 R-squared = 0.4196
-------------+------------------------------ Adj R-squared = 0.4132
Total | 890378.902 91 9784.38354 Root MSE = 75.773
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 7.402618 .9176327 8.07 0.000 5.57958 9.225655
_cons | 407.0391 16.51462 24.65 0.000 374.2299 439.8482
------------------------------------------------------------------------------
Now, let’s show the regression for both types of schools with the interaction term.
regress api00 some_col yr_rnd yrXsome
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 52.05
Model | 2283345.48 3 761115.162 Prob > F = 0.0000
Residual | 5790326.51 396 14622.0366 R-squared = 0.2828
-------------+------------------------------ Adj R-squared = 0.2774
Total | 8073672.00 399 20234.7669 Root MSE = 120.92
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
some_col | 1.409427 .5856022 2.41 0.017 .2581494 2.560705
yr_rnd | -248.0712 29.85895 -8.31 0.000 -306.7731 -189.3694
yrXsome | 5.99319 1.57715 3.80 0.000 2.892557 9.093824
_cons | 655.1103 14.03499 46.68 0.000 627.5179 682.7027
------------------------------------------------------------------------------
Note that the coefficient for some_col in the combined analysis is the same as the coefficient for some_col for the non-year round schools? This is because non-year round schools are the reference group. Then, the coefficient for the yrXsome interaction in the combined analysis is the Bsome_col for the year round schools (7.4) minus Bsome_col for the non year round schools (1.41) yielding 5.99. This interaction is the difference in the slopes of some_col for the two types of schools, and this is why this is useful for testing whether the regression lines for the two types of schools are equal. If the two types of schools had the same regression coefficient for some_col, then the coefficient for the yrXsome interaction would be 0. In this case, the difference is significant, indicating that the regression lines are significantly different.
So, if we look at the graph of the two regression lines we can see the difference in the slopes of the regression lines (see graph below). Indeed, we can see that the non-year round schools (the solid line) have a smaller slope (1.4) than the slope for the year round schools (7.4). The difference between these slopes is 5.99, the coefficient for yrXsome.
line yhata0 yhata1 some_col, sort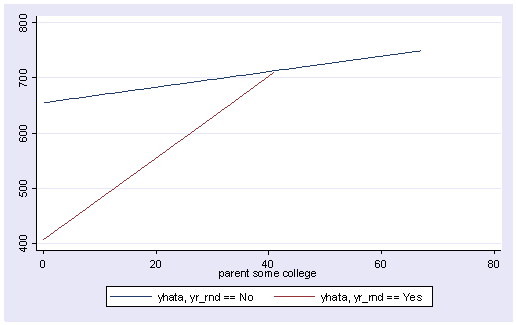
3.7.2 Computing interactions with xi
We can use the xi command for doing this kind of analysis as well. Let’s start fresh and use the elemapi2 file.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2, clear
We can run a model just like the model we showed above using the xi command. You can compare the results to those above and see that we get the exact same results.
xi : regress api00 i.yr_rnd*some_col
i.yr_rnd _Iyr_rnd_1-2 (naturally coded; _Iyr_rnd_1 omitted)
i.yr_rnd*some~l _Iyr_Xsome__# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 3, 396) = 52.05
Model | 2283345.48 3 761115.162 Prob > F = 0.0000
Residual | 5790326.51 396 14622.0366 R-squared = 0.2828
-------------+------------------------------ Adj R-squared = 0.2774
Total | 8073672.00 399 20234.7669 Root MSE = 120.92
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iyr_rnd_2 | -248.0712 29.85895 -8.31 0.000 -306.7731 -189.3694
some_col | 1.409427 .5856022 2.41 0.017 .2581494 2.560705
_Iyr_Xsome~2 | 5.99319 1.57715 3.80 0.000 2.892557 9.093824
_cons | 655.1103 14.03499 46.68 0.000 627.5179 682.7027
------------------------------------------------------------------------------
The i.yr_rnd*some_col term creates 3 terms, some_col, _Iyr_rnd_2 an indicator variable for yr_rnd representing whether the school is year round and the variable _Iyr_Xsome~2 representing the interaction of yr_rnd by some_col.
As we did above, we can create predicted values and create graphs showing the regression lines for the two types of schools. We omit showing these commands.
3.7.3 Computing interactions with anova
We can also run a model just like the model we showed above using the anova command. We include the terms yr_rnd some_col and the interaction yr_rnr*some_col
anova api00 yr_rnd some_col yr_rnd*some_col, contin(some_col)
Number of obs = 400 R-squared = 0.2828
Root MSE = 120.922 Adj R-squared = 0.2774
Source | Partial SS df MS F Prob > F
----------------+----------------------------------------------------
Model | 2283345.48 3 761115.162 52.05 0.0000
|
yr_rnd | 1009279.99 1 1009279.99 69.02 0.0000
some_col | 456473.187 1 456473.187 31.22 0.0000
yr_rnd*some_col | 211143.646 1 211143.646 14.44 0.0002
|
Residual | 5790326.51 396 14622.0366
----------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
As we illustrated above, we can compute the predicted values using the predict command and graph the separate regression lines. These commands are omitted.
In this section we found that the relationship between some_col and api00 depended on whether the school is a year round school or a non-year round school. For the year round schools, the relationship between some_col and api00 was significantly stronger than for non-year round schools. In general, this type of analysis allows you to test whether the strength of the relationship between two continuous variables varies based on the categorical variable.
3.8 Continuous and Categorical variables, interaction with 1/2/3 variable The prior examples showed how to do regressions with a continuous variable and a categorical variable that has 2 levels. These examples will extend this further by using a categorical variable with 3 levels, mealcat.
3.8.1 using xi
We can use the xi command to run a model with some_col, mealcat and the interaction of these two variables.
xi : regress api00 i.mealcat*some_col
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_1 omitted)
i.meal~t*some~l _ImeaXsome__# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 263.00
Model | 6212306.88 5 1242461.38 Prob > F = 0.0000
Residual | 1861365.12 394 4724.27696 R-squared = 0.7695
-------------+------------------------------ Adj R-squared = 0.7665
Total | 8073672.00 399 20234.7669 Root MSE = 68.733
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_2 | -239.03 18.66502 -12.81 0.000 -275.7255 -202.3345
_Imealcat_3 | -344.9476 17.05743 -20.22 0.000 -378.4825 -311.4126
some_col | -.9473385 .4873679 -1.94 0.053 -1.905505 .0108284
_ImeaXsome~2 | 3.140945 .7292897 4.31 0.000 1.707159 4.57473
_ImeaXsome~3 | 2.607308 .8960435 2.91 0.004 .8456841 4.368933
_cons | 825.8937 11.99182 68.87 0.000 802.3177 849.4697
------------------------------------------------------------------------------
The interaction now has two terms (_ImeaXsome~2 and _ImeaXsome~3). To get an overall test of this interaction, we can use the test command.
test _ImeaXsome__2 _ImeaXsome__3
( 1) _ImeaXsome__2 = 0.0
( 2) _ImeaXsome__3 = 0.0
F( 2, 394) = 10.32
Prob > F = 0.0000
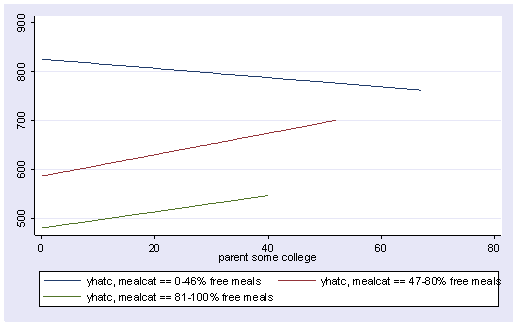
These results indicate that the overall interaction is indeed significant. This means that the regression lines from the 3 groups differ significantly. As we have done before, let’s compute the predicted values and make a graph of the predicted values so we can see how the regression lines differ.
predict yhatc
(option xb assumed; fitted values)
separate yhatc, by(mealcat)
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
yhatc1 float %9.0g yhatc, mealcat == 1
yhatc2 float %9.0g yhatc, mealcat == 2
yhatc3 float %9.0g yhatc, mealcat == 3
Since we had three groups, we get three regression lines, one for each category of mealcat. The solid line is for group 1, the dashed line for group 2, and the dotted line is for group 3.
line yhatc1 yhatc2 yhatc3 some_col, sort
Group 1 was the omitted group, therefore the slope of the line for group 1 is the coefficient for some_col which is -.94. Indeed, this line has a downward slope. If we add the coefficient for some_col to the coefficient for _ImeaXsome~2 we get the coefficient for group 2, i.e., 3.14 + -.94 yields 2.2, the slope for group 2. Indeed, group 2 shows an upward slope. Likewise, if we add the coefficient for some_col to the coefficient for _ImeaXsome~3 we get the coefficient for group 3, i.e., 2.6 + -.94 yields 1.66, the slope for group 3,. So, the slopes for the 3 groups are
group 1: -0.94 group 2: 2.2 group 3: 1.66
The test of the coefficient for _ImeaXsome~2 tested whether the coefficient for group 2 differed from group 1, and indeed this was significant. Likewise, the test of the coefficient for _ImeaXsome~3 tested whether the coefficient for group 3 differed from group 1, and indeed this was significant. What did the test of the coefficient some_col test? This coefficient represents the coefficient for group 1, so this tested whether the coefficient for group 1 (-0.94) was significantly different from 0. This is probably a non-interesting test.
The comparisons in the above analyses don’t seem to be as interesting as comparing group 1 vs. 2 and then comparing group 2 vs. 3. These successive comparisons seem much more interesting. We can do this by making group 2 the omitted group, and then each group would be compared to group 2. As we have done before, we will use the char command to indicate that we want group 2 to be the omitted category and then rerun the regression.
char mealcat[omit] 2
xi : regress api00 i.mealcat*some_col
i.mealcat _Imealcat_1-3 (naturally coded; _Imealcat_2 omitted)
i.meal~t*some~l _ImeaXsome__# (coded as above)
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 263.00
Model | 6212306.88 5 1242461.38 Prob > F = 0.0000
Residual | 1861365.12 394 4724.27696 R-squared = 0.7695
-------------+------------------------------ Adj R-squared = 0.7665
Total | 8073672.00 399 20234.7669 Root MSE = 68.733
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Imealcat_1 | 239.03 18.66502 12.81 0.000 202.3345 275.7255
_Imealcat_3 | -105.9176 18.7545 -5.65 0.000 -142.789 -69.0462
some_col | 2.193606 .5425274 4.04 0.000 1.126996 3.260217
_ImeaXsome~1 | -3.140945 .7292897 -4.31 0.000 -4.57473 -1.707159
_ImeaXsome~3 | -.5336362 .9272014 -0.58 0.565 -2.356517 1.289245
_cons | 586.8637 14.30311 41.03 0.000 558.7438 614.9837
------------------------------------------------------------------------------
Now, the test of _ImeaXsome~1 tests whether the coefficient for group 1 differs from group 2, and it does. Then, the test of _ImeaXsome~3 tests whether the coefficient for group 3 significantly differs from group 2, and it does not. This makes sense given the graph and given the estimates of the coefficients that we have, that -.94 is significantly different from 2.2 but 2.2 is not significantly different from 1.66.
3.8.2 Using Anova
We can perform the same analysis using the anova command, as shown below. The anova command gives us somewhat less flexibility since we cannot choose which group is the omitted group.
use elemapi2, clear
anova api00 mealcat some_col mealcat*some_col, cont(some_col)
Number of obs = 400 R-squared = 0.7695
Root MSE = 68.7334 Adj R-squared = 0.7665
Source | Partial SS df MS F Prob > F
-----------------+----------------------------------------------------
Model | 6212306.88 5 1242461.38 263.00 0.0000
|
mealcat | 2012065.49 2 1006032.75 212.95 0.0000
some_col | 36366.3662 1 36366.3662 7.70 0.0058
mealcat*some_col | 97468.1685 2 48734.0843 10.32 0.0000
|
Residual | 1861365.12 394 4724.27696
-----------------+----------------------------------------------------
Total | 8073672.00 399 20234.7669
Because the anova command omits the 3rd category, and the analysis we showed above omitted the second category, the parameter estimates will not be the same. You can compare the results from below with the results above and see that the parameter estimates are not the same. Because group 3 is dropped, that is the reference category and all comparisons are made with group 3.
anova, regress
Source | SS df MS Number of obs = 400
-------------+------------------------------ F( 5, 394) = 263.00
Model | 6212306.88 5 1242461.38 Prob > F = 0.0000
Residual | 1861365.12 394 4724.27696 R-squared = 0.7695
-------------+------------------------------ Adj R-squared = 0.7665
Total | 8073672.00 399 20234.7669 Root MSE = 68.733
------------------------------------------------------------------------------
api00 Coef. Std. Err. t P>|t| [95% Conf. Interval]
------------------------------------------------------------------------------
_cons 480.9461 12.13063 39.65 0.000 457.0973 504.795
meals3
1 344.9476 17.05743 20.22 0.000 311.4126 378.4825
2 105.9176 18.7545 5.65 0.000 69.0462 142.789
3 (dropped)
some_col 1.65997 .7519086 2.21 0.028 .1817153 3.138225
meals3*some_col
1 -2.607308 .8960435 -2.91 0.004 -4.368933 -.8456841
2 .5336362 .9272014 0.58 0.565 -1.289245 2.356517
3 (dropped)
------------------------------------------------------------------------------
These analyses showed that the relationship between some_col and api00 varied, depending on the level of mealcat. In comparing group 1 with group 2, the coefficient for some_col was significantly different, but there was no difference in the coefficient for some_col in comparing groups 2 and 3.
3.9 Summary
This covered four techniques for analyzing data with categorical variables, 1) manually constructing indicator variables, 2) creating indicator variables using the xi command, 3) coding variables using xi3, and 4) using the anova command. Each method has its advantages and disadvantages, as described below.
Manually constructing indicator variables can be very tedious and even error prone. For very simple models, it is not very difficult to create your own indicator variables, but if you have categorical variables with many levels and/or interactions of categorical variables, it can be laborious to manually create indicator variables. However, the advantage is that you can have quite a bit of control over how the variables are created and the terms that are entered into the model.
The xi command can really ease the creation of indicator variables, and make it easier to include interactions in your models by allowing you to include interaction terms such as i.prog*female . The xi command also gives you the flexibility to decide which category would be the omitted category (unlike the anova command).
The anova command eliminates the need to create indicator variables making it easy to include variables that have lots of categories, and making it easy to create interactions by allowing you to include terms like some_col*mealcat. It can be easier to perform tests of simple main effects with the anova command. However, the anova command is not flexible in letting you choose which category is the omitted category (the last category is always the omitted category).
As you will see in the next chapter, the regress command includes additional options like the robust option and the cluster option that allow you to perform analyses when you don’t exactly meet the assumptions of ordinary least squares regression. In such cases, the regress command offers features not available in the anova command and may be more advantageous to use.
3.10 Self Assessment
1. Using the elemapi2 data file ( use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) convert the variable ell into 2 categories using the following coding, 0-25 on ell becomes 0, and 26-100 on ell becomes 1. Use this recoded version of ell to predict api00 and interpret the results.
2. Convert the variable ell into 3 categories coding those scoring 0-14 on ell as 1, and those 15/41 as 2 and 42/100 as 3. Do an analysis predicting api00 from the ell variable converted to a 1/2/3 variable. Interpret the results.
3. Do a regression analysis predicting api00 from yr_rnd and the ell variable converted to a 0/1 variable. Then create an interaction term and run the analysis again. Interpret the results of these analyses.
4. Do a regression analysis predicting api00 from ell coded as 0/1 (from question 1) and some_col, and the interaction of these two variables. Interpret the results, including showing a graph of the results.
5. Use the variable ell converted into 3 categories (from question 2) and predict api00 from ell in 3 categories, from some_col and the interaction. of these two variables. Interpret the results, including showing a graph.
Click here for our answers to these self assessment questions.
3.11 For more information
- Stata Manuals
- [R] xi
- [R] anova
- [R] test
- Web Links
- Creating Dummy Variables – Stata FAQ- How can I create dummy variables in Stata
- Models with interactions of continuous and categorical variables – Stata FAQ- How can I compare regression coefficients between 2 groups – Stata FAQ- How can I compare regression coefficients across 3 (or more) groups
- Other- Stata FAQ: How can I form various tests comparing the different levels of a categorical variable after anova or regress? – Stata FAQ- Why do estimation commands sometimes drop variables (from Stata FAQs)