Chapter Outline
4.1 Robust Regression Methods 4.1.1 Regression with Robust Standard Errors 4.1.2 Using the Cluster Option 4.1.3 Robust Regression 4.1.4 Quantile Regression 4.2 Constrained Linear Regression 4.3 Regression with Censored or Truncated Data 4.3.1 Regression with Censored Data 4.3.2 Regression with Truncated Data 4.4 Regression with Measurement Error 4.5 Multiple Equation Regression Models 4.5.1 Seemingly Unrelated Regression 4.5.2 Multivariate Regression 4.6 Summary 4.7 Self assessment 4.8 For more information
In this chapter we will go into various commands that go beyond OLS. This chapter is a bit different from the others in that it covers a number of different concepts, some of which may be new to you. These extensions, beyond OLS, have much of the look and feel of OLS but will provide you with additional tools to work with linear models.
The topics will include robust regression methods, constrained linear regression, regression with censored and truncated data, regression with measurement error, and multiple equation models.
4.1 Robust Regression Methods
It seems to be a rare dataset that meets all of the assumptions underlying multiple regression. We know that failure to meet assumptions can lead to biased estimates of coefficients and especially biased estimates of the standard errors. This fact explains a lot of the activity in the development of robust regression methods.
The idea behind robust regression methods is to make adjustments in the estimates that take into account some of the flaws in the data itself. We are going to look at three approaches to robust regression: 1) regression with robust standard errors including the cluster option, 2) robust regression using iteratively reweighted least squares, and 3) quantile regression, more specifically, median regression.
Before we look at these approaches, let’s look at a standard OLS regression using the elementary school academic performance index (elemapi2.dta) dataset.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2
We will look at a model that predicts the api 2000 scores using the average class size in K through 3 (acs_k3), average class size 4 through 6 (acs_46), the percent of fully credentialed teachers (full), and the size of the school (enroll). First let’s look at the descriptive statistics for these variables. Note the missing values for acs_k3 and acs_k6.
summarize api00 acs_k3 acs_46 full enroll
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
api00 | 400 647.6225 142.249 369 940
acs_k3 | 398 19.1608 1.368693 14 25
acs_46 | 397 29.68514 3.840784 20 50
full | 400 84.55 14.94979 37 100
enroll | 400 483.465 226.4484 130 1570
Below we see the regression predicting api00 from acs_k3, acs_46 full and enroll. We see that all of the variables are significant except for acs_k3.
regress api00 acs_k3 acs_46 full enroll
Source | SS df MS Number of obs = 395
---------+------------------------------ F( 4, 390) = 61.01
Model | 3071909.06 4 767977.265 Prob > F = 0.0000
Residual | 4909500.73 390 12588.4634 R-squared = 0.3849
---------+------------------------------ Adj R-squared = 0.3786
Total | 7981409.79 394 20257.3852 Root MSE = 112.20
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
acs_k3 | 6.954381 4.371097 1.591 0.112 -1.63948 15.54824
acs_46 | 5.966015 1.531049 3.897 0.000 2.955873 8.976157
full | 4.668221 .4142537 11.269 0.000 3.853771 5.482671
enroll | -.1059909 .0269539 -3.932 0.000 -.1589841 -.0529977
_cons | -5.200407 84.95492 -0.061 0.951 -172.2273 161.8265
------------------------------------------------------------------------------
We can use the test command to test both of the class size variables, and we find the overall test of these two variables is significant.
test acs_k3 acs_46
( 1) acs_k3 = 0.0
( 2) acs_46 = 0.0
F( 2, 390) = 11.08
Prob > F = 0.0000
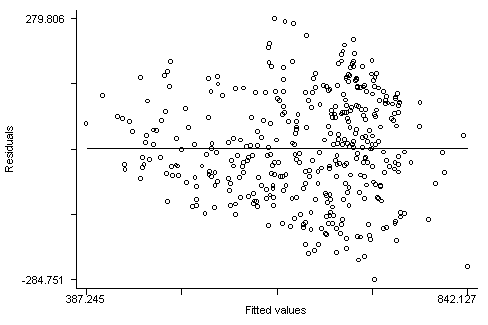
Here is the residual versus fitted plot for this regression. Notice that the pattern of the residuals is not exactly as we would hope. The spread of the residuals is somewhat wider toward the middle right of the graph than at the left, where the variability of the residuals is somewhat smaller, suggesting some heteroscedasticity.
rvfplot
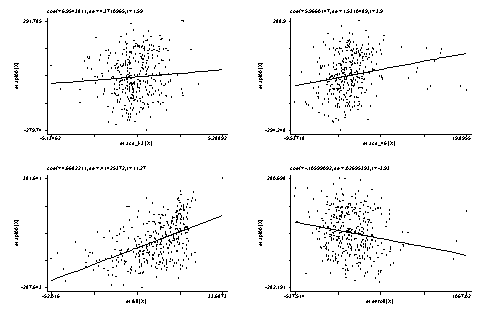
Below we show the avplots. Although the plots are small, you can see some points that are of concern. There is not a single extreme point (like we saw in chapter 2) but a handful of points that stick out. For example, in the top right graph you can see a handful of points that stick out from the rest. If this were just one or two points, we might look for mistakes or for outliers, but we would be more reluctant to consider such a large number of points as outliers.
avplots
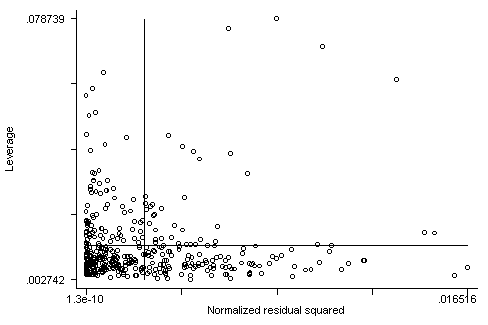
Here is the lvr2plot for this regression. We see 4 points that are somewhat high in both their leverage and their residuals.
lvr2plot
None of these results are dramatic problems, but the rvfplot suggests that there might be some outliers and some possible heteroscedasticity; the avplots have some observations that look to have high leverage, and the lvr2plot shows some points in the upper right quadrant that could be influential. We might wish to use something other than OLS regression to estimate this model. In the next several sections we will look at some robust regression methods.
4.1.1 Regression with Robust Standard Errors
The Stata regress command includes a robust option for estimating the standard errors using the Huber-White sandwich estimators. Such robust standard errors can deal with a collection of minor concerns about failure to meet assumptions, such as minor problems about normality, heteroscedasticity, or some observations that exhibit large residuals, leverage or influence. For such minor problems, the robust option may effectively deal with these concerns.
With the robust option, the point estimates of the coefficients are exactly the same as in ordinary OLS, but the standard errors take into account issues concerning heterogeneity and lack of normality. Here is the same regression as above using the robust option. Note the changes in the standard errors and t-tests (but no change in the coefficients). In this particular example, using robust standard errors did not change any of the conclusions from the original OLS regression.
regress api00 acs_k3 acs_46 full enroll, robust
Regression with robust standard errors Number of obs = 395
F( 4, 390) = 84.67
Prob > F = 0.0000
R-squared = 0.3849
Root MSE = 112.20
------------------------------------------------------------------------------
| Robust
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
acs_k3 | 6.954381 4.620599 1.505 0.133 -2.130019 16.03878
acs_46 | 5.966015 1.573214 3.792 0.000 2.872973 9.059057
full | 4.668221 .4146813 11.257 0.000 3.852931 5.483512
enroll | -.1059909 .0280154 -3.783 0.000 -.1610711 -.0509108
_cons | -5.200407 86.66308 -0.060 0.952 -175.5857 165.1849
------------------------------------------------------------------------------
4.1.2 Using the Cluster Option
As described in Chapter 2, OLS regression assumes that the residuals are independent. The elemapi2 dataset contains data on 400 schools that come from 37 school districts. It is very possible that the scores within each school district may not be independent, and this could lead to residuals that are not independent within districts. We can use the cluster option to indicate that the observations are clustered into districts (based on dnum) and that the observations may be correlated within districts, but would be independent between districts.
By the way, if we did not know the number of districts, we could quickly find out how many districts there are as shown below, by quietly tabulating dnum and then displaying the macro r(r) which gives the numbers of rows in the table, which is the number of school districts in our data.
quietly tabulate dnum display r(r) 37
Now, we can run regress with the cluster option. We do not need to include the robust option since robust is implied with cluster. Note that the standard errors have changed substantially, much more so, than the change caused by the robust option by itself.
regress api00 acs_k3 acs_46 full enroll, cluster(dnum)
Regression with robust standard errors Number of obs = 395
F( 4, 36) = 31.18
Prob > F = 0.0000
R-squared = 0.3849
Number of clusters (dnum) = 37 Root MSE = 112.20
------------------------------------------------------------------------------
| Robust
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
acs_k3 | 6.954381 6.901117 1.008 0.320 -7.041734 20.9505
acs_46 | 5.966015 2.531075 2.357 0.024 .8327565 11.09927
full | 4.668221 .7034641 6.636 0.000 3.24153 6.094913
enroll | -.1059909 .0429478 -2.468 0.018 -.1930931 -.0188888
_cons | -5.200407 121.7856 -0.043 0.966 -252.193 241.7922
------------------------------------------------------------------------------
As with the robust option, the estimate of the coefficients are the same as the OLS estimates, but the standard errors take into account that the observations within districts are non-independent. Even though the standard errors are larger in this analysis, the three variables that were significant in the OLS analysis are significant in this analysis as well. These standard errors are computed based on aggregate scores for the 37 districts, since these district level scores should be independent. If you have a very small number of clusters compared to your overall sample size it is possible that the standard errors could be quite larger than the OLS results. For example, if there were only 3 districts, the standard errors would be computed on the aggregate scores for just 3 districts.
4.1.3 Robust Regression
The Stata rreg command performs a robust regression using iteratively reweighted least squares, i.e., rreg assigns a weight to each observation with higher weights given to better behaved observations. In fact, extremely deviant cases, those with Cook’s D greater than 1, can have their weights set to missing so that they are not included in the analysis at all.
We will use rreg with the generate option so that we can inspect the weights used to weight the observations. Note that in this analysis both the coefficients and the standard errors differ from the original OLS regression. Below we show the same analysis using robust regression using the rreg command.
rreg api00 acs_k3 acs_46 full enroll, gen(wt)
Robust regression estimates Number of obs = 395
F( 4, 390) = 56.51
Prob > F = 0.0000
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
acs_k3 | 6.110881 4.658131 1.312 0.190 -3.047308 15.26907
acs_46 | 6.254708 1.631587 3.834 0.000 3.046901 9.462516
full | 4.796072 .4414563 10.864 0.000 3.92814 5.664004
enroll | -.1092586 .0287239 -3.804 0.000 -.1657316 -.0527855
_cons | -6.788183 90.5336 -0.075 0.940 -184.7832 171.2068
------------------------------------------------------------------------------
If you compare the robust regression results (directly above) with the OLS results previously presented, you can see that the coefficients and standard errors are quite similar, and the t values and p values are also quite similar. Despite the minor problems that we found in the data when we performed the OLS analysis, the robust regression analysis yielded quite similar results suggesting that indeed these were minor problems. Had the results been substantially different, we would have wanted to further investigate the reasons why the OLS and robust regression results were different, and among the two results the robust regression results would probably be the more trustworthy.
Let’s calculate and look at the predicted (fitted) values (p), the residuals (r), and the leverage (hat) values (h). Note that we are including if e(sample) in the commands because rreg can generate weights of missing and you wouldn’t want to have predicted values and residuals for those observations.
predict p if e(sample) (option xb assumed; fitted values) (5 missing values generated) predict r if e(sample), resid (5 missing values generated) predict h if e(sample), hat (5 missing values generated)
Now, let’s check on the various predicted values and the weighting. First, we will sort by wt then we will look at the first 15 observations. Notice that the smallest weights are near one-half but quickly get into the .7 range.
sort wt
list snum api00 p r h wt in 1/15
snum api00 p r h wt
1. 637 447 733.1567 -286.1568 .0037645 .55612093
2. 5387 892 611.5344 280.4655 .0023925 .57126927
3. 2267 897 621.4881 275.5119 .010207 .58433963
4. 65 903 631.2718 271.7282 .0105486 .59425026
5. 3759 585 842.4838 -257.4838 .0414728 .63063771
6. 5926 469 715.2266 -246.2266 .0058346 .65892631
7. 1978 894 650.7816 243.2184 .0058116 .6665881
8. 3696 483 721.3105 -238.3105 .0052619 .67834344
9. 5222 940 707.648 232.352 .0041016 .69303069
10. 690 424 654.5795 -230.5795 .0094319 .69701005
11. 3785 459 687.3311 -228.3311 .0081474 .70245717
12. 2910 831 604.4401 226.56 .0536809 .70650365
13. 699 437 660.2588 -223.2588 .0059152 .71449402
14. 3070 479 698.1256 -219.1256 .0043322 .72399766
15. 1812 917 698.9828 218.0172 .0099871 .72670695
Now, let’s look at the last 10 observations. The weights for observations 391 to 395 are all very close to one. The values for observations 396 to the end are missing due to the missing predictors. Note that the observations above that have the lowest weights are also those with the largest residuals (residuals over 200) and the observations below with the highest weights have very low residuals (all less than 3).
list snum api00 p r h wt in -10/l
snum api00 p r h wt
391. 3024 727 729.0243 -2.024302 .0104834 .99997367
392. 3535 705 703.846 1.154008 .0048329 .99999207
393. 1885 605 605.427 -.4269809 .0144377 .99999843
394. 1678 497 496.8011 .1989256 .0243301 .99999956
395. 4486 706 705.8076 .192455 .0142448 .99999986
396. 4488 521 . . . .
397. 3072 763 . . . .
398. 3055 590 . . . .
399. 116 513 . . . .
400. 4534 445 . . . .
After using rreg, it is possible to generate predicted values, residuals and leverage (hat), but most of the regression diagnostic commands are not available after rreg. We will have to create some of them for ourselves. Here, of course, is the graph of residuals versus fitted (predicted) with a line at zero. This plot looks much like the OLS plot, except that in the OLS all of the observations would be weighted equally, but as we saw above the observations with the greatest residuals are weighted less and hence have less influence on the results.
graph r p, yline(0)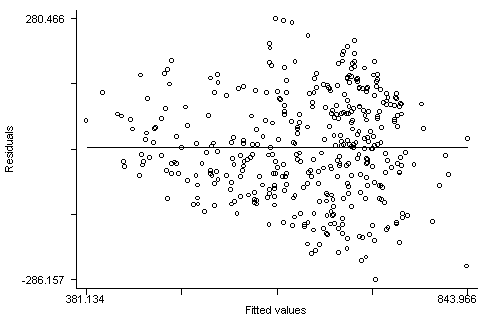
To get an lvr2plot we are going to have to go through several steps in order to get the normalized squared residuals and the means of both the residuals and the leverage (hat) values.
First, we generate the residual squared (r2) and then divide it by the sum of the squared residuals. We then compute the mean of this value and save it as a local macro called rm (which we will use for creating the leverage vs. residual plot).
generate r2=r^2
(5 missing values generated)
sum r2
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
r2 | 395 12436.05 14677.98 .0370389 81885.7
replace r2 = r2/r(sum)
(395 real changes made)
summarize r2
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
r2 | 395 .0025316 .002988 7.54e-09 .0166697
local rm = r(mean)
Next we compute the mean of the leverage and save it as a local macro called hm.
summarize h
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
h | 395 .0126422 .0108228 .0023925 .0664077
local hm = r(mean)
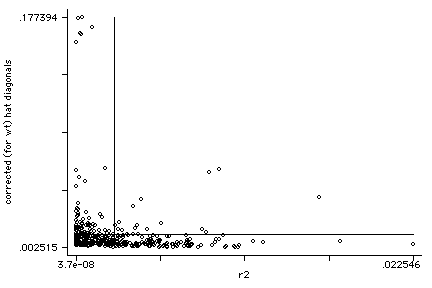
Now, we can plot the leverage against the residual squared as shown below. Comparing the plot below with the plot from the OLS regression, this plot is much better behaved. There are no longer points in the upper right quadrant of the graph.
graph h r2, yline(`hm') xline(`rm')
Let’s close out this analysis by deleting our temporary variables.
drop wt p r h r2
4.1.4 Quantile Regression
Quantile regression, in general, and median regression, in particular, might be considered as an alternative to rreg. The Stata command qreg does quantile regression. qreg without any options will actually do a median regression in which the coefficients will be estimated by minimizing the absolute deviations from the median. Of course, as an estimate of central tendency, the median is a resistant measure that is not as greatly affected by outliers as is the mean. It is not clear that median regression is a resistant estimation procedure, in fact, there is some evidence that it can be affected by high leverage values.
Here is what the quantile regression looks like using Stata’s qreg command. The coefficient and standard error for acs_k3 are considerably different when using qreg as compared to OLS using the regress command (the coefficients are 1.2 vs 6.9 and the standard errors are 6.4 vs 4.3). The coefficients and standard errors for the other variables are also different, but not as dramatically different. Nevertheless, the qreg results indicate that, like the OLS results, all of the variables except acs_k3 are significant.
qreg api00 acs_k3 acs_46 full enroll
Median regression Number of obs = 395
Raw sum of deviations 48534 (about 643)
Min sum of deviations 36268.11 Pseudo R2 = 0.2527
------------------------------------------------------------------------------
api00 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
acs_k3 | 1.269065 6.470588 0.196 0.845 -11.45253 13.99066
acs_46 | 7.22408 2.228949 3.241 0.001 2.841821 11.60634
full | 5.323841 .6157333 8.646 0.000 4.113269 6.534413
enroll | -.1245734 .0397576 -3.133 0.002 -.2027395 -.0464073
_cons | 17.15049 125.4396 0.137 0.891 -229.4719 263.7729
------------------------------------------------------------------------------
The qreg command has even fewer diagnostic options than rreg does. About the only values we can obtain are the predicted values and the residuals.
predict p if e(sample) (option xb assumed; fitted values) (5 missing values generated) predict r if e(sample), r (5 missing values generated) graph r p, yline(0)
Stata has three additional commands that can do quantile regression.
iqreg estimates interquantile regressions, regressions of the difference in quantiles. The estimated variance-covariance matrix of the estimators is obtained via bootstrapping.
sqreg estimates simultaneous-quantile regression. It produces the same coefficients as qreg for each quantile. sqreg obtains a bootstrapped variance-covariance matrix of the estimators that includes between-quantiles blocks. Thus, one can test and construct confidence intervals comparing coefficients describing different quantiles.
bsqreg is the same as sqreg with one quantile. sqreg is, therefore, faster than bsqreg.
4.2 Constrained Linear Regression
Let’s begin this section by looking at a regression model using the hsb2 dataset. The hsb2 file is a sample of 200 cases from the Highschool and Beyond Study (Rock, Hilton, Pollack, Ekstrom & Goertz, 1985). It includes the following variables: id, female, race, ses, schtyp, program, read, write, math, science and socst. The variables read, write, math, science and socst are the results of standardized tests on reading, writing, math, science and social studies (respectively), and the variable female is coded 1 if female, 0 if male.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2
Let’s start by doing an OLS regression where we predict socst score from read, write, math, science and female (gender)
regress socst read write math science female
Source | SS df MS Number of obs = 200
---------+------------------------------ F( 5, 194) = 35.44
Model | 10949.2575 5 2189.8515 Prob > F = 0.0000
Residual | 11986.9375 194 61.7883375 R-squared = 0.4774
---------+------------------------------ Adj R-squared = 0.4639
Total | 22936.195 199 115.257261 Root MSE = 7.8606
------------------------------------------------------------------------------
socst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .3784046 .0806267 4.693 0.000 .2193872 .537422
write | .3858743 .0889283 4.339 0.000 .2104839 .5612646
math | .1303258 .0893767 1.458 0.146 -.045949 .3066006
science | -.0333925 .0818741 -0.408 0.684 -.1948702 .1280852
female | -.3532648 1.245372 -0.284 0.777 -2.809471 2.102941
_cons | 7.339342 3.650243 2.011 0.046 .1400864 14.5386
------------------------------------------------------------------------------
Notice that the coefficients for read and write are very similar, which makes sense since they are both measures of language ability. Also, the coefficients for math and science are similar (in that they are both not significantly different from 0). Suppose that we have a theory that suggests that read and write should have equal coefficients, and that math and science should have equal coefficients as well. We can test the equality of the coefficients using the test command.
test read=write
( 1) read - write = 0.0
F( 1, 194) = 0.00
Prob > F = 0.9558
We can also do this with the testparm command, which is especially useful if you were testing whether 3 or more coefficients were equal.
testparm read write, equal
( 1) - read + write = 0.0
F( 1, 194) = 0.00
Prob > F = 0.9558
Both of these results indicate that there is no significant difference in the coefficients for the reading and writing scores. Since it appears that the coefficients for math and science are also equal, let’s test the equality of those as well (using the testparm command).
testparm math science, equal
( 1) - math + science = 0.0
F( 1, 194) = 1.45
Prob > F = 0.2299
Let’s now perform both of these tests together, simultaneously testing that the coefficient for read equals write and math equals science. We do this using two test commands, the second using the accum option to accumulate the first test with the second test to test both of these hypotheses together.
test read=write
( 1) read - write = 0.0
F( 1, 194) = 0.00
Prob > F = 0.9558
test math=science, accum
( 1) read - write = 0.0
( 2) math - science = 0.0
F( 2, 194) = 0.73
Prob > F = 0.4852
Note this second test has 2 df, since it is testing both of the hypotheses listed, and this test is not significant, suggesting these pairs of coefficients are not significantly different from each other. We can estimate regression models where we constrain coefficients to be equal to each other. For example, let’s begin on a limited scale and constrain read to equal write. First, we will define a constraint and then we will run the cnsreg command.
constraint define 1 read = write
. cnsreg socst read write math science female, constraint(1)
Constrained linear regression Number of obs = 200
F( 4, 195) = 44.53
Prob > F = 0.0000
Root MSE = 7.8404
( 1) read - write = 0.0
------------------------------------------------------------------------------
socst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .3818488 .0513899 7.430 0.000 .2804975 .4832002
write | .3818488 .0513899 7.430 0.000 .2804975 .4832002
math | .1303036 .0891471 1.462 0.145 -.0455126 .3061197
science | -.0332762 .0816379 -0.408 0.684 -.1942827 .1277303
female | -.3296237 1.167364 -0.282 0.778 -2.631904 1.972657
_cons | 7.354148 3.631175 2.025 0.044 .1927294 14.51557
------------------------------------------------------------------------------
Notice that the coefficients for read and write are identical, along with their standard errors, t-test, etc. Also note that the degrees of freedom for the F test is four, not five, as in the OLS model. This is because only one coefficient is estimated for read and write, estimated like a single variable equal to the sum of their values. Notice also that the Root MSE is slightly higher for the constrained model, but only slightly higher. This is because we have forced the model to estimate the coefficients for read and write that are not as good at minimizing the Sum of Squares Error (the coefficients that would minimize the SSE would be the coefficients from the unconstrained model).
Next, we will define a second constraint, setting math equal to science. We will also abbreviate the constraints option to c.
constraint define 2 math = science
. cnsreg socst read write math science female, c(1 2)
Constrained linear regression Number of obs = 200
F( 3, 196) = 58.75
Prob > F = 0.0000
Root MSE = 7.8496
( 1) read - write = 0.0
( 2) math - science = 0.0
------------------------------------------------------------------------------
socst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .3860376 .0513322 7.520 0.000 .2848033 .4872719
write | .3860376 .0513322 7.520 0.000 .2848033 .4872719
math | .0428053 .0519238 0.824 0.411 -.0595958 .1452064
science | .0428053 .0519238 0.824 0.411 -.0595958 .1452064
female | -.200875 1.163831 -0.173 0.863 -2.496114 2.094364
_cons | 7.505658 3.633225 2.066 0.040 .3404249 14.67089
------------------------------------------------------------------------------
Now the coefficients for read = write and math = science and the degrees of freedom for the model has dropped to three. Again, the Root MSE is slightly larger than in the prior model, but we should emphasize only very slightly larger. If indeed the population coefficients for read = write and math = science, then these combined (constrained) estimates may be more stable and generalize better to other samples. So although these estimates may lead to slightly higher standard error of prediction in this sample, they may generalize better to the population from which they came.
4.3 Regression with Censored or Truncated Data
Analyzing data that contain censored values or are truncated is common in many research disciplines. According to Hosmer and Lemeshow (1999), a censored value is one whose value is incomplete due to random factors for each subject. A truncated observation, on the other hand, is one which is incomplete due to a selection process in the design of the study.
We will begin by looking at analyzing data with censored values.
4.3.1 Regression with Censored Data
In this example we have a variable called acadindx which is a weighted combination of standardized test scores and academic grades. The maximum possible score on acadindx is 200 but it is clear that the 16 students who scored 200 are not exactly equal in their academic abilities. In other words, there is variability in academic ability that is not being accounted for when students score 200 on acadindx. The variable acadindx is said to be censored, in particular, it is right censored.
Let’s look at the example. We will begin by looking at a description of the data, some descriptive statistics, and correlations among the variables.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/acadindx
(max possible on acadindx is 200)
describe
Contains data from acadindx.dta
obs: 200 max possible on acadindx is 200
vars: 5 19 Jan 2001 20:14
size: 4,800 (99.7% of memory free)
-------------------------------------------------------------------------------
1. id float %9.0g
2. female float %9.0g fl
3. reading float %9.0g
4. writing float %9.0g
5. acadindx float %9.0g academic index
-------------------------------------------------------------------------------
summarize
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
id | 200 100.5 57.87918 1 200
female | 200 .545 .4992205 0 1
reading | 200 52.23 10.25294 28 76
writing | 200 52.775 9.478586 31 67
acadindx | 200 172.185 16.8174 138 200
count if acadindx==200
16
corr acadindx female reading writing
(obs=200)
| acadindx female reading writing
---------+------------------------------------
acadindx | 1.0000
female | -0.0821 1.0000
reading | 0.7131 -0.0531 1.0000
writing | 0.6626 0.2565 0.5968 1.0000
Now, let’s run a standard OLS regression on the data and generate predicted scores in p1.
regress acadindx female reading writing Source | SS df MS Number of obs = 200 ---------+------------------------------ F( 3, 196) = 107.40 Model | 34994.282 3 11664.7607 Prob > F = 0.0000 Residual | 21287.873 196 108.611597 R-squared = 0.6218 ---------+------------------------------ Adj R-squared = 0.6160 Total | 56282.155 199 282.824899 Root MSE = 10.422 ------------------------------------------------------------------------------ acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- female | -5.832498 1.58821 -3.672 0.000 -8.964671 -2.700324 reading | .7184174 .0931493 7.713 0.000 .5347138 .902121 writing | .7905706 .1040996 7.594 0.000 .5852715 .9958696 _cons | 96.11841 4.489562 21.409 0.000 87.26436 104.9725 ------------------------------------------------------------------------------ predict p1 (option xb assumed; fitted values)
The tobit command is one of the commands that can be used for regression with censored data. The syntax of the command is similar to regress with the addition of the ul option to indicate that the right censored value is 200. We will follow the tobit command by predicting p2 containing the tobit predicted values.
tobit acadindx female reading writing, ul(200)
Tobit estimates Number of obs = 200
LR chi2(3) = 190.39
Prob > chi2 = 0.0000
Log likelihood = -718.06362 Pseudo R2 = 0.1171
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
female | -6.347316 1.692441 -3.750 0.000 -9.684943 -3.009688
reading | .7776857 .0996928 7.801 0.000 .5810837 .9742877
writing | .8111221 .110211 7.360 0.000 .5937773 1.028467
_cons | 92.73782 4.803441 19.307 0.000 83.26506 102.2106
---------+--------------------------------------------------------------------
_se | 10.98973 .5817477 (Ancillary parameter)
------------------------------------------------------------------------------
Obs. summary: 184 uncensored observations
16 right-censored observations at acadindx>=200
predict p2
(option xb assumed; fitted values)
Summarizing the p1 and p2 scores shows that the tobit predicted values have a larger standard deviation and a greater range of values.
summarize acadindx p1 p2
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
acadindx | 200 172.185 16.8174 138 200
p1 | 200 172.185 13.26087 142.3821 201.5311
p2 | 200 172.704 14.00292 141.2211 203.8541
When we look at a listing of p1 and p2 for all students who scored the maximum of 200 on acadindx, we see that in every case the tobit predicted value is greater than the OLS predicted value. These predictions represent an estimate of what the variability would be if the values of acadindx could exceed 200.
list p1 p2 if acadindx==200
p1 p2
32. 179.175 179.62
57. 192.6806 194.3291
68. 201.5311 203.8541
80. 191.8309 193.577
82. 188.1537 189.5627
88. 186.5725 187.9405
95. 195.9971 198.1762
100. 186.9333 188.1076
132. 197.5782 199.7984
136. 189.4592 191.1436
143. 191.1846 192.8327
157. 191.6145 193.4767
161. 180.2511 181.0082
169. 182.275 183.3667
174. 191.6145 193.4767
200. 187.6616 189.4211
Here is the syntax diagram for tobit:
tobit depvar [indepvars] [weight] [if exp] [in range], ll[(#)] ul[(#)] [ level(#) offset(varname) maximize_options ]
You can declare both lower and upper censored values. The censored values are fixed in that the same lower and upper values apply to all observations.
There are two other commands in Stata that allow you more flexibility in doing regression with censored data.
cnreg estimates a model in which the censored values may vary from observation to observation.
intreg estimates a model where the response variable for each observation is either point data, interval data, left-censored data, or right-censored data.
4.3.2 Regression with Truncated Data
Truncated data occurs when some observations are not included in the analysis because of the value of the variable. We will illustrate analysis with truncation using the dataset, acadindx, that was used in the previous section. If acadindx is no longer loaded in memory you can get it with the following use command.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/acadindx (max possible on acadindx is 200)
Let’s imagine that in order to get into a special honors program, students need to score at least 160 on acadindx. So we will drop all observations in which the value of acadindx is less than 160.
drop if acadindx <= 160 (56 observations deleted)
Now, let’s estimate the same model that we used in the section on censored data, only this time we will pretend that a 200 for acadindx is not censored.
regress acadindx female reading writing
Source | SS df MS Number of obs = 144
-------------+------------------------------ F( 3, 140) = 33.01
Model | 8074.79638 3 2691.59879 Prob > F = 0.0000
Residual | 11416.3633 140 81.5454524 R-squared = 0.4143
-------------+------------------------------ Adj R-squared = 0.4017
Total | 19491.1597 143 136.301816 Root MSE = 9.0303
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -5.238495 1.615632 -3.24 0.001 -8.432687 -2.044303
reading | .4411066 .0963504 4.58 0.000 .2506166 .6315965
writing | .5873287 .1150828 5.10 0.000 .3598037 .8148537
_cons | 125.6355 5.891559 21.32 0.000 113.9875 137.2834
------------------------------------------------------------------------------
It is clear that the estimates of the coefficients are distorted due to the fact that 56 observations are no longer in the dataset. This amounts to restriction of range on both the response variable and the predictor variables. For example, the coefficient for writing dropped from .79 to .59. What this means is that if our goal is to find the relation between adadindx and the predictor variables in the population, then the truncation of acadindx in our sample is going to lead to biased estimates. A better approach to analyzing these data is to use truncated regression. In Stata this can be accomplished using the truncreg command where the ll option is used to indicate the lower limit of acadindx scores used in the truncation.
truncreg acadindx female reading writing, ll(160)
(note: 0 obs. truncated)
Truncated regression
Limit: lower = 160 Number of obs = 144
upper = +inf Wald chi2(3) = 77.87
Log likelihood = -510.00768 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
eq1 |
female | -6.099602 1.925245 -3.17 0.002 -9.873012 -2.326191
reading | .5181789 .1168288 4.44 0.000 .2891986 .7471592
writing | .7661636 .15262 5.02 0.000 .4670339 1.065293
_cons | 110.2892 8.673849 12.72 0.000 93.28877 127.2896
-------------+----------------------------------------------------------------
sigma |
_cons | 9.803572 .721646 13.59 0.000 8.389172 11.21797
------------------------------------------------------------------------------
The coefficients from the truncreg command are closer to the OLS results, for example the coefficient for writing is .77 which is closer to the OLS results of .79. However, the results are still somewhat different on the other variables, for example the coefficient for reading is .52 in the truncreg as compared to .72 in the original OLS with the unrestricted data, and better than the OLS estimate of .47 with the restricted data. While truncreg may improve the estimates on a restricted data file as compared to OLS, it is certainly no substitute for analyzing the complete unrestricted data file.
4.4 Regression with Measurement Error
As you will most likely recall, one of the assumptions of regression is that the predictor variables are measured without error. The problem is that measurement error in predictor variables leads to under estimation of the regression coefficients. Stata’s eivreg command takes measurement error into account when estimating the coefficients for the model.
Let’s look at a regression using the hsb2 dataset.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2
regress write read female
Source | SS df MS Number of obs = 200
---------+------------------------------ F( 2, 197) = 77.21
Model | 7856.32118 2 3928.16059 Prob > F = 0.0000
Residual | 10022.5538 197 50.8759077 R-squared = 0.4394
---------+------------------------------ Adj R-squared = 0.4337
Total | 17878.875 199 89.843593 Root MSE = 7.1327
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .5658869 .0493849 11.459 0.000 .468496 .6632778
female | 5.486894 1.014261 5.410 0.000 3.48669 7.487098
_cons | 20.22837 2.713756 7.454 0.000 14.87663 25.58011
------------------------------------------------------------------------------
The predictor read is a standardized test score. Every test has measurement error. We don’t know the exact reliability of read, but using .9 for the reliability would probably not be far off. We will now estimate the same regression model with the Stata eivreg command, which stands for errors-in-variables regression.
eivreg write read female, r(read .9)
assumed errors-in-variables regression
variable reliability
------------------------ Number of obs = 200
read 0.9000 F( 2, 197) = 83.41
* 1.0000 Prob > F = 0.0000
R-squared = 0.4811
Root MSE = 6.86268
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .6289607 .0528111 11.910 0.000 .524813 .7331085
female | 5.555659 .9761838 5.691 0.000 3.630548 7.48077
_cons | 16.89655 2.880972 5.865 0.000 11.21504 22.57805
Note that the F-ratio and the R2 increased along with the regression coefficient for read. Additionally, there is an increase in the standard error for read.
Now, let’s try a model with read, math and socst as predictors. First, we will run a standard OLS regression.
regress write read math socst female
Source | SS df MS Number of obs = 200
---------+------------------------------ F( 4, 195) = 64.37
Model | 10173.7036 4 2543.42591 Prob > F = 0.0000
Residual | 7705.17137 195 39.5136993 R-squared = 0.5690
---------+------------------------------ Adj R-squared = 0.5602
Total | 17878.875 199 89.843593 Root MSE = 6.286
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .2065341 .0640006 3.227 0.001 .0803118 .3327563
math | .3322639 .0651838 5.097 0.000 .2037082 .4608195
socst | .2413236 .0547259 4.410 0.000 .133393 .3492542
female | 5.006263 .8993625 5.566 0.000 3.232537 6.77999
_cons | 9.120717 2.808367 3.248 0.001 3.582045 14.65939
------------------------------------------------------------------------------
Now, let’s try to account for the measurement error by using the following reliabilities: read – .9, math – .9, socst – .8.
eivreg write read math socst female, r(read .9 math .9 socst .8)
assumed errors-in-variables regression
variable reliability
------------------------ Number of obs = 200
read 0.9000 F( 4, 195) = 70.17
math 0.9000 Prob > F = 0.0000
socst 0.8000 R-squared = 0.6047
* 1.0000 Root MSE = 6.02062
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .1506668 .0936571 1.609 0.109 -.0340441 .3353776
math | .350551 .0850704 4.121 0.000 .1827747 .5183273
socst | .3327103 .0876869 3.794 0.000 .159774 .5056467
female | 4.852501 .8730646 5.558 0.000 3.13064 6.574363
_cons | 6.37062 2.868021 2.221 0.027 .7142973 12.02694
------------------------------------------------------------------------------
Note that the overall F and R2 went up, but that the coefficient for read is no longer statistically significant.
4.5 Multiple Equation Regression Models
If a dataset has enough variables we may want to estimate more than one regression model. For example, we may want to predict y1 from x1 and also predict y2 from x2. Even though there are no variables in common these two models are not independent of one another because the data come from the same subjects. This is an example of one type of multiple equation regression known as seemingly unrelated regression. We can estimate the coefficients and obtain standard errors taking into account the correlated errors in the two models. An important feature of multiple equation models is that we can test predictors across equations.
Another example of multiple equation regression is if we wished to predict y1, y2 and y3 from x1 and x2. This is a three equation system, known as multivariate regression, with the same predictor variables for each model. Again, we have the capability of testing coefficients across the different equations.
Multiple equation models are a powerful extension to our data analysis tool kit.
4.5.1 Seemingly Unrelated Regression
Let’s continue using the hsb2 data file to illustrate the use of seemingly unrelated regression. You can load it into memory again if it has been cleared out.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2 (highschool and beyond (200 cases))
This time let’s look at two regression models.
science = math female
write = read female
It is the case that the errors (residuals) from these two models would be correlated. This would be true even if the predictor female were not found in both models. The errors would be correlated because all of the values of the variables are collected on the same set of observations. This is a situation tailor made for seemingly unrelated regression using the sureg command. Here is our first model using OLS.
regress science math female
<some output omitted>
------------------------------------------------------------------------------
science | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
math | .6631901 .0578724 11.460 0.000 .549061 .7773191
female | -2.168396 1.086043 -1.997 0.047 -4.310159 -.026633
_cons | 18.11813 3.167133 5.721 0.000 11.8723 24.36397
------------------------------------------------------------------------------
And here is our second model using OLS.
regress write read female
<some output omitted>
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read | .5658869 .0493849 11.459 0.000 .468496 .6632778
female | 5.486894 1.014261 5.410 0.000 3.48669 7.487098
_cons | 20.22837 2.713756 7.454 0.000 14.87663 25.58011
------------------------------------------------------------------------------
With the sureg command we can estimate both models simultaneously while accounting for the correlated errors at the same time, leading to efficient estimates of the coefficients and standard errors. By including the corr option with sureg we can also obtain an estimate of the correlation between the errors of the two models. Note that both the estimates of the coefficients and their standard errors are different from the OLS model estimates shown above. The bottom of the output provides a Breusch-Pagan test of whether the residuals from the two equations are independent (in this case, we would say the residuals were not independent, p=0.0407).
sureg (science math female) (write read female), corr
Seemingly unrelated regression
------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" Chi2 P
------------------------------------------------------------------
science 200 2 7.595793 0.4085 125.4142 0.0000
write 200 2 7.085844 0.4383 144.2683 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
science |
math | .6251409 .0570948 10.949 0.000 .5132373 .7370446
female | -2.189344 1.077862 -2.031 0.042 -4.301914 -.0767744
_cons | 20.13265 3.125775 6.441 0.000 14.00624 26.25905
---------+--------------------------------------------------------------------
write |
read | .5354838 .0487212 10.991 0.000 .4399919 .6309757
female | 5.453748 1.006609 5.418 0.000 3.48083 7.426665
_cons | 21.83439 2.67851 8.152 0.000 16.5846 27.08417
------------------------------------------------------------------------------
Correlation matrix of residuals:
science write
science 1.0000
write 0.1447 1.0000
Breusch-Pagan test of independence: chi2(1) = 4.188, Pr = 0.0407
Now that we have estimated our models let’s test the predictor variables. The test for female combines information from both models. The tests for math and read are actually equivalent to the z-tests above except that the results are displayed as chi-square tests.
test female
( 1) [science]female = 0.0
( 2) [write]female = 0.0
chi2( 2) = 37.45
Prob > chi2 = 0.0000
test math
( 1) [science]math = 0.0
chi2( 1) = 119.88
Prob > chi2 = 0.0000
test read
( 1) [write]read = 0.0
chi2( 1) = 120.80
Prob > chi2 = 0.0000
Now, let’s estimate 3 models where we use the same predictors in each model as shown below.
read = female prog1 prog3
write = female prog1 prog3
math = female prog1 prog3
If you no longer have the dummy variables for prog, you can recreate them using the tabulate command.
tabulate prog, gen(prog)
Let’s first estimate these three models using 3 OLS regressions.
regress read female prog1 prog3
<some output omitted>
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
female | -1.208582 1.327672 -0.910 0.364 -3.826939 1.409774
prog1 | -6.42937 1.665893 -3.859 0.000 -9.714746 -3.143993
prog3 | -9.976868 1.606428 -6.211 0.000 -13.14497 -6.808765
_cons | 56.8295 1.170562 48.549 0.000 54.52099 59.13802
------------------------------------------------------------------------------
regress write female prog1 prog3
<some output omitted>
------------------------------------------------------------------------------
write | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
female | 4.771211 1.181876 4.037 0.000 2.440385 7.102037
prog1 | -4.832929 1.482956 -3.259 0.001 -7.757528 -1.908331
prog3 | -9.438071 1.430021 -6.600 0.000 -12.25827 -6.617868
_cons | 53.62162 1.042019 51.459 0.000 51.56661 55.67662
------------------------------------------------------------------------------
regress math female prog1 prog3
<some output omitted>
------------------------------------------------------------------------------
math | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
female | -.6737673 1.176059 -0.573 0.567 -2.993122 1.645587
prog1 | -6.723945 1.475657 -4.557 0.000 -9.634149 -3.81374
prog3 | -10.32168 1.422983 -7.254 0.000 -13.128 -7.515352
_cons | 57.10551 1.03689 55.074 0.000 55.06062 59.1504
------------------------------------------------------------------------------
These regressions provide fine estimates of the coefficients and standard errors but these results assume the residuals of each analysis are completely independent of the others. Also, if we wish to test female, we would have to do it three times and would not be able to combine the information from all three tests into a single overall test.
Now let’s use sureg to estimate the same models. Since all 3 models have the same predictors, we can use the syntax as shown below which says that read, write and math will each be predicted by female, prog1 and prog3. Note that the coefficients are identical in the OLS results above and the sureg results below, however the standard errors are different, only slightly, due to the correlation among the residuals in the multiple equations.
sureg (read write math = female prog1 prog3), corr
Seemingly unrelated regression
------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" Chi2 P
------------------------------------------------------------------
read 200 3 9.254765 0.1811 44.24114 0.0000
write 200 3 8.238468 0.2408 63.41908 0.0000
math 200 3 8.197921 0.2304 59.88479 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read |
female | -1.208582 1.314328 -0.920 0.358 -3.784618 1.367454
prog1 | -6.42937 1.64915 -3.899 0.000 -9.661645 -3.197095
prog3 | -9.976868 1.590283 -6.274 0.000 -13.09377 -6.859971
_cons | 56.8295 1.158797 49.042 0.000 54.5583 59.1007
---------+--------------------------------------------------------------------
write |
female | 4.771211 1.169997 4.078 0.000 2.478058 7.064363
prog1 | -4.832929 1.468051 -3.292 0.001 -7.710257 -1.955602
prog3 | -9.438071 1.415648 -6.667 0.000 -12.21269 -6.663451
_cons | 53.62162 1.031546 51.982 0.000 51.59982 55.64341
---------+--------------------------------------------------------------------
math |
female | -.6737673 1.164239 -0.579 0.563 -2.955634 1.608099
prog1 | -6.723945 1.460826 -4.603 0.000 -9.587111 -3.860778
prog3 | -10.32168 1.408681 -7.327 0.000 -13.08264 -7.560711
_cons | 57.10551 1.026469 55.633 0.000 55.09367 59.11735
------------------------------------------------------------------------------
Correlation matrix of residuals:
read write math
read 1.0000
write 0.5519 1.0000
math 0.5774 0.5577 1.0000
Breusch-Pagan test of independence: chi2(3) = 189.811, Pr = 0.0000
In addition to getting more appropriate standard errors, sureg allows us to test the effects of the predictors across the equations. We can test the hypothesis that the coefficient for female is 0 for all three outcome variables, as shown below.
test female
( 1) [read]female = 0.0
( 2) [write]female = 0.0
( 3) [math]female = 0.0
chi2( 3) = 35.59
Prob > chi2 = 0.0000
We can also test the hypothesis that the coefficient for female is 0 for just read and math. Note that [read]female means the coefficient for female for the outcome variable read.
test [read]female [math]female
( 1) [read]female = 0.0
( 2) [math]female = 0.0
chi2( 2) = 0.85
Prob > chi2 = 0.6541
We can also test the hypothesis that the coefficients for prog1 and prog3 are 0 for all three outcome variables, as shown below.
test prog1 prog3
( 1) [read]prog1 = 0.0
( 2) [write]prog1 = 0.0
( 3) [math]prog1 = 0.0
( 4) [read]prog3 = 0.0
( 5) [write]prog3 = 0.0
( 6) [math]prog3 = 0.0
chi2( 6) = 72.45
Prob > chi2 = 0.0000
4.5.2 Multivariate Regression
Let’s now use multivariate regression using the mvreg command to look at the same analysis that we saw in the sureg example above, estimating the following 3 models.
read = female prog1 prog3
write = female prog1 prog3
math = female prog1 prog3
If you don’t have the hsb2 data file in memory, you can use it below and then create the dummy variables for prog1 – prog3.
use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2 tabulate prog, gen(prog) <output omitted>
Below we use mvreg to predict read, write and math from female, prog1 and prog3. Note that the top part of the output is similar to the sureg output in that it gives an overall summary of the model for each outcome variable, however the results are somewhat different and the sureg uses a Chi-Square test for the overall fit of the model, and mvreg uses an F-test. The lower part of the output appears similar to the sureg output; however, when you compare the standard errors you see that the results are not the same. These standard errors correspond to the OLS standard errors, so these results below do not take into account the correlations among the residuals (as do the sureg results).
mvreg read write math = female prog1 prog3
Equation Obs Parms RMSE "R-sq" F P
------------------------------------------------------------------
read 200 4 9.348725 0.1811 14.45211 0.0000
write 200 4 8.32211 0.2408 20.7169 0.0000
math 200 4 8.281151 0.2304 19.56237 0.0000
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
read |
female | -1.208582 1.327672 -0.910 0.364 -3.826939 1.409774
prog1 | -6.42937 1.665893 -3.859 0.000 -9.714746 -3.143993
prog3 | -9.976868 1.606428 -6.211 0.000 -13.14497 -6.808765
_cons | 56.8295 1.170562 48.549 0.000 54.52099 59.13802
---------+--------------------------------------------------------------------
write |
female | 4.771211 1.181876 4.037 0.000 2.440385 7.102037
prog1 | -4.832929 1.482956 -3.259 0.001 -7.757528 -1.908331
prog3 | -9.438071 1.430021 -6.600 0.000 -12.25827 -6.617868
_cons | 53.62162 1.042019 51.459 0.000 51.56661 55.67662
---------+--------------------------------------------------------------------
math |
female | -.6737673 1.176059 -0.573 0.567 -2.993122 1.645587
prog1 | -6.723945 1.475657 -4.557 0.000 -9.634149 -3.81374
prog3 | -10.32168 1.422983 -7.254 0.000 -13.128 -7.515352
_cons | 57.10551 1.03689 55.074 0.000 55.06062 59.1504
------------------------------------------------------------------------------
Now, let’s test female. Note, that female was statistically significant in only one of the three equations. Using the test command after mvreg allows us to test female across all three equations simultaneously. And, guess what? It is significant. This is consistent with what we found using sureg (except that sureg did this test using a Chi-Square test).
test female
( 1) [read]female = 0.0
( 2) [write]female = 0.0
( 3) [math]female = 0.0
F( 3, 196) = 11.63
Prob > F = 0.0000
We can also test prog1 and prog3, both separately and combined. Remember these are multivariate tests.
test prog1
( 1) [read]prog1 = 0.0
( 2) [write]prog1 = 0.0
( 3) [math]prog1 = 0.0
F( 3, 196) = 7.72
Prob > F = 0.0001
test prog3
( 1) [read]prog3 = 0.0
( 2) [write]prog3 = 0.0
( 3) [math]prog3 = 0.0
F( 3, 196) = 21.47
Prob > F = 0.0000
test prog1 prog3
( 1) [read]prog1 = 0.0
( 2) [write]prog1 = 0.0
( 3) [math]prog1 = 0.0
( 4) [read]prog3 = 0.0
( 5) [write]prog3 = 0.0
( 6) [math]prog3 = 0.0
F( 6, 196) = 11.83
Prob > F = 0.0000
Many researchers familiar with traditional multivariate analysis may not recognize the tests above. They don’t see Wilks’ Lambda, Pillai’s Trace or the Hotelling-Lawley Trace statistics, statistics that they are familiar with. It is possible to obtain these statistics using the mvtest command written by David E. Moore of the University of Cincinnati. mvtest , which UCLA updated to work with Stata 6 and above, can be downloaded over the internet like this.
net from https://stats.idre.ucla.edu/stat/stata/ado/analysis net install mvtest
Now that we have downloaded it, we can use it like this.
mvtest female
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "female" Effect(s)
S=1 M=.5 N=96
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.84892448 11.5081 3 194.0000 0.0000
Pillai's Trace 0.15107552 11.5081 3 194.0000 0.0000
Hotelling-Lawley Trace 0.17796108 11.5081 3 194.0000 0.0000
mvtest prog1 prog3
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "prog1 prog3" Effect(s)
S=2 M=0 N=96
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.73294667 10.8676 6 388.0000 0.0000
Pillai's Trace 0.26859190 10.0834 6 390.0000 0.0000
Hotelling-Lawley Trace 0.36225660 11.6526 6 386.0000 0.0000
We will end with an mvtest including all of the predictor variables. This is an overall multivariate test of the model.
mvtest female prog1 prog3
MULTIVARIATE TESTS OF SIGNIFICANCE
Multivariate Test Criteria and Exact F Statistics for
the Hypothesis of no Overall "female prog1 prog3" Effect(s)
S=3 M=-.5 N=96
Test Value F Num DF Den DF Pr > F
Wilks' Lambda 0.62308940 11.2593 9 472.2956 0.0000
Pillai's Trace 0.41696769 10.5465 9 588.0000 0.0000
Hotelling-Lawley Trace 0.54062431 11.5734 9 578.0000 0.0000
The sureg and mvreg commands both allow you to test multi-equation models while taking into account the fact that the equations are not independent. The sureg command allows you to get estimates for each equation which adjust for the non-independence of the equations, and it allows you to estimate equations which don’t necessarily have the same predictors. By contrast, mvreg is restricted to equations that have the same set of predictors, and the estimates it provides for the individual equations are the same as the OLS estimates. However, mvreg (especially when combined with mvtest) allows you to perform more traditional multivariate tests of predictors.
4.6 Summary
This chapter has covered a variety of topics that go beyond ordinary least squares regression, but there still remain a variety of topics we wish we could have covered, including the analysis of survey data, dealing with missing data, panel data analysis, and more. And, for the topics we did cover, we wish we could have gone into even more detail. One of our main goals for this chapter was to help you be aware of some of the techniques that are available in Stata for analyzing data that do not fit the assumptions of OLS regression and some of the remedies that are possible. If you are a member of the UCLA research community, and you have further questions, we invite you to use our consulting services to discuss issues specific to your data analysis.
4.7 Self Assessment
1. Use the crime data file that was used in chapter 2 (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/crime ) and look at a regression model predicting murder from pctmetro, poverty, pcths and single using OLS and make a avplots and a lvr2plot following the regression. Are there any states that look worrisome? Repeat this analysis using regression with robust standard errors and show avplots for the analysis. Repeat the analysis using robust regression and make a manually created lvr2plot. Also run the results using qreg. Compare the results of the different analyses. Look at the weights from the robust regression and comment on the weights.
2. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) pretend that 550 is the lowest score that a school could achieve on api00, i.e., create a new variable with the api00 score and recode it such that any score of 550 or below becomes 550. Use meals, ell and emer to predict api scores using 1) OLS to predict the original api score (before recoding) 2) OLS to predict the recoded score where 550 was the lowest value, and 3) using tobit to predict the recoded api score indicating the lowest value is 550. Compare the results of these analyses.
3. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) pretend that only schools with api scores of 550 or higher were included in the sample. Use meals, ell and emer to predict api scores using 1) OLS to predict api from the full set of observations, 2) OLS to predict api using just the observations with api scores of 550 or higher, and 3) using truncreg to predict api using just the observations where api is 550 or higher. Compare the results of these analyses.
4. Using the hsb2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/hsb2 ) predict read from science, socst, math and write. Use the testparm and test commands to test the equality of the coefficients for science, socst and math. Use cnsreg to estimate a model where these three parameters are equal.
5. Using the elemapi2 data file (use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/elemapi2 ) consider the following 2 regression equations.
api00 = meals ell emer api99 = meals ell emer
Estimate the coefficients for these predictors in predicting api00 and api99 taking into account the non-independence of the schools. Test the overall contribution of each of the predictors in jointly predicting api scores in these two years. Test whether the contribution of emer is the same for api00 and api99.
Click here for our answers to these self assessment questions.
4.8 For more information
- Stata Manuals
- [R] rreg
- [R] qreg
- [R] cnsreg
- [R] tobit
- [R] truncreg
- [R] eivreg
- [R] sureg
- [R] mvreg
- [U] 23 Estimation and post-estimation commands
- [U] 29 Overview of model estimation in Stata
- Web Links