2.0 Introduction
2.1 One Categorical predictor
2.2 Two Categorical predictors
2.2.1 A 2 by 2 Layout with Only Main Effects
2.2.2 A 2 by 2 Layout with Main Effects and Interaction
2.2.3 A 2 by 3 Layout with Only Main Effects
2.2.4 A 2 by 3 Layout with Main Effects and Interaction
2.3 Categorical and Continuous Predictors
2.3.1 A Continuous and a Two Level Categorical Predictor
2.3.2 A Continuous and a Two Level Categorical Predictor with Interaction
2.3.3 A Continuous and a Three Level Categorical Predictor
2.3.4 A Continuous and a Three Level Categorical Predictor with Interaction
2.4 More on Interpreting Coefficients and Odds Ratios
2.5 Summary
NOTE: This page is under construction!!
2.0 Introduction
In the previous chapter, we looked at logistic regression analyses that used a categorical predictor with 2 levels (i.e. a dummy variable) and a predictor that was continuous. In this chapter, we will further explore the use of categorical predictors, including using categorical predictors with more than 2 levels, 2 categorical predictors, interactions of categorical predictors, and interactions of categorical predictors with continuous predictors. We will focus on the understanding and interpretation of the results of these analyses. We hope that you are familiar with the use of categorical predictors in ordinary least squares (OLS) regression, as described in Chapter 3 of the Regression with Stata book. Understanding how to interpret the results from OLS regression will be a great help in understanding results from similar analyses involving logistic regression.
This chapter will use the apilog data that you have seen in the prior chapters. We will focus on four variables hiqual as the outcome variable, and three predictors, the proportion of teachers with full teaching credentials (cred), the level of education of the parents (pared), and the percentage of students in the school receiving free meals (meals). Below we show how you can load this data file from within Stata.
use https://stats.idre.ucla.edu/stat/stata/webbooks/logistic/apilog, clear
2.1 One Categorical Predictor
First, let’s look at what happens when we use one categorical predictor with three levels. The predictor that we will use is based on the proportion of teachers who have full credentials. We have divided the schools into 3 categories, schools that have a low percentage of teachers with full credentials, schools with a medium percentage of teachers with full credentials and schools with a high percentage of teachers with full credentials. We will refer to these schools as high credentialed, medium credentialed and low credentialed schools. Below we show the codebook information for this variable. The variable cred is coded 1, 2 and 3 representing low, medium and high respectively.
codebook cred
cred ----------------------------------------- Full Credent Teachers, Lo Med Hi
type: numeric (byte)
label: lmh
range: [1,3] units: 1
unique values: 3 coded missing: 0 / 1200
tabulation: Freq. Numeric Label
382 1 low
325 2 medium
493 3 high
Before we run this analysis using logistic regression, let us look at a crosstab of hiqual by cred.
tab hiqual cred, all
Hi Quality |
School, Hi | Full Credent Teachers, Lo Med Hi
vs Not | low medium high | Total
-----------+---------------------------------+----------
not high | 351 218 240 | 809
high | 31 107 253 | 391
-----------+---------------------------------+----------
Total | 382 325 493 | 1,200
Pearson chi2(2) = 182.9062 Pr = 0.000
likelihood-ratio chi2(2) = 204.7688 Pr = 0.000
Cram r's V = 0.3904
gamma = 0.6398 ASE = 0.033
Kendall's tau-b = 0.3663 ASE = 0.023
Looking at the Pearson Chi Square value (182.9), the results suggest that the quality of the school (hiqual) is not independent of the credential status of the teachers (cred). But such a way of looking at these results is very limiting. Instead, lets look at this using a regression framework. Lets start by pretending for the moment that our outcome variable is not a 0/1 variable and that it is appropriate to use in a regular OLS analysis. Below we show how we could include the variable cred as a predictor and hiqual as an outcome variable in an OLS regression. We use the xi command with i.cred to break cred into two dummy variables. The variable _Icred_2 is 1 if cred is equal to 2, and zero otherwise. The variable _Icred_3 is one if cred is equal to 3 and 0 otherwise.
xi: regress hiqual i.cred
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
Source | SS df MS Number of obs = 1200
-------------+------------------------------ F( 2, 1197) = 107.63
Model | 40.1782656 2 20.0891328 Prob > F = 0.0000
Residual | 223.420901 1197 .186650711 R-squared = 0.1524
-------------+------------------------------ Adj R-squared = 0.1510
Total | 263.599167 1199 .21984918 Root MSE = .43203
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | .2480789 .0326025 7.61 0.000 .1841145 .3120434
_Icred_3 | .4320328 .0294485 14.67 0.000 .3742563 .4898092
_cons | .0811518 .0221046 3.67 0.000 .0377837 .12452
------------------------------------------------------------------------------
We can use the adjust command to get the predicted values for the 3 levels of cred as shown below.
adjust, by(cred)
-------------------------------------------------------------------------------
Dependent variable: hiqual Command: regress
Variables left as is: _Icred_2, _Icred_3
-------------------------------------------------------------------------------
----------------------
Full |
Credent |
Teachers, |
Lo Med Hi | xb
----------+-----------
low | .081152
medium | .329231
high | .513185
----------------------
Key: xb = Linear Prediction
Note that the low credentialed schools are the omitted group. The coefficient for the constant corresponds to the predicted value for the low credentialed group. The coefficient for I_cred_2 represents the difference between the medium credentialed group and the omitted group (.329 – .081 = .248). Note that the coefficient for I_cred_3 represents the predicted value for group 3 (the high credentialed minus the omitted group (.513 – .081 = .432).
Seeing how you interpret the parameter estimates in OLS regression will help in the interpretation of the parameter estimates when using logistic regression. Now let’s run this as a logistic regression and see how to interpret the parameter estimates. As you see below, the syntax for running this as a logistic regression is much like that for an OLS regression, except that we substituted the logit command for the regress command. The results are shown using logistic regression coefficients where the coefficient represents the change in the log odds of hiqual equaling 1 for a one unit change in the predictor.
xi: logit hiqual i.cred
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -661.13514
Iteration 2: log likelihood = -655.23229
Iteration 3: log likelihood = -655.0422
Iteration 4: log likelihood = -655.04182
Logistic regression Number of obs = 1200
LR chi2(2) = 204.77
Prob > chi2 = 0.0000
Log likelihood = -655.04182 Pseudo R2 = 0.1352
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 1.715133 .2214491 7.75 0.000 1.281101 2.149165
_Icred_3 | 2.47955 .2079086 11.93 0.000 2.072056 2.887043
_cons | -2.426799 .1873679 -12.95 0.000 -2.794033 -2.059565
------------------------------------------------------------------------------
Some prefer to use odds ratios to help make the coefficients more interpretable. The odds ratio is simply the exponentiated version of the logistic regression coefficient. For example, exp(1.715) = 5.557 (shown below). After running the logit command from above, we can type logit , or and the results from the last logit command are shown, except using odds ratios.
logit, or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 5.557413 1.230684 7.75 0.000 3.6006 8.577693
_Icred_3 | 11.93589 2.481573 11.93 0.000 7.941136 17.94018
------------------------------------------------------------------------------
Let’s interpret these odds ratios. The odds ratio for _Icred_2 is the odds of a medium credentialed school being high quality divided by the odds of a low credentialed school being high quality. Likewise, The odds ratio for _Icred_3 is the odds of a high credentialed school being high quality divided by the odds of a low credentialed school being high quality.
Referring back to the crosstabulation of hiqual and cred, we can reproduce these odds ratios. First, using the frequencies from that crosstab, we can manually compute the odds of a school being high-quality school at each level of cred.
- Cred = Low. Odds or a school being high quality = (31 / 351) = .08831909
- Cred = Medium. Odds or a school being high quality = (107 / 218) = .49082569
- Cred = High. Odds or a school being high quality = (253 / 240) = 1.0541667
Now, we can see that the odds ratio for _Icred_2 is the odds of a medium credentialed school being high quality divided by the odds of a low credentialed , or (.49082569 / .08831909) = 5.5574134. Likewise, the odds ratio for _Icred_3 is the odds of a high credentialed school being high quality divided by the odds of a low credentialed school being high quality, or (1.0541667 / .08831909) = 11.935887.
The above technique works fine in a simple situation, but if we had additional predictors in the model it would not work as easily. Below we demonstrate the same idea but using the adjust command with the exp option to get the predicted odds of a school being high-quality school at each level of cred.
adjust, by(cred) exp
-------------------------------------------------------------------------------
Dependent variable: hiqual Command: logistic
Variables left as is: _Icred_2, _Icred_3
-------------------------------------------------------------------------------
----------------------
Full |
Credent |
Teachers, |
Lo Med Hi | exp(xb)
----------+-----------
low | .088319
medium | .490826
high | 1.05417
----------------------
Key: exp(xb) = exp(xb)
The odds ratio for _Icred_2 should be the odds of a medium credentialed school being high quality (.490) divided by the odds of a low credentialed school being high quality (.088). Indeed, we see this is correct. This means that we estimate that the odds of a medium credentialed being high quality (odds = .490) is about 5.6 times that of a low credentialed school being high quality (odds = .088).
display .490 / .088
5.5681818
Likewise, the odds ratio for _Icred_3 should be the odds of a high credentialed school being high quality (1.05) divided by the odds of a low credentialed school being high quality (.088). Indeed, we see this is correct as well. The odds of a high credentialed school being high quality (which is 1.05) is about 11.9 times as high as the odds of a low credentialed school being high quality (which is 0.088).
display 1.05 / .088
11.931818
If this were a linear model (e.g. a regression with two dummies, or an ANOVA), we might be interested in the overall effect of cred. We can test the overall effect of cred in one of two ways. First, we could use the test command as illustrated below. This produces a Wald Test. Based on the results of this command, we would conclude that the overall effect of cred is significant.
test _Icred_2 _Icred_3
( 1) _Icred_2 = 0.0
( 2) _Icred_3 = 0.0
chi2( 2) = 146.58
Prob > chi2 = 0.0000
Instead, you might wish to use a likelihood ratio test, illustrated below. We first run the model with all of the predictors, i.e. the full model, and then use the estimates store command to save the results naming the results full (you can pick any name you like).
xi: logit hiqual i.cred
(some output omitted)
Logistic regression Number of obs = 1200
LR chi2(2) = 204.77
Prob > chi2 = 0.0000
Log likelihood = -655.04182 Pseudo R2 = 0.1352
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 1.715133 .2214491 7.75 0.000 1.281101 2.149165
_Icred_3 | 2.47955 .2079086 11.93 0.000 2.072056 2.887043
_cons | -2.426799 .1873679 -12.95 0.000 -2.794033 -2.059565
------------------------------------------------------------------------------
estimates store full
Next, we run the model omitting the variable(s) we wish to test, in this case, omitting i.cred.
xi: logit hiqual
(some output omitted)
Logistic regression Number of obs = 1200
LR chi2(0) = -0.00
Prob > chi2 = .
Log likelihood = -757.42622 Pseudo R2 = -0.0000
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | -.7270914 .0615925 -11.80 0.000 -.8478105 -.6063722
------------------------------------------------------------------------------
We can then use the lrtest command to compare the current model (specified as a period) to the model we named full.
lrtest . full
Likelihood-ratio test LR chi2(2) = 204.77 (Assumption: . nested in full) Prob > chi2 = 0.0000
This test is also clearly significant. If you look back to the crosstab output of hiqual and cred you will see a line that reads
likelihood-ratio chi2(2) = 204.7688 Pr = 0.000
which, interestingly enough, matches the likelihood ratio test shown above. Both of these tests use a likelihood ratio method for testing the overall association between cred and hiqual.
2.2 Two categorical predictors
2.2.1 A 2 by 2 Layout with Only Main Effects
Now let’s look at an analysis that involves 2 categorical predictors. We have created a variable called cred_hl which is a dummy variable that is 1 if the school has a high percentage of teachers with full credentials (high credentialed), and 0 if the school has a low percentage of teachers with full credentials (low credentialed). (Note that the medium group has been omitted. This is not a customary thing to do, but this will be useful to us later.) Likewise, we have created a variable called pared_hl which is a binary variable that is coded 1 if the parents education is high (which we will call high parent education, and 0 if the parents education is low (which we will call low parent education. (Again, note that the medium group has been omitted.) The model below looks at the effects of teacher’s credentials and parents education on whether the school is a high quality school, but does not include an interaction term.
logit hiqual cred_hl pared_hl
Iteration 0: log likelihood = -369.63859
Iteration 1: log likelihood = -295.88905
Iteration 2: log likelihood = -291.08927
Iteration 3: log likelihood = -290.89287
Iteration 4: log likelihood = -290.89221
Logistic regression Number of obs = 580
LR chi2(2) = 157.49
Prob > chi2 = 0.0000
Log likelihood = -290.89221 Pseudo R2 = 0.2130
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 2.732386 .2705797 10.10 0.000 2.20206 3.262712
pared_hl | -.1699762 .2084613 -0.82 0.415 -.5785529 .2386005
_cons | -2.470522 .2463809 -10.03 0.000 -2.953419 -1.987624
------------------------------------------------------------------------------
We then use the logit , or command to obtain odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 15.36951 4.158678 10.10 0.000 9.04362 26.12029
pared_hl | .8436849 .1758757 -0.82 0.415 .5607092 1.269471
------------------------------------------------------------------------------
To help interpret the odds ratios for cred_hl, let’s look at the predicted odds broken down by cred_hl and pared_hl using the adjust command.
adjust, by(cred_hl pared_hl) exp
--------------------------------------------------------------------------------
Dependent variable: hiqual Command: logistic
--------------------------------------------------------------------------------
----------------------------
Full | Parents
Credent | Education, Hi vs
Teachers, | Lo
Hi vs Lo | low high
----------+-----------------
low | .084541 .071326
high | 1.29935 1.09624
----------------------------
Key: exp(xb)
For example, the odds ratio for pared_hl is the odds of a school being high quality for high parent education schools divided by the odds of a school being high quality for low parent education schools.
display 1.09624 / 1.29935
.84368338
Likewise, the odds ratio for cred_hl is the odds of being a high quality school for high credentialed schools divided by the odds of being high quality for low credentialed schools, as illustrated below.
display 1.299/.0845
15.372781
Note that the above example used the odds for low parent education schools. Note that we get the same results if we use the odds for high parent education schools, as illustrated below.
display 1.09624 / .071326
15.369431
The above results indicate that the odds of being a high quality school for high credentialed schools is about 15.3 times as high as the odds of low credentialed schools being high quality.
Because we did not include an interaction in this model, it assumes that the impact of credentials is the same regardless of the level of education of the parents. As we saw above, the odds ratio comparing high versus low credentialed schools was the same (15.3) for schools with low parent education and schools with high parent education. Let’s look at how reasonable this assumption is by comparing the predicted probabilities of the schools being high quality for the 4 cells with the actual probabilities of the schools being high quality. Below we see the predicted probabilities.
adjust, by(cred_hl pared_hl) pr
-------------------------------------------------------------------------
Dependent variable: hiqual Command: logistic
-------------------------------------------------------------------------
----------------------------
Full | Parents
Credent | Education, Hi vs
Teachers, | Lo
Hi vs Lo | low high
----------+-----------------
low | .077951 .066577
high | .565095 .522956
----------------------------
Key: Probability
Below we see the actual probabilities of the schools being high quality broken down by the 4 cells.
table cred_hl pared_hl, contents(mean hiqual)
------------------------------
Full |
Credent | Parents Education,
Teachers, | Hi vs Lo
Hi vs Lo | low high
----------+-------------------
low | .0523256 .1190476
high | .5984849 .5
------------------------------
Based on these probabilities, let’s look at the odds ratio for cred when parents education is low. When parents education is low, the observed odds ratio is about 27.
p2 / (1 - p2) odds2 0.60 / (1 - 0.60) 1.490
or = --------------- = ------- = ------------------- = ------- = 27.000
p1 / (1 - p1) odds1 0.05 / (1 - 0.05) 0.055
Let’s compare the above result to the odds ratio for cred when parents education is high. When parents education is high the observed odds ratio for cred is about 7.4.
p2 / (1 - p2) odds2 0.50 / (1 - 0.50) 1.000
or = --------------- = ------- = ------------------- = ------- = 7.403
p1 / (1 - p1) odds1 0.12 / (1 - 0.12) 0.135
As you see, when we included just main effects in the model, the overall odds ratio for cred was 15.3, but when parents education is low the odds ratio is about 27 and when parents education is high the odds ratio is 7.4. These odds ratios seem considerably different, yet because we only included main effects the model, the model just estimates one overall odds ratio for cred. However, if we include an interaction term in the model, then the model will estimate these odds ratios separately.
2.2.2 A 2 by 2 Layout with Main Effects and Interaction
We will create an interaction term by multiplying cred_hl by pared_hl to create cred_ed.
generate cred_ed = cred_hl*pared_hl
(620 missing values generated)
We can then include this interaction term in the analysis.
logit hiqual cred_hl pared_hl cred_ed
Iteration 0: log likelihood = -369.63859
Iteration 1: log likelihood = -293.82815
Iteration 2: log likelihood = -288.35139
Iteration 3: log likelihood = -287.98135
Iteration 4: log likelihood = -287.97695
Iteration 5: log likelihood = -287.97695
Logistic regression Number of obs = 580
LR chi2(3) = 163.32
Prob > chi2 = 0.0000
Log likelihood = -287.97695 Pseudo R2 = 0.2209
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 3.295682 .38571 8.54 0.000 2.539704 4.051659
pared_hl | .8950456 .4803744 1.86 0.062 -.0464709 1.836562
cred_ed | -1.294202 .5320893 -2.43 0.015 -2.337078 -.2513256
_cons | -2.896526 .3424121 -8.46 0.000 -3.567641 -2.22541
------------------------------------------------------------------------------
The significant interaction suggest that the effect of cred_hl depends on the level of pared_hl (and likewise, effect of pared_hl depends on the level of cred_hl). We explore this further using the odds ratio metric below.
logit, or
Logit estimates Number of obs = 580
LR chi2(3) = 163.32
Prob > chi2 = 0.0000
Log likelihood = -287.97695 Pseudo R2 = 0.2209
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 26.99581 10.41255 8.54 0.000 12.67592 57.49278
pared_hl | 2.447447 1.175691 1.86 0.062 .9545923 6.274929
cred_ed | .2741166 .1458545 -2.43 0.015 .0966096 .7777691
------------------------------------------------------------------------------
We can use the adjust command to get the predicted odds broken down by the 4 groups.
adjust, by(cred_hl pared_hl) exp
---------------------------------------------------------------------------------
Dependent variable: hiqual Command: logistic
Variable left as is: cred_ed
---------------------------------------------------------------------------------
----------------------------
Full | Parents
Credent | Education, Hi vs
Teachers, | Lo
Hi vs Lo | low high
----------+-----------------
low | .055215 .135135
high | 1.49057 1
----------------------------
Key: exp(xb)
The odds ratio for pared_hl is the odds of a high parent education school being high quality divided by the odds of a low parent education school being high quality, for low credentialed schools (because low credentialed is coded as 0).
display.135135 / .055215
2.4474328
Likewise, the odds ratio for cred_hl is the odds of a high credentialed school being high quality divided by the odds of a low credentialed school being high quality, for low parent education schools (because low parent education is coded 0).
display 1.49057 / .055215
26.995744
We can see the meaning of the interaction by comparing the odds ratio for the effect of cred_hl for high parent education schools and for low parent education schools. When parent education is low, we have seen that the odds ratio for cred_hl is 26.99 (see output from the logistic command above). When parent education is high, the odds ratio for cred_hl is shown below.
display 1 / .1351
7.4019245
The odds ratio for the interaction is actually the ratio of two odds ratios. Focusing on the effect of cred_hl, the interaction can be thought of as the odds ratio for cred_hl when parents education is high (i.e. 7.4) divided by the odds ratio for cred_hl when parents education is low (i.e., 26.99). As you see below, the ratio of these two odds ratios is the interaction.
display 7.4 / 26.99
.27417562
Here is another way to look at this. We know the odds ratio for cred_hl is 26.99 for low parent education schools. If we multiply this by the interaction term (by .274) we get the odds ratio for the high parent education schools. As we see below, 26.99 * .274 yields the odds ratio (with a touch of rounding error) for high parent education schools.
display 26.99 * .274
7.39526
The impact of cred_hl depends on the level of education of the parents. When parent education is low, the impact of cred_hl is much higher than when parent education is high. In particular, when parent education is low, the odds of high credentialed schools being high quality are 27 times than the odds of low credentialed schools being high quality. By contrast, the odds ratio for cred_hl for schools with high parent education is .274 times the low parent education schools. For the high parent education schools, the odds of high credentialed schools being high quality is about 7.4 times that of the low credentialed schools.
2.2.3 A 2 by 3 Layout with Only Main Effects
We can extend the above analysis into a 3 by 2 design by looking at all 3 levels of parent education (low, medium and high) by using the variable pared instead of pared_hl. We will use this example to illustrate how to run and interpret the results of such an analysis. As above, we will start with a model which includes just main effects, and then will move on to a model which includes both main effects and an interaction.
We can look at a model which includes cred_hl and pared as predictors as shown below. We use the xi prefix with i.pared to break parent education into two dummy variables _Ipared_2 which is 1 if parent education is medium, 0 otherwise; and _Ipared_3 which is 1 if parent education is high, 0 otherwise.
xi: logit hiqual cred_hl i.pared
i.pared _Ipared_1-3 (naturally coded; _Ipared_1 omitted)
Iteration 0: log likelihood = -551.48395
Iteration 1: log likelihood = -454.38244
Iteration 2: log likelihood = -448.38948
Iteration 3: log likelihood = -448.19569
Iteration 4: log likelihood = -448.1953
Logistic regression Number of obs = 875
LR chi2(3) = 206.58
Prob > chi2 = 0.0000
Log likelihood = -448.1953 Pseudo R2 = 0.1873
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 2.511303 .2123631 11.83 0.000 2.095079 2.927527
_Ipared_2 | -.2761497 .205192 -1.35 0.178 -.6783186 .1260191
_Ipared_3 | -.1296273 .2035595 -0.64 0.524 -.5285967 .269342
_cons | -2.313248 .2083214 -11.10 0.000 -2.72155 -1.904945
------------------------------------------------------------------------------
And below we shown the results using odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 12.32098 2.616521 11.83 0.000 8.126085 18.68138
_Ipared_2 | .7586993 .155679 -1.35 0.178 .5074695 1.134304
_Ipared_3 | .8784227 .1788113 -0.64 0.524 .5894316 1.309103
------------------------------------------------------------------------------
These results indicate that cred_hl is significant, and that the odds of a high credentialed school being high quality is about 12.3 times that of low credentialed schools. Neither of the terms for parent education ( _Ipared_2 or _Ipared_3) are significant. However, let’s test the joint influence of these two variables using the test command.
test _Ipared_2 _Ipared_3
( 1) _Ipared_2 = 0.0
( 2) _Ipared_3 = 0.0
chi2( 2) = 1.82
Prob > chi2 = 0.4020
As we would have expected based on the individual tests, the overall effect of parents education is not significant.
Let’s now look at the interpretation of the odds ratios. First, let’s get the predicted odds for the 6 cells of this design using the adjust command.
adjust, by(cred_hl pared) exp
-------------------------------------------------------------------------------
Dependent variable: hiqual Command: logistic
Variables left as is: _Ipared_2, _Ipared_3
-------------------------------------------------------------------------------
-------------------------------------
Full |
Credent | Parents Education, Lo Med
Teachers, | Hi
Hi vs Lo | low medium high
----------+--------------------------
low | .098939 .075065 .086911
high | 1.21903 .924877 1.07082
-------------------------------------
Key: exp(xb)
As you would expect, the odds ratio for cred_hl is the odds that a high credentialed school will be high quality divided by the odds that a low credentialed school would be high quality. We illustrate this below.
display 1.219 / .0989
12.325581
The above odds ratio was computed when parents education is low, but we get the same result if we use medium or high parent education. This is because this model did not contain an interaction between pared and cred_hl.
display .924 / .075
12.32
display 1.07 / .0869
12.313003
The odds ratio for _Ipared_2 is the odds that a medium parent education school will be high quality divided by the odds that a low parent education school will be high quality, for example.
display .075 / .0989
.75834176
The odds ratio for _Ipared_3 is the odds that a high parent education school will be high quality divided by the odds that a low parent education school will be high quality, for example.
display .0869 / .0989
.87866532
These last two effects were computed when credentials was low. If we had computed them when credentials was high, we would have gotten the same result (you can try it for yourself).
This model includes only main effects, so it assumes that the effect of cred_hl are the same across the levels of parent education. We can look at the probabilities of being a high quality school by cred_hl and by parent education.
table cred_hl pared, contents(mean hiqual)
----------------------------------------
Full |
Credent |
Teachers, | Parents Education, Lo Med Hi
Hi vs Lo | low medium high
----------+-----------------------------
low | .0523256 .0952381 .1190476
high | .5984849 .4615385 .5
----------------------------------------
Let’s now look at the odds ratio for cred_hl at each level of parent education. This model with main effects is assuming that these odds ratios will be roughly the same, but we can look at them and see if this appears reasonable.
Odds ratio for cred_hl when parent education is low
p2 / (1 - p2) odds2 0.60 / (1 - 0.60) 1.488
or = --------------- = ------- = ------------------- = ------- = 27.119
p1 / (1 - p1) odds1 0.05 / (1 - 0.05) 0.055
Odds ratio for cred_hl when parent education is medium
p2 / (1 - p2) odds2 0.46 / (1 - 0.46) 0.855
or = --------------- = ------- = ------------------- = ------- = 8.148
p1 / (1 - p1) odds1 0.10 / (1 - 0.10) 0.105
Odds ratio for cred_hl when parent education is high
p2 / (1 - p2) odds2 0.50 / (1 - 0.50) 1.000
or = --------------- = ------- = ------------------- = ------- = 7.403
p1 / (1 - p1) odds1 0.12 / (1 - 0.12) 0.135
It seems that the odds ratio for cred_hl is much higher when parent education is low as compared to parents with medium and high levels of education. By including an interaction term in the model (as shown below) we can capture these differences in cred_hl across levels of parent education.
2.2.4 A 2 by 3 Layout with Main Effects and Interaction
The analysis above only included main effects of parent education and the credentials of the teachers, but did not include an interaction of these two variables. The analysis below includes this interaction.
xi: logit hiqual i.cred_hl*i.pared
i.cred_hl _Icred_hl_0-1 (naturally coded; _Icred_hl_0 omitted)
i.pared _Ipared_1-3 (naturally coded; _Ipared_1 omitted)
i.cr~hl*i.pared _IcreXpar_#_# (coded as above)
Iteration 0: log likelihood = -551.48395
Iteration 1: log likelihood = -451.33208
Iteration 2: log likelihood = -444.62299
Iteration 3: log likelihood = -444.24823
Iteration 4: log likelihood = -444.24435
Iteration 5: log likelihood = -444.24435
Logistic regression Number of obs = 875
LR chi2(5) = 214.48
Prob > chi2 = 0.0000
Log likelihood = -444.24435 Pseudo R2 = 0.1945
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | 3.295682 .38571 8.54 0.000 2.539704 4.051659
_Ipared_2 | .6452338 .4575493 1.41 0.158 -.2515463 1.542014
_Ipared_3 | .8950456 .4803744 1.86 0.062 -.0464709 1.836562
_IcreXpar_~2 | -1.19854 .5144774 -2.33 0.020 -2.206898 -.1901832
_IcreXpar_~3 | -1.294202 .5320893 -2.43 0.015 -2.337078 -.2513256
_cons | -2.896526 .3424121 -8.46 0.000 -3.567641 -2.22541
------------------------------------------------------------------------------
And here are the odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | 26.99581 10.41255 8.54 0.000 12.67592 57.49278
_Ipared_2 | 1.906433 .8722869 1.41 0.158 .7775975 4.673994
_Ipared_3 | 2.447447 1.175691 1.86 0.062 .9545923 6.274929
_IcreXpar_~2 | .3016341 .155184 -2.33 0.020 .1100415 .8268076
_IcreXpar_~3 | .2741166 .1458545 -2.43 0.015 .0966096 .7777691
------------------------------------------------------------------------------
Let’s now look at the interpretation of the odds ratios for this analysis. Previously we have used the adjust command to obtain predicted odds. This time, let’s do this a bit different (just for some variety, and to try and see this from a different angle). This time let’s compute the predicted probability of hiqual being 1 using the predict command with the pr option (the default).
predict predp , pr (325 missing values generated)
Below the table command is used to show the predicted probability of hiqual being 1 when broken down by cred_hl and pared. You might think you are having double vision, but note that the top line of the table shows the minimum value of predp and the second line shows the maximum value of predp, both of which are the same, showing that the predicted values are all identical within each cell (as they should be, since there are no other covariates in the model). We can then use these values to illustrate the meaning of the odds ratios from the above model.
table cred_hl pared, contents(min predp max predp)
----------------------------------------
Full |
Credent |
Teachers, | Parents Education, Lo Med Hi
Hi vs Lo | low medium high
----------+-----------------------------
low | .0523256 .0952381 .1190476
| .0523256 .0952381 .1190476
|
high | .5984849 .4615385 .5
| .5984849 .4615385 .5
----------------------------------------
The odds ratio for _Icred_hl_1 represents the odds ratio of hiqual being 1 for cred_hl when parent education is low (because this was the omitted group for pared). This is shown below, illustrating that when parent education is low, the odds of a high credentialed school being high quality is about 27 times that of a low credentialed school.
display ( .5984849 / (1 - .5984849)) / (.0523256 / (1 - .0523256)) 26.995803
The odds ratio for _Ipared_2 is the odds ratio formed by comparing schools with medium parent education with schools with low parent education for schools with low teacher credentials (because this is the reference group for cred_hl). We illustrate this below, which shows that when when teacher credentials are low, schools with medium parent education have an odds or being high quality that is about 1.9 times of schools with low parent education; however this effect is not statistically significant.
display ( .0952381 / ( 1 - .0952381)) / ( .0523256 / ( 1 - .0523256)) 1.9064321
The effect of _Ipared_3 is very similar to _Ipared_2, except that this compares the effect of high parent education schools with low parent education schools, that is,
display ( .1190476 / ( 1 - .1190476)) / ( .0523256 / ( 1 - .0523256)) 2.4474461
This effect is not statistically significant.
The variable _IcreXpar_~2 is an interaction term that crosses cred_hl with _Ipared_2. Because _Ipared_2 compares medium parent education schools with low parent education schools, the odds ratio for _IcreXpar_~2 is a comparison of the odds ratio for cred_hl for medium parent education schools as compared to low parent education schools. We can illustrate this below. The odds ratio for cred_hl for medium parent education schools is
display (.4615385 / (1 - .4615385 )) / ( .0952381 / (1 - .0952381)) 8.142858
and the odds ratio for cred_hl for low parent education schools is
display ( .5984849 / (1 - .5984849)) / (.0523256 / (1 - .0523256)) 26.995803
So the ratio of these odds is the coefficient for _IcreXpar_~2. In other words, the odds ratio for cred_hl when parent education is medium is about .3 (about 30%) of the size of the odds ratio for cred_hl when parent education is low.
display 8.146 / 26.9927
.3017853
If we invert this odds ratio (1 / .3017) we get about 3.31, so we could likewise say that the odds ratio for cred_hl for low parent education schools is about 3.3 times that for medium parent education schools. This effect is statistically significant.
The interpretation for _IcreXpar_~3 is similar to _IcreXpar_~2, except that it compares the odds ratios for cred_hl for the high parent education schools with the low parent education schools.
We should emphasize that when you have interaction terms, it is important to be very careful when interpreting any of the terms involved in the interaction. For example, in the above model you might be tempted to interpret _Ipared_2 as some kind of overall comparison of medium educated to low educated parents, as you normally would. However, because this term was part of an interaction, the interpretation is different. It is not the overall effect of high versus low education, but it is this effect when the other terms in the interaction are at the reference category (i.e., when cred_hl was low). Likewise, the effect of _Icred_hl_1 is not the overall effect of cred_hl, but it is the effect of cred_hl when pared is at the reference category (i.e., when pared is low).
2.3 Categorical and Continuous Predictors
All of the prior examples in this chapter have used only categorical predictors. In chapter 1, we saw models which included categorical predictors, continuous predictors, and models that included categorical and continuous predictors. This section will focus on models that include both continuous and categorical predictors, as well as models that include interactions between a continuous and categorical predictor.
2.3.1 A Continuous and a Two Level Categorical Predictor
Let’s first consider a model with one categorical predictor (with 2 levels) and one continuous predictor. The model below predicts hiqual from cred_hl and meals (the percentage of students receiving free meals).
logit hiqual cred_hl meals
Iteration 0: log likelihood = -551.48395
Iteration 1: log likelihood = -272.58457
Iteration 2: log likelihood = -222.88248
Iteration 3: log likelihood = -207.71944
Iteration 4: log likelihood = -205.32492
Iteration 5: log likelihood = -205.2436
Iteration 6: log likelihood = -205.24348
Logistic regression Number of obs = 875
LR chi2(2) = 692.48
Prob > chi2 = 0.0000
Log likelihood = -205.24348 Pseudo R2 = 0.6278
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | .9843681 .3097759 3.18 0.001 .3772184 1.591518
meals | -.1060442 .0078372 -13.53 0.000 -.1214048 -.0906836
_cons | 2.711355 .3792046 7.15 0.000 1.968128 3.454582
------------------------------------------------------------------------------
And here are the results expressed using odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
cred_hl | 2.67612 .8289977 3.18 0.001 1.458223 4.911198
meals | .8993849 .0070486 -13.53 0.000 .8856753 .9133066
------------------------------------------------------------------------------
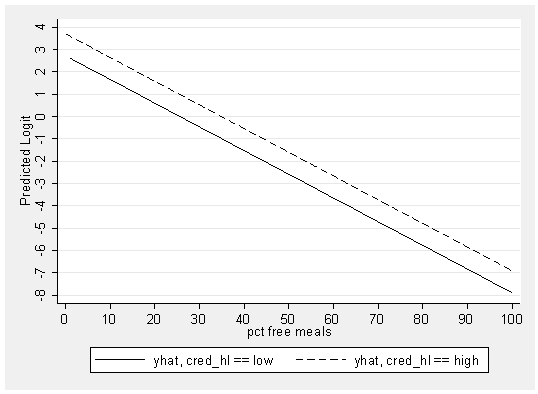
Let’s now make a graph of the predicted values showing the predicted logit by meals.
predict yhat, xb (325 missing values generated)
We would like to make a graph which shows the predicted value for low credentialed and high credentialed using separate lines for each type of school. To do this, we need to make a separate variable that has the predicted value for the low credentialed and high credentialed schools. We can use the separate command below to take the predicted value (yhat) and make separate variables for each level of cred_hl (i.e., making yhat0 for the low credentialed schools, and yhat1 for the high credentialed schools).
separate yhat, by(cred_hl)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- yhat0 float %9.0g yhat, cred_hl == low yhat1 float %9.0g yhat, cred_hl == high
We can now show a graph of the predicted values using separate lines for the two types of schools.
graph twoway line yhat0 yhat1 meals, xlabel(0 10 to 100) /// ylabel(-8 -7 to 4) ytitle(Predicted Logit) sort scheme(s2mono)
Let’s look at the coefficients for this model, and relate those coefficients to the predicted logits in the graph above. The coefficient for meals is -.106, which reflects the slope of the lines in the above graph. The coefficient for cred_hl represents the difference in the heights of the two lines (with the line for high credentialed) schools being .984 units higher than the line for the low credentialed schools. (Note that the units in this graph are the log odds of a school being high quality.) Rather than focusing on the particular meaning of these coefficients, we wish to emphasize that the predicted logits in this model for the two groups form 2 parallel lines. The lines are parallel because the outcome is in the form of logits and the model only has main effects. We will soon look at a model which has an interaction of meals and cred_hl, which would then permit the lines to be non-parallel.
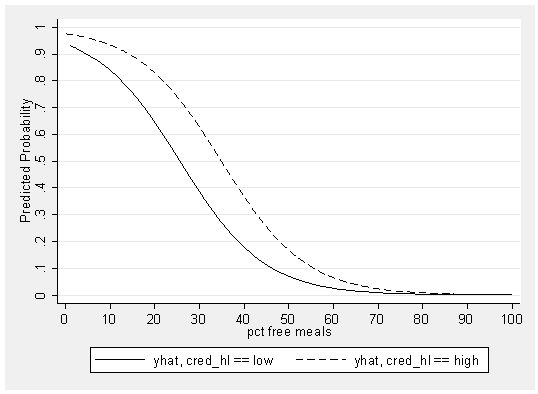
We can view the same type of graph, except showing the predicted probability (instead of the predicted logit). Rather than making new variables to contain the predicted values, let’s use the same variable names, yhat yhat0 and yhat1, so let’s drop these variables from the data file so we may use these variable names again.
drop yhat yhat0 yhat1
Now let’s generate the predicted value, but this time in terms of the predicted probability, using the pr option.
predict yhat, pr
(325 missing values generated)
And let’s separate these into two different variables based on cred_hl.
separate yhat, by(cred_hl)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- yhat0 float %9.0g yhat, cred_hl == low yhat1 float %9.0g yhat, cred_hl == high
And below we see the graph showing the relationship between meals and the predicted probability of being a high quality school, with separate lines for high credentialed and low credentialed schools. Although these lines do not look exactly parallel, they are parallel in that they both reflect the same odds ratio. The odds ratio for meals is .899, so for every unit increase in meals, the odds of a school being high quality changes by .899. This is the same for the high credentialed and low credentialed schools.
graph twoway line yhat0 yhat1 meals, xlabel(0 10 to 100) /// ylabel(0 .1 to 1) ytitle(Predicted Probability) sort scheme(s2mono)
2.3.2 A Continuous and a Two Level Categorical Predictor with Interaction
Now let’s include an interaction between cred_hl and meals which allows the relationship between meals and hiqual to be different for the high credentialed and low credentialed schools, i.e., allowing the lines of the predicted values to be non-parallel.
We will use the xi command in this model to make it easy to create the interaction of cred_hl and meals.
xi: logit hiqual i.cred_hl*meals
i.cred_hl _Icred_hl_0-1 (naturally coded; _Icred_hl_0 omitted)
i.cred_hl*meals _IcreXmeals_# (coded as above)
Iteration 0: log likelihood = -551.48395
Iteration 1: log likelihood = -255.68833
Iteration 2: log likelihood = -213.88872
Iteration 3: log likelihood = -204.10454
Iteration 4: log likelihood = -202.74095
Iteration 5: log likelihood = -202.666
Iteration 6: log likelihood = -202.66558
Logistic regression Number of obs = 875
LR chi2(3) = 697.64
Prob > chi2 = 0.0000
Log likelihood = -202.66558 Pseudo R2 = 0.6325
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | 2.22788 .6102254 3.65 0.000 1.031861 3.4239
meals | -.0817427 .0114861 -7.12 0.000 -.1042552 -.0592303
_IcreXmeal~1 | -.0364404 .0153391 -2.38 0.018 -.0665045 -.0063763
_cons | 1.860882 .4916155 3.79 0.000 .8973332 2.824431
------------------------------------------------------------------------------
And here are the results expressed as odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | 9.280175 5.662998 3.65 0.000 2.806282 30.68887
meals | .921509 .0105846 -7.12 0.000 .9009954 .9424897
_IcreXmeal~1 | .9642156 .0147902 -2.38 0.018 .9356587 .993644
------------------------------------------------------------------------------
Note that the interaction term is significant.
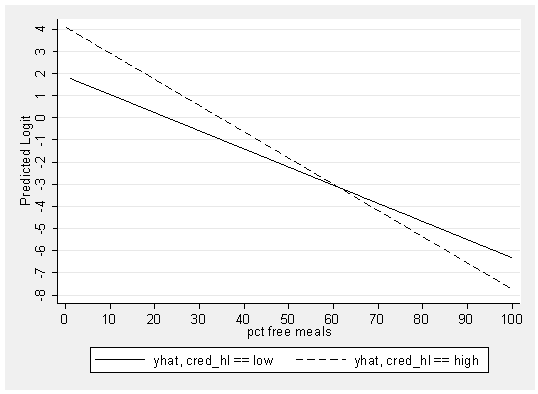
Let’s now make a graph of the predicted values showing the predicted logit by meals. As we have done before, we will use the drop command to drop the variables we have used before.
drop yhat yhat0 yhat1
We use the predict command to get the predicted logit.
predict yhat, xb
(325 missing values generated)
And we use the separate command to make separate variables for the high credentialed and low credentialed schools.
separate yhat, by(cred_hl)
storage display value variable name type format label variable label ------------------------------------------------------------------------------- yhat0 float %9.0g yhat, cred_hl == low yhat1 float %9.0g yhat, cred_hl == high
Below we graph the relationship between meals and the predicted logit for a school being high quality.
graph twoway line yhat0 yhat1 meals, xlabel(0 10 to 100) /// ylabel(-8 -7 to 4) ytitle(Predicted Logit) sort scheme(s2mono)
You can clearly see that the lines of the predicted logits for the two groups are not parallel. This makes sense since the variable representing the interaction, _IcreXmeal~1, was significant. In fact, as you look at the graph above you can see that it looks like there are really two regression lines, one for the low credentialed group and another for the high credentialed group. To make this explicit, let’s re-write the logit model from the results above as two separate equations, one for each group.
low credentialed group
logit(hiqual) = 1.86 + -0.0817*meals
high credentialed group
logit(hiqual) = (1.86 + 2.22) + (-0.0817 + -.036)*meals
or more simply
logit(hiqual) = 4.088 + -.118*meals
Note that the low credentialed group has an intercept of 1.86 and a slope of -.08, while the high credentialed group has an intercept of 4.088 and a slope of -.118.
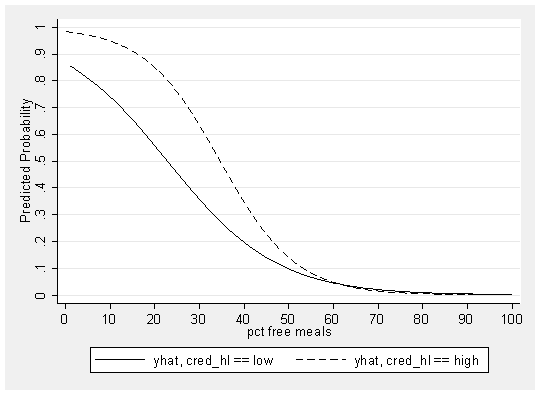
Let’s look at the same graph except substituting the predicted probabilities for the predicted logits by using the pr option on the predict command when we compute the predicted probabilities.
drop yhat yhat0 yhat1 predict yhat, pr separate yhat, by(cred_hl) graph twoway line yhat0 yhat1 meals, xlabel(0 10 to 100) /// ylabel(0 .1 to 1) ytitle(Predicted Probability) sort scheme(s2mono)
You can see that the differences in the shape of these two lines as well. Because we included an interaction term, the odds ratio for the high credentialed schools is different from the odds ratio for the low credentialed schools. In fact, if we look at the results of the logistic command, we can see that the odds ratio for the low credentialed schools (the reference group) is .921. The odds ratio for the high credentialed schools is .921 * .964 or .887. Note that we took the odds ratio for the reference group and then multiplied that by the interaction term, and that yielded the odds ratio for the high credentialed schools (in contrast to when we were dealing with predicted logits we added these terms together, but when we are dealing with predicted probabilities we multiply these together). Another way of thinking about this is that the interaction term is the odds ratio for the high credentialed schools divided by the odds ratio for the low credentialed schools. In this case, the odds ratio for the high credentialed schools is .964 of that of the low credentialed schools.
The odds ratio for _Icred_hl_1 is a bit tricky to interpret because it is part of the interaction term. You might be temped to interpret this as a kind of overall effect of cred_hl; however, this is not the case. The odds ratio for _Icred_hl_1 is the odds ratio when meals is 0. Looking at the graph, think of forming the odds ratio for cred_hl based on the predicted probabilities when meals is 0 (i.e., about .98 versus .84). Based on this rough estimate we can compute the odds ratio for cred_hl when meals is 0 and compare that to the coefficient for _Icred_hl_1.
p2 / (1 - p2) odds2 0.98 / (1 - 0.98) 49.000
or = --------------- = ------- = ------------------- = ------- = 9.333
p1 / (1 - p1) odds1 0.84 / (1 - 0.84) 5.250
Indeed, the coefficient corresponds to what we see in the graph. However, very few schools have a value of meals being 0, so this may not be a very useful value for this coefficient. Instead, we can center the variable meals to have a mean of 0 by subtracting the mean, and then this term would represent the odds ratio for cred_hl when meals is at the overall average.
First, below we center the variable meals creating a new variable called mealcent.
summarize meals generate mealcent=meals-r(mean) summ mealcent
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
mealcent | 1200 -4.77e-07 31.23653 -52.15 47.85
Next, we include mealcent as the continuous variable in our model.
xi: logit hiqual i.cred_hl*mealcent
i.cred_hl _Icred_hl_0-1 (naturally coded; _Icred_hl_0 omitted)
i.cre~hl*meal~t _IcreXmealc_# (coded as above)
Iteration 0: log likelihood = -551.48395
Iteration 1: log likelihood = -255.68833
Iteration 2: log likelihood = -213.88872
Iteration 3: log likelihood = -204.10454
Iteration 4: log likelihood = -202.74095
Iteration 5: log likelihood = -202.666
Iteration 6: log likelihood = -202.66558
Iteration 7: log likelihood = -202.66558
Logistic regression Number of obs = 875
LR chi2(3) = 697.64
Prob > chi2 = 0.0000
Log likelihood = -202.66558 Pseudo R2 = 0.6325
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | .3275149 .3919626 0.84 0.403 -.4407176 1.095747
mealcent | -.0817427 .0114865 -7.12 0.000 -.1042558 -.0592296
_IcreXmeal~1 | -.0364404 .0153394 -2.38 0.018 -.066505 -.0063758
_cons | -2.402002 .3009785 -7.98 0.000 -2.991909 -1.812095
------------------------------------------------------------------------------
And here are the results as odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_hl_1 | 1.387516 .5438542 0.84 0.403 .6435744 2.991418
mealcent | .921509 .0105849 -7.12 0.000 .9009948 .9424903
_IcreXmeal~1 | .9642156 .0147904 -2.38 0.018 .9356583 .9936445
------------------------------------------------------------------------------
Note that the only term that changed in the model was _Icred_hl_1 which now reflects the effect of cred_hl when meals is at the mean (about 52). Note that this effect is not significant. We can eyeball this value by computing the odds ratio for these two groups when meals is 52, which is about .09 versus .13 (see below). This eyeball value is about 1.5, which is close to the actual value (1.38).
p2 / (1 - p2) odds2 0.13 / (1 - 0.13) 0.149
or = --------------- = ------- = ------------------- = ------- = 1.511
p1 / (1 - p1) odds1 0.09 / (1 - 0.09) 0.099
Now let’s consider a model with a three level categorical predictor.
2.3.3 A Continuous and a Three Level Categorical Predictor
Let us extend this example further to include 3 categories for the variable cred, including schools with low, medium and high credentialed teachers. We start by looking at a model with just main effects (no interaction).
xi: logit hiqual i.cred mealcent
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -393.01669
Iteration 2: log likelihood = -328.35404
Iteration 3: log likelihood = -309.75082
Iteration 4: log likelihood = -307.17923
Iteration 5: log likelihood = -307.11337
Iteration 6: log likelihood = -307.11332
Logistic regression Number of obs = 1200
LR chi2(3) = 900.63
Prob > chi2 = 0.0000
Log likelihood = -307.11332 Pseudo R2 = 0.5945
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | .7536416 .3268903 2.31 0.021 .1129484 1.394335
_Icred_3 | .984952 .3089191 3.19 0.001 .3794817 1.590422
mealcent | -.1054114 .0065193 -16.17 0.000 -.118189 -.0926337
_cons | -2.806948 .3003886 -9.34 0.000 -3.395699 -2.218197
------------------------------------------------------------------------------
And here are the results as odds ratios.
logit , or
(some output omitted)
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 2.124723 .6945514 2.31 0.021 1.119574 4.032291
_Icred_3 | 2.677683 .8271875 3.19 0.001 1.461527 4.90582
mealcent | .8999542 .0058671 -16.17 0.000 .8885281 .9115273
------------------------------------------------------------------------------
First, let’s look at the odds ratios for cred_hl. The odds ratio for _Icred_2 compares the medium credentialed schools to the low credentialed schools (because the low credentialed schools are the reference group). This indicates that a medium credentialed school has an odds of being high quality that is 2.12 times that of the low credentialed schools. Likewise, the effect for _Icred_3 indicates that the odds of being high quality for high credentialed schools is 2.677 that of the low credentialed schools. Note that since we did not have an interaction term in the model, we can talk about these overall effects without needing to worry about other predictors in the model.
The effect of mealcent indicates that for every unit increase in mealcent, the odds of being a high quality school changes by a factor of .8999 (about .9). Because this model does not include an interaction term, this model provides a single estimate for the effect of mealcent for all 3 levels of cred. Below we can create and plot the predicted probabilities for the 3 levels of cred.
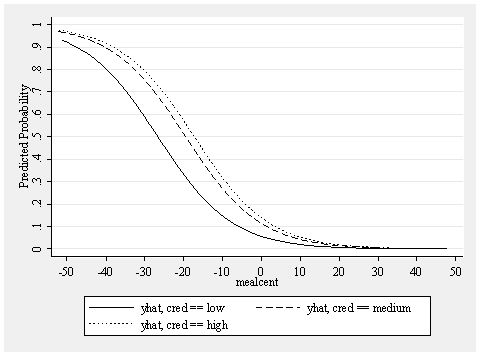
drop yhat yhat0 yhat1 predict yhat, pr separate yhat, by(cred) graph twoway line yhat1 yhat2 yhat3 mealcent, /// xlabel(-50 -40 to 50) ylabel(0 .1 to 1) ytitle(Predicted Probability) /// sort scheme(s2mono)
The above graph illustrates that as mealcent increases, the probability of being a high quality school decreases. We can see that the shape of this relationship is basically the same across the three levels of cred (because we have only included main effects in the model). Now let’s look at a model where we include interactions.
2.3.4 A Continuous and a Three Level Categorical Predictor with Interaction
This model is the same as the one we examined above, except that it includes an interaction of cred and mealcent.
xi: logit hiqual i.cred*mealcent
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred*mealcent _IcreXmealc_# (coded as above)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -375.90053
Iteration 2: log likelihood = -319.1446
Iteration 3: log likelihood = -306.19596
Iteration 4: log likelihood = -304.60216
Iteration 5: log likelihood = -304.52497
Iteration 6: log likelihood = -304.52455
Iteration 7: log likelihood = -304.52455
Logistic regression Number of obs = 1200
LR chi2(5) = 905.80
Prob > chi2 = 0.0000
Log likelihood = -304.52455 Pseudo R2 = 0.5979
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | .3751273 .4088819 0.92 0.359 -.4262664 1.176521
_Icred_3 | .3275149 .3919626 0.84 0.403 -.4407176 1.095747
mealcent | -.0817427 .0114865 -7.12 0.000 -.1042558 -.0592296
_IcreXmeal~2 | -.0222125 .0164334 -1.35 0.176 -.0544214 .0099964
_IcreXmeal~3 | -.0364404 .0153394 -2.38 0.018 -.066505 -.0063758
_cons | -2.402002 .3009785 -7.98 0.000 -2.991909 -1.812095
------------------------------------------------------------------------------
xi: logistic hiqual i.cred*mealcent
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred*mealcent _IcreXmealc_# (coded as above)
Logit estimates Number of obs = 1200
LR chi2(5) = 905.80
Prob > chi2 = 0.0000
Log likelihood = -304.52455 Pseudo R2 = 0.5979
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 1.455177 .5949954 0.92 0.359 .6529424 3.243072
_Icred_3 | 1.387516 .5438542 0.84 0.403 .6435744 2.991418
mealcent | .921509 .0105849 -7.12 0.000 .9009948 .9424903
_IcreXmeal~2 | .9780324 .0160724 -1.35 0.176 .9470329 1.010047
_IcreXmeal~3 | .9642156 .0147904 -2.38 0.018 .9356583 .9936445
------------------------------------------------------------------------------
We now must be much more careful in the interpretation of these results due to the interaction term. But first, let us make a graph of the predicted probabilities to help us picture the results as we interpret them.
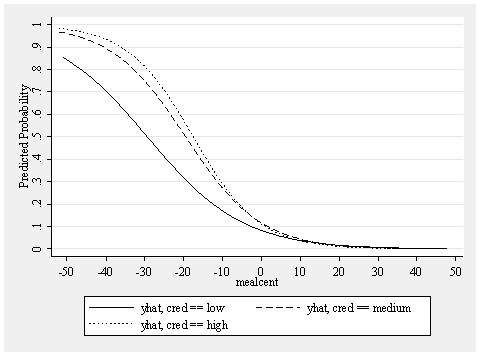
drop yhat yhat1 yhat2 yhat3 predict yhat, pr separate yhat, by(cred) graph twoway line yhat1 yhat2 yhat3 mealcent, /// xlabel(-50 -40 to 50) ylabel(0 .1 to 1) ytitle(Predicted Probability) /// sort scheme(s2mono)
This graph has 3 lines, but unlike the prior example these lines are not forced to be parallel. Each line has it own odds ratio determining its shape. As you can see, the dashed (cred=medium) and dotted (cred=high) schools have a similar shape, which is different from the solid line (cred=low). If we run the logistic regressions separately for each level of cred we can obtain the odds ratios for each of these 3 lines (the output has been edited to make it more brief).
sort cred
by cred: logit hiqual mealcent
-------------------------------------------------------------------------------
-> cred = low
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | -.0817427 .0114865 -7.12 0.000 -.1042558 -.0592297
_cons | -2.402002 .3009784 -7.98 0.000 -2.991909 -1.812095
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-> cred = medium
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | -.1039552 .0117517 -8.85 0.000 -.1269882 -.0809223
_cons | -2.026875 .2767457 -7.32 0.000 -2.569286 -1.484463
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-> cred = high
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | -.1181831 .010166 -11.63 0.000 -.1381081 -.0982581
_cons | -2.074487 .2510819 -8.26 0.000 -2.566598 -1.582376
------------------------------------------------------------------------------
sort cred by cred: logistic hiqual mealcent
-> cred = low
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | .921509 .0105849 -7.12 0.000 .9009948 .9424903
------------------------------------------------------------------------------
-> cred = medium
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | .9012656 .0105914 -8.85 0.000 .8807441 .9222654
------------------------------------------------------------------------------
-> cred = high
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | .8885333 .0090328 -11.63 0.000 .8710045 .9064149
------------------------------------------------------------------------------
These results indicate the odds ratio is .9215 when cred is low, .9012 when cred is medium, and .8885 when cred is high. Looking back at the graph, you see the dashed and dotted lines (where cred is medium and high) have the steepest descent, which corresponds to them having the smallest odds ratios. By contrast when cred is low, the effect of mealcent is not as strong, and hence the odds ratio for this group is closer to 1.
Let’s relate the odds ratios for the 3 groups to the odds ratios that we get from the original logistic regression analysis. First, note that the odds ratio for mealcent represents the odds ratio for the reference group on cred (i.e., when cred is low). Indeed, we see the odds ratio for mealcent is .921.
The odds ratio for _IcreXmeal~2 represents the odds ratio for mealcent for the medium credentialed schools divided by the odds ratio for the low credentialed schools, see below. If the odds ratios for these groups were identical, then this ratio would be 1. This result indicates that the odds ratio for medium credentialed schools is .978 of that for the low credentialed schools, but this is not a significant effect.
display .9012656 / .921509
.97803234
Likewise, the odds ratio for _IcreXmeal~3 represents the odds ratio for mealcent for the high credentialed schools divided by the odds ratio for the low credentialed schools, see below. The odds ratio for high credentialed schools is .964 of that for the low credentialed schools, and this is a significant effect.
display .8885333 / .921509
.96421554
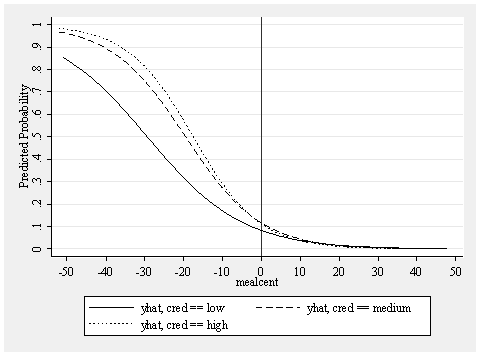
The odds ratios for _Icred_2 and _Icred_3 represent the effects of cred when mealcent is at 0 (which is the mean of meals). In particular, _Icred_2 tests the difference between low credentialed and medium credentialed schools when meals is at the mean. We have repeated the graph from above, but put a vertical line when mealcent is 0 to help you see what is being compared. This odds ratio for _Icred_2 compares the dashed line with the solid line at the vertical line (when mealcent is 0). Likewise, _Icred_3 tests the difference between low credentialed and high credentialed schools when meals is at the mean, so this compares the dotted line with the solid line in the graph above, at the vertical line (when mealcent is 0).
graph twoway line yhat1 yhat2 yhat3 mealcent, /// xlabel(-50 -40 to 50) ylabel(0 .1 to 1) ytitle(Predicted Probability) /// sort scheme(s2mono) xline(0)
Both of these individual effects are not significant. We can test the overall effect of _Icred_2 and _Icred_3 using the test command as shown below. Note we need to first re-run the original logistic regression with all 3 groups since we had run the separate logistic regressions previously, and we use quietly before the command to suppress the output.
quietly xi: logit hiqual i.cred*mealcent quietly xi: logistic hiqual i.cred*mealcent test _Icred_2 _Icred_3
( 1) _Icred_2 = 0.0
( 2) _Icred_3 = 0.0
chi2( 2) = 0.99
Prob > chi2 = 0.6098
Note that we could also use the lrtest command as illustrated in lesson 1 to perform this test using a likelihood ratio test. Note that these give much the same result. Note that i.cred|mealcent is the same as i.cred*mealcent but omits the main effects for i.cred.
estimates store model1
xi: logit hiqual i.cred|mealcent
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred|mealcent _IcreXmealc_# (coded as above)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -376.6609
Iteration 2: log likelihood = -319.1809
Iteration 3: log likelihood = -306.47587
Iteration 4: log likelihood = -305.07359
Iteration 5: log likelihood = -305.04574
Iteration 6: log likelihood = -305.04573
Logistic regression Number of obs = 1200
LR chi2(3) = 904.76
Prob > chi2 = 0.0000
Log likelihood = -305.04573 Pseudo R2 = 0.5973
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | -.0768575 .0095242 -8.07 0.000 -.0955246 -.0581904
_IcreXmeal~2 | -.031567 .012051 -2.62 0.009 -.0551866 -.0079474
_IcreXmeal~3 | -.0441854 .0111627 -3.96 0.000 -.0660638 -.022307
_cons | -2.162198 .156703 -13.80 0.000 -2.469331 -1.855066
------------------------------------------------------------------------------
xi: logistic hiqual i.cred|mealcent
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred|mealcent _IcreXmealc_# (coded as above)
Logit estimates Number of obs = 1200
LR chi2(3) = 904.76
Prob > chi2 = 0.0000
Log likelihood = -305.04573 Pseudo R2 = 0.5973
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mealcent | .9260218 .0088196 -8.07 0.000 .908896 .9434703
_IcreXmeal~2 | .968926 .0116766 -2.62 0.009 .9463085 .9920841
_IcreXmeal~3 | .9567766 .0106802 -3.96 0.000 .9360711 .97794
------------------------------------------------------------------------------
lrtest . model1
Logistic: likelihood-ratio test chi2(2) = 1.04
Prob > chi2 = 0.5938
Say that we had wanted to test the effect of cred when meals was 40. We could do this by centering meals around 40 as shown below and then re-running the logistic regression.
generate meal40 = meals - 40
xi: logit hiqual i.cred*meal40
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred*meal40 _IcreXmeal4_# (coded as above)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -375.90054
Iteration 2: log likelihood = -319.1446
Iteration 3: log likelihood = -306.19596
Iteration 4: log likelihood = -304.60217
Iteration 5: log likelihood = -304.52497
Iteration 6: log likelihood = -304.52455
Logistic regression Number of obs = 1200
LR chi2(5) = 905.80
Prob > chi2 = 0.0000
Log likelihood = -304.52455 Pseudo R2 = 0.5979
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | .6450093 .3127673 2.06 0.039 .0319966 1.258022
_Icred_3 | .7702654 .3004048 2.56 0.010 .1814829 1.359048
meal40 | -.0817427 .0114861 -7.12 0.000 -.1042552 -.0592303
_IcreXmeal~2 | -.0222125 .0164332 -1.35 0.176 -.054421 .0099959
_IcreXmeal~3 | -.0364404 .0153391 -2.38 0.018 -.0665044 -.0063763
_cons | -1.408828 .2483308 -5.67 0.000 -1.895547 -.9221083
------------------------------------------------------------------------------
xi: logistic hiqual i.cred*meal40
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred*meal40 _IcreXmeal4_# (coded as above)
Logit estimates Number of obs = 1200
LR chi2(5) = 905.80
Prob > chi2 = 0.0000
Log likelihood = -304.52455 Pseudo R2 = 0.5979
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Icred_2 | 1.906005 .596136 2.06 0.039 1.032514 3.518455
_Icred_3 | 2.160339 .6489762 2.56 0.010 1.198994 3.892485
meal40 | .921509 .0105846 -7.12 0.000 .9009954 .9424897
_IcreXmeal~2 | .9780324 .0160722 -1.35 0.176 .9470334 1.010046
_IcreXmeal~3 | .9642156 .0147902 -2.38 0.018 .9356588 .993644
------------------------------------------------------------------------------
test _Icred_2 _Icred_3
( 1) _Icred_2 = 0.0
( 2) _Icred_3 = 0.0
chi2( 2) = 6.83
Prob > chi2 = 0.0329
Instead of the test command, we could have used lrtest to perform a likelihood ratio test as we showed previously.
estimates store model2
xi: logit hiqual i.cred|meal40
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred|meal40 _IcreXmeal4_# (coded as above)
Iteration 0: log likelihood = -757.42622
Iteration 1: log likelihood = -381.456
Iteration 2: log likelihood = -322.22663
Iteration 3: log likelihood = -309.37594
Iteration 4: log likelihood = -308.13895
Iteration 5: log likelihood = -308.11346
Iteration 6: log likelihood = -308.11344
Logistic regression Number of obs = 1200
LR chi2(3) = 898.63
Prob > chi2 = 0.0000
Log likelihood = -308.11344 Pseudo R2 = 0.5932
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meal40 | -.0816905 .0102262 -7.99 0.000 -.1017335 -.0616475
_IcreXmeal~2 | -.0246449 .01547 -1.59 0.111 -.0549655 .0056757
_IcreXmeal~3 | -.0432141 .014391 -3.00 0.003 -.0714199 -.0150082
_cons | -.8618526 .115093 -7.49 0.000 -1.087431 -.6362744
------------------------------------------------------------------------------
xi: logistic hiqual i.cred|meal40
i.cred _Icred_1-3 (naturally coded; _Icred_1 omitted)
i.cred|meal40 _IcreXmeal4_# (coded as above)
Logit estimates Number of obs = 1200
LR chi2(3) = 898.63
Prob > chi2 = 0.0000
Log likelihood = -308.11344 Pseudo R2 = 0.5932
------------------------------------------------------------------------------
hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
meal40 | .9215572 .009424 -7.99 0.000 .9032703 .9402143
_IcreXmeal~2 | .9756563 .0150934 -1.59 0.111 .9465178 1.005692
_IcreXmeal~3 | .9577064 .0137824 -3.00 0.003 .9310708 .9851038
------------------------------------------------------------------------------
lrtest . model2
Logistic: likelihood-ratio test chi2(2) = 7.18
Prob > chi2 = 0.0276
These results show that the overall effect of cred is significant when meals is 40. In particular, odds ratio for _Icred_3 is 2.160339, indicating that high credentialed schools have an odds about 2.16 times that of low credentialed schools of being high quality when the percent of students receiving free meals is 40%. This effect is statistically significant. Likewise the odds ratio for _Icred_2 is about 1.9, indicating that medium credentialed schools have an odds about 1.9 times that of low credentialed schools of being high quality when meals is 40%, and this is also significant.
2.4 More on Interpreting Coefficients and Odds Ratios
At the start of this chapter, we noted that if you understand how to interpret coefficients for models with categorical variables with OLS regression, then this will help you be able to interpret coefficients and odds ratios in logistic regression. In fact, the interpretation of coefficients for OLS and logistic regression are identical, except that in OLS the outcome variable is the dependent variable, whereas in logistic regression the outcome variable is the "log odds of the outcome variable being 1". Aside from this difference, the interpretation of the coefficients is the same because both of these methods are linear models. However, it is much easier to interpret odds ratios than it is to interpret coefficients but the meaning of the odds ratios does not have a direct relationship to OLS like the coefficients. Where OLS (and logistic regression coefficients) form comparisons by subtraction, we have seen that odds ratios form comparisons by division. We illustrate this below with a small fictitious data file that has one outcome variable y, two categorical predictors x1 and x2 and a variable representing the product of these two variables, x12. You can access this file from within Stata like this.
use https://stats.idre.ucla.edu/stat/stata/webbooks/logistic/compare
We then analyze this data using OLS (via the regress command), using logistic regression with coefficients (with the logit command) and using logistic regression with odds ratios (via the logistic command). The table below shows the commands issued to obtain these 3 analyses, and the results of the respective 3 regressions and the predicted values broken down by x1 and x2. We then show the interpretation of the coefficient (in the case of OLS and Logistic using Logits) and the odds ratio (in the case of using Logistic with Odds Ratios). Let’s compare the coefficients/odds ratios for these analyses with respect to the predicted values in each analysis.
Note the similarity in the coefficients for OLS and logistic with respect to their predicted values. The coefficient for x1 in OLS compares, when x2 is 0, the predicted value when x1 is 1 minus the predicted value when x1 is 0, .666 – .5. Likewise, the coefficient for x1 in Logistic with Logits compares, when x2 is 0, the predicted value when x1 is 1 minus the predicted value when x1 is 0, .693 – .0. Even though the predicted values are different, the relationship between the predicted values and the coefficients is the same. Now, compare these two methods with Logistic with Odds Ratios. For that analysis, the coefficient for x1 compares, when x2 is 0, the predicted value when x1 is 1 divided by the predicted value x1 is 0, 2 / 1. Note that all three of these methods are comparing, when x2 is 0, the predicted value when x1 is 1 to the predicted value when x1 is 0, but OLS and Logistic with Logits makes this comparison by subtraction whereas Logistic with Odds Ratios makes this comparison by division. If you examine the predicted values and the interpretation of the odds ratios/coefficients for these three methods for x2 and for x12 you will see that this same relationship holds.
Likewise, this holds true for the other examples shown in this chapter. If you knew how to interpret the coefficients using OLS regression, you could then infer the interpretation of the coefficients when using Logistic with Logits and when using Logistic with Odds Ratios. The main leap is that when OLS makes comparisons using subtraction, you would substitute the subtraction with division to arrive at the comparisons that would be made using Logistic with Odds Ratios.
| OLS | Logistic with Logits | Logistic with Odds Ratios | |
| Stata Command for analysis |
. regress y x1 x2 x12 adjust , by(x1 x2) |
. logit y x1 x2 x12 adjust , by(x1 x2) |
. logistic y x1 x2 x12 adjust , by(x1 x2) exp |
| Regression Results |
x1 .166 x2 .3 x12 .018 _cons .5 |
x1 .693 x2 1.386 x12 2.079 _cons 0.0 |
x1 2 x2 4 x12 8 |
| Predicted Values by x1 and x2. |
| x2 x1 | 0 1 ---+---------- 0 | .5 .8 1 | .666 .984 |
| x2 x1 | 0 1 ----+----------- 0 | 0 1.386 1 | .693 4.158 |
| x2 x1 | 0 1 ----+----------- 0 | 1 4 1 | 2 64 |
| Interpretation of coefficient/odds ratio for X1 | The difference between .666 and .5 = .166, (the effect of x1 when x2 is 0). | The difference between .693 and 0 = .693, (the effect of x1 when x2 is 0). | The ratio of 2 / 1, (the effect of x1 when x2 is 0). |
| Interpretation of coefficient/odds ratio for X2 | The difference between .8 and .5 = .3, (the effect of x2 when x1 is 0). | The difference between 1.386 and 0 = 1.386, (the effect of x2 when x1 is 0). | The ratio of 4 / 1, (the effect of x2 when x1 is 0). |
| Interpretation of coefficient/odds ratio for X12 | The difference between (.984 – .8) and (.666 – 5) = .018, (the effect of x1 when x2=1 minus the effect of x1 when x2=0). | The difference between (4.15 – 1.38) and (.693 – 0) = 2.077, (the effect of x1 when x2=1 minus the effect of x1 when x2=0). | The ratio of (64 / 4) divided by ( 2 / 1), (the effect of x1 when x2=1 divided by the effect of x1 when x2=0). |
| Notes on interpretation | Note that the interpretation of the results is identical to OLS. The only difference is the predicted value is a "Logit", but the relationship between the coefficients and the predicted values is the same as with OLS. | The interpretation of the results similar to OLS and Logits, except that the coefficients in OLS and Logits reflect the differences in predicted values, the Odds Ratios reflect the ratios of the predicted values. |
2.5 Summary
This chapter has covered a variety of logistic models involving categorical predictors, including models with a single categorical predictor, with two categorical predictors with just main effects, models with two categorical predictors with an interaction, models with continuous and categorical predictors with just main effects and models with continuous and categorical predictors with an interaction. The interpretation of the results from a simple logistic regression can be very tricky, and as we have seen in this chapter it is important to exercise extra caution in interpreting the results of models with categorical predictors, especially if your models have interactions. In the presence of interactions, the meaning of the lower order effects changes and they need to be interpreted in light of the interaction.
If the interaction involves two categorical variables (say x1 and x2), we showed examples illustrating that tables showing the predicted values broken down by x1 and x2 can be useful in seeing the nature of the interaction, and for relating the tests formed by the coefficients to the predicted odds ratios (or predicted probabilities). If the interaction is between a continuous variable (say x1) and a categorical variable (say x2) then showing graphs of the predicted probabilities by x1 with separate lines for x2 is a useful way of illustrating the interaction. This allows you to see how the lines are not parallel and allows you to visualize making comparisons of the categorical variable at certain levels of the continuous variable.
The examples from this chapter showed how important it is to test for and, when needed, include such interaction terms because if such an interaction is present in the data, but not in your model, the predicted values can be quite discrepant from the actual data, leading to poor model fit and a poorer understanding of your data. The next chapter will address diagnostics when using logistic regression to help you assess the quality of your model and to see whether it is accurately reflecting your data.