We will begin our discussion of binomial logistic regression by comparing it to regular ordinary least squares (OLS) regression. Perhaps the most obvious difference between the two is that in OLS regression the dependent variable is continuous and in binomial logistic regression, it is binary and coded as 0 and 1. Because the dependent variable is binary, different assumptions are made in logistic regression than are made in OLS regression, and we will discuss these assumptions later. Logistic regression is similar to OLS regression in that it is used to determine which predictor variables are statistically significant, diagnostics are used to check that the assumptions are valid, a test-statistic is calculated that indicates if the overall model is statistically significant, and a coefficient and standard error for each of the predictor variables is calculated.
To illustrate the difference between OLS and logistic regression, let’s see what happens when data with a binary outcome variable is analyzed using OLS regression. For the examples in this chapter, we will use a set of data collected by the state of California from 1200 high schools measuring academic achievement. Our dependent variable is called hiqual. This variable was created from a continuous variable (api00) using a cut-off point of 745. Hence, values of 744 and below were coded as 0 (with a label of "not_high_qual") and values of 745 and above were coded as 1 (with a label of "high_qual"). Our predictor variable will be a continuous variable called avg_ed, which is a continuous measure of the average education (ranging from 1 to 5) of the parents of the students in the participating high schools. After running the regression, we will obtain the fitted values and then graph them against observed variables.
NOTE: You will notice that although there are 1200 observations in the data set, only 1158 of them are used in the analysis below. Cases with missing values on any variable used in the analysis have been dropped (listwise deletion). We will discuss this issue further later on in the chapter.
use https://stats.idre.ucla.edu/stat/stata/webbooks/logistic/apilog, clear regress hiqual avg_ed
Source | SS df MS Number of obs = 1158
-------------+------------------------------ F( 1, 1156) = 1136.02
Model | 126.023363 1 126.023363 Prob > F = 0.0000
Residual | 128.240023 1156 .110934276 R-squared = 0.4956
-------------+------------------------------ Adj R-squared = 0.4952
Total | 254.263385 1157 .219760921 Root MSE = .33307
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
avg_ed | .4286426 .0127175 33.70 0.000 .4036906 .4535946
_cons | -.8549049 .0363655 -23.51 0.000 -.9262547 -.7835551
------------------------------------------------------------------------------
predict yhat
(option xb assumed; fitted values) (42 missing values generated)
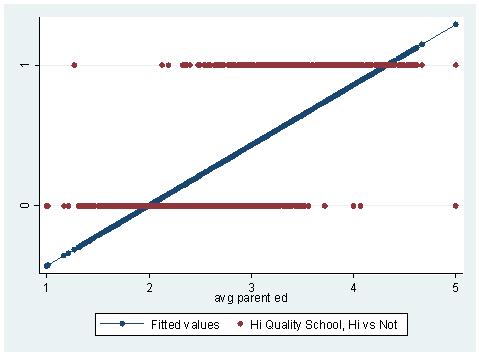
twoway scatter yhat hiqual avg_ed, connect(l .) symbol(i O) sort ylabel(0 1)
In the graph above, we have plotted the predicted values (called "fitted values" in the legend, the blue line) along with the observed data values (the red dots). Upon inspecting the graph, you will notice that some things that do not make sense. First, there are predicted values that are less than zero and others that are greater than +1. Such values are not possible with our outcome variable. Also, the line does a poor job of "fitting" or "describing" the data points. Now let’s try running the same analysis with a logistic regression.
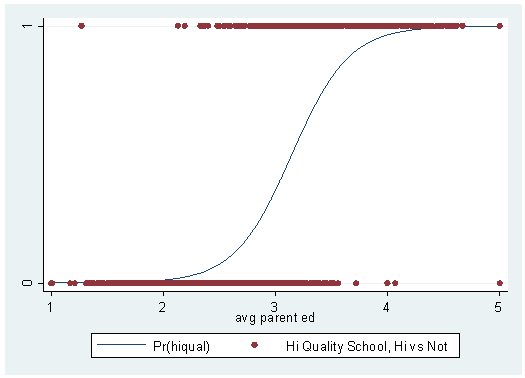
logit hiqual avg_ed Iteration 0: log likelihood = -730.68708 Iteration 1: log likelihood = -414.55532 Iteration 2: log likelihood = -364.17926 Iteration 3: log likelihood = -354.51979 Iteration 4: log likelihood = -353.92042 Iteration 5: log likelihood = -353.91719 Logistic regression Number of obs = 1158 LR chi2(1) = 753.54 Prob > chi2 = 0.0000 Log likelihood = -353.91719 Pseudo R2 = 0.5156 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- avg_ed | 3.909635 .2383083 16.41 0.000 3.442559 4.376711 _cons | -12.30054 .7314646 -16.82 0.000 -13.73418 -10.86689 ------------------------------------------------------------------------------ predict yhat1 (option p assumed; Pr(hiqual)) (42 missing values generated)twoway scatter yhat1 hiqual avg_ed, connect(l i) msymbol(i O) sort ylabel(0 1)
As before, we have calculated the predicted probabilities and have graphed them against the observed values. With the logistic regression, we get predicted probabilities that make sense: no predicted probabilities is less than zero or greater than one. Also, the logistic regression curve does a much better job of "fitting" or "describing" the data points.
Terminology
Now that we have seen an example of a logistic regression analysis, let’s spend a little time discussing the vocabulary involved. So let’s begin by defining the various terms that are frequently encountered, discuss how these terms are related to one another and how they are used to explain the results of the logistic regression. Probability is defined as the quantitative expression of the chance that an event will occur. More formally, it is the number of times the event "occurs" divided by the number of times the event "could occur". For a simple example, let’s consider tossing a coin. On average, you get heads once out of every two tosses. Hence, the probability of getting heads is 1/2 or .5.
Next let’s consider the odds. In common parlance, probability and odds are used interchangeably. However, in statistics, probability and odds are not the same. The odds of an event happening is defined as the probability that the event occurs divided by the probability that the event does not occur. To continue with our coin-tossing example, the probability of getting heads is .5 and the probability of not getting heads (i.e., getting tails) is also .5. Hence, the odds are .5/.5 = 1. Note that the probability of an event happening and its compliment, the probability of the event not happening, must sum to 1. Now let’s pretend that we alter the coin so that the probability of getting heads is .6. The probability of not getting heads is then .4. The odds of getting heads is .6/.4 = 1.5. If we had altered the coin so that the probability of getting heads was .8, then the odds of getting heads would have been .8/.2 = 4. As you can see, when the odds equal one, the probability of the event happening is equal to the probability of the event not happening. When the odds are greater than one, the probability of the event happening is higher than the probability of the event not happening, and when the odds are less than one, the probability of the event happening is less than the probability of the event not happening. Also note that odds can be converted back into a probability: probability = odds / (1+odds).
Now let’s consider an odds ratio. As the name suggests, it is the ratio of two odds. Let’s say we have males and females who want to join a team. Let’s say that 75% of the women and 60% of men make the team. So the odds for women are .75/.25 = 3, and for men the odds are .6/.4 = 1.5. The odds ratio would be 3/1.5 = 2, meaning that the odds are 2 to 1 that a woman will make the team compared to men.
Another term that needs some explaining is log odds, also known as logit. Log odds are the natural logarithm of the odds. The coefficients in the output of the logistic regression are given in units of log odds. Therefore, the coefficients indicate the amount of change expected in the log odds when there is a one unit change in the predictor variable with all of the other variables in the model held constant. In a while we will explain why the coefficients are given in log odds. Please be aware that any time a logarithm is discussed in this chapter, we mean the natural log.
In summary:
- probability: the number of times the event occurs divided by the number of times the event could occur (possible values range from 0 to 1)
- odds: the probability that an event will occur divided by the probability that the event will not occur: probability(success) / probability(failure)
- odds ratio: the ratio of the odds of success for one group divided by the odds of success for the other group: ( probability(success)A/probability(failure)A ) / ( probability(success)B/probability(failure)B )
- log odds: the natural log of the odds
The orcalc command (as in odds ratio calculation) can be used to obtain odds ratios. You will have to download the command by typing search orcalc. (see How can I use the search command to search for programs and get additional help? for more information about using search). To use this command, simply provide the two probabilities to be used (the probability of success for group 1 is given first, then the probability of success for group 2). For example,
orcalc .3 .4
Odds ratio for group 2 vs group 1 p2 / (1 - p2) odds2 0.40 / (1 - 0.40) 0.667 or = --------------- = ------- = ------------------- = ------- = 1.556 p1 / (1 - p1) odds1 0.30 / (1 - 0.30) 0.429
At this point we need to pause for a brief discussion regarding the coding of data. Logistic regression not only assumes that the dependent variable is dichotomous, it also assumes that it is binary; in other words, coded as 0 and +1. These codes must be numeric (i.e., not string), and it is customary for 0 to indicate that the event did not occur and for 1 to indicate that the event did occur. Many statistical packages, including Stata, will not perform logistic regression unless the dependent variable coded 0 and 1. Specifically, Stata assumes that all non-zero values of the dependent variables are 1. Therefore, if the dependent variable was coded 3 and 4, which would make it a dichotomous variable, Stata would regard all of the values as 1. This is hard-coded into Stata; there are no options to over-ride this. If your dependent variable is coded in any way other than 0 and 1, you will need to recode it before running the logistic regression. (NOTE: SAS assumes that 0 indicates that the event happened; use the descending option on the proc logistic statement to have SAS model the 1’s.) By default, Stata predicts the probability of the event happening.
Stata’s logit and logistic commands
Stata has two commands for logistic regression, logit and logistic. The main difference between the two is that the former displays the coefficients and the latter displays the odds ratios. You can also obtain the odds ratios by using the logit command with the or option. Which command you use is a matter of personal preference. Below, we discuss the relationship between the coefficients and the odds ratios and show how one can be converted into the other. However, before we discuss some examples of logistic regression, we need to take a moment to review some basic math regarding logarithms. In this web book, all logarithms will be natural logs. If log(a)=b then exp(b) = a. For example, log(5) = 1.6094379 and exp(1.6094379) = 5, where "exp" indicates exponentiation. This is critical, as it is the relationship between the coefficients and the odds ratios.
We have created some small data sets to help illustrate the relationship between the logit coefficients (given in the output of the logit command) and the odds ratios (given in the output of the logistic command). We will use the tabulate command to see how the data are distributed. We will also obtain the predicted values and graph them against x, as we would in OLS regression.
clear input y x cnt
y x cnt 1. 0 0 10 2. 0 1 10 3. 1 0 10 4. 1 1 10 5. endexpand cnt (36 observations created)
We use the expand command here for ease of data entry. On each line we enter the x and y values, and for the variable cnt, we enter then number of times we want that line repeated in the data set. We use the expand command to finish creating the data set. We can see this by using the list command. If list command is issued by itself (i.e., with no variables after it), Stata will list all observations for all variables.
list
y x cnt 1. 0 0 10 2. 0 1 10 3. 1 0 10 4. 1 1 10 5. 0 0 10 6. 0 0 10 7. 0 0 10 8. 0 0 10 9. 0 0 10 10. 0 0 10 11. 0 0 10 12. 0 0 10 13. 0 0 10 14. 0 1 10 15. 0 1 10 16. 0 1 10 17. 0 1 10 18. 0 1 10 19. 0 1 10 20. 0 1 10 21. 0 1 10 22. 0 1 10 23. 1 0 10 24. 1 0 10 25. 1 0 10 26. 1 0 10 27. 1 0 10 28. 1 0 10 29. 1 0 10 30. 1 0 10 31. 1 0 10 32. 1 1 10 33. 1 1 10 34. 1 1 10 35. 1 1 10 36. 1 1 10 37. 1 1 10 38. 1 1 10 39. 1 1 10 40. 1 1 10tabulate y x, col
| x y | 0 1 | Total -----------+----------------------+---------- 0 | 10 10 | 20 | 50.00 50.00 | 50.00 -----------+----------------------+---------- 1 | 10 10 | 20 | 50.00 50.00 | 50.00 -----------+----------------------+---------- Total | 20 20 | 40 | 100.00 100.00 | 100.00logit y x
Iteration 0: log likelihood = -27.725887 Logit estimates Number of obs = 40 LR chi2(1) = 0.00 Prob > chi2 = 1.0000 Log likelihood = -27.725887 Pseudo R2 = 0.0000 ------------------------------------------------------------------------------ y | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 0 .6324555 0.00 1.000 -1.23959 1.23959 _cons | 0 .4472136 0.00 1.000 -.8765225 .8765225 ------------------------------------------------------------------------------logit y x, or
Iteration 0: log likelihood = -27.725887 Logit estimates Number of obs = 40 LR chi2(1) = 0.00 Prob > chi2 = 1.0000 Log likelihood = -27.725887 Pseudo R2 = 0.0000 ------------------------------------------------------------------------------ y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 1 .6324555 0.00 1.000 .2895029 3.454197 ------------------------------------------------------------------------------logistic y x
Logit estimates Number of obs = 40 LR chi2(1) = 0.00 Prob > chi2 = 1.0000 Log likelihood = -27.725887 Pseudo R2 = 0.0000 ------------------------------------------------------------------------------ y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 1 .6324555 0.00 1.000 .2895029 3.454197 ------------------------------------------------------------------------------
In this example, we compared the output from the logit and the logistic commands. Later in this chapter, we will use probabilities to assist with the interpretation of the findings. Many people find probabilities easier to understand than odds ratios. You will notice that the information at the top of the two outputs is the same. Wald test values (called z) and the p-values are the same, as are the log likelihood and the standard error. However, the logit command gives coefficients and their confidence intervals, while the logistic command give odds ratios and their confidence intervals. You will also notice that the logistic command does not give any information regarding the constant, because it does not make much sense to talk about a constant with odds ratios. (The constant (_cons) is displayed with the coefficients because you would use both of the values to write out the equation for the logistic regression model.) Let’s start with the output regarding the variable x. The output from the logit command indicates that the coefficient of x is 0. This means that with a one unit change in x, you would predict a 0 unit change in y. To transform the coefficient into an odds ratio, take the exponential of the coefficient:
display exp(0)
1
This yields 1, which is the odds ratio. An odds ratio of 1 means that there is no effect of x on y. Looking at the z test statistic, we see that it is not statistically significant, and the confidence interval of the coefficient includes 0. Note that when there is no effect, the confidence interval of the odds ratio will include 1.
Next, let us try an example where the cell counts are not equal.
clear input y x cnt
y x cnt 1. 0 0 20 2. 0 1 20 3. 1 0 10 4. 1 1 10 5. endexpand cnt
(56 observations created)tabulate y x, col
| x y | 0 1 | Total -----------+----------------------+---------- 0 | 20 20 | 40 | 66.67 66.67 | 66.67 -----------+----------------------+---------- 1 | 10 10 | 20 | 33.33 33.33 | 33.33 -----------+----------------------+---------- Total | 30 30 | 60 | 100.00 100.00 | 100.00logit y x
Iteration 0: log likelihood = -38.19085 Logit estimates Number of obs = 60 LR chi2(1) = 0.00 Prob > chi2 = 1.0000 Log likelihood = -38.19085 Pseudo R2 = 0.0000 ------------------------------------------------------------------------------ y | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 1.70e-15 .5477226 0.00 1.000 -1.073516 1.073516 _cons | -.6931472 .3872983 -1.79 0.074 -1.452238 .0659436 ------------------------------------------------------------------------------logistic y x
Logit estimates Number of obs = 60 LR chi2(1) = 0.00 Prob > chi2 = 1.0000 Log likelihood = -38.19085 Pseudo R2 = 0.0000 ------------------------------------------------------------------------------ y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 1 .5477226 0.00 1.000 .3418045 2.925649 ------------------------------------------------------------------------------
In this example, we see that the coefficient of x is again 0 (1.70e-15 is approximately 0, with rounding error) and hence, the odds ratio is 1. Again, we conclude that x has no statistically significant effect on y. However, in this example, the constant is not 0. The constant is the odds of y = 1 when x = 0. The constant (also called the intercept) is the predicted log odds when all of the variables in the model are held equal to 0.
Now, let’s look at an example where the odds ratio is not 1.
clear input y x cnt
y x cnt 1. 0 0 10 2. 0 1 10 3. 1 0 10 4. 1 1 40 5. endexpand cnt
(66 observations created)tabulate y x, col
| x y | 0 1 | Total -----------+----------------------+---------- 0 | 10 10 | 20 | 50.00 20.00 | 28.57 -----------+----------------------+---------- 1 | 10 40 | 50 | 50.00 80.00 | 71.43 -----------+----------------------+---------- Total | 20 50 | 70 | 100.00 100.00 | 100.00logit y x
Iteration 0: log likelihood = -41.878871 Iteration 1: log likelihood = -38.937828 Iteration 2: log likelihood = -38.883067 Iteration 3: log likelihood = -38.883065 Logit estimates Number of obs = 70 LR chi2(1) = 5.99 Prob > chi2 = 0.0144 Log likelihood = -38.883065 Pseudo R2 = 0.0715 ------------------------------------------------------------------------------ y | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 1.386294 .5700877 2.43 0.015 .268943 2.503646 _cons | -1.12e-15 .4472136 -0.00 1.000 -.8765225 .8765225 ------------------------------------------------------------------------------logistic y x
Logit estimates Number of obs = 70 LR chi2(1) = 5.99 Prob > chi2 = 0.0144 Log likelihood = -38.883065 Pseudo R2 = 0.0715 ------------------------------------------------------------------------------ y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- x | 4 2.280351 2.43 0.015 1.308581 12.22699 ------------------------------------------------------------------------------
Here we see that the odds ratio is 4, or more precisely, 4 to 1. In other words, the odds for the group coded as 1 are four times that as the odds for the group coded as 0.
A single dichotomous predictor
Let’s use again the data from our first example. Our predictor variable will be a dichotomous variable, yr_rnd, indicating if the school is on a year-round calendar (coded as 1) or not (coded as 0). First, let’s tabulate and then graph the variables to get an idea of what the data look like.
use https://stats.idre.ucla.edu/stat/stata/webbooks/logistic/apilog, clear tab2 hiqual yr_rnd
-> tabulation of hiqual by yr_rnd Hi Quality | School, Hi | Year Round School vs Not | not_yrrnd yrrnd | Total -----------+----------------------+---------- not high | 613 196 | 809 high | 371 20 | 391 -----------+----------------------+---------- Total | 984 216 | 1200scatter hiqual yr_rnd, jitter(6)
Because both of our variables are dichotomous, we have used the jitter option so that the points are not exactly one on top of the other. Now let’s look at the logistic regression.
logit hiqual yr_rnd
Iteration 0: log likelihood = -757.42622 Iteration 1: log likelihood = -721.1619 Iteration 2: log likelihood = -718.68705 Iteration 3: log likelihood = -718.62629 Iteration 4: log likelihood = -718.62623 Logit estimates Number of obs = 1200 LR chi2(1) = 77.60 Prob > chi2 = 0.0000 Log likelihood = -718.62623 Pseudo R2 = 0.0512 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | -1.78022 .2437799 -7.30 0.000 -2.258019 -1.30242 _cons | -.5021629 .065778 -7.63 0.000 -.6310853 -.3732405 ------------------------------------------------------------------------------
While we will briefly discuss the outputs from the logit and logistic commands, please see our Annotated Output pages for a more complete treatment. Let’s start at the top of the output. The meaning of the iteration log will be discussed later. Next, you will notice that the overall model is statistically significant (chi-square = 77.60, p = .00). This means that the model that includes yr_rnd fits the data statistically significantly better than the model without it (i.e., a model with only the constant). We will not try to interpret the meaning of the "pseudo R-squared" here except to say that emphasis should be put on the term "pseudo" and to note that some authors (including Hosmer and Lemeshow, 2000) discount the usefulness of this statistic. The log likelihood of the fitted model is -718.62623. The likelihood is the probability of observing a given set of observations, given the value of the parameters. The number -718.62623 in and of itself does not have much meaning; rather, it is used in a calculation to determine if a reduced model fits significantly better than the full model and for comparisons to other models.
The coefficient for yr_rnd is -1.78. This indicates that a decrease of 1.78 is expected in the log odds of hiqual with a one-unit increase in yr_rnd (in other words, for students in a year-round school compared to those who are not). This coefficient is also statistically significant, with a Wald test value (z) of -7.30. Because the Wald test is statistically significant, the confidence interval for the coefficient does not include 0. As before, the coefficient can be converted into an odds ratio by exponentiating it:
display exp(-1.78022)
.16860105
You can obtain the odds ratio from Stata either by issuing the logistic command or by using the or option with the logit command.
logistic hiqual yr_rnd
Logit estimates Number of obs = 1200 LR chi2(1) = 77.60 Prob > chi2 = 0.0000 Log likelihood = -718.62623 Pseudo R2 = 0.0512 ------------------------------------------------------------------------------ hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | .1686011 .0411016 -7.30 0.000 .1045574 .2718732 ------------------------------------------------------------------------------logit hiqual yr_rnd, or
Iteration 0: log likelihood = -757.42622 Iteration 1: log likelihood = -721.1619 Iteration 2: log likelihood = -718.68705 Iteration 3: log likelihood = -718.62629 Iteration 4: log likelihood = -718.62623 Logit estimates Number of obs = 1200 LR chi2(1) = 77.60 Prob > chi2 = 0.0000 Log likelihood = -718.62623 Pseudo R2 = 0.0512 ------------------------------------------------------------------------------ hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | .1686011 .0411016 -7.30 0.000 .1045574 .2718732 ------------------------------------------------------------------------------
You will notice that the only difference between these two outputs is that the logit command includes an iteration log at the top. Our point here is that you can use more than one method to get this information, and which one you use is up to you. The odds ratio is interpreted as a .1686011 change in the odds ratio when there is a one-unit change in yr_rnd. Notice that a .1686011 change is actually a decrease (because odds ratios less than 1 indicate a decrease; you can’t have a negative odds ratio). In other words, as you go from a non-year-round school to a year-round school, the ratio of the odds becomes smaller.
In the previous example, we used a dichotomous independent variable. Traditionally, when researchers and data analysts analyze the relationship between two dichotomous variables, they often think of a chi-square test. Let’s take a moment to look at the relationship between logistic regression and chi-square. Chi-square is actually a special case of logistic regression. In a chi-square analysis, both variables must be categorical, and neither variable is an independent or dependent variable (that distinction is not made). In logistic regression, while the dependent variable must be dichotomous, the independent variable can be dichotomous or continuous. Also, logistic regression is not limited to only one independent variable.
A single continuous predictor
Now let’s consider a model with a single continuous predictor. For this example we will be using a variable called avg_ed. This is a measure of the education achievements of the parents of the children in the schools that participated in the study. Let’s start off by summarizing and graphing this variable.
summarize avg_ed
Variable | Obs Mean Std. Dev. Min Max -------------+----------------------------------------------------- avg_ed | 1158 2.753964 .7699517 1 5scatter hiqual avg_edlogit hiqual avg_ed
Iteration 0: log likelihood = -730.68708 Iteration 1: log likelihood = -414.55532 Iteration 2: log likelihood = -364.17926 Iteration 3: log likelihood = -354.51979 Iteration 4: log likelihood = -353.92042 Iteration 5: log likelihood = -353.91719 Logit estimates Number of obs = 1158 LR chi2(1) = 753.54 Prob > chi2 = 0.0000 Log likelihood = -353.91719 Pseudo R2 = 0.5156 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- avg_ed | 3.909635 .2383083 16.41 0.000 3.442559 4.376711 _cons | -12.30054 .7314646 -16.82 0.000 -13.73418 -10.86689 ------------------------------------------------------------------------------logistic hiqual avg_ed
Logit estimates Number of obs = 1158 LR chi2(1) = 753.54 Prob > chi2 = 0.0000 Log likelihood = -353.91719 Pseudo R2 = 0.5156 ------------------------------------------------------------------------------ hiqual | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- avg_ed | 49.88075 11.887 16.41 0.000 31.26688 79.57586 ------------------------------------------------------------------------------
Looking at the output from the logit command, we see that the LR-chi-squared is very high and is clearly statistically significant. This means that the model that we specified, namely avg_ed predicting hiqual, is significantly better than the model with only the constant (i.e., just the dependent variable). The coefficient for avg_ed is 3.91, meaning that we expect an increase of 3.91 in the log odds of hiqual with every one-unit increase avg_ed. The value of the Wald statistic indicates that the coefficient is significantly different from 0. However, it is not obvious what a 3.91 increase in the log odds of hiqual really means. Therefore, let’s look at the output from the logistic command. This tells us that the odds ratio is 49.88. This is the amount of change expected in the odds ratio when there is a one unit change in the predictor variable with all of the other variables in the model held constant.
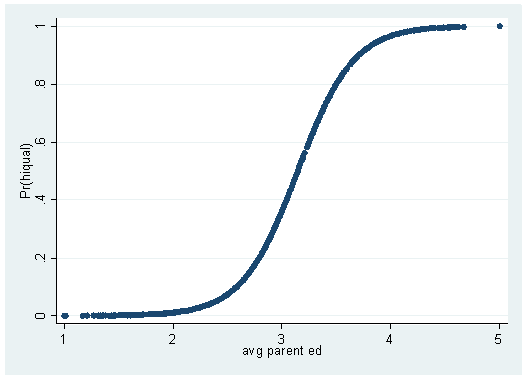
If we graph hiqual and avg_ed, you see that, like the graphs with the made-up data at the beginning of this chapter, it is not terribly informative. If you tried to draw a straight line through the points as you would in OLS regression, the line would not do a good job of describing the data. One possible solution to this problem is to transform the values of the dependent variable into predicted probabilities, as we did when we predicted yhat1 in the example at the beginning of this chapter. If we graph the predicted probabilities of hiqual against avg_ed, (a variable we will call yhatc) we see that a line curved somewhat like an S is formed. This s-shaped curve resembles some statistical distributions and can be used to generate a type of regression equation and its statistical tests. To get from the straight line seen in OLS to the s-shaped curve in logistic regression, we need to do some mathematical transformations. When looking at these formulas, it becomes clear why we need to talk about probabilities, natural logs and exponentials when talking about logistic regression.
predict yhatc
(option p assumed; Pr(hiqual)) (42 missing values generated)scatter yhatc avg_ed
Both a dichotomous and a continuous predictor
Now let’s try an example with both a dichotomous and a continuous independent variable.
logit hiqual yr_rnd avg_ed
Iteration 0: log likelihood = -730.68708 Iteration 1: log likelihood = -412.99872 Iteration 2: log likelihood = -360.19162 Iteration 3: log likelihood = -349.04893 Iteration 4: log likelihood = -348.22245 Iteration 5: log likelihood = -348.21614 Iteration 6: log likelihood = -348.21614 Logit estimates Number of obs = 1158 LR chi2(2) = 764.94 Prob > chi2 = 0.0000 Log likelihood = -348.21614 Pseudo R2 = 0.5234 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | -1.091301 .3425414 -3.19 0.001 -1.762669 -.4199316 avg_ed | 3.864344 .2410931 16.03 0.000 3.39181 4.336878 _cons | -12.05094 .7397089 -16.29 0.000 -13.50074 -10.60113 ------------------------------------------------------------------------------
Interpreting the output from this logistic regression is not much different from the previous ones. The LR-chi-square is very high and is statistically significant. This means that the model that we specified is significantly better at predicting hiqual than a model without the predictors yr_rnd and avg_ed. The coefficient for yr_rnd is -1.09 and means that we would expect a 1.09 unit decrease in the log odds of hiqual for every one-unit increase in yr_rnd, holding all other variables constant in the model. The coefficient for avg_ed is 3.86 and means that we would expect a 3.86 unit increase in the log odds of hiqual with every one-unit increase in avg_ed, with all other variables held constant. Both of these coefficients are significantly different from 0 according the Wald test.
Tools to assist with interpretation
In OLS regression, the R-square statistic indicates the proportion of the variability in the dependent variable that is accounted for by the model (i.e., all of the independent variables in the model). Unfortunately, creating a statistic to provide the same information for a logistic regression model has proved to be very difficult. Many people have tried, but no approach has been widely accepted by researchers or statisticians. The output from the logit and logistic commands give a statistic called "pseudo-R-square", and the emphasis is on the term "pseudo". This statistic should be used only to give the most general idea as to the proportion of variance that is being accounted for. The fitstat command gives a listing of various pseudo-R-squares. You can download fitstat over the internet (see How can I use the search command to search for programs and get additional help? for more information about using search).
fitstat
Measures of Fit for logistic of hiqual Log-Lik Intercept Only: -730.687 Log-Lik Full Model: -353.917 D(1156): 707.834 LR(1): 753.540 Prob > LR: 0.000 McFadden's R2: 0.516 McFadden's Adj R2: 0.513 Maximum Likelihood R2: 0.478 Cragg & Uhler's R2: 0.667 McKelvey and Zavoina's R2: 0.734 Efron's R2: 0.580 Variance of y*: 12.351 Variance of error: 3.290 Count R2: 0.871 Adj Count R2: 0.605 AIC: 0.615 AIC*n: 711.834 BIC: -7447.109 BIC": -746.485
As you can see from the output, some statistics indicate that the model fit is relatively good, while others indicate that it is not so good. The values are so different because they are measuring different things. We will not discuss the items in this output; rather, our point is to let you know that there is little agreement regarding an R-square statistic in logistic regression, and that different approaches lead to very different conclusions. If you use an R-square statistic at all, use it with great care.
Next, we will describe some tools that can used to help you better understand the logistic regressions that you have run. These commands are part of an .ado package called spost9_ado (see How can I use the search command to search for programs and get additional help? for more information about using search). (If you are using Stata 8, you want to get the spost .ado for that version.) The listcoef command gives you the logistic regression coefficients, the z-statistic from the Wald test and its p-value, the odds ratio, the standardized odds ratio and the standard deviation of x (i.e., the independent variables). We have included the help option so that the explanation of each column in the output is provided at the bottom. Two particularly useful columns are e^b, which gives the odds ratios and e^bStdX, which gives the change in the odds for a one standard deviation increase in x (i.e., yr_rnd and avg_ed).
listcoef, help
logit (N=1158): Factor Change in Odds
Odds of: high vs not_high
----------------------------------------------------------------------
hiqual | b z P>|z| e^b e^bStdX SDofX
-------------+--------------------------------------------------------
yr_rnd | -1.09130 -3.186 0.001 0.3358 0.6592 0.3819
avg_ed | 3.86434 16.028 0.000 47.6720 19.5966 0.7700
----------------------------------------------------------------------
b = raw coefficient
z = z-score for test of b=0
P>|z| = p-value for z-test
e^b = exp(b) = factor change in odds for unit increase in X
e^bStdX = exp(b*SD of X) = change in odds for SD increase in X
SDofX = standard deviation of X
The prtab command computes a table of predicted values for specified values of the independent variables listed in the model. Other independent variables are held constant at their mean by default.
prtab yr_rnd
logit: Predicted probabilities of positive outcome for hiqual ---------------------- Year | Round | School | Prediction ----------+----------- not_yrrnd | 0.1964 yrrnd | 0.0759 ---------------------- yr_rnd avg_ed x= .17702936 2.7539637
This command gives the predicted probability of being in a high quality school given the different levels of yr_rnd when avg_ed is held constant at its mean. Hence, when yr_rnd = 0 and avg_ed = 2.75, the predicted probability of being a high quality school is 0.1964. When yr_rnd = 1 and avg_ed = 2.75, the predicted probability of being a high quality school is 0.0759. Clearly, there is a much higher probability of being a high-quality school when the school is not on a year-round schedule than when it is. The "x = " at the bottom of the output gives the means of the x (i.e., independent) variables.
Let’s try the prtab command with a continuous variable to get a better understanding of what this command does and why it is useful. First, we need to run a logistic regression with a new variable and calculate the predicted values. Then, we will graph the predicted values against the variable. The variable that we will use is called meals, and it indicates the percent of students who receive free meals while at school.
logit hiqual meals
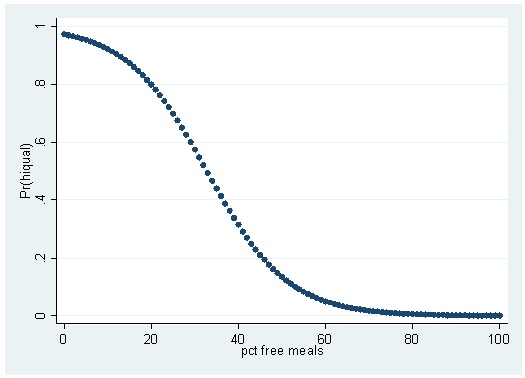
Iteration 0: log likelihood = -757.42622 Iteration 1: log likelihood = -393.8664 Iteration 2: log likelihood = -330.71607 Iteration 3: log likelihood = -314.26983 Iteration 4: log likelihood = -312.40166 Iteration 5: log likelihood = -312.36786 Iteration 6: log likelihood = -312.36785 Logit estimates Number of obs = 1200 LR chi2(1) = 890.12 Prob > chi2 = 0.0000 Log likelihood = -312.36785 Pseudo R2 = 0.5876 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- meals | -.107834 .0064069 -16.83 0.000 -.1203913 -.0952767 _cons | 3.531564 .235202 15.02 0.000 3.070577 3.992552 ------------------------------------------------------------------------------predict yhat, pr scatter yhat meals
Although this graph does not look like the classic s-shaped curve, it is another example of a logistic regression curve. It does not look like the curve formed using avg_ed because there is a positive relationship between avg_ed and hiqual, while there is a negative relationship between meals and hiqual. As you can tell, as the percent of free meals increases, the probability of being a high-quality school decreases. Now let’s compare this graph to the output of the prtab command. First you will need to set the matsize (matrix size) to 800. This will increase the maximum number of variables that Stata can use in model estimation.
set matsize 800 prtab meals
logit: Predicted probabilities of positive outcome for hiqual ---------------------- pct free | meals | Prediction ----------+----------- 0 | 0.9716 1 | 0.9684 2 | 0.9650 3 | 0.9611 4 | 0.9569 5 | 0.9522 6 | 0.9471 7 | 0.9414 8 | 0.9352 9 | 0.9283 10 | 0.9208 11 | 0.9126 12 | 0.9036 13 | 0.8938 14 | 0.8831 15 | 0.8715 16 | 0.8589 17 | 0.8453 18 | 0.8307 19 | 0.8150 20 | 0.7982 21 | 0.7802 22 | 0.7612 23 | 0.7410 24 | 0.7198 25 | 0.6976 26 | 0.6743 27 | 0.6502 28 | 0.6253 29 | 0.5997 30 | 0.5736 31 | 0.5470 32 | 0.5202 33 | 0.4933 34 | 0.4664 35 | 0.4396 36 | 0.4133 37 | 0.3874 38 | 0.3621 39 | 0.3376 40 | 0.3139 41 | 0.2912 42 | 0.2694 43 | 0.2487 44 | 0.2291 45 | 0.2107 46 | 0.1933 47 | 0.1770 48 | 0.1619 49 | 0.1478 50 | 0.1347 51 | 0.1226 52 | 0.1115 53 | 0.1012 54 | 0.0918 55 | 0.0832 56 | 0.0754 57 | 0.0682 58 | 0.0616 59 | 0.0557 60 | 0.0503 61 | 0.0454 62 | 0.0409 63 | 0.0369 64 | 0.0333 65 | 0.0300 66 | 0.0270 67 | 0.0243 68 | 0.0219 69 | 0.0197 70 | 0.0177 71 | 0.0159 72 | 0.0143 73 | 0.0129 74 | 0.0116 75 | 0.0104 76 | 0.0093 77 | 0.0084 78 | 0.0075 79 | 0.0068 80 | 0.0061 81 | 0.0055 82 | 0.0049 83 | 0.0044 84 | 0.0040 85 | 0.0036 86 | 0.0032 87 | 0.0029 88 | 0.0026 89 | 0.0023 90 | 0.0021 91 | 0.0019 92 | 0.0017 93 | 0.0015 94 | 0.0014 95 | 0.0012 96 | 0.0011 97 | 0.0010 98 | 0.0009 99 | 0.0008 100 | 0.0007 ---------------------- meals x= 52.15
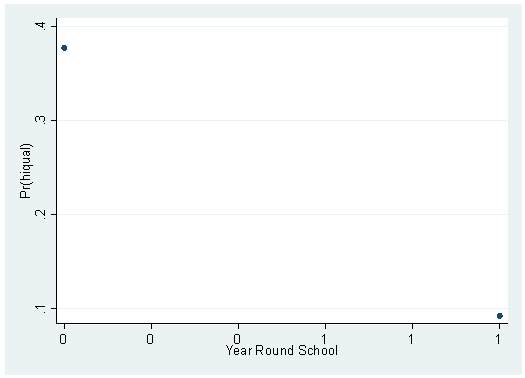
If you compare the output with the graph, you will see that they are two representations of the same things: the pair of numbers given on the first row of the prtab output are the coordinates for the left-most point on the graph and so on. If you try to make this graph using yr_rnd, you will see that the graph is not very informative: yr_rnd only has two possible values; hence, there are only two points on the graph.
drop yhat logit hiqual yr_rnd
Iteration 0: log likelihood = -757.42622 Iteration 1: log likelihood = -721.1619 Iteration 2: log likelihood = -718.68705 Iteration 3: log likelihood = -718.62629 Iteration 4: log likelihood = -718.62623 Logit estimates Number of obs = 1200 LR chi2(1) = 77.60 Prob > chi2 = 0.0000 Log likelihood = -718.62623 Pseudo R2 = 0.0512 ------------------------------------------------------------------------------ hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | -1.78022 .2437799 -7.30 0.000 -2.258019 -1.30242 _cons | -.5021629 .065778 -7.63 0.000 -.6310853 -.3732405 ------------------------------------------------------------------------------predict yhat, pr scatter yhat yr_rndprtab yr_rnd
logit: Predicted probabilities of positive outcome for hiqual ---------------------- Year | Round | School | Prediction ----------+----------- not_yrrnd | 0.3770 yrrnd | 0.0926 ---------------------- yr_rnd x= .18bsp; .18
Note that the values in this output are different than those seen previously because the models are different. In this example, we did not include avg_ed as a predictor, and here avg_ed is not being held constant at its mean.
The prchange command computes the change in the predicted probability as you go from a low value to a high value. We are going to use avg_ed for this example (its values range from 1 to5), because going from the low value to the high value on a 0/1 variable is not very interesting.
logit hiqual avg_ed
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -414.55532
Iteration 2: log likelihood = -364.17926
Iteration 3: log likelihood = -354.51979
Iteration 4: log likelihood = -353.92042
Iteration 5: log likelihood = -353.91719
Logistic regression Number of obs = 1158
LR chi2(1) = 753.54
Prob > chi2 = 0.0000
Log likelihood = -353.91719 Pseudo R2 = 0.5156
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
avg_ed | 3.909635 .2383083 16.41 0.000 3.442559 4.376711
_cons | -12.30054 .7314646 -16.82 0.000 -13.73418 -10.86689
------------------------------------------------------------------------------
prchange avg_ed
logit: Changes in Probabilities for hiqual
min->max 0->1 -+1/2 -+sd/2 MargEfct
avg_ed 0.9991 0.0002 0.5741 0.4472 0.5707
not_high high
Pr(y|x) 0.8225 0.1775
avg_ed
x= 2.75396
sd(x)= .769952
Let’s go through this output item by item to see what it is telling us. The min->max column indicates the amount of change that we should expect in the predicted probability of hiqual as avg_ed changes from its minimum value to its maximum value. The 0->1 column indicates the amount of change that we should expect in the predicted probability of hiqual as avg_ed changes from 0 to 1. For a variable like avg_ed, whose lowest value is 1, this column is not very useful, as it extrapolates outside of the observable range of avg_ed. The -+1/2 column indicates the amount of change that we should expect in the predicted probability of hiqual as avg_ed changes from the mean – 0.5 to the mean + 0.5. (i.e., half a unit either side of the mean). In other words, this is the rate of change of the slope at the mean of the function (look back at the logistic function graphed above). The -+sd/2 column gives the same information as the previous column, except that it is in standard deviations. The MargEfct column gives the largest possible change in the slope of the function. The Pr(y|x) part of the output gives the probability that hiqual equals zero given that the predictors are at their mean values and the probability that hiqual equals one given the predictors at their same mean values. Hence, the probability of being a not high quality school when avg_ed is at its mean value is .8225, and the probability of being a high quality school is .1775 when avg_ed is at the same mean value. The mean and the standard deviation of the x variable(s) are given at the bottom of the output.
Comparing models
Now that we have a model with two variables in it, we can ask if it is "better" than a model with just one of the variables in it. To do this, we use a command called lrtest, for likelihood ratio test. To use this command, you first run the model that you want to use as the basis for comparison (the full model). Next, you save the estimates with a name using the est store command. Next, you run the model that you want to compare to your full model, and then issue the lrtest command with the name of the full model. In our example, we will name our full model full_model. The output of this is a likelihood ratio test which tests the null hypothesis that the coefficients of the variable(s) left out of the reduced model is/are simultaneously equal to 0. In other words, the null hypothesis for this test is that removing the variable(s) has no effect; it does not lead to a poorer-fitting model. To demonstrate how this command works, let’s compare a model with both avg_ed and yr_rnd (the full model) to a model with only avg_ed in it (a reduced model).
logit hiqual yr_rnd avg_ed
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -412.99872
Iteration 2: log likelihood = -360.19162
Iteration 3: log likelihood = -349.04893
Iteration 4: log likelihood = -348.22245
Iteration 5: log likelihood = -348.21614
Iteration 6: log likelihood = -348.21614
Logistic regression Number of obs = 1158
LR chi2(2) = 764.94
Prob > chi2 = 0.0000
Log likelihood = -348.21614 Pseudo R2 = 0.5234
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -1.091301 .3425414 -3.19 0.001 -1.762669 -.4199316
avg_ed | 3.864344 .2410931 16.03 0.000 3.39181 4.336878
_cons | -12.05094 .7397089 -16.29 0.000 -13.50074 -10.60113
------------------------------------------------------------------------------
est store full_model
logit hiqual avg_ed if e(sample)
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -414.55532
Iteration 2: log likelihood = -364.17926
Iteration 3: log likelihood = -354.51979
Iteration 4: log likelihood = -353.92042
Iteration 5: log likelihood = -353.91719
Logistic regression Number of obs = 1158
LR chi2(1) = 753.54
Prob > chi2 = 0.0000
Log likelihood = -353.91719 Pseudo R2 = 0.5156
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
avg_ed | 3.909635 .2383083 16.41 0.000 3.442559 4.376711
_cons | -12.30054 .7314646 -16.82 0.000 -13.73418 -10.86689
------------------------------------------------------------------------------
lrtest full_model .
Likelihood-ratio test LR chi2(1) = 11.40
(Assumption: . nested in full_model) Prob > chi2 = 0.0007
The chi-square statistic equals 11.40, which is statistically significant. This means that the variable that was removed to produce the reduced model resulted in a model that has a significantly poorer fit, and therefore the variable should be included in the model. Now let’s take a moment to make a few comments on the code used above. For the second logit (for the reduced model), we have added if e(sample), which tells Stata to only use the cases that were included in the first model. If there were missing data on one of the variables that was dropped from the full model to make the reduced model, there would be more cases used in the reduced model. That exactly the same cases are used in both models is important because the lrtest assumes that the same cases are used in each model. The dot (.) at the end of the lrtest command is not necessary to include, but we have included it to be explicit about what is being tested. Stata "names" a model . if you have not specifically named it.
For our final example, imagine that you have a model with lots of predictors in it. You could run many variations of the model, dropping one variable at a time or groups of variables at a time. Each time that you run a model, you would use the est store command and give each model its own name. We will try a mini-example below.
* full model
logit hiqual yr_rnd avg_ed meals full
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -365.45045
Iteration 2: log likelihood = -297.5258
Iteration 3: log likelihood = -274.85521
Iteration 4: log likelihood = -270.54954
Iteration 5: log likelihood = -270.3409
Iteration 6: log likelihood = -270.34028
Logistic regression Number of obs = 1158
LR chi2(4) = 920.69
Prob > chi2 = 0.0000
Log likelihood = -270.34028 Pseudo R2 = 0.6300
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
yr_rnd | -.9703336 .3810292 -2.55 0.011 -1.717137 -.22353
avg_ed | 2.047529 .300159 6.82 0.000 1.459228 2.63583
meals | -.0725818 .0077699 -9.34 0.000 -.0878106 -.0573531
full | .0336658 .0133099 2.53 0.011 .0075788 .0597527
_cons | -6.994542 1.722563 -4.06 0.000 -10.3707 -3.61838
------------------------------------------------------------------------------
est store a
* with yr_rnd removed from the model
logit hiqual avg_ed meals full if e(sample)
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -365.50944
Iteration 2: log likelihood = -298.91372
Iteration 3: log likelihood = -277.66868
Iteration 4: log likelihood = -273.90919
Iteration 5: log likelihood = -273.75198
Iteration 6: log likelihood = -273.75163
Logistic regression Number of obs = 1158
LR chi2(3) = 913.87
Prob > chi2 = 0.0000
Log likelihood = -273.75163 Pseudo R2 = 0.6254
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
avg_ed | 2.045295 .2936238 6.97 0.000 1.469803 2.620787
meals | -.0727145 .0076311 -9.53 0.000 -.0876711 -.0577578
full | .0349739 .0132324 2.64 0.008 .0090389 .0609089
_cons | -7.199853 1.704632 -4.22 0.000 -10.54087 -3.858837
------------------------------------------------------------------------------
est store b
lrtest a b, stats
Likelihood-ratio test LR chi2(1) = 6.82
(Assumption: b nested in a) Prob > chi2 = 0.0090
------------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+----------------------------------------------------------------
b | 1158 -730.6871 -273.7516 4 555.5033 575.7211
a | 1158 -730.6871 -270.3403 5 550.6806 575.9528
------------------------------------------------------------------------------
* with yr_rnd and full removed from the model
logit hiqual avg_ed meals if e(sample)
Iteration 0: log likelihood = -730.68708
Iteration 1: log likelihood = -365.44681
Iteration 2: log likelihood = -299.2168
Iteration 3: log likelihood = -280.19401
Iteration 4: log likelihood = -277.46203
Iteration 5: log likelihood = -277.38133
Iteration 6: log likelihood = -277.38124
Logistic regression Number of obs = 1158
LR chi2(2) = 906.61
Prob > chi2 = 0.0000
Log likelihood = -277.38124 Pseudo R2 = 0.6204
------------------------------------------------------------------------------
hiqual | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
avg_ed | 1.970691 .2793051 7.06 0.000 1.423263 2.518119
meals | -.0764628 .0072617 -10.53 0.000 -.0906955 -.0622301
_cons | -3.594219 .9836834 -3.65 0.000 -5.522203 -1.666235
------------------------------------------------------------------------------
est store c
lrtest a c
Likelihood-ratio test LR chi2(2) = 14.08
(Assumption: c nested in a) Prob > chi2 = 0.0009
lrtest a b
Likelihood-ratio test LR chi2(1) = 6.82
(Assumption: b nested in a) Prob > chi2 = 0.0090
These results suggest that the variables dropped from the full model to create model c should not be dropped (LR chi2(2) = 14.08, p = 0.0009). The results of the second lrtest are similar; the variables should not be dropped. In other words, it seems that the full model is preferable.
We need to remember that a test of nested models assumes that each model is run on the same sample, in other words, exactly the same observations. The likelihood ratio test is not valid otherwise. You may not have exactly the same observations in each model if you have missing data on one or more variables. In that case, you might want to run all of the models on only those observations that are available for all models (the model with the smallest number of observations).
A note about sample size
As we have stated several times in this chapter, logistic regression uses a maximum likelihood to get the estimates of the coefficients. Many of desirable properties of maximum likelihood are found as the sample size increases. The behavior of maximum likelihood with small sample sizes is not well understood. According to Long (1997, pages 53-54), 100 is a minimum sample size, and you want *at least* 10 observations per predictor. This does not mean that if you have only one predictor you need only 10 observations. If you have categorical predictors, you may need to have more observations to avoid computational difficulties caused by empty cells. More observations are needed when the dependent variable is very lopsided; in other words, when there are very few 1’s and lots of 0’s, or vice versa. In chapter 3 of this web book is a discussion of multicollinearity. When this is present, you will need a larger sample size.
Conclusion
We realize that we have covered quite a bit of material in this chapter. Our main goals were to make you aware of 1) the similarities and differences between OLS regression and logistic regression and 2) how to interpret the output from Stata’s logit and logistic commands. We have used both a dichotomous and a continuous independent variable in the logistic regressions that we have run so far. As in OLS regression, categorical variables require special attention, which they will receive in the next chapter.