About This Presentation
- It is a broad survey of count regression models
- It is designed to demonstrate the range of analyses available for count regression models
- It is not an in-depth statistical presentation
- It is not a how-to manual that will train you in count data analysisWhy Use Count Regression Models
- Count data is common in many disciplines
- Count models can be used for rate data in many instances by using exposure
- Count data often analyzed incorrectly with OLS regression
Regression Models with Count Data Outline
- Poisson Regression
- Negative Binomial Regression
- Zero-Inflated Count Models
- Zero-inflated Poisson
- Zero-inflated Negative Binomial
- Zero-Truncated Count Models
- Zero-truncated Poisson
- Zero-truncated Negative Binomial
- Hurdle Models
- Random-effects Count Models
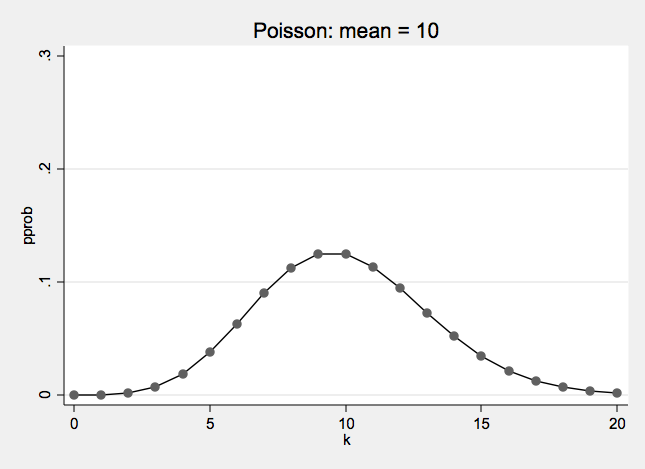
Poisson Distribution
The Poisson probability distribution.
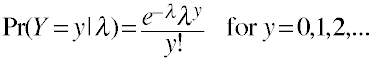
- λ is the mean or expected value of a Poisson distribution
- λ is also the variance of a Poisson distribution
- Poisson is a one parameter λ (lambda)
Likelihood function for the Poisson model.
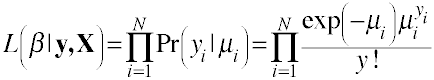

Some History of the Poisson Distribution
The Poisson distribution was first published by Siméon-Denis Poisson in 1838.

There is a famous example from a 1898 book by Ladislaus von Bortkiewicz showing that the number of soldiers killed by mule-kicks each year in the Prussian cavalry followed a Poisson distribution. The title of the book was The Law of Small Numbers.

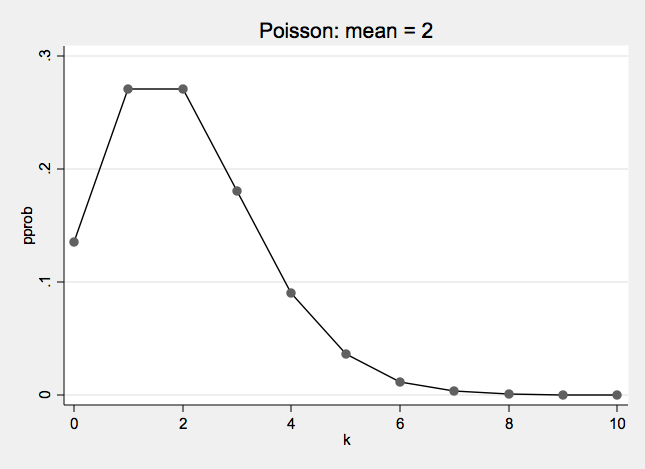
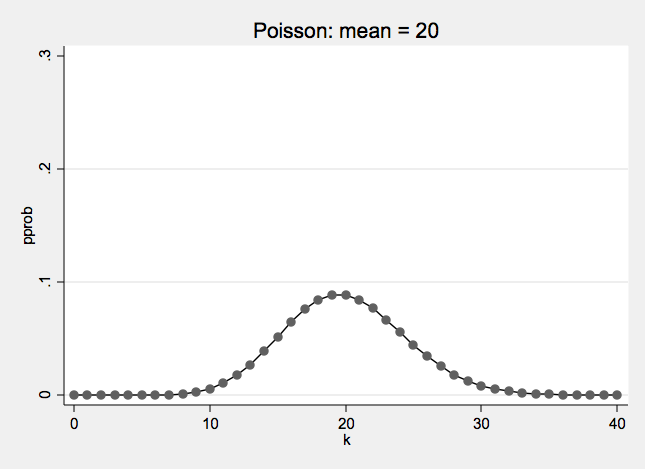
Poisson Examples
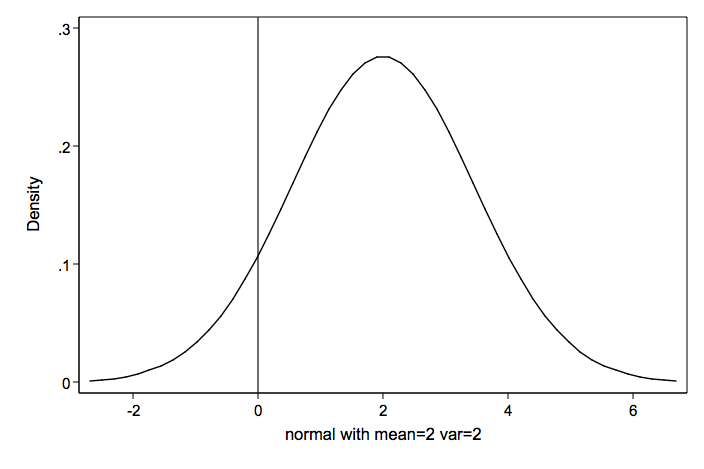
As a comparison, here is a normal distribution with the same mean and variance as the Poisson distribution above.
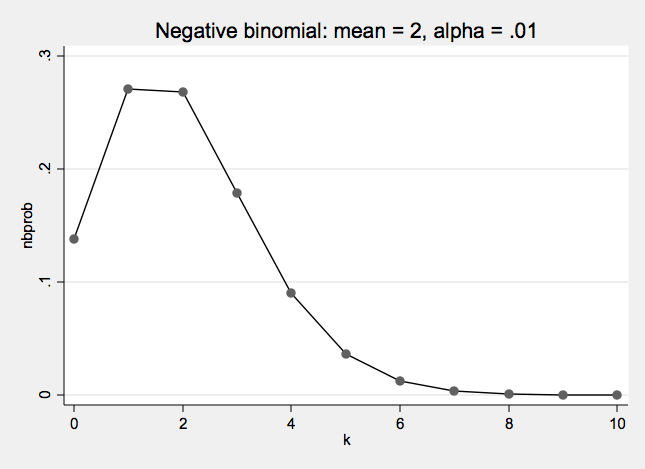
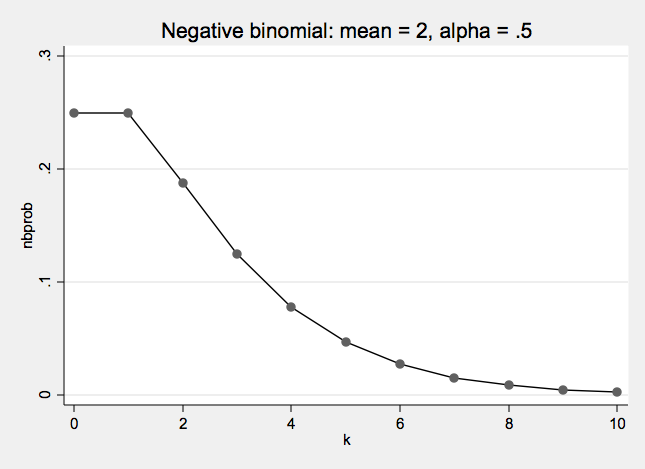
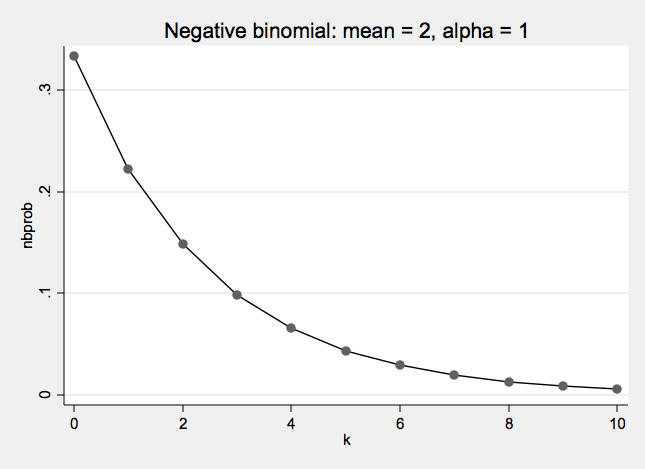
Negative Binomial Distribution One formulation of the negative binomial distribution can be used to model count data with over-dispersion.
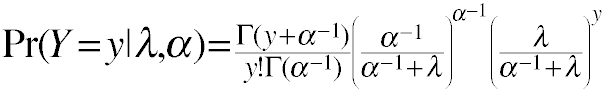
- The negative binomial distribution has two parameters: λ and α
- λ is the mean or expected value of the distribution
- α is the over dispersion parameter
- When α = 0 the negative binomial distribution is the same as a Poisson distribution
Likelihood function for the negative binomial model.
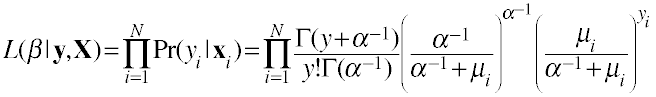

Negative Binomial Examples
Maximum Likelihood Estimation
Count models are estimated using maximum likelihood
Log likelihood:
- Computationally, the log of the likelihood function is easier to work with.
- Analysis proceeds iteratively until the log likelihood converges.
- Larger (in the closer to zero sense) log likelihoods are better.BIC:
- Schwartz’ Bayesian information criterion = -2*ln(L)+k*ln(n).
- Given any two estimated models, the model with the lower value of BIC is the one to be preferred.
- Can be used to compare different models, even models that are non-nested.
- Interpretation of absolute difference: 0-2 Weak, 2-6 Positive, 6-10 Strong, and >10 Very Strong.Sample size:
- The small sample behavior of ML estimators for count models is largely unknown.
- It is risky to use ML with samples smaller than 100.
- Samples over 500 seem adequate.
Soccer Goals Example
Number of goals scored for each game in a season (mean= 2.16 variance= 3.00)
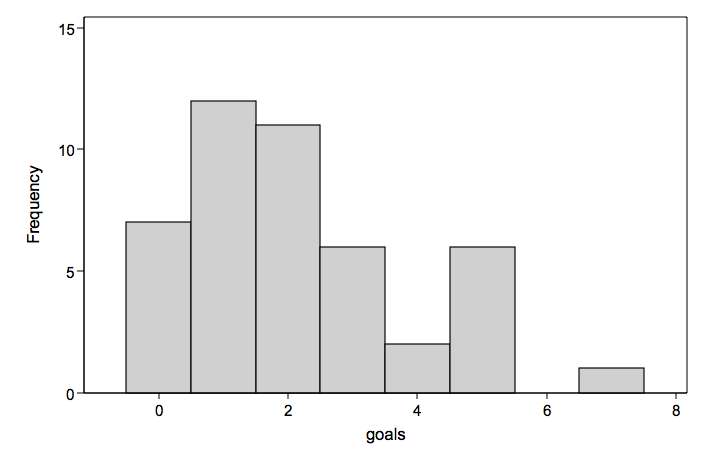
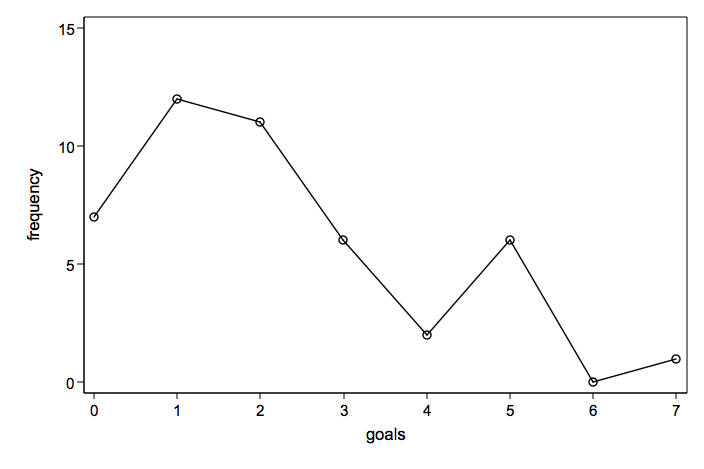
Number goals displayed as a connected line graph
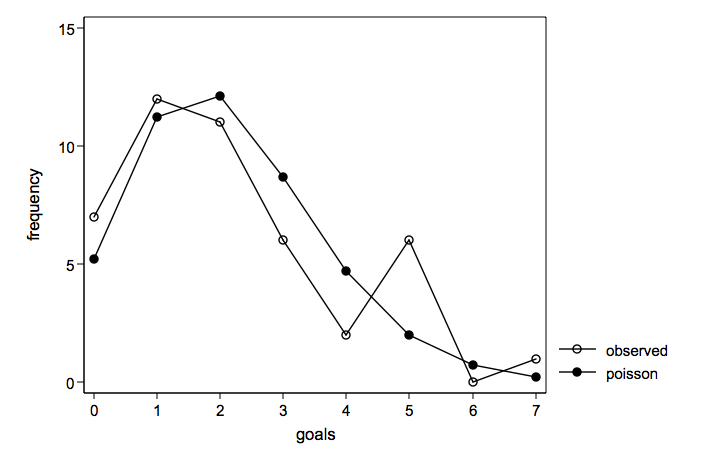
Observed number of goals overlayed with a Poisson distribution
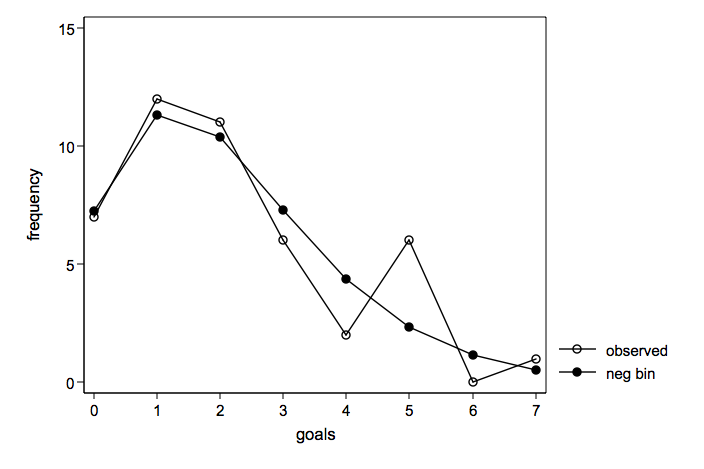
Observed number of goals overlayed with a negative binomial distribution
Exposure
Count models need some sort of mechanism to deal with the fact that counts can be made over different observation periods. For example, the number of accidents are recorded for 50 different intersections. However, the number of vehicles that pass through the intersections can vary greatly. Fifteen accidents for 30,000 vehicles is very different from 15 accidents for 1,500 vehicles. Count models account for these differences by including the log of the exposure variable in model with coefficient constrained to be one.
The use of exposure is superior in many instances to analyzing rates as response variables because it makes use of the correct probability distributions. It should be noted that exposure is used to adjust counts on the response variable and that it is possible to various kinds of rates, indexes or per capita measures as predictors.
Deaths
The response variable is the number of deaths recorded at each of five different age-group and two smoker categories. The difference in the number of patient years will be accounted for with an exposure variable pyears. Below, note that rows 1 and 10 have almost identical numbers of deaths but have very different values for patient years.
agecat smokes deaths pyears 1 1 32 52,407 2 1 104 43,248 3 1 206 28,612 4 1 186 12,663 5 1 102 5,317 1 0 2 18,790 2 0 12 10,673 3 0 28 5,710 4 0 28 2,585 5 0 31 1,462 variable | N mean variance min max -------------+-------------------------------------------------- deaths | 10 73.1 5390.767 2 206 pyears | 10 18146.7 3.16e+08 1462 52407 ----------------------------------------------------------------The predictor variables are four age-group dummy variables and a dummy variable to indicate smokers.
These data can be analyzed with either a Poisson regression model or a negative binomial regression model.
ll df BIC model -33.60015 6 81.0158 poisson -33.60014 7 83.3184 negative binomial
There is not much difference between the two models based on the log-likelihood and the BIC but the Poisson model has a slightly better BIC.
Poisson regression Number of obs = 10 LR chi2(5) = 922.93 Prob > chi2 = 0.0000 Log likelihood = -33.600153 Pseudo R2 = 0.9321 ------------------------------------------------------------------------------ deaths | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- smokes | .3545356 .1073741 3.30 0.001 .1440862 .564985 a2 | 1.484007 .1951034 7.61 0.000 1.101611 1.866403 a3 | 2.627505 .1837273 14.30 0.000 2.267406 2.987604 a4 | 3.350493 .1847992 18.13 0.000 2.988293 3.712693 a5 | 3.700096 .1922195 19.25 0.000 3.323353 4.07684 _cons | -7.919326 .1917618 -41.30 0.000 -8.295172 -7.543479 pyears | (exposure) ------------------------------------------------------------------------------
Zero-inflated Models
Zero-inflated models attempt to account for excess zeros, i.e., there is thought to be two kinds of zeros, “true zeros” and excess zeros. Zero-inflated models estimate two equations, one for the count model and one for the excess zero’s.
Fishing Example
Somehow, it seems very appropriate to discuss fish and Poisson in the same example.
Response variable: count — the number of fish caught by visitors to a state park
Predictors: child — number of children in group camper — camping one or more nights during stay (0/1) persons — number of people in group
Child is also used as the predictor of the inflated-zeros
In our example “true zeros” are obtained from people who fish but do not catch anything. The excess zeros come from those who do not fish at all. Separate equations are used to predict each kind of zero.
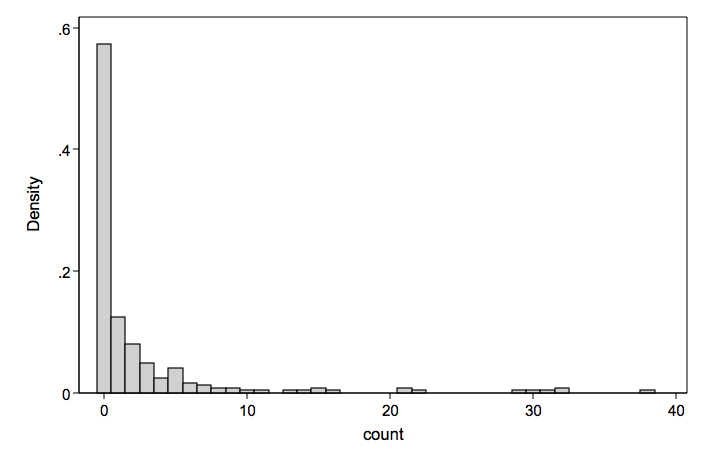
We will look at two count models and two zero-inflated models and an OLS regression for comparison.
ll df BIC model -749.3503 4 1520.754 ols -645.2568 4 1312.567 poisson -391.0271 5 809.621 negative binomial -561.5176 6 1156.116 zero-inflated poisson -384.8586 7 808.311 zero-inflated negative binomial
The results for the zero-inflated negative binomial are given below. Note this model is only marginally better than the ordinary negative binomial model and the Vuong test is not significant but the data were clearly generated by a process that leads to inflated zeros.
Zero-inflated negative binomial regression Number of obs = 248 Nonzero obs = 106 Zero obs = 142 Inflation model = logit LR chi2(3) = 69.88 Log likelihood = -384.8586 Prob > chi2 = 0.0000 ------------------------------------------------------------------------------ | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- count | child | -1.017093 .2734393 -3.72 0.000 -1.553025 -.4811623 camper | .4953317 .2320177 2.13 0.033 .0405854 .950078 persons | .9412857 .1142745 8.24 0.000 .7173118 1.16526 _cons | -1.440209 .3237543 -4.45 0.000 -2.074756 -.8056624 -------------+---------------------------------------------------------------- inflate | child | 2.857134 .7912044 3.61 0.000 1.306402 4.407866 _cons | -4.155515 1.358571 -3.06 0.002 -6.818266 -1.492765 -------------+---------------------------------------------------------------- /lnalpha | .5080559 .1945664 2.61 0.009 .1267128 .889399 -------------+---------------------------------------------------------------- alpha | 1.662057 .3233804 1.135091 2.433667 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 353.32 Pr>=chibar2 = 0.0000 Vuong test of zinb vs. standard negative binomial: z = 1.29 Pr>z = 0.0981Here are the results from the several of the other models that we can look at the differences in the output.
OLS regression Source | SS df MS Number of obs = 248 -------------+------------------------------ F( 3, 244) = 31.67 Model | 2381.37932 3 793.793107 Prob > F = 0.0000 Residual | 6116.21745 244 25.066465 R-squared = 0.2802 -------------+------------------------------ Adj R-squared = 0.2714 Total | 8497.59677 247 34.4032258 Root MSE = 5.0066 ------------------------------------------------------------------------------ count | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- child | -3.66316 .4517096 -8.11 0.000 -4.552908 -2.773412 camper | 1.803715 .6462559 2.79 0.006 .5307624 3.076667 persons | 2.958617 .3471834 8.52 0.000 2.274758 3.642476 _cons | -3.513368 .911917 -3.85 0.000 -5.309602 -1.717134 ------------------------------------------------------------------------------ Poisson regression Poisson regression Number of obs = 248 LR chi2(3) = 825.76 Prob > chi2 = 0.0000 Log likelihood = -645.25676 Pseudo R2 = 0.3902 ------------------------------------------------------------------------------ count | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- child | -1.435991 .0817147 -17.57 0.000 -1.596149 -1.275834 camper | .6581591 .0928267 7.09 0.000 .4762221 .840096 persons | .8921543 .0412052 21.65 0.000 .8113936 .972915 _cons | -1.406989 .1512168 -9.30 0.000 -1.703369 -1.11061 ------------------------------------------------------------------------------ Negative binomial regression Negative binomial regression Number of obs = 248 LR chi2(3) = 94.97 Dispersion = mean Prob > chi2 = 0.0000 Log likelihood = -391.02712 Pseudo R2 = 0.1083 ------------------------------------------------------------------------------ count | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- child | -1.663023 .1952636 -8.52 0.000 -2.045732 -1.280313 camper | .5581623 .2323451 2.40 0.016 .1027743 1.01355 persons | .9721464 .1223069 7.95 0.000 .7324293 1.211864 _cons | -1.462463 .334303 -4.37 0.000 -2.117685 -.8072411 -------------+---------------------------------------------------------------- /lnalpha | .7456885 .1585742 .4348888 1.056488 -------------+---------------------------------------------------------------- alpha | 2.107892 .3342573 1.544791 2.876253 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 508.46 Prob>=chibar2 = 0.000
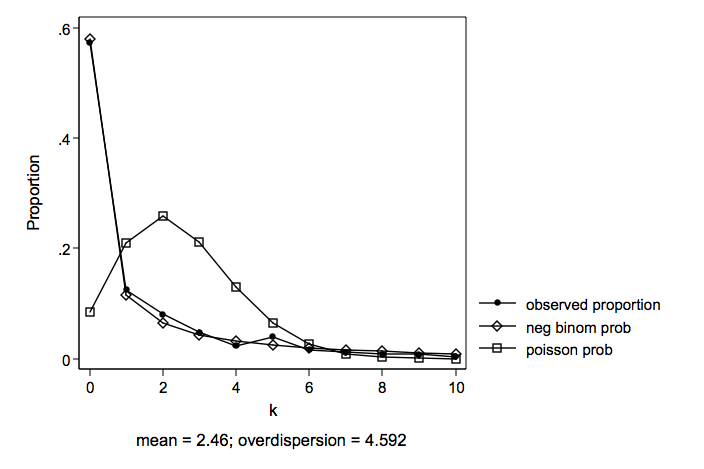
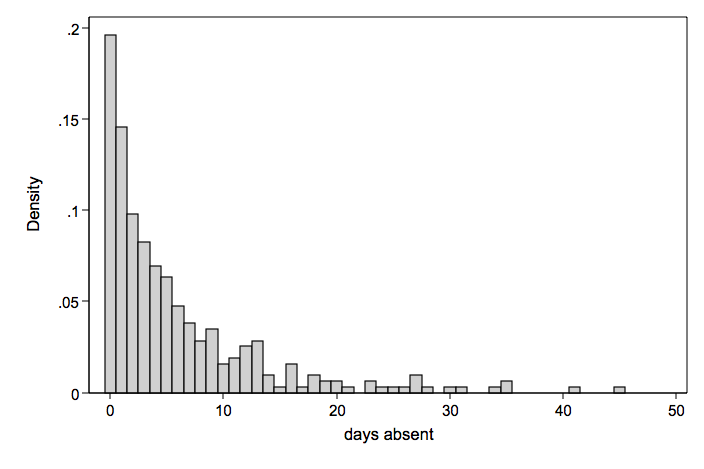
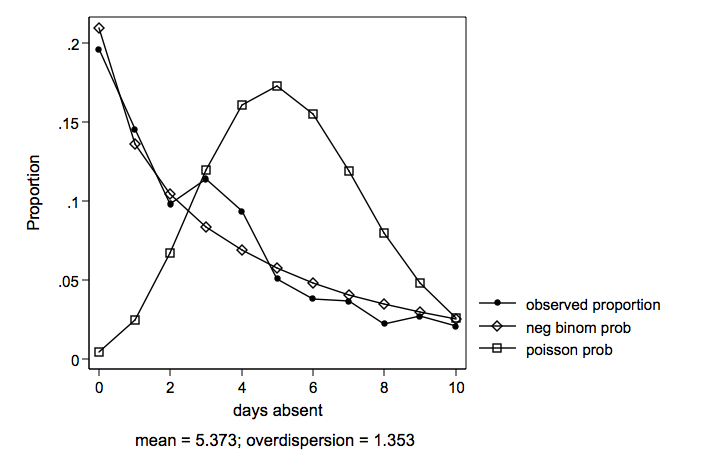
Days Absent From School
Days absent from school during one school year (mean = 5.81 variance = 55.49)
Predictors of the count variable are female, school and reading.
Several variables were tried as predictors of excess zeros for zero-inflated models. The large number of zeros in the data might seem to suggest some type of zero-inflated model. However, the zero-inflated models were not used for both empirical reasons and because there did not seem to be a reasonable way explain what kind of a process would generate excess zeros in days absent.
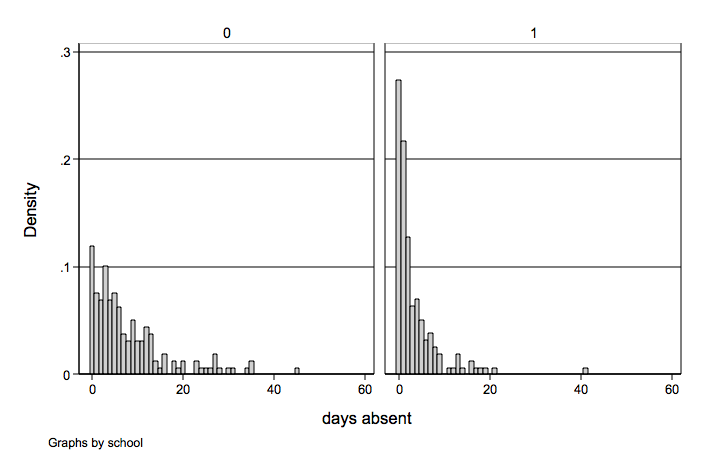
Histogram of days absent by school.
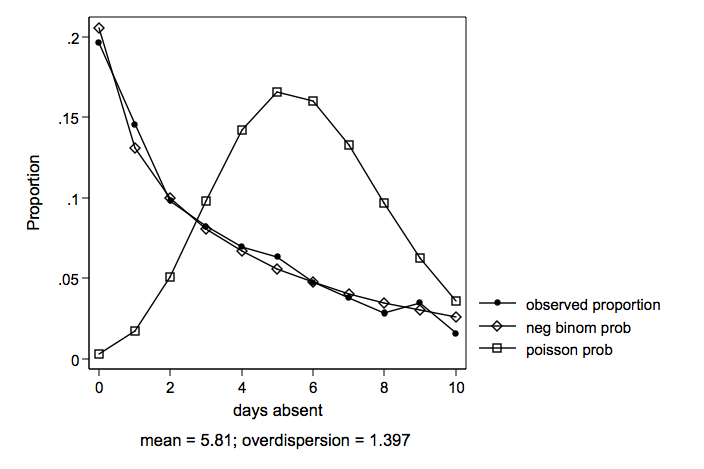
We will look at five different models, two count models, two zero-inflated count model and an ols regression thrown in for good measure.
ll df BIC model -1060.365 4 2143.75 ols regression -1435.846 3 2894.72 poisson -867.240 4 1763.26 negative binomial -1278.182 5 2590.90 zero-inflated poisson -867.200 6 1774.69 zero-inflated negative binomial
Both the negative binomial and the zero-inflated negative binomial are very close in log likelihoods and BIC’s, there’s a slight edge to the straight negative binomial due to having fewer degrees of freedom.
Negative binomial regression Number of obs = 316 LR chi2(2) = 44.02 Dispersion = mean Prob > chi2 = 0.0000 Log likelihood = -869.23382 Pseudo R2 = 0.0247 ------------------------------------------------------------------------------ daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- female | .3366034 .132156 2.55 0.011 .0775823 .5956244 school | -.8628592 .1323017 -6.52 0.000 -1.122166 -.6035526 _cons | 2.776001 .2142417 12.96 0.000 2.356094 3.195907 -------------+---------------------------------------------------------------- /lnalpha | .1568369 .0986426 -.036499 .3501728 -------------+---------------------------------------------------------------- alpha | 1.169805 .1153925 .9641591 1.419313 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 1152.21 Prob>=chibar2 = 0.000
Zero-truncated Models
There are a number of interesting situations in which the count variable cannot take on the value zero.
Take for example the response variable length of hospital stay (mean = 5.37 variance = 49.24). The predictor variables are age, hmo and died (died before discharge). Note that there are no zero counts in the data.
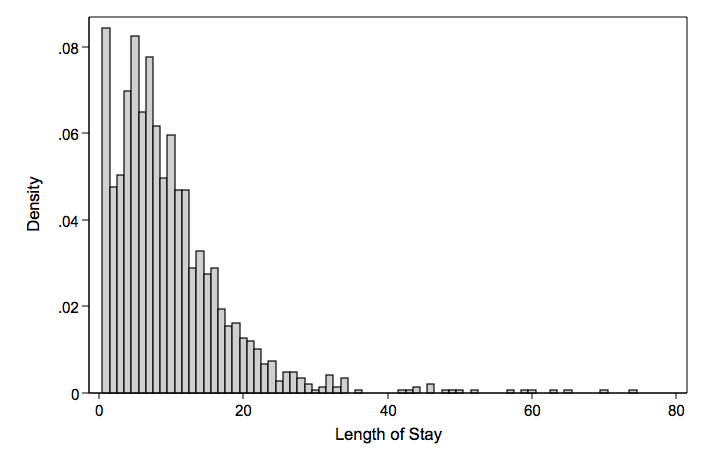
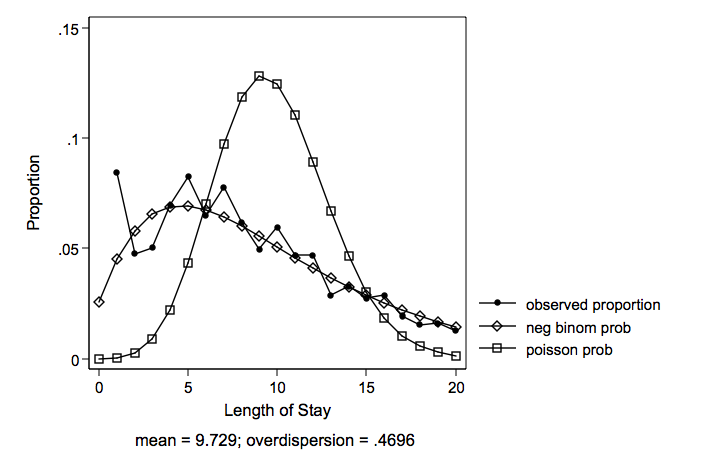
Note that both Poisson and negative binomial predict a probability for zero length of hospital stay. The negative binomial provides a closer fit to the observed than does the Poisson.
ll df BIC model -6908.799 4 13846.83 zero-truncated poisson -4755.28 5 9547.10 zero-truncated negative binomial
The results for the zero-truncated negative binomial are given below.
Zero-truncated negative binomial regression Number of obs = 1493 LR chi2(3) = 31.14 Dispersion = mean Prob > chi2 = 0.0000 Log likelihood = -4755.2796 Pseudo R2 = 0.0033 ------------------------------------------------------------------------------ stay | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- age | -.0156929 .013107 -1.20 0.231 -.0413822 .0099964 hmo | -.1470576 .0592161 -2.48 0.013 -.263119 -.0309962 died | -.2177714 .0461605 -4.72 0.000 -.3082442 -.1272985 _cons | 2.408328 .071982 33.46 0.000 2.267245 2.54941 -------------+---------------------------------------------------------------- /lnalpha | -.5686389 .0551506 -.6767321 -.4605457 -------------+---------------------------------------------------------------- alpha | .5662957 .0312316 .5082753 .6309393 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 4307.04 Prob>=chibar2 = 0.000
Hurdle Models
A hurdle model is a modified count model in which there are two processes, one generating the zeros and one generating the positive values. The two models are not constrained to be the same. The concept underlying the hurdle model is that a binomial probability model governs the binary outcome of whether a count variable has a zero or a positive value. If the value is positive, the “hurdle is crossed,” and the conditional distribution of the positive values is governed by a zero-truncated count model.
We will illustrate this model using artificially generated data with response variable y and predictors x1 and x2.
y | Freq. ------------+--------------- 0 | 315 1 | 123 2 | 138 3 | 117 4 | 88 5 | 60 6 | 35 7 | 23 8 | 24 9 | 19 10 | 16 11 | 11 12 | 10 13 | 5 14 | 1 15 | 4 16 | 1 19 | 2 21 | 2 22 | 2 26 | 1 32 | 2 34 | 1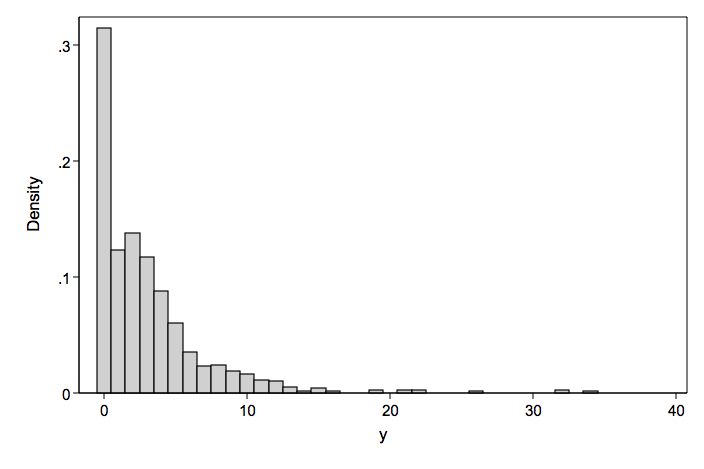
Since the count part of the model was generated using a random Poisson generator, we will look at three different Poisson based models.
ll df BIC model -2133.079 3 4286.881 poisson -1748.863 6 3539.173 zero-inflated poisson -1730.438 6 3502.322 poisson-logit hurdle
The Poisson-logit hurdle model is clearly the best choice here. The results for this model are given below
Poisson-Logit Hurdle Regression Number of obs = 1000 Wald chi2(2) = 187.13 Log likelihood = -1730.4377 Prob > chi2 = 0.0000 ------------------------------------------------------------------------------ | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- logit | x1 | 1.494141 .1092238 13.68 0.000 1.280067 1.708216 x2 | .0637035 .086461 0.74 0.461 -.105757 .233164 _cons | .9951839 .0855003 11.64 0.000 .8276064 1.162761 -------------+---------------------------------------------------------------- poisson | x1 | .1732047 .0226329 7.65 0.000 .128845 .2175644 x2 | .7216143 .0198055 36.44 0.000 .6827963 .7604324 _cons | 1.009172 .0284237 35.50 0.000 .9534629 1.064882 ------------------------------------------------------------------------------
Days Absent Clustered in Schools
We will take another look at days absent (mean = 5.37 variance = 49.24), this time obtained from 12 schools with about 50 students per school. The predictors are gender and reading. Any count model will need to account for the lack of independence within schools.
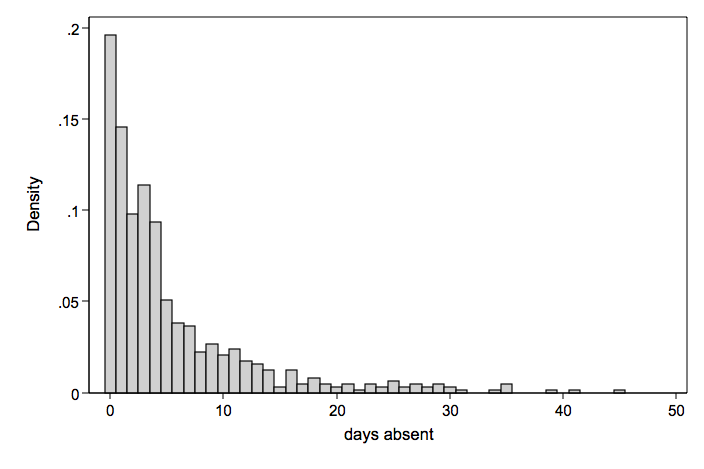
We have a number of options for analyzing these data. We can use standard poisson with cluster robust standard errors to account for within school association. Or we can use one of the random-effects models for poisson or negative binomial. These are random intercept only models.
ll df BIC model -2938.653 3 5896.653 poisson with cluster robust standard errors -1718.321 4 3462.437 negative binomial with cluster robust standard errors -2718.767 4 5463.33 random-effects poisson w/ gaussian random effects -2718.864 4 5463.523 random-effects poisson w/ gamma random effects -1696.797 5 3425.838 random-effects negative binomial w/ beta random effects
The random-effects negative binomial has the best log likelihood and BIC. The results of the model are given below.
Random-effects negative binomial regression Number of obs = 632 Group variable (i): sid Number of groups = 12 Random effects u_i ~ Beta Obs per group: min = 51 avg = 52.7 max = 53 Wald chi2(2) = 36.14 Log likelihood = -1696.7966 Prob > chi2 = 0.0000 ------------------------------------------------------------------------------ daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- female | .3587537 .0788313 4.55 0.000 .2042472 .5132602 reading | -.0102389 .0022909 -4.47 0.000 -.0147289 -.0057489 _cons | .1944149 .131354 1.48 0.139 -.0630343 .451864 -------------+---------------------------------------------------------------- /ln_r | 2.260673 .4859689 1.308192 3.213155 /ln_s | 3.922436 .5105199 2.921835 4.923037 -------------+---------------------------------------------------------------- r | 9.589543 4.66022 3.699478 24.85738 s | 50.52336 25.79318 18.57535 137.4193 ------------------------------------------------------------------------------ Likelihood-ratio test vs. pooled: chibar2(01) = 32.25 Prob>=chibar2 = 0.000
Summary of Count Regression Models
- Poisson regression model
- Negative binomial regression model
- Zero-inflated poisson model
- Zero-inflated negative binomial model
- Zero-truncated poisson model
- Zero-truncated negative binomial model
- Hurdle models
- Random-effects count models
Some Stata Specific Information
Here are the Stata commands for selected models shown above:
poisson regression with exposure, deaths (also see DAE page): . poisson deaths smokes a2 a3 a4 a5, exposure(pyears) zero-inflated negative binomial, fish (also see DAE page): . zinb count child camper persons, inflate(child) vuong zip negative binomial regression, days absent (also see DAE page): . nbreg daysabs female school Zero-truncated negative binomial regression, length of hosptial stay (also see DAE page): . ztnb stay age hmo died Poisson-Logit Hurdle Regression, artifical data . hplogit y x1 x2 negative binomial regression with cluster robust standard errors, days absent: . nbreg daysabs female reading, cluster(sid) random effects negative binomial, days absent: . xtnbreg daysabs female reading, i(sid)
References Here are some places to read more about regression models with count data.
Agresti, A. (2001) Categorical Data Analysis (2nd ed). New York: Wiley.
Agresti, A. (1996) An Introduction to Categorical Data Analysis. New York: Wiley.
Long, S. J. (1997) Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: SAGE Publications, Inc.
Long, S. J. & Freese, J. (2001) Regression Models for Categorical Dependent Variables using Stata. College Station, TX: Stata Press.
