The purpose of this workshop is to explore some issues in the analysis of survey data using Stata 13. Before we begin, you will want to be sure that your copy of Stata is up-to-date. To do this, please type
update all
in the Stata command window and follow any instructions given. These updates include not only fixes to known bugs, but also add some new features that may be useful. I am using Stata 13.1.
Before we begin looking at examples in Stata, we will quickly review some basic issues and concepts in survey data analysis.
NOTE: Most of the commands in this seminar will work with Stata 12.
Why do we need survey data analysis software?
Regular statistical software (that is not designed for survey data) analyzes data as if the data were collected using simple random sampling. For experimental and quasi-experimental designs, this is exactly what we want. However, very few surveys use a simple random sample to collect data. Not only is it nearly impossible to do so, but it is not as efficient (either financially and statistically) as other sampling methods. When any sampling method other than simple random sampling is used, we usually need to use survey data analysis software to take into account the differences between the design that was used to collect the data and simple random sampling. This is because the sampling design affects both the calculation of the point estimates and the standard errors of those estimates. If you ignore the sampling design, e.g., if you assume simple random sampling when another type of sampling design was used, both the point estimates and their standard errors will likely be calculated incorrectly. The sampling weight will affect the calculation of the point estimate, and the stratification and/or clustering will affect the calculation of the standard errors. Ignoring the clustering will likely lead to standard errors that are underestimated, possibly leading to results that seem to be statistically significant, when in fact, they are not. The difference in point estimates and standard errors obtained using non-survey software and survey software with the design properly specified will vary from data set to data set, and even between analyses using the same data set. While it may be possible to get reasonably accurate results using non-survey software, there is no practical way to know beforehand how far off the results from non-survey software will be.
Sampling designs
Most people do not conduct their own surveys. Rather, they use survey data that some agency or company collected and made available to the public. The documentation must be read carefully to find out what kind of sampling design was used to collect the data. This is very important because many of the estimates and standard errors are calculated differently for the different sampling designs. Hence, if you mis-specify the sampling design, the point estimates and standard errors will likely be wrong.
Below are some common features of many sampling designs.
Sampling weights: There are several types of weights that can be associated with a survey. Perhaps the most common is the sampling weight. A sampling weight is a probability weight that has had one or more adjustments made to it. Both a sampling weight and a probability weight are used to weight the sample back to the population from which the sample was drawn. By definition, a probability weight is the inverse of the probability of being included in the sample due to the sampling design (except for a certainty PSU, see below). The probability weight, called a pweight in Stata, is calculated as N/n, where N = the number of elements in the population and n = the number of elements in the sample. For example, if a population has 10 elements and 3 are sampled at random with replacement, then the probability weight would be 10/3 = 3.33. In a two-stage design, the probability weight is calculated as f1f2, which means that the inverse of the sampling fraction for the first stage is multiplied by the inverse of the sampling fraction for the second stage. Under many sampling plans, the sum of the probability weights will equal the population total.
While many textbooks will end their discussion of probability weights here, this definition does not fully describe the sampling weights that are included with actual survey data sets. Rather, the sampling weight, which is sometimes called a "final weight," starts with the inverse of the sampling fraction, but then incorporates several other values, such as corrections for unit non-response, errors in the sampling frame (sometimes called non-coverage), and poststratification. Because these other values are included in the probability weight that is included with the data set, it is often inadvisable to modify the sampling weights, such as trying to standardize them for a particular variable, e.g., age.
PSU: This is the primary sampling unit. This is the first unit that is sampled in the design. For example, school districts from California may be sampled and then schools within districts may be sampled. The school district would be the PSU. If states from the US were sampled, and then school districts from within each state, and then schools from within each district, then states would be the PSU. One does not need to use the same sampling method at all levels of sampling. For example, probability-proportional-to-size sampling may be used at level 1 (to select states), while cluster sampling is used at level 2 (to select school districts). In the case of a simple random sample, the PSUs and the elementary units are the same. In general, accounting for the clustering in the data (i.e., using the PSUs), will increase the standard errors of the point estimates. Conversely, ignoring the PSUs will tend to yield standard errors that are too small, leading to false positives when doing significance tests.
Strata: Stratification is a method of breaking up the population into different groups, often by demographic variables such as gender, race or SES. Each element in the population must belong to one, and only one, strata. Once the strata have been defined, samples are taken from each stratum as if it were independent of all of the other strata. For example, if a sample is to be stratified on gender, men and women would be sampled independently of one another. This means that the probability weights for men will likely be different from the probability weights for the women. In most cases, you need to have two or more PSUs in each stratum. The purpose of stratification is to reduce the standard error of the estimates, and stratification works most effectively when the variance of the dependent variable is smaller within the strata than in the sample as a whole.
FPC: This is the finite population correction. This is used when the sampling fraction (the number of elements or respondents sampled relative to the population) becomes large. The FPC is used in the calculation of the standard error of the estimate. If the value of the FPC is close to 1, it will have little impact and can be safely ignored. In some survey data analysis programs, such as SUDAAN, this information will be needed if you specify that the data were collected without replacement (see below for a definition of "without replacement"). The formula for calculating the FPC is ((N-n)/(N-1))1/2, where N is the number of elements in the population and n is the number of elements in the sample. To see the impact of the FPC for samples of various proportions, suppose that you had a population of 10,000 elements.
Sample size (n) FPC 1 1.0000 10 .9995 100 .9950 500 .9747 1000 .9487 5000 .7071 9000 .3162
Replicate weights: Replicate weights are a series of weight variables that are used to correct the standard errors for the sampling plan. They serve the same function as the PSU and strata variables (which are used a Taylor series linearization) to correct the standard errors of the estimates for the sampling design. Many public use data sets are now being released with replicate weights instead of PSUs and strata in an effort to more securely protect the identity of the respondents. In theory, the same standard errors will be obtained using either the PSU and strata or the replicate weights. There are different ways of creating replicate weights; the method used is determined by the sampling plan. The most common are balanced repeated and jackknife replicate weights. You will need to read the documentation for the survey data set carefully to learn what type of replicate weight is included in the data set; specifying the wrong type of replicate weight will likely lead to incorrect standard errors. For more information on replicate weights, please see Stata Library: Replicate Weights and Appendix D of the WesVar Manual by Westat, Inc. Several statistical packages, including Stata, SAS, SUDAAN, WesVar and R, allow the use of replicate weights.
Consequences of not using the design elements
Sampling design elements include the sampling weights, post-stratification weights (if provided), PSUs, strata, and replicate weights. Rarely are all of these elements included in a single public-use data set. However, ignoring the design elements that are included can often lead to inaccurate point estimates and/or inaccurate standard errors.
Sampling with and without replacement
Most samples collected in the real world are collected "without replacement". This means that once a respondent has been selected to be in the sample and has participated in the survey, that particular respondent cannot be selected again to be in the sample. Many of the calculations change depending on if a sample is collected with or without replacement. Hence, programs like SUDAAN request that you specify if a survey sampling design was implemented with our without replacement, and an FPC is used if sampling without replacement is used, even if the value of the FPC is very close to one.
Examples
For the examples in this workshop, we will use the data set from NHANES 2011-2012. The data set and documentation can be downloaded from the NHANES web site. The data files can be downloaded as SAS.xpt files. Files in this format can be read directly into Stata using the fdause command.
Reading the documentation
The first step in analyzing any survey data set is to read the documentation. With many of the public use data sets, the documentation can be quite extensive and sometimes even intimidating. Instead of trying to read the documentation "cover to cover", there are some parts you will want to focus on. First, read the Introduction. This is usually an "easy read" and will orient you to the survey. There is usually a section or chapter called something like "Sample Design and Analysis Guidelines", "Variance Estimation", etc. This is the part that tells you about the design elements included with the survey and how to use them. Some even give example code. If multiple sampling weights have been included in the data set, there will be some instruction about when to use which one. If there is a section or chapter on missing data or imputation, please read that. This will tell you how missing data were handled. You should also read any documentation regarding the specific variables that you intend to use. As we will see little later on, we will need to look at the documentation to get the value labels for the variables. This is especially important because some of the values are actually missing data codes, and you need to do something so that Stata doesn’t treat those as valid values (or you will get some very "interesting" means, totals, etc.).
Getting the data into Stata
The following commands can be used to open the NHANES data in Stata and save them in Stata format. I have also sorted the data before saving them (because I will merge the files), but this is not technically necessary.
* demographics clear fdause "D:DataSeminarsApplied Survey Stata 13demo_g.xpt" sort seqn save "D:DataSeminarsApplied Survey Stata 13demo_g", replace
The do-file that imports the data, merges the files and recodes the variables can be found here. More variables are recoded in the do-file than are used in this presentation.
The variables
We will use about a dozen different variables in the examples in this workshop. Below is a brief summary of them. Some of the variables have been recoded to be binary variables (values of 2 recoded to a value of 0). The count of missing observations includes values truly missing as well as refused and don’t know.
ridageyr – Age in years at exam – recoded; range of values: 0 – 79 are actual values, 80 = 80+ years of age
pad630 – How much time do you spend doing moderate-intensity activities on a type work day?; range of values: 10-960, 7053 missing observations
hsq496 – During the past 30 days, for about how many days have you felt worried, tense or anxious?; range of values: 0-30; 3073 missing observations
female – Recode of the variable riagendr; 0 = male, 1 = female; no missing observations
dmdborn4 – Country of birth; 1 = born in the United States, 0 = otherwise; 5 missing observations
dmdmartl – Marital status; 1 = married, 2 = widowed, 3 = divorced, 4 = separated, 5 = never married, 6 = living with partner; 4203 missing observations
dmdeduc2 – Education level of adults aged 20+ years; 1 = less than 9th grade, 2 = 9-11th grade, 3 = high school graduate, GED or equivalent, 4 = some college or AA degree, 5 = college graduate or above; 4201 missing observations
pad675 – How much time do you spend doing moderate-intensity sports, fitness, or recreation activities on a typical day?; range of values: 10-600; 6220 missing observations
hsq571 – During the past 12 months, have you donated blood?; 0 = no, 1 = yes; 3673 missing observations
pad680 – How much time do you usually spend sitting on a typical day?; range of values: 0-1380; 2365 missing observations
paq665 – Do you do any moderate-intensity sports, fitness or recreational activities that cause a small increase in breathing or heart rate at least 10 minutes continually?; 0 = no, 1 = yes; 2329 missing observations
hsd010 – Would you say that your general health is…; 1 = excellent, 2 = very good, 3 = good, 4 = fair, 5 = poor; 3064 missing observations
The svyset command
Before we can start our analyses, we need to issue the svyset command. The svyset command tells Stata about the design elements in the survey. Once this command has been issued, all you need to do for your analyses is use the svy: prefix before each command. Because the 2011-2012 NHANES data were released with a sampling weight (wtint2yr), a PSU variable (sdmvpsu) and a strata variable (sdmvstra), we will use these our svyset command. The svyset command looks like this:
use "D:DataSeminarsApplied Survey Stata 13nhanes2012_merged", clear svyset sdmvpsu [pw = wtint2yr], strata(sdmvstra) singleunit(centered)pweight: wtint2yr VCE: linearized Single unit: centered Strata 1: sdmvstra SU 1: sdmvpsu FPC 1: <zero>
The singleunit option was added in Stata 10. This option allows for different ways of handling a single PSU in a stratum. If you use the default option, missing, then you will get no standard errors when Stata encounters a single PSU in a stratum. This can happen as a result of missing data or running an analysis on a subpopulation. There are three other options. One is certainty, meaning that the singleton PSUs be treated as certainty PSUs; certainty PSUs are PSUs that were selected into the sample with a probability of 1 (in other words, these PSUs were certain to be in the sample) and do not contribute to the standard error. The scaled option gives a scaled version of the certainty option. The scaling factor comes from using the average of the variances from the strata with multiple sampling units for each stratum with one PSU. The centered option centers strata with one sampling unit at the grand mean instead of the stratum mean. Now that we have issued the svyset command, we can use the svydescribe command to get information on the strata and PSUs.
svydescribeSurvey: Describing stage 1 sampling units pweight: wtint2yr VCE: linearized Single unit: centered Strata 1: sdmvstra SU 1: sdmvpsu FPC 1: <zero> #Obs per Unit ---------------------------- Stratum #Units #Obs min mean max -------- -------- -------- -------- -------- -------- 90 3 862 233 287.3 351 91 3 998 309 332.7 356 92 3 875 244 291.7 328 93 2 602 276 301.0 326 94 2 688 322 344.0 366 95 2 722 348 361.0 374 96 2 676 336 338.0 340 97 2 608 292 304.0 316 98 2 708 320 354.0 388 99 2 682 320 341.0 362 100 2 700 343 350.0 357 101 2 715 357 357.5 358 102 2 624 270 312.0 354 103 2 296 140 148.0 156 -------- -------- -------- -------- -------- -------- 14 31 9756 140 314.7 388
The output above tells us that there are 14 strata with two or three PSUs in each. There are 31 PSUs. There are a different number of observations in each PSU and in each strata. There are a minimum of140 observations, a maximum of 388 observations and an average of 315 observations in the PSUs.
Descriptive statistics
We will start by calculating some descriptive statistics of some of the continuous variables. We can use the svy: mean command to get the mean of continuous variables, and we can follow that command with the estat sd command to get the standard deviation or variance of the variable.
svy: mean ridageyr
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr | 37.18519 .6964767 35.71576 38.65463
--------------------------------------------------------------
estat sd
-------------------------------------
| Mean Std. Dev.
-------------+-----------------------
ridageyr | 37.18519 22.36971
-------------------------------------
estat sd, var
-------------------------------------
| Mean Variance
-------------+-----------------------
ridageyr | 37.18519 500.4039
-------------------------------------
svy: mean pad630
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 2054
Number of PSUs = 31 Population size = 88768571
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pad630 | 139.8874 5.57906 128.1166 151.6582
--------------------------------------------------------------
svy: mean hsq496
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 5883
Number of PSUs = 31 Population size = 225667462
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
hsq496 | 5.383908 .1899507 4.983147 5.784669
--------------------------------------------------------------
Notice that a different number of observations were used in each analysis. This is important, because if you use these three variables in the same call to svy: mean, you will get different estimates of the means for each of the variables. This is because both pad630 and hsq496 have missing values. However, these variables are not missing on the same observations: Both pad630 and hsq496 are missing on the same 3666 observations, but pad630 has missing values on an additional 4036 observations, and hsq496 has missing values on 207 observations. There are only 1847 observations that have valid values for all three variables, and those are used in the calculations of the means when all of the variables are used in the same call to svy: mean.
svy: mean ridageyr pad630 hsq496
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 1847
Number of PSUs = 31 Population size = 81681482
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr | 41.97793 .8211706 40.24541 43.71045
pad630 | 139.7228 5.713696 127.668 151.7777
hsq496 | 5.37395 .2781225 4.787162 5.960737
--------------------------------------------------------------
Let’s get some descriptive statistics on some of the binary variables, such as female and dmdborn4.
svy: mean female
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
female | .5119524 .0064398 .4983657 .5255392
--------------------------------------------------------------
estat sd
-------------------------------------
| Mean Std. Dev.
-------------+-----------------------
female | .5119524 .4998827
-------------------------------------
svy: mean dmdborn4
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9751
Number of PSUs = 31 Population size = 306485936
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
dmdborn4 | .8499362 .0157561 .8166938 .8831787
--------------------------------------------------------------
estat sd
-------------------------------------
| Mean Std. Dev.
-------------+-----------------------
dmdborn4 | .8499362 .3571522
-------------------------------------
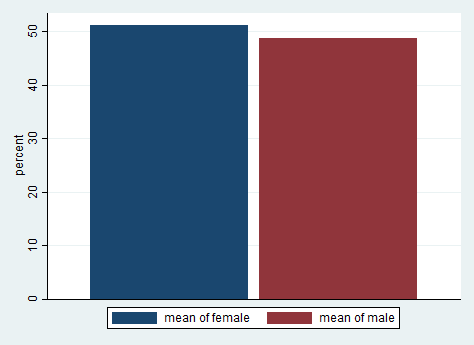
Taking the mean of a variable that is coded 0/1 gives the proportion of 1s. The output above indicates that approximately 51.2% of the observations in our data set are from females; 84.99% of respondents were born in the United States.
Of course, the svy: tab command can also be used with binary variables. The proportion of .512 matches the .5119524 that we found with the svy: mean command.
svy: tab female
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
-----------------------
RECODE of |
riagendr |
(Gender) | proportions
----------+------------
male | .488
female | .512
|
Total | 1
-----------------------
Key: proportions = cell proportions
By default, svy: tab gives proportions. If you would prefer to see the actual counts, you will need to use the count option. Oftentimes, the counts are too large for the display space in the table, so other options, such cellwidth and format need to be used to display the counts. The missing option is often useful if the variable has any missing values (the variable female does not).
svy: tab female, missing count cellwidth(15) format(%15.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
---------------------------
RECODE of |
riagendr |
(Gender) | count
----------+----------------
male | 149630839
female | 156959842
|
Total | 306590681
---------------------------
Key: count = weighted counts
svy: tab female dmdborn4, missing count cellwidth(15) format(%15.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
------------------------------------------------------------------------------
RECODE of |
riagendr | Country of birth - recode
(Gender) | born elsewhere born in US . Total
----------+-------------------------------------------------------------------
male | 22449131 127102676 79032 149630839
female | 23543299 133390830 25713 156959842
|
Total | 45992430 260493506 104745 306590681
------------------------------------------------------------------------------
Key: weighted counts
Pearson:
Uncorrected chi2(2) = 0.9477
Design-based F(1.78, 30.34) = 0.5244 P = 0.5769
Using the col option with svy: tab will give the column proportions. As you can see, the values in the column "Total" are the same as those from svy: tab female.
svy: tab female dmdborn4, col
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 9751
Number of PSUs = 31 Population size = 306485936
Design df = 17
----------------------------------------
RECODE of |
riagendr | Country of birth - recode
(Gender) | born els born in Total
----------+-----------------------------
male | .4881 .4879 .488
female | .5119 .5121 .512
|
Total | 1 1 1
----------------------------------------
Key: column proportions
Pearson:
Uncorrected chi2(1) = 0.0002
Design-based F(1, 17) = 0.0002 P = 0.9891
Of course, the svy: proportion command can also be used to get proportions.
svy: proportion female
(running proportion on estimation sample)
Survey: Proportion estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
--------------------------------------------------------------
| Linearized
| Proportion Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
female |
male | .4880476 .0064398 .474473 .5016398
female | .5119524 .0064398 .4983602 .525527
--------------------------------------------------------------
Using the estat command after the svy: mean command also allows you to get the design effects, misspecification effects, unweighted and weighted sample sizes, or the coefficient of variation. The Deff and the Deft are types of design effects, which tell you about the efficiency of your sample. The Deff is a ratio of two variances. In the numerator we have the variance estimate from the current sample (including all of its design elements), and in the denominator we have the variance from a hypothetical sample of the same size drawn as an SRS. In other words, the Deff tells you how efficient your sample is compared to an SRS of equal size. If the Deff is less than 1, your sample is more efficient than SRS; usually the Deff is greater than 1. The Deft is the ratio of two standard error estimates. Again, the numerator is the standard error estimate from the current sample. The denominator is a hypothetical SRS (with replacement) standard error from a sample of the same size as the current sample. You can also use the meff and the meft option to get the misspecification effects. Misspecification effects are a ratio of the variance estimate from the current analysis to a hypothetical variance estimated from a misspecified model. Please see the Stata documentation for more details on how these are calculated. The coefficient of variation is the ratio of the standard error to the mean, multiplied by 100% (see page 33 of the Stata 13 svy manual). It is an indication of the variability relative to the mean in the population and is not affected by the unit of measurement of the variable.
svy: mean ridageyr (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 9756 Number of PSUs = 31 Population size = 306590681 Design df = 17 -------------------------------------------------------------- | Linearized | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ ridageyr | 37.18519 .6964767 35.71576 38.65463 -------------------------------------------------------------- estat effects ---------------------------------------------------------- | Linearized | Mean Std. Err. DEFF DEFT -------------+-------------------------------------------- ridageyr | 37.18519 .6964767 9.45724 3.07526 ---------------------------------------------------------- estat effects, deff deft meff meft ------------------------------------------------------------------------------ | Linearized | Mean Std. Err. DEFF DEFT MEFF MEFT -------------+---------------------------------------------------------------- ridageyr | 37.18519 .6964767 9.45724 3.07526 7.83352 2.79884 ------------------------------------------------------------------------------ estat size ---------------------------------------------------------------------- | Linearized | Mean Std. Err. Obs Size -------------+-------------------------------------------------------- ridageyr | 37.18519 .6964767 9756 306590680.995 ---------------------------------------------------------------------- estat cv ------------------------------------------------ | Linearized | Mean Std. Err. CV (%) -------------+---------------------------------- ridageyr | 37.18519 .6964767 1.87299 ------------------------------------------------display (.6964767/37.18519)*100 1.8729949
Analysis of subpopulations
Before we continue with our descriptive statistics, we should pause to discuss the analysis of subpopulations. The analysis of subpopulations is one place where survey data and experimental data are quite different. If you have data from an experiment (or quasi-experiment), and you want to analyze the responses from, say, just the women, or just people over age 50, you can just delete the unwanted cases from the data set or use the by: prefix. Survey data are different. With survey data, you (almost) never get to delete any cases from the data set, even if you will never use them in any of your analyses. Because of the way the by: prefix works, you usually don’t use it with survey data either. Instead, Stata has provided two options that allow you to correctly analyze subpopulations of your survey data. These options are subpop and over. The subpop option is sort of like deleting unwanted cases (without really deleting them, of course), and the over option is very similar to by: processing. We will start with some examples of the subpop option.
First, however, let’s take a second to see why deleting cases from a survey data set can be so problematic. If the data set is subset (meaning that observations not to be included in the subpopulation are deleted from the data set), the standard errors of the estimates cannot be calculated correctly. When the subpopulation option(s) is used, only the cases defined by the subpopulation are used in the calculation of the estimate, but all cases are used in the calculation of the standard errors. For more information on this issue, please see Sampling Techniques, Third Edition by William G. Cochran (1977) and Small Area Estimation by J. N. K. Rao (2003). Also, if you look in the Stata 13 svy manual, you will find an entire section (pages 58-63) dedicated to the analysis of subpopulations. The formulas for using both if and subpop are given, along with an explanation of how they are different. If you look at the help for any svy: command, you will see the same warning:
Warning: Use of if or in restrictions will not produce correct variance
estimates for subpopulations in many cases. To compute estimates for
subpopulations, use the subpop() option. The full specification for subpop()
is
subpop([varname] [if])
The subpop option on the svy: prefix is used with binary variables. (Technically, all cases coded as not 0 and not missing are part of the subpopulation; this means that if your subpopulation variable has values of 1 and 2, all of the observations will be included in the subpopulation unless you use a different syntax.) You may need to create a binary variable (using the generate command) in which all of the observations be to included in the subpopulation are coded as 1 and all other observations are coded as 0. For our example, we will use the variable female for our subpopulation variable, so that only females will be included in calculation of the point estimate.
svy: mean ridageyr
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr | 37.18519 .6964767 35.71576 38.65463
--------------------------------------------------------------
svy, subpop(female): mean ridageyr
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Subpop. no. obs = 4900
Subpop. size = 156959842
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr | 38.09657 .6713502 36.68014 39.51299
--------------------------------------------------------------
To get the mean for the males, we can specify the subpopulation as the variable female not equal to 1 (meaning the observations that are coded 0).
svy, subpop(if female != 1): mean ridageyr
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Subpop. no. obs = 4856
Subpop. size = 149630839
Design df = 17
--------------------------------------------------------------
| Linearized
| Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr | 36.22918 .8431945 34.4502 38.00817
--------------------------------------------------------------
We can also use the over option, which will give the results for each level of the categorical variable listed. The over option is available only for svy: mean, svy: proportion, svy: ratio and svy: total.
svy, over(female): mean ridageyr
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 9756
Number of PSUs = 31 Population size = 306590681
Design df = 17
male: female = male
female: female = female
--------------------------------------------------------------
| Linearized
Over | Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
ridageyr |
male | 36.22918 .8431945 34.4502 38.00817
female | 38.09657 .6713502 36.68014 39.51299
--------------------------------------------------------------
We can include more than one variable with the over option; this will give us results for every combination of the variables listed.
svy, over(dmdmartl female): mean pad630
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 1705
Number of PSUs = 31 Population size = 77846933
Design df = 17
Over: dmdmartl female
_subpop_1: married male
_subpop_2: married female
_subpop_3: widowed male
_subpop_4: widowed female
_subpop_5: divorced male
_subpop_6: divorced female
_subpop_7: separated male
_subpop_8: separated female
_subpop_9: never married male
_subpop_10: never married female
_subpop_11: living with partner male
_subpop_12: living with partner female
--------------------------------------------------------------
| Linearized
Over | Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pad630 |
_subpop_1 | 156.6941 8.765612 138.2002 175.1879
_subpop_2 | 118.6255 9.590405 98.39152 138.8595
_subpop_3 | 132.6111 20.77576 88.77813 176.4442
_subpop_4 | 120.9569 11.10439 97.52869 144.3851
_subpop_5 | 209.423 27.28619 151.8541 266.9918
_subpop_6 | 124.6343 15.50591 91.91973 157.3489
_subpop_7 | 187.9685 38.86106 105.9789 269.9582
_subpop_8 | 200.9333 52.49986 90.16828 311.6983
_subpop_9 | 146.4231 12.35329 120.3599 172.4862
_subpop_10 | 131.7091 13.30558 103.6368 159.7814
_subpop_11 | 201.422 13.41895 173.1105 229.7335
_subpop_12 | 122.5736 14.88511 91.16879 153.9785
--------------------------------------------------------------
We can also use the subpop option and the over option together. In the example below, we get the mean of pad630 for females in each combination of dmdmart1 and dmdecuc2 (30 levels).
svy, subpop(female): mean pad630, over(dmdmartl dmdeduc2)
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 14 Number of obs = 5619
Number of PSUs = 31 Population size = 185989071
Subpop. no. obs = 763
Subpop. size = 36358232.8
Design df = 17
Over: dmdmartl dmdeduc2
_subpop_1: married less than 9th grade
_subpop_2: married no hs diploma
_subpop_3: married hs grad or GED
_subpop_4: married some college or AA degre
_subpop_5: married college grad or above
_subpop_6: widowed less than 9th grade
_subpop_7: widowed no hs diploma
_subpop_8: widowed hs grad or GED
_subpop_9: widowed some college or AA degre
_subpop_10: widowed college grad or above
_subpop_11: divorced less than 9th grade
_subpop_12: divorced no hs diploma
_subpop_13: divorced hs grad or GED
_subpop_14: divorced some college or AA degr
_subpop_15: divorced college grad or above
_subpop_16: separated less than 9th grade
_subpop_17: separated no hs diploma
_subpop_18: separated hs grad or GED
_subpop_19: separated some college or AA deg
_subpop_20: separated college grad or above
_subpop_21: never married less than 9th grad
_subpop_22: never married no hs diploma
_subpop_23: never married hs grad or GED
_subpop_24: never married some college or AA
_subpop_25: never married college grad or ab
_subpop_26: living with partner less than 9t
_subpop_27: living with partner no hs diplom
_subpop_28: living with partner hs grad or G
_subpop_29: living with partner some college
_subpop_30: living with partner college grad
--------------------------------------------------------------
| Linearized
Over | Mean Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
pad630 |
_subpop_1 | 123.1873 33.99413 51.46593 194.9086
_subpop_2 | 143.3616 14.00536 113.8129 172.9103
_subpop_3 | 111.808 12.92772 84.53291 139.0831
_subpop_4 | 146.2888 22.89246 97.98991 194.5877
_subpop_5 | 88.91933 8.30694 71.39322 106.4454
_subpop_6 | 176.0959 72.50964 23.11395 329.0779
_subpop_7 | 90.60535 17.21293 54.28923 126.9215
_subpop_8 | 110.4805 37.21189 31.97029 188.9907
_subpop_9 | 101.8385 11.74256 77.06389 126.6132
_subpop_10 | 260.9962 63.18704 127.6832 394.3092
_subpop_11 | 54.28887 15.49709 21.59287 86.98487
_subpop_12 | 163.2022 47.28731 63.43472 262.9697
_subpop_13 | 145.5074 25.43471 91.84482 199.1699
_subpop_14 | 129.5883 28.49053 69.47856 189.6981
_subpop_15 | 76.00663 11.32266 52.1179 99.89535
_subpop_16 | 169.3599 80.57609 -.6408196 339.3606
_subpop_17 | 165.8482 46.57393 67.58582 264.1106
_subpop_18 | 302.0225 117.2982 54.54487 549.5001
_subpop_19 | 142.5322 26.01105 87.65368 197.4107
_subpop_20 | 117.9216 34.79595 44.50859 191.3347
_subpop_21 | 309.9912 93.1523 113.4571 506.5254
_subpop_22 | 166.3335 46.45898 68.31357 264.3533
_subpop_23 | 190.2853 55.64751 72.87928 307.6913
_subpop_24 | 109.5492 15.62974 76.57336 142.5251
_subpop_25 | 126.5192 19.29269 85.81517 167.2232
_subpop_26 | 120 . . .
_subpop_27 | 144.995 24.39718 93.5215 196.4686
_subpop_28 | 98.81543 21.16077 54.17012 143.4607
_subpop_29 | 152.5923 23.7468 102.4909 202.6936
_subpop_30 | 89.0113 23.17592 40.11439 137.9082
--------------------------------------------------------------
For subpopulation 26, no standard error or confidence intervals are given. This may be cause there are very few observations at that level. To see if this is the cause, we can use the estat size command. The unweighted number of cases is given in the column titles "Obs", and the weighted (or estimated subpopulation size) is given in the column titled "Size".
estat size Over: dmdmartl dmdeduc2 _subpop_1: married less than 9th grade _subpop_2: married no hs diploma _subpop_3: married hs grad or ged _subpop_4: married some college or AA degre _subpop_5: married college grad or above _subpop_6: widowed less than 9th grade _subpop_7: widowed no hs diploma _subpop_8: widowed hs grad or ged _subpop_9: widowed some college or AA degre _subpop_10: widowed college grad or above _subpop_11: divorced less than 9th grade _subpop_12: divorced no hs diplom _subpop_13: divorced hs grad or ged _subpop_14: divorced some college or AA degr _subpop_15: divorced college grad or above _subpop_16: separated less than 9th grade _subpop_17: separated no hs diploma _subpop_18: separated hs grad or ged _subpop_19: separated some college or AA deg _subpop_20: separated college grad or above _subpop_21: never married less than 9th grad _subpop_22: never married no hs diplom _subpop_23: never married hs grad or ged _subpop_24: never married some college or AA _subpop_25: never married college grad or ab _subpop_26: living with partner less than 9t _subpop_27: living with partner no hs diplom _subpop_28: living with partner hs grad or g _subpop_29: living with partner some college _subpop_30: living with partner college grad ---------------------------------------------------------------------- | Linearized Over | Mean Std. Err. Obs Size -------------+-------------------------------------------------------- pad630 | _subpop_1 | 123.1873 33.99413 14 282303.798783 _subpop_2 | 143.3616 14.00536 36 1493852.2679 _subpop_3 | 111.808 12.92772 60 2807704.21163 _subpop_4 | 146.2888 22.89246 121 7032757.93552 _subpop_5 | 88.91933 8.30694 116 7192028.73485 _subpop_6 | 176.0959 72.50964 5 111127.083356 _subpop_7 | 90.60535 17.21293 17 562709.323876 _subpop_8 | 110.4805 37.21189 15 596030.21488 _subpop_9 | 101.8385 11.74256 27 1272472.7973 _subpop_10 | 260.9962 63.18704 9 296513.579822 _subpop_11 | 54.28887 15.49709 3 78128.930803 _subpop_12 | 163.2022 47.28731 10 414794.852531 _subpop_13 | 145.5074 25.43471 23 1215808.11627 _subpop_14 | 129.5883 28.49053 39 1738510.76294 _subpop_15 | 76.00663 11.32266 14 914950.601057 _subpop_16 | 169.3599 80.57609 4 88739.706649 _subpop_17 | 165.8482 46.57393 10 262282.787221 _subpop_18 | 302.0225 117.2982 10 327045.836107 _subpop_19 | 142.5322 26.01105 10 247858.703249 _subpop_20 | 117.9216 34.79595 4 79284.608695 _subpop_21 | 309.9912 93.1523 4 104748.202272 _subpop_22 | 166.3335 46.45898 10 343955.585817 _subpop_23 | 190.2853 55.64751 19 748235.70547 _subpop_24 | 109.5492 15.62974 79 2939581.96271 _subpop_25 | 126.5192 19.29269 37 1786563.47803 _subpop_26 | 120 0 2 83816.117097 _subpop_27 | 144.995 24.39718 9 312110.74153 _subpop_28 | 98.81543 21.16077 17 872758.146424 _subpop_29 | 152.5923 23.7468 26 1355189.31349 _subpop_30 | 89.0113 23.17592 13 796368.717456 ----------------------------------------------------------------------list pad630 if female == 1 & dmdmartl == 6 & dmdeduc2 == 1 +--------+ | pad630 | |--------| 344. | 120 | 479. | . | 1339. | . | 1962. | . | 1987. | 120 | |--------| 2075. | . | 2148. | . | 2178. | . | 2631. | . | 2972. | . | |--------| 3148. | . | 4118. | . | 4595. | . | 6610. | . | 7064. | . | |--------| 7112. | . | 7214. | . | 7709. | . | 7829. | . | 8095. | . | |--------| 8479. | . | +--------+
By using the list command, we can see that there are only two cases that have a valid value for pad630 in subpopulation 26, and both of those values are 120. This is why no standard error can be estimated.
The lincom command can be used to make comparisons between subpopulations. In the first example below, we will compare the means for males and females for hsq496 (number of days feeling anxious). We can use the display command to see how the point estimate in the output of the lincom command is calculated. The value of using the lincom command is that the standard error of point estimate is also calculated, as well as the test statistic, p-value and 95% confidence interval. In the following examples, we will compare the mean number of days feeling anxious between those who are married to those who are living with a partner, and those who are married to those who are widowed. Please see page 109 of the Stata 13 svy manual (first example in the section on survey postestimation) for more information on using lincom after the svy, subpop(): mean command.
svy, over(female): mean hsq496 (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 5883 Number of PSUs = 31 Population size = 225667462 Design df = 17 male: female = male female: female = female -------------------------------------------------------------- | Linearized Over | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ hsq496 | male | 4.589723 .1956524 4.176933 5.002514 female | 6.153479 .2675166 5.589069 6.71789 -------------------------------------------------------------- lincom [hsq496]male - [hsq496]female ( 1) [hsq496]male - [hsq496]female = 0 ------------------------------------------------------------------------------ Mean | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | -1.563756 .2702582 -5.79 0.000 -2.133951 -.9935614 ------------------------------------------------------------------------------display 4.589723 - 6.153479 -1.563756 svy, over(dmdmartl): mean hsq496 (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 4692 Number of PSUs = 31 Population size = 193938169 Design df = 17 married: dmdmartl = married widowed: dmdmartl = widowed divorced: dmdmartl = divorced separated: dmdmartl = separated _subpop_5: dmdmartl = never married _subpop_6: dmdmartl = living with partner -------------------------------------------------------------- | Linearized Over | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ hsq496 | married | 4.915051 .2864456 4.310704 5.519399 widowed | 5.450213 .3868792 4.633969 6.266457 divorced | 7.514127 .473958 6.514163 8.514091 separated | 7.231938 1.136924 4.833238 9.630637 _subpop_5 | 6.223865 .408766 5.361444 7.086286 _subpop_6 | 7.266146 .6322425 5.93223 8.600061 -------------------------------------------------------------- lincom [hsq496]married - [hsq496]_subpop_6 ( 1) [hsq496]married - [hsq496]_subpop_6 = 0 ------------------------------------------------------------------------------ Mean | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | -2.351094 .6468052 -3.63 0.002 -3.715734 -.9864544 ------------------------------------------------------------------------------ lincom [hsq496]married - [hsq496]widowed ( 1) [hsq496]married - [hsq496]widowed = 0 ------------------------------------------------------------------------------ Mean | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- (1) | -.5351614 .5175658 -1.03 0.316 -1.62713 .5568069 ------------------------------------------------------------------------------Graphing with continuous variables
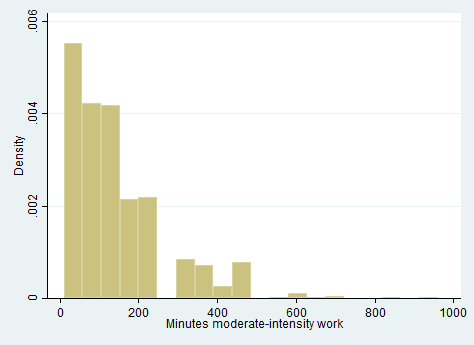
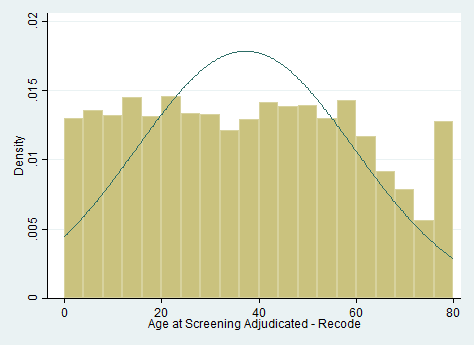
We can also get some descriptive graphs of our variables. For a continuous variable, you may want a histogram. However, the histogram command will only accept a frequency weight, which, by definition, can have only integer values. A suggestion by Heeringa, West and Berglund (2010, pages 121-122) is to simply use the integer part of the sampling weight. We can create a frequency weight from our sampling weight using the generate command with the int function.
gen int_wtint2yr = int(wtint2yr) histogram pad630 [fw = int_wtint2yr], bin(20)histogram ridageyr [fw = int_wtint2yr], bin(20) normal
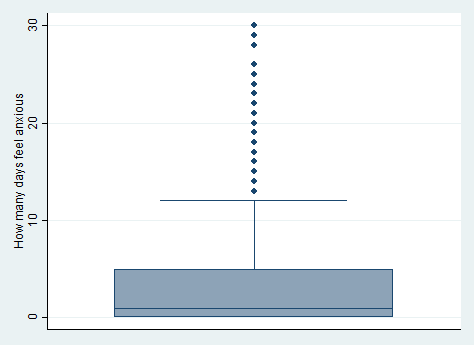
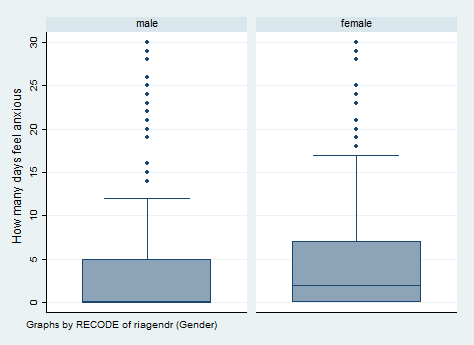
We can make box plots and use the sampling weight that is provided in the data set.
graph box hsq496 [pw = wtint2yr]graph box hsq496 [pw = wtint2yr], by(female) ylabel(0(5)30)* the line is the box plot represents the median, not the mean svy, over(female): mean hsq496 (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 5883 Number of PSUs = 31 Population size = 225667462 Design df = 17 male: female = male female: female = female -------------------------------------------------------------- | Linearized Over | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ hsq496 | male | 4.589723 .1956524 4.176933 5.002514 female | 6.153479 .2675166 5.589069 6.71789 -------------------------------------------------------------- estat sd male: female = male female: female = female ------------------------------------- Over | Mean Std. Dev. -------------+----------------------- hsq496 | male | 4.589723 8.408553 female | 6.153479 9.096215 -------------------------------------
We can use the svy: total command to get totals. The values in the output can get to be very large, so we can use the estimates table command to see them. We can also use the matrix list command.
svy: total pad630 (running total on estimation sample) Survey: Total estimation Number of strata = 14 Number of obs = 2054 Number of PSUs = 31 Population size = 88768571 Design df = 17 -------------------------------------------------------------- | Linearized | Total Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ pad630 | 1.24e+10 1.07e+09 1.02e+10 1.47e+10 -------------------------------------------------------------- estimates table, b(%15.2f) se(%13.2f) -------------------------------- Variable | active -------------+------------------ pad630 | 12417602483.56 | 1065724292.32 -------------------------------- legend: b/se svy: total pad630 (running total on estimation sample) Survey: Total estimation Number of strata = 14 Number of obs = 2054 Number of PSUs = 31 Population size = 88768571 Design df = 17 -------------------------------------------------------------- | Linearized | Total Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ pad630 | 1.24e+10 1.07e+09 1.02e+10 1.47e+10 -------------------------------------------------------------- matlist e(b), format(%15.2f) | pad630 -------------+----------------- y1 | 12417602483.56 svy, over(female): total pad630 (running total on estimation sample) Survey: Total estimation Number of strata = 14 Number of obs = 2054 Number of PSUs = 31 Population size = 88768571 Design df = 17 male: female = male female: female = female -------------------------------------------------------------- | Linearized Over | Total Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ pad630 | male | 7.41e+09 6.37e+08 6.06e+09 8.75e+09 female | 5.01e+09 4.72e+08 4.01e+09 6.00e+09 -------------------------------------------------------------- estimates table, b(%15.2f) se(%13.2f) -------------------------------- Variable | active -------------+------------------ male | 7408679626.25 | 637463721.35 female | 5008922857.30 | 472105366.03 -------------------------------- legend: b/seRelationships between two continuous variables
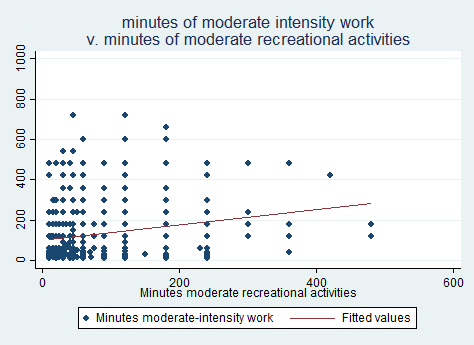
Let’s look at some bivariate relationships. As of Stata 13.1, we cannot get correlations with survey data (but you can with SUDAAN 11). The graphical version of a correlation is a scatterplot, which we show below. We will include the fit line.
svy: mean pad630 pad675 (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 1030 Number of PSUs = 31 Population size = 48053490 Design df = 17 -------------------------------------------------------------- | Linearized | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ pad630 | 129.7198 5.723011 117.6453 141.7943 pad675 | 72.48499 2.365431 67.49436 77.47561 -------------------------------------------------------------- twoway (scatter pad630 pad675) (lfit pad630 pad675 [pw = wtint2yr]), /// title("minutes of moderate intensity work" /// "v. minutes of moderate recreational activities")Descriptive statistics with categorical variables
Let’s get some descriptive statistics with categorical variables. We can use the svy: tab and svy: proportion commands. We will use the marital status variable, dmdmart1, which has six levels. When used with no options, the output from the svy: tab command will give us the same information as the svy: proportion command.
svy: tab dmdmartl
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
-----------------------
Marital |
Status | proportions
----------+------------
married | .5308
widowed | .0562
divorced | .1069
separate | .024
never ma | .1987
living w | .0834
|
Total | 1
-----------------------
Key: proportions = cell proportions
svy: proportion dmdmartl
(running proportion on estimation sample)
Survey: Proportion estimation
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
_prop_5: dmdmartl = never married
_prop_6: dmdmartl = living with partner
--------------------------------------------------------------
| Linearized
| Proportion Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
dmdmartl |
married | .5307919 .0204953 .4874276 .5736962
widowed | .0562251 .0031996 .0498433 .0633695
divorced | .1068817 .007248 .0925245 .1231643
separated | .0239747 .0031613 .0181365 .0316316
_prop_5 | .1986955 .0236294 .1534768 .2532512
_prop_6 | .0834312 .0064732 .070751 .0981439
--------------------------------------------------------------
Let’s use some options with the svy: tab command so that we can see the estimated number of people in each category.
svy: tab dmdmartl, count cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
------------------------
Marital |
Status | count
----------+-------------
married | 118822198
widowed | 12586462
divorced | 23926362
separate | 5366932
never ma | 44479637
living w | 18676762
|
Total | 223858353
------------------------
Key: count = weighted counts
There are many options that can by used with svy: tab. Please see the Stata help file for the svy: tabulate command for a complete listing and description of each option. Only five items can be displayed at once, and the ci option counts as two items.
svy: tab dmdmartl, cell count obs cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
----------------------------------------------------
Marital |
Status | count proportions obs
----------+-----------------------------------------
married | 118822198 .53 2683
widowed | 12586462 .056 467
divorced | 23926362 .11 571
separate | 5366932 .024 204
never ma | 44479637 .2 1188
living w | 18676762 .083 440
|
Total | 223858353 1 5553
----------------------------------------------------
Key: count = weighted counts
proportions = cell proportions
obs = number of observations
svy: tab dmdmartl, count se cellwidth(15) format(%15.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
--------------------------------------------
Marital |
Status | count se
----------+---------------------------------
married | 118822198 10556102
widowed | 12586462 1087437
divorced | 23926362 2606988
separate | 5366932 614868
never ma | 44479637 4687152
living w | 18676762 1874572
|
Total | 223858353
--------------------------------------------
Key: count = weighted counts
se = linearized standard errors of weighted counts
svy: tab dmdmartl, count deff deft cv cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
------------------------------------------------------------------
Marital |
Status | count cv deff deft
----------+-------------------------------------------------------
married | 118822198 8.9 50 7
widowed | 12586462 8.6 2.5 1.6
divorced | 23926362 11 7.9 2.8
separate | 5366932 11 1.8 1.3
never ma | 44479637 11 15 3.9
living w | 18676762 10 5.1 2.3
|
Total | 223858353
------------------------------------------------------------------
Key: count = weighted counts
cv = coefficients of variation of weighted counts
deff = deff for variances of weighted counts
deft = deft for variances of weighted counts
Chi-square tests are provided by default when svy: tab is issued with two variables. You will usually want to use the design-based test.
The proportion of observations in each cell can be obtained using either the svy: tab or the svy: proportion command. If you want to compare the proportions within two cells, you can use the lincom command.
svy: tab dmdmartl female, cell obs count cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
----------------------------------------------------
Marital | RECODE of riagendr (Gender)
Status | male female Total
----------+-----------------------------------------
married | 58666065 60156133 118822198
| .26 .27 .53
| 1429 1254 2683
|
widowed | 2732447 9854015 12586462
| .012 .044 .056
| 122 345 467
|
divorced | 9287612 14638749 23926362
| .041 .065 .11
| 237 334 571
|
separate | 2019361 3347571 5366932
| .009 .015 .024
| 79 125 204
|
never ma | 25152255 19327382 44479637
| .11 .086 .2
| 634 554 1188
|
living w | 9529522 9147240 18676762
| .043 .041 .083
| 237 203 440
|
Total | 107387263 116471090 223858353
| .48 .52 1
| 2738 2815 5553
----------------------------------------------------
Key: weighted counts
cell proportions
number of observations
Pearson:
Uncorrected chi2(5) = 148.4759
Design-based F(3.19, 54.18) = 22.0446 P = 0.0000
svy: proportion dmdmartl, over(female)
(running proportion on estimation sample)
Survey: Proportion estimation
Number of strata = 14 Number of obs = 5553
Number of PSUs = 31 Population size = 223858353
Design df = 17
married: dmdmartl = married
widowed: dmdmartl = widowed
divorced: dmdmartl = divorced
separated: dmdmartl = separated
_prop_5: dmdmartl = never married
_prop_6: dmdmartl = living with partner
male: female = male
female: female = female
--------------------------------------------------------------
| Linearized
Over | Proportion Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
married |
male | .5463038 .0244819 .494338 .5972798
female | .5164898 .0186122 .4772006 .5555763
-------------+------------------------------------------------
widowed |
male | .0254448 .0029445 .0199183 .0324539
female | .0846048 .005444 .0738042 .0968207
-------------+------------------------------------------------
divorced |
male | .0864871 .0103046 .0670772 .1108462
female | .1256857 .0097098 .1065877 .1476401
-------------+------------------------------------------------
separated |
male | .0188045 .0035212 .0126507 .0278672
female | .0287416 .0042363 .0210327 .0391631
-------------+------------------------------------------------
_prop_5 |
male | .2342201 .0271275 .1818695 .2961843
female | .1659415 .021306 .1257079 .2158725
-------------+------------------------------------------------
_prop_6 |
male | .0887398 .0077162 .0737516 .106424
female | .0785366 .0066277 .0656434 .0937081
--------------------------------------------------------------
lincom [married]male - [married]female
( 1) [married]male - [married]female = 0
------------------------------------------------------------------------------
Proportion | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .0298139 .0132293 2.25 0.038 .0019026 .0577253
------------------------------------------------------------------------------
display .5463038 - .5164898
.029814
Graphs with categorical variables
Let’s create a bar graph of the variable female. This graph will show the percent of observations that are female and male. To do this, we will need to create a new variable, which we will call male; it will be the opposite of female.
gen male = !female graph bar (mean) female male [pw = wtint2yr], percentages bargap(7)
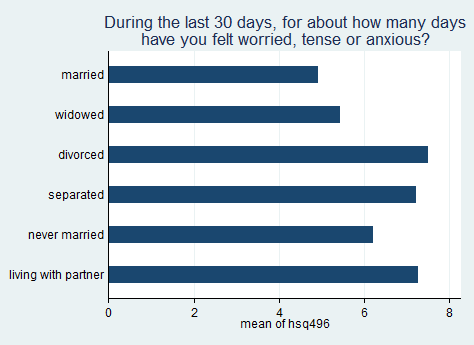
We can also graph the mean of the variable hsq496 by each level of dmdmart1.
svy: mean hsq496, over(dmdmartl) (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 4692 Number of PSUs = 31 Population size = 193938169 Design df = 17 married: dmdmartl = married widowed: dmdmartl = widowed divorced: dmdmartl = divorced separated: dmdmartl = separated _subpop_5: dmdmartl = never married _subpop_6: dmdmartl = living with partner -------------------------------------------------------------- | Linearized Over | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ hsq496 | married | 4.915051 .2864456 4.310704 5.519399 widowed | 5.450213 .3868792 4.633969 6.266457 divorced | 7.514127 .473958 6.514163 8.514091 separated | 7.231938 1.136924 4.833238 9.630637 _subpop_5 | 6.223865 .408766 5.361444 7.086286 _subpop_6 | 7.266146 .6322425 5.93223 8.600061 -------------------------------------------------------------- graph hbar hsq496 [pw = wtint2yr], over(dmdmartl, gap(*2)) /// title("During the last 30 days, for about how many days" /// "have you felt worried, tense or anxious?")
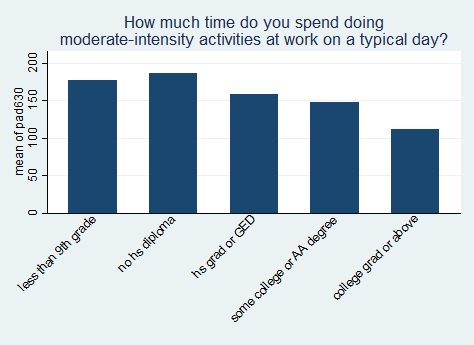
Finally, we will graph the mean of pad630 for each level of dmdeduc2.
svy: mean pad630, over(dmdeduc2) (running mean on estimation sample) Survey: Mean estimation Number of strata = 14 Number of obs = 1706 Number of PSUs = 31 Population size = 77856183 Design df = 17 _subpop_1: dmdeduc2 = less than 9th grade _subpop_2: dmdeduc2 = no hs diploma _subpop_3: dmdeduc2 = hs grad or GED _subpop_4: dmdeduc2 = some college or AA degree _subpop_5: dmdeduc2 = college grad or above -------------------------------------------------------------- | Linearized Over | Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------ pad630 | _subpop_1 | 176.8361 19.65517 135.3673 218.3048 _subpop_2 | 186.4248 6.52083 172.6671 200.1826 _subpop_3 | 157.9824 7.430086 142.3063 173.6585 _subpop_4 | 147.1004 10.20694 125.5657 168.6352 _subpop_5 | 111.1123 7.475883 95.3396 126.8851 --------------------------------------------------------------graph bar pad630 [pw = wtint2yr], over(dmdeduc2, label(angle(45))) /// title("How much time do you spend doing" /// "moderate-intensity activities at work on a typical day?")OLS regression
Now that we have descriptive statistics on our variables, we may want to run some inferential statistics, such as OLS regression or logistic regression. As before, we simply need to use the svy: prefix before our regression commands.
Please note that the following analyses are shown only as examples of how to do these analyses in Stata. There was no attempt to create substantively meaningful models. Rather, the variables were chosen for illustrative purposes only. We do not recommend that researchers create their models this way.
We will start with an OLS regression with one categorical predictor (female) and one continuous predictor (ridageyr). We will follow the svy: regress command with the margins command, which gives us the predicted values for each level of female.
Notice that we use the vce(unconditional) option with each call to margins. The following information is quoted from the Stata 13 svy manual, page 113: When performing estimations with linearized standard errors, we use the vce(unconditional) option to compute marginal effects so that we can use the results to make inferences on the population. margins with vce(unconditional) uses linearization to compute the unconditional variance of the marginal means.
svy: regress pad630 i.female ridageyr
(running regress on estimation sample)
Survey: Linear regression
Number of strata = 14 Number of obs = 2054
Number of PSUs = 31 Population size = 88768571
Design df = 17
F( 2, 16) = 17.18
Prob > F = 0.0001
R-squared = 0.0193
------------------------------------------------------------------------------
| Linearized
pad630 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female |
female | -33.12513 6.018746 -5.50 0.000 -45.82358 -20.42669
ridageyr | -.287604 .1289996 -2.23 0.040 -.5597695 -.0154386
_cons | 167.2895 9.314455 17.96 0.000 147.6378 186.9413
------------------------------------------------------------------------------
margins female, vce(unconditional)
Predictive margins Number of obs = 2054
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Linearized
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female |
male | 155.248 6.994755 22.19 0.000 140.4903 170.0056
female | 122.1228 5.366491 22.76 0.000 110.8005 133.4452
------------------------------------------------------------------------------
Now let’s run a model with a categorical by categorical interaction term. We can use the contrast command to get the test of the interaction displayed as an F-test rather than a t-statistic. Of course, the p-value is exactly the same. We can use the margins command to get the predicted values of pad630 for each combination of female and hsq571. The marginsplot command is used to obtain a graph of the interaction (marginsplot graphs the values shown in the output from the margins command).
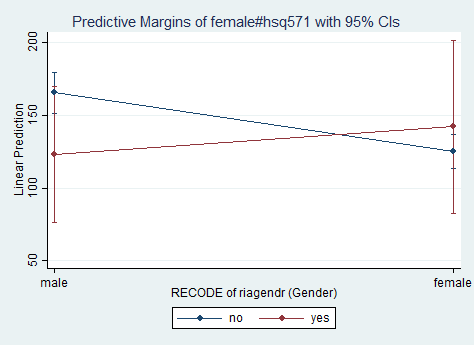
svy: regress pad630 i.female##i.hsq571 ridageyr (running regress on estimation sample) Survey: Linear regression Number of strata = 14 Number of obs = 1673 Number of PSUs = 31 Population size = 76183526 Design df = 17 F( 4, 14) = 22.40 Prob > F = 0.0000 R-squared = 0.0457 ------------------------------------------------------------------------------- | Linearized pad630 | Coef. Std. Err. t P>|t| [95% Conf. Interval] --------------+---------------------------------------------------------------- female | female | -40.42599 6.586285 -6.14 0.000 -54.32184 -26.53014 | hsq571 | yes | -42.38641 19.18468 -2.21 0.041 -82.86254 -1.910279 | female#hsq571 | female#yes | 59.28491 19.63991 3.02 0.008 17.84833 100.7215 | ridageyr | -.9869588 .2047143 -4.82 0.000 -1.418868 -.5550493 _cons | 209.1557 11.97401 17.47 0.000 183.8927 234.4186 ------------------------------------------------------------------------------- contrast female#hsq571 Contrasts of marginal linear predictions Design df = 17 Margins : asbalanced ------------------------------------------------- | df F P>F --------------+---------------------------------- female#hsq571 | 1 9.11 0.0077 Design | 17 ------------------------------------------------- Note: F statistics are adjusted for the survey design. margins female#hsq571, vce(unconditional) Predictive margins Number of obs = 1673 Expression : Linear prediction, predict() ------------------------------------------------------------------------------- | Linearized | Margin Std. Err. t P>|t| [95% Conf. Interval] --------------+---------------------------------------------------------------- female#hsq571 | male#no | 165.6268 6.65576 24.88 0.000 151.5844 179.6692 male#yes | 123.2404 22.22847 5.54 0.000 76.34241 170.1383 female#no | 125.2008 5.586263 22.41 0.000 113.4148 136.9868 female#yes | 142.0993 28.20328 5.04 0.000 82.59557 201.603 -------------------------------------------------------------------------------marginsplot Variables that uniquely identify margins: female hsq571
In this example, we will use a categorical by continuous interaction. In the first call to the margins command, we get the simple slope coefficients for males and females. The p-values in this table tell us that both slopes are significantly different from 0. In the second call to the margins command, we get the predicted values for each level of female at pad680 = 0, pad680 = 200, pad680 = 400, up to pad680 = 1400. The t-statistics and corresponding p-values tell us if the predicted value is different from 0.
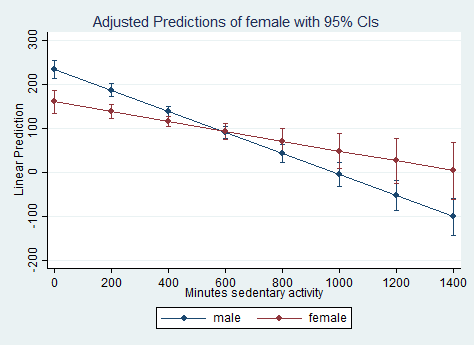
svy: regress pad630 i.female##c.pad680 (running regress on estimation sample) Survey: Linear regression Number of strata = 14 Number of obs = 2050 Number of PSUs = 31 Population size = 88700876 Design df = 17 F( 3, 15) = 131.11 Prob > F = 0.0000 R-squared = 0.0894 --------------------------------------------------------------------------------- | Linearized pad630 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ----------------+---------------------------------------------------------------- female | female | -73.89628 18.78819 -3.93 0.001 -113.5359 -34.25665 pad680 | -.2389814 .0194172 -12.31 0.000 -.2799481 -.1980148 | female#c.pad680 | female | .1273678 .0445652 2.86 0.011 .0333435 .2213922 | _cons | 234.2159 9.710639 24.12 0.000 213.7282 254.7035 --------------------------------------------------------------------------------- margins female, dydx(pad680) vce(unconditional) Average marginal effects Number of obs = 2050 Expression : Linear prediction, predict() dy/dx w.r.t. : pad680 ------------------------------------------------------------------------------ | Linearized | dy/dx Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- pad680 | female | male | -.2389814 .0194172 -12.31 0.000 -.2799481 -.1980148 female | -.1116136 .0293859 -3.80 0.001 -.1736123 -.0496149 ------------------------------------------------------------------------------ margins female, at(pad680=(0(200)1400)) vsquish vce(unconditional) Adjusted predictions Number of obs = 2050 Expression : Linear prediction, predict() 1._at : pad680 = 0 2._at : pad680 = 200 3._at : pad680 = 400 4._at : pad680 = 600 5._at : pad680 = 800 6._at : pad680 = 1000 7._at : pad680 = 1200 8._at : pad680 = 1400 ------------------------------------------------------------------------------ | Linearized | Margin Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _at#female | 1#male | 234.2159 9.710639 24.12 0.000 213.7282 254.7035 1#female | 160.3196 12.25815 13.08 0.000 134.4572 186.182 2#male | 186.4196 6.921151 26.93 0.000 171.8173 201.022 2#female | 137.9969 7.310548 18.88 0.000 122.573 153.4208 3#male | 138.6233 5.627637 24.63 0.000 126.75 150.4966 3#female | 115.6742 5.070343 22.81 0.000 104.9767 126.3717 4#male | 90.82704 6.752807 13.45 0.000 76.57986 105.0742 4#female | 93.35145 8.188708 11.40 0.000 76.07479 110.6281 5#male | 43.03076 9.470621 4.54 0.000 23.04949 63.01202 5#female | 71.02874 13.3223 5.33 0.000 42.92113 99.13634 6#male | -4.765528 12.80418 -0.37 0.714 -31.77999 22.24893 6#female | 48.70602 18.89431 2.58 0.020 8.842508 88.56953 7#male | -52.56181 16.38181 -3.21 0.005 -87.1244 -17.99922 7#female | 26.3833 24.60871 1.07 0.299 -25.53653 78.30313 8#male | -100.3581 20.07342 -5.00 0.000 -142.7093 -58.00688 8#female | 4.060579 30.38526 0.13 0.895 -60.04672 68.16788 ------------------------------------------------------------------------------marginsplot Variables that uniquely identify margins: pad680 femaleIn the example below, we get the difference between the predicted values for males and females at eight values of pad680. We then use the marginsplot command to graph these differences. This graph shows that the difference between males and females is larger at the extreme values of pad680, as is the variability around those estimates.
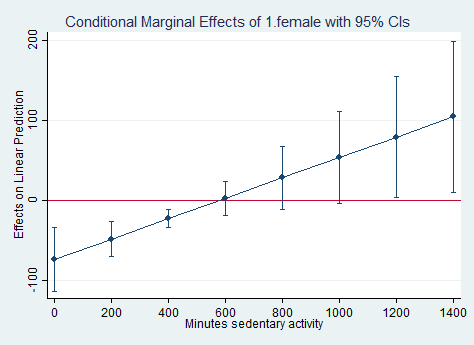
Notice that is in the output from the margins command above, the predicted value for 4#female is 93.35145 and the predicted value for 4#male is 90.82704. 93.35145-90.82704 = 2.52441, which is the value of dy/dx on line 4 of the output below. The corresponding p-value is .808, which is not statistically significant. You can see this in the graph above, where the point for males and females appear to be on top of each other.
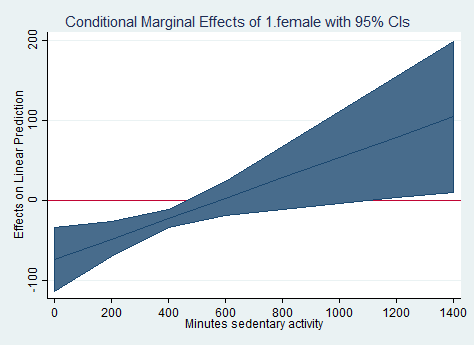
margins, dydx(female) at(pad680=(0(200)1400)) vsquish vce(unconditional) Conditional marginal effects Number of obs = 2050 Expression : Linear prediction, predict() dy/dx w.r.t. : 1.female 1._at : pad680 = 0 2._at : pad680 = 200 3._at : pad680 = 400 4._at : pad680 = 600 5._at : pad680 = 800 6._at : pad680 = 1000 7._at : pad680 = 1200 8._at : pad680 = 1400 ------------------------------------------------------------------------------ | Linearized | dy/dx Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- 1.female | _at | 1 | -73.89628 18.78819 -3.93 0.001 -113.5359 -34.25665 2 | -48.42271 10.55029 -4.59 0.000 -70.68189 -26.16354 3 | -22.94915 5.339066 -4.30 0.000 -34.21359 -11.6847 4 | 2.524416 10.22678 0.25 0.808 -19.05221 24.10104 5 | 27.99798 18.42697 1.52 0.147 -10.87952 66.87548 6 | 53.47154 27.08143 1.97 0.065 -3.665269 110.6084 7 | 78.94511 35.86278 2.20 0.042 3.281267 154.609 8 | 104.4187 44.69629 2.34 0.032 10.11775 198.7196 ------------------------------------------------------------------------------ Note: dy/dx for factor levels is the discrete change from the base level.marginsplot, yline(0) Variables that uniquely identify margins: pad680marginsplot, recast(line) recastci(rarea) yline(0) Variables that uniquely identify margins: pad680
If we use a categorical predictor variable in our model that has more than two levels, we may want to run comparisons between each of the levels. In the example below, we use the educational attainment variable, dmdeduc2, as a predictor. We use the contrast command to determine if, taken together, dmdeduc2, is a statistically significant predictor of our outcome variable, pad630. Next, we use the pwcompare command to conduct all pairwise comparisons. We use the mcompare(sidak) option to adjust the p-values for the multiple comparisons, and we use the pveffects option to have the test statistics and p-values shown in the output. Other options that we could have used with the mcompare option are bonferroni and scheffe.
svy: regress pad630 i.dmdeduc2 ridageyr
(running regress on estimation sample)
Survey: Linear regression
Number of strata = 14 Number of obs = 1706
Number of PSUs = 31 Population size = 77856183
Design df = 17
F( 5, 13) = 14.67
Prob > F = 0.0001
R-squared = 0.0541
--------------------------------------------------------------------------------------------
| Linearized
pad630 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------------------------+----------------------------------------------------------------
dmdeduc2 |
no hs diploma | 5.590284 17.44227 0.32 0.752 -31.20968 42.39025
hs grad or GED | -23.40642 18.92372 -1.24 0.233 -63.33198 16.51915
some college or AA degree | -36.62121 23.10453 -1.59 0.131 -85.36752 12.12509
college grad or above | -69.28669 22.12513 -3.13 0.006 -115.9666 -22.60674
|
ridageyr | -1.167769 .2339256 -4.99 0.000 -1.661309 -.6742287
_cons | 235.0531 18.73331 12.55 0.000 195.5293 274.5769
--------------------------------------------------------------------------------------------
contrast dmdeduc2
Contrasts of marginal linear predictions
Design df = 17
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
dmdeduc2 | 4 14.46 0.0001
Design | 17
------------------------------------------------
Note: F statistics are adjusted for the survey
design.
pwcompare dmdeduc2, mcompare(sidak) cformat(%3.1f) pveffects
Pairwise comparisons of marginal linear predictions
Design df = 17
Margins : asbalanced
---------------------------
| Number of
| Comparisons
-------------+-------------
dmdeduc2 | 10
---------------------------
--------------------------------------------------------------------------------------------
| Sidak
| Contrast Std. Err. t P>|t|
----------------------------------------------------+---------------------------------------
dmdeduc2 |
no hs diploma vs less than 9th grade | 5.6 17.4 0.32 1.000
hs grad or GED vs less than 9th grade | -23.4 18.9 -1.24 0.929
some college or AA degree vs less than 9th grade | -36.6 23.1 -1.59 0.756
college grad or above vs less than 9th grade | -69.3 22.1 -3.13 0.059
hs grad or GED vs no hs diploma | -29.0 9.8 -2.95 0.087
some college or AA degree vs no hs diploma | -42.2 10.0 -4.23 0.006
college grad or above vs no hs diploma | -74.9 10.2 -7.31 0.000
some college or AA degree vs hs grad or GED | -13.2 13.9 -0.95 0.988
college grad or above vs hs grad or GED | -45.9 13.2 -3.47 0.029
college grad or above vs some college or AA degree | -32.7 12.2 -2.68 0.147
--------------------------------------------------------------------------------------------
Logistic regression
Let’s run a logistic regression. We will use the variable paq665 (do you do any moderate-intensity sports, fitness or recreational activities that cause a small increase in breathing or heart rate at least 10 minutes continually?) as the outcome variable. We will also limit the analysis to those who are greater than age 20. Before we run our logistic regression, let’s look at the distribution of the outcome variable, and let’s look at the crosstabulation of the outcome variable with our categorical predictor variable. The purpose of the first descriptive analysis is to assess the proportion and number of cases in each level of the outcome variable. If we found that there was a very small proportion of cases in one of the levels, we may encounter estimation problems with the logistic regression. Likewise, if the crosstabulation between the outcome variable and the categorical predictor variable showed that one or more cells had very few unweighted observations or no observations at all, we might want to recode the predictor variable into fewer categories so that there were a sufficient number of observations in each cell. The results below do not look problematic, although there are relatively few observations that are coded as 1 on our outcome variable and 5 on our predictor variable. This might increase the standard error around that point estimate.
svy, subpop(if ridageyr > 20): tab paq665, ///
cell obs count cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 9755
Number of PSUs = 31 Population size = 306516207
Subpop. no. of obs = 5443
Subpop. size = 218554854
Design df = 17
----------------------------------------------------
Moderate |
recreatio |
nal |
activitie |
s | count proportions obs
----------+-----------------------------------------
no | 116709772 .53 3195
yes | 101845081 .47 2248
|
Total | 218554854 1 5443
----------------------------------------------------
Key: count = weighted counts
proportions = cell proportions
obs = number of observations
svy, subpop(if ridageyr > 20): tab hsd010 paq665, ///
cell obs count cellwidth(12) format(%12.2g)
(running tabulate on estimation sample)
Number of strata = 14 Number of obs = 8915
Number of PSUs = 31 Population size = 277379812
Subpop. no. of obs = 4603
Subpop. size = 189418459
Design df = 17
----------------------------------------------------
General |
health | Moderate recreational activities
condition | no yes Total
----------+-----------------------------------------
excellen | 9401577 13365343 22766920
| .05 .071 .12
| 223 234 457
|
very goo | 27412706 34747263 62159969
| .14 .18 .33
| 591 650 1241
|
good | 41493331 31885029 73378359
| .22 .17 .39
| 1092 753 1845
|
fair | 18274770 8295293 26570064
| .096 .044 .14
| 634 256 890
|
poor | 3896015 647132 4543147
| .021 .0034 .024
| 145 25 170
|
Total | 100478399 88940060 189418459
| .53 .47 1
| 2685 1918 4603
----------------------------------------------------
Key: weighted counts
cell proportions
number of observations
Pearson:
Uncorrected chi2(4) = 386.5375
Design-based F(2.76, 46.90) = 35.0850 P = 0.0000
Now let’s run the logistic regression. We can use the contrast command to get the multi-degree-of-freedom test of hsd010.
svy, subpop(if ridageyr > 20): logit paq665 ib3.hsd010 c.ridageyr
(running logit on estimation sample)
Survey: Logistic regression
Number of strata = 14 Number of obs = 8915
Number of PSUs = 31 Population size = 277379812
Subpop. no. of obs = 4603
Subpop. size = 189418459
Design df = 17
F( 5, 13) = 37.01
Prob > F = 0.0000
------------------------------------------------------------------------------
| Linearized
paq665 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
hsd010 |
excellent | .5986804 .1120919 5.34 0.000 .3621872 .8351736
very good | .4914449 .1141339 4.31 0.000 .2506434 .7322465
fair | -.4945664 .1127125 -4.39 0.000 -.7323691 -.2567638
poor | -1.450551 .2048429 -7.08 0.000 -1.882732 -1.01837
|
ridageyr | -.0109676 .00292 -3.76 0.002 -.0171282 -.004807
_cons | .2653286 .1382701 1.92 0.072 -.0263958 .557053
------------------------------------------------------------------------------
contrast hsd010
Contrasts of marginal linear predictions
Design df = 17
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
hsd010 | 4 44.44 0.0000
Design | 17
------------------------------------------------
Note: F statistics are adjusted for the survey
design.
Let’s include a categorical by continuous interaction in the model. We will use the contrast command to determine if the interaction term (as a whole) is statistically significant. We will use the contrast command to get the multi-degree-of-freedom test of the interaction, the margins command to get the predicted probabilities and the marginsplot command to graph the interaction.
svy, subpop(if ridageyr > 20): logit paq665 ib3.hsd010##c.ridageyr (running logit on estimation sample) Survey: Logistic regression Number of strata = 14 Number of obs = 8915 Number of PSUs = 31 Population size = 277379812 Subpop. no. of obs = 4603 Subpop. size = 189418459 Design df = 17 F( 9, 9) = 50.07 Prob > F = 0.0000 ----------------------------------------------------------------------------------- | Linearized paq665 | Coef. Std. Err. t P>|t| [95% Conf. Interval] ------------------+---------------------------------------------------------------- hsd010 | excellent | .3858144 .5191089 0.74 0.467 -.7094096 1.481038 very good | .652864 .2254827 2.90 0.010 .1771372 1.128591 fair | .3499552 .3042182 1.15 0.266 -.2918891 .9917995 poor | -.9774887 1.318543 -0.74 0.469 -3.759372 1.804395 | ridageyr | -.0083106 .004617 -1.80 0.090 -.0180516 .0014303 | hsd010#c.ridageyr | excellent | .0046206 .0101254 0.46 0.654 -.0167421 .0259833 very good | -.0033669 .0042601 -0.79 0.440 -.0123549 .0056211 fair | -.0170309 .0064368 -2.65 0.017 -.0306114 -.0034504 poor | -.0090097 .0265987 -0.34 0.739 -.0651279 .0471086 | _cons | .1376637 .2029975 0.68 0.507 -.2906237 .5659511 ----------------------------------------------------------------------------------- contrast hsd010#c.ridageyr Contrasts of marginal linear predictions Design df = 17 Margins : asbalanced ----------------------------------------------------- | df F P>F ------------------+---------------------------------- hsd010#c.ridageyr | 4 4.73 0.0126 Design | 17 ----------------------------------------------------- Note: F statistics are adjusted for the survey design.margins hsd010, subpop(if ridageyr > 20) at(ridageyr=(20(10)80)) /// vsquish vce(unconditional) Adjusted predictions Number of obs = 8915 Subpop. no. of obs = 4603 Expression : Pr(paq665), predict() 1._at : ridageyr = 20 2._at : ridageyr = 30 3._at : ridageyr = 40 4._at : ridageyr = 50 5._at : ridageyr = 60 6._at : ridageyr = 70 7._at : ridageyr = 80 ------------------------------------------------------------------------------ | Linearized | Margin Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _at#hsd010 | 1#excellent | .6105625 .0627257 9.73 0.000 .4782229 .7429022 1#very good | .6357529 .030173 21.07 0.000 .5720935 .6994123 1#good | .4928633 .0299032 16.48 0.000 .4297731 .5559535 1#fair | .4951972 .0374002 13.24 0.000 .4162897 .5741046 1#poor | .2339337 .1366427 1.71 0.105 -.0543571 .5222245 2#excellent | .6017536 .0467599 12.87 0.000 .5030987 .7004084 2#very good | .6083073 .0251426 24.19 0.000 .555261 .6613536 2#good | .4721152 .0212358 22.23 0.000 .4273116 .5169188 2#fair | .4322622 .0318406 13.58 0.000 .3650845 .4994399 2#poor | .2043323 .0853799 2.39 0.029 .0241965 .3844681 3#excellent | .5928782 .0329296 18.00 0.000 .5234028 .6623537 3#very good | .5801593 .0224851 25.80 0.000 .5327198 .6275988 3#good | .451463 .0165591 27.26 0.000 .4165264 .4863996 3#fair | .3714403 .0279114 13.31 0.000 .3125525 .4303282 3#poor | .1776082 .043438 4.09 0.001 .0859621 .2692544 4#excellent | .5839418 .0257247 22.70 0.000 .5296674 .6382163 4#very good | .55148 .0236447 23.32 0.000 .501594 .6013659 4#good | .4309767 .0189088 22.79 0.000 .3910827 .4708706 4#fair | .3144367 .0261895 12.01 0.000 .2591816 .3696917 4#poor | .1537041 .0180881 8.50 0.000 .1155416 .1918666 5#excellent | .5749499 .0307861 18.68 0.000 .5099969 .6399029 5#very good | .5224542 .0284286 18.38 0.000 .4624752 .5824332 5#good | .4107239 .0261597 15.70 0.000 .3555316 .4659161 5#fair | .2625274 .0261464 10.04 0.000 .2073633 .3176914 5#poor | .1324989 .030077 4.41 0.000 .0690418 .1959559 6#excellent | .5659081 .0443458 12.76 0.000 .4723467 .6594696 6#very good | .4932759 .0354001 13.93 0.000 .4185883 .5679635 6#good | .3907692 .0350558 11.15 0.000 .3168079 .4647305 6#fair | .2164816 .0266714 8.12 0.000 .1602098 .2727533 6#poor | .1138257 .0489862 2.32 0.033 .0104739 .2171774 7#excellent | .5568223 .0611297 9.11 0.000 .4278498 .6857948 7#very good | .4641434 .0433376 10.71 0.000 .3727091 .5555776 7#good | .3711734 .0442524 8.39 0.000 .277809 .4645377 7#fair | .1765782 .026898 6.56 0.000 .1198284 .2333281 7#poor | .0974883 .0635355 1.53 0.143 -.0365598 .2315365 ------------------------------------------------------------------------------marginsplotVariables that uniquely identify margins: ridageyr hsd010
For our last example, we will run a logistic regression model and use the estat gof command to get the Archer-Lemeshow test (which is a modification of the Hosmer-Lemeshow test that can be used with survey data). The numerator degrees of freedom are calculated as g - 1, and the denominator degrees of freedom are calculated as f - g + 2, where f = the number of sampled clusters - the number of strata and g = the number of groups (10 is the default). For the following example, we have 10 - 1 = 9 numerator degrees of freedom and 17 - 10 + 2 = 9 denominator degrees of freedom.
As of Stata 13.1, estat gof cannot follow a model specified with a subpopulation.
svy: logit paq665 i.female##c.pad680
(running logit on estimation sample)
Survey: Logistic regression
Number of strata = 14 Number of obs = 6742
Number of PSUs = 31 Population size = 255503942
Design df = 17
F( 3, 15) = 1.16
Prob > F = 0.3593
---------------------------------------------------------------------------------
| Linearized
paq665 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
----------------+----------------------------------------------------------------
female |
female | .1277199 .1276729 1.00 0.331 -.1416463 .3970861
pad680 | .0000791 .0002271 0.35 0.732 -.0004 .0005582
|
female#c.pad680 |
female | -.0003267 .0002309 -1.41 0.175 -.0008139 .0001605
|
_cons | -.1236965 .1246061 -0.99 0.335 -.3865923 .1391994
---------------------------------------------------------------------------------
estat gof
Logistic model for paq665, goodness-of-fit test
F(9,9) = 0.89
Prob > F = 0.5656
For more information on using the NHANES data sets
There are helpful resources for learning how to analyze the NHANES data sets correctly. One is a listserv at http://www.cdc.gov/nchs/nhanes/nhanes_listserv.htm . There are also online tutorials at http://www.cdc.gov/nchs/tutorials/index.htm .
References
Applied Survey Data Analysis by Steven G. Heeringa, Brady T. West, and Patricia A. Berglund
A survey of survey statistics: What is done and can be done in Stata by Frauke Kreuter and Richard Valliant, The Stata Journal (2007), Volume 7, Number 1, pages 1-21.
Goodness-of-fit test for a logistic regression model fitted using survey sample data by Kellie J. Archer and Stanley Lemeshow, The Stata Journal (2006), Volume 6, Number 1, pages 97-105.
Analysis of Health Surveys by Edward L. Korn and Barry I. Graubard
Sampling of Populations: Methods and Applications, Fourth Edition by Paul Levy and Stanley Lemeshow
Analysis of Survey Data Edited by R. L. Chambers and C. J. Skinner
Sampling Techniques, Third Edition by William G. Cochran
Stata 13 Manual: Survey Data