This page shows an example of a correlation with footnotes explaining the output. We have used the hsb2 data set for this example. The variables read, write, math and science are scores that 200 students received on these tests. The variable female is a 0/1 variable coded 1 if the student was female and 0 otherwise. We use this 0/1 variable to show that it is valid to use such a variable in a "regular" correlation.
When you use the correlation command in Stata, listwise deletion of missing data is done by default. When you do a listwise deletion, if a case has a missing value for any of the variables listed in the command, that case is eliminated from all correlations, even if there are valid values for the two variables in the current correlation. For example, if there was a missing value for the variable read, the case would still be excluded from the calculation of the correlation between write and math. This is why the number of observations is the same for all correlations and it can be printed at the top of the output.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2 (highschool and beyond (200 cases))
corr read write math science female
(obs=200)a
| read write math science female
-------------+---------------------------------------------
read | 1.0000b
write | 0.5968c 1.0000
math | 0.6623 0.6174 1.0000
science | 0.6302 0.5704 0.6307 1.0000
female | -0.0531d 0.2565 -0.0293 -0.1277 1.0000
a. This tells you the number of observations that were used in the correlations. In this data set, we have no missing values, so all correlations are based on all 200 observations.
b. This is the correlation between read and read. The correlation between any variable and itself is always 1.
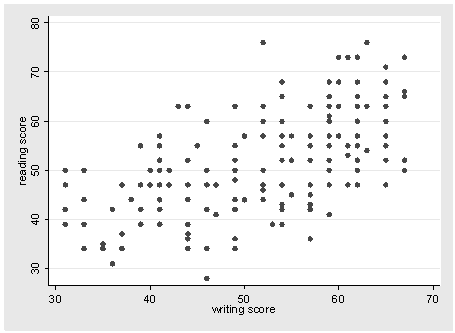
c. This is the correlation between write and read. It is positive, indicating that as one score increases, so does the other. Correlations measure the strength and direction of the linear relationship between the two variables. The correlation coefficient can range from -1 to +1, with -1 indicating a perfect negative correlation, +1 indicating a perfect positive correlation, and 0 indicating no correlation at all. (A variable correlated with itself will always have a correlation coefficient of 1.) You can think of the correlation coefficient as telling you the extent to which you can guess the value of one variable given a value of the other variable. From the scatterplot of the variables read and write below, we can see that the points tend along a line going from the bottom left to the upper right, which is the same as saying that the correlation is positive. The 597 is the numerical description of how tightly around the imaginary line the points lie. If the correlation was higher, the points would tend to be closer to the line; if it was smaller, they would tend to be further away from the line. Also note that, by definition, any variable correlated with itself has a correlation of 1.
d. This is the correlation between read and female. It is negative, indicating that as one score decreases, the other increases.
Pairwise deletion of missing data
The correlations in the table below are interpreted in the same way as those above. The only difference is the way the missing values are handled. When you do pairwise deletion, as we do in this example, a pair of data points are deleted from the calculation of the correlation only if one (or both) of the data points in that pair is missing.
There are really no rules defining when you should use pairwise or listwise deletion. It depends on your purpose and whether it is important for exactly the same cases to be used in all of the correlations. If you have lots of missing data, some correlations could be based on many cases that are not included in other correlations. On the other hand, if you use a listwise deletion, you may not have many cases left to be used in the calculation.
pwcorr read write math science female, obs
| read write math science female
-------------+---------------------------------------------
read | 1.0000
| 200
|
write | 0.5968a 1.0000
| 200b 200
|
math | 0.6623 0.6174 1.0000
| 200 200 200
|
science | 0.6302 0.5704 0.6307 1.0000
| 200 200 200 200
|
female | -0.0531 0.2565 -0.0293 -0.1277 1.0000
| 200 200 200 200 200
a. This is the correlation between read and write. It is positive, indicating that as the reading score increases, we expect that the writing score also increases.
b. This is the number of observations used in the calculation of the correlation.
Scatterplot
scatter read write