This page is Part 2 of a two-page sequence. If you have reached here without reading the first part you should go back because there is a lot of explanitory material that is not covered on this page. Go back now.
This page presents an approach for testing two-way interactions at each level of a third variable and for doing tests of simple main-effects on two-way interactions without having to copy the sums of squares and degrees of freedom and computing F-ratios manually.
As a review from the previous page we will look at the full three-factor anova along with the plots of the b*c interactions separately for a==1 and a==2.
use https://stats.idre.ucla.edu/stat/stata/faq/threeway, clear
anova y a b c a#b a#c b#c a#b#c
Number of obs = 24 R-squared = 0.9689
Root MSE = 1.1547 Adj R-squared = 0.9403
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 497.833333 11 45.2575758 33.94 0.0000
|
a | 150 1 150 112.50 0.0000
b | .666666667 1 .666666667 0.50 0.4930
c | 127.583333 2 63.7916667 47.84 0.0000
a#b | 160.166667 1 160.166667 120.12 0.0000
a#c | 18.25 2 9.125 6.84 0.0104
b#c | 22.5833333 2 11.2916667 8.47 0.0051
a#b#c | 18.5833333 2 9.29166667 6.97 0.0098
|
Residual | 16 12 1.33333333
-----------+----------------------------------------------------
Total | 513.833333 23 22.3405797
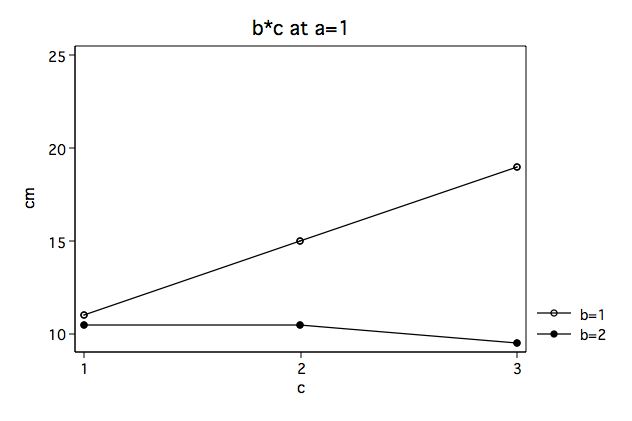
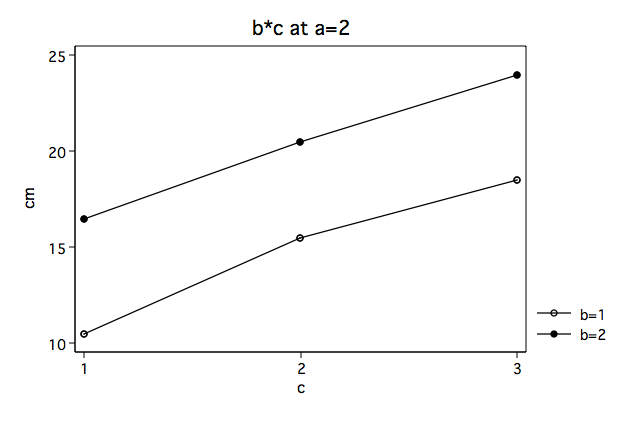
Again, we note that the b#c interaction looks very different at a==1 then at a==2.
Before we get into the alternative method of explaining the three-way interaction we will review effect-coding for variables b and c. In the table below, column (1) is the effect-coding for b main-effect; columns (2) and (4) are for the c main-effect; and columns (4) and (5) are for the b*c interaction.
Effect Coding
(1) (2) (3) (4) (5)
b c b c1 c2 bc1 bc2
1 1 1 1 0 1 0
1 2 1 0 1 0 1
1 3 1 -1 -1 -1 -1
2 1 -1 1 0 -1 0
2 2 -1 0 1 0 -1
2 3 -1 -1 -1 1 1
|
Next, we will run the anova model with b*c nested in a. You will note that the residual sums of squares and degrees of freedom are the same as for the original three factor model.
/* anova for b#c at levels of a */
anova y b c b#c|a
Number of obs = 24 R-squared = 0.9689
Root MSE = 1.1547 Adj R-squared = 0.9403
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 497.833333 11 45.2575758 33.94 0.0000
|
b | .666666667 1 .666666667 0.50 0.4930
c | 127.583333 2 63.7916667 47.84 0.0000
b#c|a | 369.583333 8 46.1979167 34.65 0.0000
|
Residual | 16 12 1.33333333
-----------+----------------------------------------------------
Total | 513.833333 23 22.3405797
If we use the test command with the showorder option, we can see what each of the parameters are.
test, showorder
Order of columns in the design matrix
1: (b==1)
2: (b==2)
3: (c==1)
4: (c==2)
5: (c==3)
6: (b==1)*(c==1)*(a==1)
7: (b==1)*(c==1)*(a==2)
8: (b==1)*(c==2)*(a==1)
9: (b==1)*(c==2)*(a==2)
10: (b==1)*(c==3)*(a==1)
11: (b==1)*(c==3)*(a==2)
12: (b==2)*(c==1)*(a==1)
13: (b==2)*(c==1)*(a==2)
14: (b==2)*(c==2)*(a==1)
15: (b==2)*(c==2)*(a==2)
16: (b==2)*(c==3)*(a==1)
17: (b==2)*(c==3)*(a==2)
18: _cons
From the table above we can see that the b*c interaction for each level of a are found in rows 7 through 18. We will use the effect-coding from columns (4) and (5) above aligned with the appropriate element of matrices bc1 and bc2 to test the interaction separately at each level of a. For example, the -1’s in column (4) are found when b==1 & c==1 and when b==2 & c==1. For the case when a==1 in the showorder these vales occur in row 11 and row 13. The matrices used with the test are created using the column to represent the parameter, so in the first row of bc1 columns 11 and 13 will have -1’s. The two rows of bc1 test the b*c interaction at a==1, while bc2 tests the interaction at a==2.
matrix bc1=(0,0,0,0,0,0,1,0,0,0,-1,0,-1,0,0,0,1,0 ///
0,0,0,0,0,0,0,0,1,0,-1,0,0,0,-1,0,1,0)
matrix list bc1
bc1[2,18]
c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c13 c14 c15 c16 c17 c18
r1 0 0 0 0 0 0 1 0 0 0 -1 0 -1 0 0 0 1 0
r2 0 0 0 0 0 0 0 0 1 0 -1 0 0 0 -1 0 1 0
matrix bc2=(0,0,0,0,0,0,1,0,0,0,-1,0,-1,0,0,0,1,0 ///
0,0,0,0,0,0,0,0,1,0,-1,0,0,0,-1,0,1,0)
matrix list bc2
bc2[2,18]
c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c13 c14 c15 c16 c17 c18
r1 0 0 0 0 0 0 1 0 0 0 -1 0 -1 0 0 0 1 0
r2 0 0 0 0 0 0 0 0 1 0 -1 0 0 0 -1 0 1 0
Next, using the test command with the test() option we test the interactions.
/* test b#c at a==1 */
test, test(bc1)
( 1) 1b.b#1b.c|1b.a - 1b.b#3o.c|1b.a - 2o.b#1b.c|1b.a + 2.b#3.c|1b.a = 0
( 2) 1b.b#2o.c|1b.a - 1b.b#3o.c|1b.a - 2.b#2.c|1b.a + 2.b#3.c|1b.a = 0
F( 2, 12) = 15.25
Prob > F = 0.0005
/* test b#c at a==2 */
test, test(bc2)
( 1) 1b.b#1b.c|2.a - 1b.b#3.c|2.a - 2.b#1b.c|2.a + 2.b#3.c|2.a = 0
( 2) 1b.b#2.c|2.a - 1b.b#3.c|2.a - 2.b#2.c|2.a + 2.b#3.c|2.a = 0
F( 2, 12) = 0.19
Prob > F = 0.8314
return list /* to see the F-ratio to more decimal places */
scalars:
r(p) = .8314118892405915
r(df) = 2
r(F) = .1874999999999936
r(df_r) = 12
r(drop) = 0
These are the same two F-ratios (15.25 and .1875) that we computed using the original method in Part 1. And, just as in Part 1, we need to use the appropriate critical values for the F-ratios and not just go by the printed p-values.
Now that we know that the b*c interaction at a==1 is sifnificant, we can move on to testing whether there are significant difference in the levels of c for each of the levels of b at a==1. To accomplish this we will run another anova model, this time looking a c nested in a*b. Once again, please note, that the residual SS and df are the same as the original three factor model.
/* anova for testing c holding a & b constant */
anova y c|a#b
ova y c|a#b
Number of obs = 24 R-squared = 0.9689
Root MSE = 1.1547 Adj R-squared = 0.9403
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 497.833333 11 45.2575758 33.94 0.0000
|
c|a#b | 497.833333 11 45.2575758 33.94 0.0000
|
Residual | 16 12 1.33333333
-----------+----------------------------------------------------
Total | 513.833333 23 22.3405797
Let’s run test with the showorder option for this model.
test, showorder
Order of columns in the design matrix
1: (c==1)*(a==1)*(b==1)
2: (c==1)*(a==1)*(b==2)
3: (c==1)*(a==2)*(b==1)
4: (c==1)*(a==2)*(b==2)
5: (c==2)*(a==1)*(b==1)
6: (c==2)*(a==1)*(b==2)
7: (c==2)*(a==2)*(b==1)
8: (c==2)*(a==2)*(b==2)
9: (c==3)*(a==1)*(b==1)
10: (c==3)*(a==1)*(b==2)
11: (c==3)*(a==2)*(b==1)
12: (c==3)*(a==2)*(b==2)
13: _cons
Using the effect-coding columns (2) and (3) from above, we will create two more test matrices aligning the parameters with the c main-effect. This time there will only be 13 columns in each matrix.
matrix c1=(1,0,0,0,0,0,0,0,-1,0,0,0,0 ///
0,0,0,0,1,0,0,0,-1,0,0,0,0)
matrix list c1
c1[2,13]
c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c13
r1 1 0 0 0 0 0 0 0 -1 0 0 0 0
r2 0 0 0 0 1 0 0 0 -1 0 0 0 0
matrix c2=(0,0,1,0,0,0,0,0,0,0,-1,0,0 ///
0,0,0,0,0,0,1,0,0,0,-1,0,0)
matrix list c2
c2[2,13]
c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c13
r1 0 1 0 0 0 0 0 0 0 -1 0 0 0
r2 0 0 0 0 0 1 0 0 0 -1 0 0 0
We can now go to the test commands themselves.
/* test for c at a==1 & b==1 */
test, test(c1)
( 1) 1b.c|1b.a#1b.b - 3.c|1b.a#1b.b = 0
( 2) 2.c|1b.a#1b.b - 3.c|1b.a#1b.b = 0
F( 2, 12) = 24.00
Prob > F = 0.0001
/* test for c at a==1 & b==2 */
test, test(c2)
( 1) 1b.c|1b.a#2.b - 3.c|1b.a#2.b = 0
( 2) 2.c|1b.a#2.b - 3.c|1b.a#2.b = 0
F( 2, 12) = 0.50
Prob > F = 0.6186
Once again, these F-ratios (24.0 and 0.50) are the same as those computed using the method in Part 1. And, as in Part 1, we would have to finish up by running pair-wise comparisons among the means at a==1, b==1. We can run the same tukeyhsd command as we did before.
Just a word of warning. You won’t be able to cut-and-paste the Stata commands from this page, like the previous page, because it is unlikely that your model will follow the same patterns of levels and effects as this example. It will be necessary that you work out the correct coding for each research project individually.
References
Kirk, Roger E. (1995) Experimental Design: Procedures for the Behavioral Sciences, Third Edition. Monterey, California: Brooks/Cole Publishing.
