First off, let’s start with what a significant three-way interaction means. It means that there is a two-way interaction that varies across levels of a third variable. Say, for example, that a b*c interaction differs across various levels of factor a.
One way of analyzing the three-way interaction is to begin by testing two-way interactions at each level of a third variable. This process is just a generalization of tests of simple main effects which can is used for two-way interactions. If you find the material on this FAQ page to be confusing there is another page which takes a more conceptual approach that is not stat package specific. That page is located here.
We will use a small artificial example that has a statistically significant three-way interaction to illustrate the process.
use https://stats.idre.ucla.edu/stat/stata/faq/threeway, clear
anova y a b c a*b a*c b*c a*b*c
Number of obs = 24 R-squared = 0.9689
Root MSE = 1.1547 Adj R-squared = 0.9403
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 497.833333 11 45.2575758 33.94 0.0000
|
a | 150 1 150 112.50 0.0000
b | .666666667 1 .666666667 0.50 0.4930
c | 127.583333 2 63.7916667 47.84 0.0000
a*b | 160.166667 1 160.166667 120.13 0.0000
a*c | 18.25 2 9.125 6.84 0.0104
b*c | 22.5833333 2 11.2916667 8.47 0.0051
a*b*c | 18.5833333 2 9.29166667 6.97 0.0098
|
Residual | 16 12 1.33333333
-----------+----------------------------------------------------
Total | 513.833333 23 22.3405797
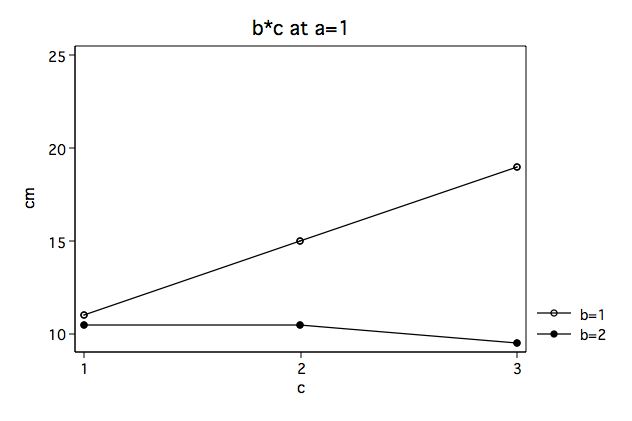
Next, we need to select a two-way interaction to look at more closely. For the purposes of this example we will examine the b*c interaction. Let’s graph the b*c interaction for each of the two levels of a. We will do this by computing the cell means for the 12 cells in the design.
egen abc=group(a b c), label
egen cm=mean(y), by(abc)
twoway (connect cm c if a==1 & b==1)(connect cm c if a==1 & b==2), ///
name(at_a_1) xlabel(1(1)3) title("b*c at a=1") ///
ylabel(10(5)25) legend(order(1 "b=1" 2 "b=2"))
 twoway (connect cm c if a==2 & b==1)(connect cm c if a==2 & b==2), ///
name(at_a_2) xlabel(1(1)3) title("b*c at a=2") ///
ylabel(10(5)25) legend(order(1 "b=1" 2 "b=2"))
twoway (connect cm c if a==2 & b==1)(connect cm c if a==2 & b==2), ///
name(at_a_2) xlabel(1(1)3) title("b*c at a=2") ///
ylabel(10(5)25) legend(order(1 "b=1" 2 "b=2"))
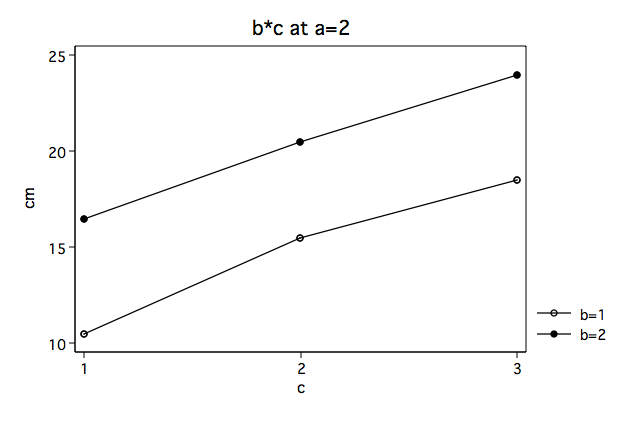
We believe from looking at the two graphs above that the three-way interaction is significant because there appears to be a “strong” two-way interaction at a = 1 and no interaction at a = 2. Now, we just have to show it statistically using tests of simple main-effects. To do that we will make use of a user-written Stata command testalterr. You can find the testalterr program by typing search testalterr in the Stata command window (see How can I use the search command to search for programs and get additional help? for more information about using search). In addition, you will need to keep track of the residual sum of squares and degrees of freedom from the original 2x2x3 factorial anova (rss=16 and dfr=12).
We will begin by running a two-way anova with b and c at a=1. This two-way anova uses the wrong error the to test b*c within a1 so we will use testalterr to test the effect using the correct error term.
/* run anova model with b & c at a==1 */
anova y b c b*c if a==1
Number of obs = 12 R-squared = 0.9475
Root MSE = 1.11803 Adj R-squared = 0.9038
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 135.416667 5 27.0833333 21.67 0.0009
|
b | 70.0833333 1 70.0833333 56.07 0.0003
c | 24.6666667 2 12.3333333 9.87 0.0127
b*c | 40.6666667 2 20.3333333 16.27 0.0038
|
Residual | 7.5 6 1.25
-----------+----------------------------------------------------
Total | 142.916667 11 12.9924242
/* test using error term from original anova */
testalterr b*c, rss(16) dfr(12)
Test of b*c using alternate error term (1.3333333)
F(2,12) = 15.25 p-value = .0005067
The F-ratio of 15.25 is the test of the b*c interaction at a = 1. We will defer the discussion on the critical value for a few moments while we compute the test of simple interaction-effect at a = 2.
anova y b c b*c if a==2
Number of obs = 12 R-squared = 0.9615
Root MSE = 1.19024 Adj R-squared = 0.9295
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 212.416667 5 42.4833333 29.99 0.0004
|
b | 90.75 1 90.75 64.06 0.0002
c | 121.166667 2 60.5833333 42.76 0.0003
b*c | .5 2 .25 0.18 0.8424
|
Residual | 8.5 6 1.41666667
-----------+----------------------------------------------------
Total | 220.916667 11 20.0833333
/* test using error term from original anova */
testalterr b*c, rss(16) dfr(12)
Test of b*c using alternate error term (1.3333333)
F(2,12) = .1875 p-value = .83141189
Clearly, one F-ratio is much larger than the other but how can we tell which are statistically significant? There are at least four different methods of determining the critical value of tests of simple main-effects. There is a method related to Dunn’s multiple comparisons, a method attributed to Marascuilo & Levin, a method called the simultaneous test procedure (very conservative and related to the Scheffé post-hoc test) and a per family error rate method.
We will demonstrate the per family error rate method but you should look up the other methods in a good anova book, like Kirk (1995), to decide which approach is best for your situation. The trick here is that we divide 0.05, our alpha level, by 2 in the invfprob function because we are doing two tests of simple main-effects.
/* compute critical value */ display "critical value per family error rate = " invfprob(2, 12, 0.05/2) critical value per family error rate = 5.0958672
The critical value is approximately 5.1. The first F-ratio of 15.25 is significant while the second (.1875) is not. In other words, the two-way b*c interaction is significant at a = 1 but is not significant at a = 2.
In an ideal world we would be done now, but since we live in the “real” world, there is still more to do because we now need to try to understand the significant two-way interaction at a = 1; first for b = 1 and then for b = 2.
/* look at differences in c at b==1 when a==1 */
anova y c if b==1 & a==1
Number of obs = 6 R-squared = 0.9143
Root MSE = 1.41421 Adj R-squared = 0.8571
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 64 2 32 16.00 0.0251
|
c | 64 2 32 16.00 0.0251
|
Residual | 6 3 2
-----------+----------------------------------------------------
Total | 70 5 14
testalterr c, rss(16) dfr(12)
Test of c using alternate error term (1.3333333)
F(2,12) = 24 p-value = .000064
/* look at differences in c at b==2 when a==1 */
anova y c if b==2 & a==1
Number of obs = 6 R-squared = 0.4706
Root MSE = .707107 Adj R-squared = 0.1176
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 1.33333333 2 .666666667 1.33 0.3852
|
c | 1.33333333 2 .666666667 1.33 0.3852
|
Residual | 1.5 3 .5
-----------+----------------------------------------------------
Total | 2.83333333 5 .566666667
testalterr c, rss(16) dfr(12)
Test of c using alternate error term (1.3333333)
F(2,12) = .5 p-value = .61862485
/* compute critical value */
display "critical value per family error rate = " invfprob(2, 12, 0.05/2)
critical value per family error rate = 5.0958672
Only the test of simple main-effects of c at b = 1 was significant. But we’re not done yet, since there are three levels of c, we don’t know where this significant effect lies. We need to test the pairwise comparisons among the three means. We will do this using the tukeyhsd command (search tukeyhsd; see How can I use the search command to search for programs?) for our pairwise comparisons. We use an if in the tukeyhsd command to restrict the pairwise comparisons to b = 1 at a = 1.
/* all pairwise comparisons at a==1 & b==1 */ tukeyhsd c if a==1 & b==1, nu(12) mse(1.3333333) Tukey HSD pairwise comparisons for variable c studentized range critical value(.05, 3, 12) = 3.772768 uses harmonic mean sample size = 2.000 mean grp vs grp group means dif HSD-test ------------------------------------------------------- 1 vs 2 11.0000 15.0000 4.0000 4.8990* 1 vs 3 11.0000 19.0000 8.0000 9.7980* 2 vs 3 15.0000 19.0000 4.0000 4.8990*
As shown above, each of the pairwise comparisons among the levels of c at b = 1 are statistically significant. Hopefully, we now have a much better understanding of the three-way a*b*c interaction.
The process would have be similar if we had chosen a different two-way interaction back at the beginning.
Summary of Steps
1) Run full model with three-way interaction.
1a) Capture SS and df residual.
2) Run two-way interaction at each level of third variable.
2a) Compute F-ratios using testalterr to test 2-way interactions at levels of a 3rd variable.
3) Run one-way model at each level of second variable.
3a) Compute F-ratios using testalterr to test simple main-effects.
4) Run pairwise or other post-hoc comparisons if necessary
Is there some way of computing the various F-ratios for understanding the 3-way interaction without using running separate anovas and using testalterr? Yes, there is. Is it easier that the method above? No, its just different. Click on Part 2 to view it.
References
Kirk, Roger E. (1995) Experimental Design: Procedures for the Behavioral Sciences, Third Edition. Monterey, California: Brooks/Cole Publishing.
