Let’s begin with with what a significant three-way interaction means. It means that there is a two-way interaction that varies across levels of a third variable. Say, for example, that a b#c interaction differs across various levels of factor a.
One way of analyzing the three-way interaction is to begin by testing two-way interactions at each level of a third variable. This process is just a generalization of tests of simple effects which can is used for two-way interactions. If you find the material on this FAQ page to be confusing there is another page which takes a more conceptual approach that is not stat package specific. That page is located here.
We will use a small artificial example that has a statistically significant three-way interaction to illustrate the process.
use https://stats.idre.ucla.edu/stat/stata/faq/threeway, clear
anova y a##b##c
Number of obs = 24 R-squared = 0.9689
Root MSE = 1.1547 Adj R-squared = 0.9403
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 497.833333 11 45.2575758 33.94 0.0000
|
a | 150 1 150 112.50 0.0000
b | .666666667 1 .666666667 0.50 0.4930
c | 127.583333 2 63.7916667 47.84 0.0000
a#b | 160.166667 1 160.166667 120.12 0.0000
a#c | 18.25 2 9.125 6.84 0.0104
b#c | 22.5833333 2 11.2916667 8.47 0.0051
a#b#c | 18.5833333 2 9.29166667 6.97 0.0098
|
Residual | 16 12 1.33333333
-----------+----------------------------------------------------
Total | 513.833333 23 22.3405797
Next, we’ll look at the cell means using the margins command.
margins a#b#c
Adjusted predictions Number of obs = 24
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
a#b#c |
1 1 1 | 11 .8164966 13.47 0.000 9.399696 12.6003
1 1 2 | 15 .8164966 18.37 0.000 13.3997 16.6003
1 1 3 | 19 .8164966 23.27 0.000 17.3997 20.6003
1 2 1 | 10.5 .8164966 12.86 0.000 8.899696 12.1003
1 2 2 | 10.5 .8164966 12.86 0.000 8.899696 12.1003
1 2 3 | 9.5 .8164966 11.64 0.000 7.899696 11.1003
2 1 1 | 10.5 .8164966 12.86 0.000 8.899696 12.1003
2 1 2 | 15.5 .8164966 18.98 0.000 13.8997 17.1003
2 1 3 | 18.5 .8164966 22.66 0.000 16.8997 20.1003
2 2 1 | 16.5 .8164966 20.21 0.000 14.8997 18.1003
2 2 2 | 20.5 .8164966 25.11 0.000 18.8997 22.1003
2 2 3 | 24 .8164966 29.39 0.000 22.3997 25.6003
------------------------------------------------------------------------------
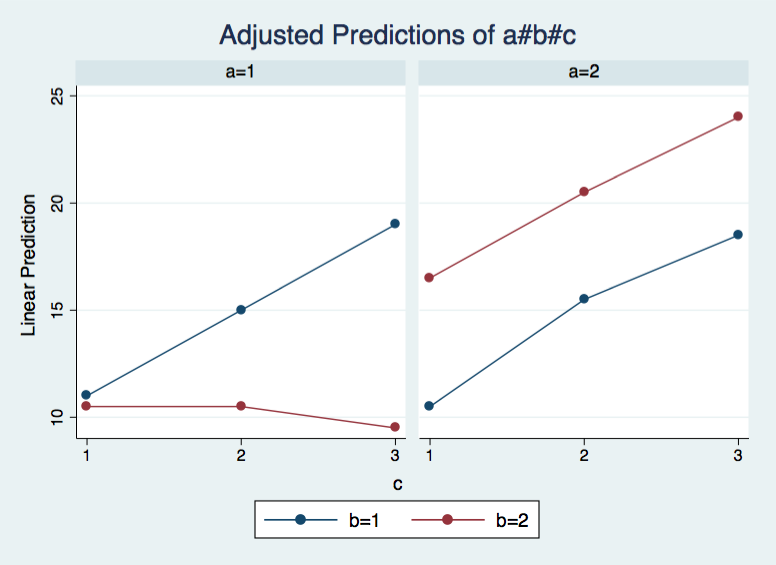
Next, we will plot the cells means to see which effects look promising to follow up on. The marginsplot command will do the job for us.
marginsplot, by(a) x(c) noci
We believe from looking at the graph above that the three-way interaction is significant because there appears to be a “strong” two-way interaction at a = 1 and no interaction at a = 2. Now, we just have to show it statistically using tests of simple effects. To do this we will use the contrast command. The b#a@a, in the command, looks a little strange but it is just requesting the b#c interaction effect for each level of variable a.
contrast b#c@a
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
b#c@a |
1 | 2 15.25 0.0005
2 | 2 0.19 0.8314
Joint | 4 7.72 0.0026
|
Residual | 12
------------------------------------------------
The F-ratio for the b#c interaction at a = 1 is 15.25, while the F-ratio for the b#c at a =2 is 0.19. The p-values given in the table have not been adjusted for these post-hoc multiple comparisons. This is a topic we need to discuss.
Clearly, one F-ratio is much larger than the other but how can we tell which are statistically significant? There are at least four different methods of determining the critical value of tests of simple main-effects. There is a method related to Dunn’s multiple comparisons, a method attributed to Marascuilo & Levin, a method called the simultaneous test procedure (very conservative and related to the Scheffé post-hoc test) and a per family error rate method.
We will demonstrate the per family error rate method but you should look up the other methods in a good anova book, like Kirk (1995), to decide which approach is best for your situation. The trick here is that we divide 0.05, our alpha level, by 2 in the invfprob function because we are doing two tests of simple main-effects.
/* compute critical value */ display "critical value per family error rate = " invfprob(2, 12, 0.05/2) critical value per family error rate = 5.0958672
The critical value is approximately 5.1. The first F-ratio of 15.25 is significant while the second (.1875) is not. In other words, the two-way b#c interaction is significant at a = 1 but is not significant at a = 2.
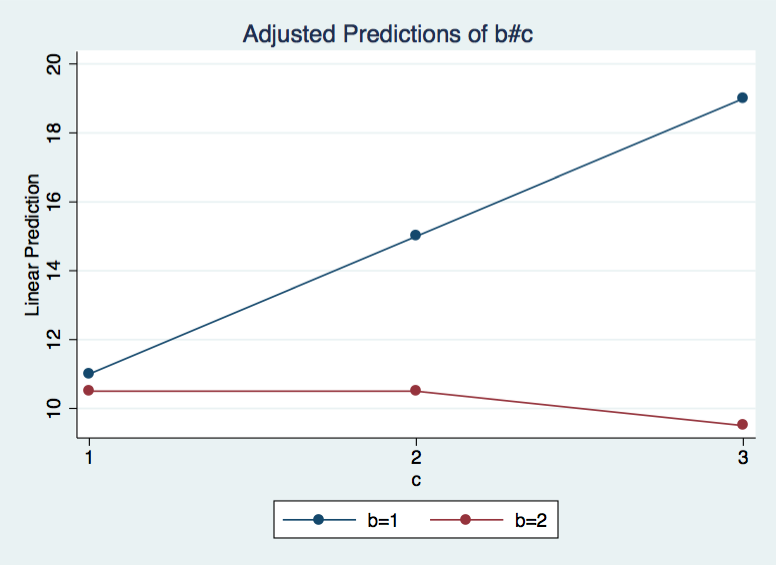
In an ideal world we would be done now, but since we live in the “real” world, there is still more to do because we now need to try to understand the significant two-way interaction at a = 1; first for b = 1 and then for b = 2. Let’s remake the plot of the cell means for b and c at a = 1.
margins b#c, at(a=1)
Adjusted predictions Number of obs = 24
Expression : Linear prediction, predict()
at : a = 1
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
b#c |
1 1 | 11 .8164966 13.47 0.000 9.399696 12.6003
1 2 | 15 .8164966 18.37 0.000 13.3997 16.6003
1 3 | 19 .8164966 23.27 0.000 17.3997 20.6003
2 1 | 10.5 .8164966 12.86 0.000 8.899696 12.1003
2 2 | 10.5 .8164966 12.86 0.000 8.899696 12.1003
2 3 | 9.5 .8164966 11.64 0.000 7.899696 11.1003
------------------------------------------------------------------------------
marginsplot, x(c) noci
To perform the next test we could use the margins command with the contrast option. Here’s what it looks like.
margins c@b, at(a=1) contrast
Contrasts of adjusted predictions
Expression : Linear prediction, predict()
at : a = 1
------------------------------------------------
| df chi2 P>chi2
-------------+----------------------------------
c@b |
1 | 2 48.00 0.0000
2 | 2 1.00 0.6065
Joint | 4 49.00 0.0000
------------------------------------------------
You will note that the margins, contrast command displays the test statistic as a chi-square not as an F-ratio. If we use the contrast command the test statistic will be scaled as an F-ratio. The trick to getting the command to work for this analysis is to use the @ symbol twice, once with b and once with i(1).a.
contrast c@b@i(1).a
Contrasts of marginal linear predictions
Margins : asbalanced
------------------------------------------------
| df F P>F
-------------+----------------------------------
c@b#a |
1 1 | 2 24.00 0.0001
2 1 | 2 0.50 0.6186
Joint | 4 12.25 0.0003
|
Denominator | 12
------------------------------------------------
Only the test of simple effects of c at b = 1 was statistically significant. But we’re not done yet, since there are three levels of c, we don’t know where this significant effect lies. We need to test the pairwise comparisons among the three means when b = 1 and a = 1. We will do this using the the pwcompare command (introduced in Stata 12) with the mcompare(tukey) and effect options.
pwcompare c#i(1).b#i(1).a, mcompare(tukey) effects
Pairwise comparisons of marginal linear predictions
Margins : asbalanced
---------------------------
| Number of
| Comparisons
-------------+-------------
c#b#a | 3
---------------------------
-------------------------------------------------------------------------------------
| Tukey Tukey
| Contrast Std. Err. t P>|t| [95% Conf. Interval]
--------------------+----------------------------------------------------------------
c#b#a |
(2 1 1) vs (1 1 1) | 4 1.154701 3.46 0.012 .9194165 7.080584
(3 1 1) vs (1 1 1) | 8 1.154701 6.93 0.000 4.919416 11.08058
(3 1 1) vs (2 1 1) | 4 1.154701 3.46 0.012 .9194165 7.080584
-------------------------------------------------------------------------------------
From the table above, it appears that all three of the pairwise comparisons are statistically significant.
The process would have be similar if we had chosen a different two-way interaction back at the beginning.
One final note, all of the commands shown on this page work exactly the same if we had run the model using regress instead of anova.
Summary of Steps
1) Run full model with three-way interaction. 1a) Capture SS and df residual. 2) Run two-way interaction at each level of third variable. 2a) Capture SS and df for interactions. 2b) Compute F-ratios for tests of interaction at levels of a 3rd variable. 3) Run one-way model at each level of second variable. 3a) Capture SS and df for main effects. 3b) Compute F-ratios for tests of simple main-effects. 4) Run pairwise or other post-hoc comparisons if necessary
References
Kirk, Roger E. (1995) Experimental Design: Procedures for the Behavioral Sciences, Third Edition. Monterey, California: Brooks/Cole Publishing.