Interactions in logistic regression models can be trickier than interactions in comparable OLS regression models. This is particularly true when there are covariates in the model in addition to the categorical predictors. This FAQ page will try to help you to understand categorical by categorical interactions in logistic regression models with continuous covariates.
We will use an example dataset, logit2-2, that has two binary predictors, f and h, and a continuous covariate, cv1. In addition, the model will include f by h interaction. We will begin by loading the data, creating the interaction variable and running the logit model.
use https://stats.idre.ucla.edu/stat/data/logit2-2, clear
logit y f##h cv1
Logistic regression Number of obs = 200
LR chi2(4) = 106.10
Prob > chi2 = 0.0000
Log likelihood = -78.74193 Pseudo R2 = 0.4025
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.f | 2.996118 .7521524 3.98 0.000 1.521926 4.470309
1.h | 2.390911 .6608498 3.62 0.000 1.09567 3.686153
|
f#h |
1 1 | -2.047755 .8807989 -2.32 0.020 -3.774089 -.3214213
|
cv1 | .196476 .0328518 5.98 0.000 .1320876 .2608644
_cons | -11.86075 1.895828 -6.26 0.000 -15.5765 -8.144991
------------------------------------------------------------------------------
As you can see all of the variables in the above model including the interaction term are statistically significant. If this were an OLS regression model we could do a very good job of understanding the interaction using just the coefficients in the model. The situation in logistic regression is more complicated because the effect of the covariate is nonlinear, meaning that the interaction effect can be very different for different values of the covariate. To begin to understand what is going on consider the Table 1 below.
Table 1: Predicted probabilities when cv1=50
h=0 h=1 Dprob LB UB
f=0 .1154 .5876 .4722 .2693 .6751
f=1 .7230 .7862 .0633 -.1399 .2665
Table 1 contain predicted probabilities, differences in predicted probabilities and the confidence interval of the difference in predicted probabilities while holding cv1 at 50. The first value, .1154, is the predicted probability when f=0 and h=0. The second value, .5876, is the predicted probability when f=0 and h=1. The third value, .4722, is the difference in probabilities for f=0 when h changes from 0 to 1. The next two values are the 95% confidence interval on the difference in probabilities. If the confidence interval contains zero the difference would not be considered statistically significant. In our example, the confidence interval does not contain zero. Thus, for our example, the difference in probabilities is statistically significant.
We we can obtained all the values for Table 1 for a range of values of cv1 by using the margins command twice. We run margins once to get the probabilities for h = 0 and h = 1 for both f equal 0 and 1.
margins h, at(f=(0 1) cv1=(30(5)70)) vsquish
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
1._at : f = 0
cv1 = 30
2._at : f = 0
cv1 = 35
3._at : f = 0
cv1 = 40
4._at : f = 0
cv1 = 45
5._at : f = 0
cv1 = 50
6._at : f = 0
cv1 = 55
7._at : f = 0
cv1 = 60
8._at : f = 0
cv1 = 65
9._at : f = 0
cv1 = 70
10._at : f = 1
cv1 = 30
11._at : f = 1
cv1 = 35
12._at : f = 1
cv1 = 40
13._at : f = 1
cv1 = 45
14._at : f = 1
cv1 = 50
15._at : f = 1
cv1 = 55
16._at : f = 1
cv1 = 60
17._at : f = 1
cv1 = 65
18._at : f = 1
cv1 = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#h |
1 0 | .0025567 .0025254 1.01 0.311 -.0023929 .0075063
1 1 | .0272372 .0206496 1.32 0.187 -.0132352 .0677097
2 0 | .0067995 .0057853 1.18 0.240 -.0045396 .0181385
2 1 | .069579 .0413211 1.68 0.092 -.0114088 .1505668
3 0 | .0179561 .0129716 1.38 0.166 -.0074678 .04338
3 1 | .1664783 .0709412 2.35 0.019 .0274362 .3055204
4 0 | .0465604 .028158 1.65 0.098 -.0086283 .101749
4 1 | .3478701 .0933387 3.73 0.000 .1649296 .5308105
5 0 | .115378 .0575106 2.01 0.045 .0026592 .2280968 value from Table 1
5 1 | .5875788 .0877652 6.69 0.000 .4155621 .7595955 value from Table 1
6 0 | .2583492 .1025789 2.52 0.012 .0572982 .4594002
6 1 | .7918883 .0631887 12.53 0.000 .6680407 .9157359
7 0 | .4819613 .1389465 3.47 0.001 .209631 .7542915
7 1 | .910416 .037977 23.97 0.000 .8359824 .9848496
8 0 | .7130398 .1272483 5.60 0.000 .4636377 .9624418
8 1 | .9644667 .0200004 48.22 0.000 .9252666 1.003667
9 0 | .8690487 .0818878 10.61 0.000 .7085515 1.029546
9 1 | .9863932 .0096629 102.08 0.000 .9674543 1.005332
10 0 | .0487835 .0294567 1.66 0.098 -.0089504 .1065175
10 1 | .0674087 .0446964 1.51 0.132 -.0201947 .1550121
11 0 | .1204719 .0549249 2.19 0.028 .0128212 .2281227
11 1 | .1618113 .07791 2.08 0.038 .0091104 .3145121
12 0 | .267844 .0851192 3.15 0.002 .1010134 .4346747
12 1 | .3401934 .1024706 3.32 0.001 .1393547 .5410321
13 0 | .4941981 .1006298 4.91 0.000 .2969673 .6914289
13 1 | .5793115 .0914477 6.33 0.000 .4000773 .7585456
14 0 | .7229559 .0872338 8.29 0.000 .5519808 .8939309 value from Table 1
14 1 | .7862264 .0599327 13.12 0.000 .6687605 .9036924 value from Table 1
15 0 | .8745225 .0571538 15.30 0.000 .762503 .986542
15 1 | .9076026 .034318 26.45 0.000 .8403406 .9748645
16 0 | .9490168 .0308608 30.75 0.000 .8885308 1.009503
16 1 | .9632823 .0180954 53.23 0.000 .9278159 .9987487
17 0 | .9802821 .0149266 65.67 0.000 .9510265 1.009538
17 1 | .985929 .0088829 110.99 0.000 .9685188 1.003339
18 0 | .992525 .006799 145.98 0.000 .9791993 1.005851
18 1 | .9946848 .0041367 240.46 0.000 .986577 1.002792
------------------------------------------------------------------------------
Using the marginsplot command we can graph the predicted probabilities for each of the four cells in the design for various values of the covariate.
marginsplot, x(cv1)
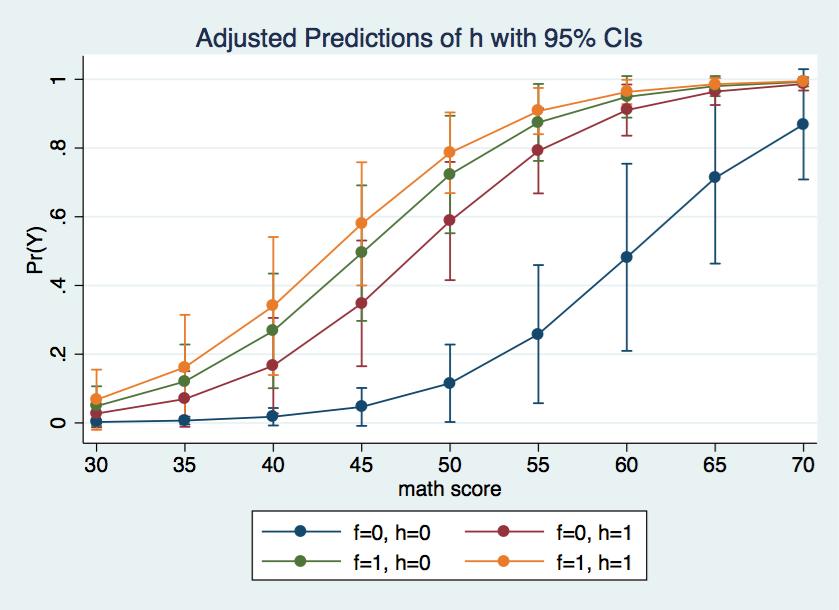
The graph above shows the f = 0, h = 0 cell is rather different from the other three cells.
Next, we will run margins again to get the difference in probabilities and them confidence interval for the difference. We will manually annotate the output to indicate which values are the same as Table 1.
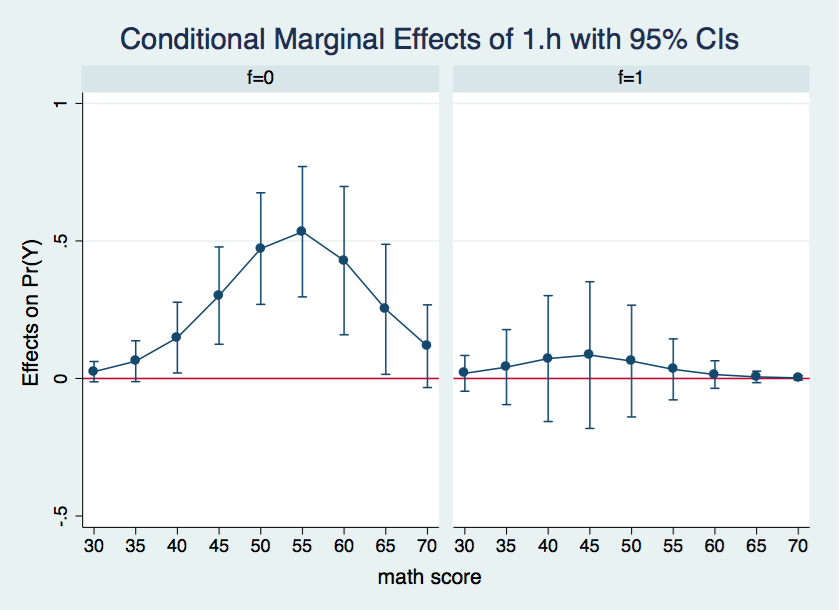
margins f, dydx(h) at(cv1=(30(5)70)) vsquish
Conditional marginal effects Number of obs = 200
Model VCE : OIM
Expression : Pr(y), predict()
dy/dx w.r.t. : 1.h
1._at : cv1 = 30
2._at : cv1 = 35
3._at : cv1 = 40
4._at : cv1 = 45
5._at : cv1 = 50
6._at : cv1 = 55
7._at : cv1 = 60
8._at : cv1 = 65
9._at : cv1 = 70
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.h |
_at#f |
1 0 | .0246805 .0188412 1.31 0.190 -.0122475 .0616086
1 1 | .0186252 .0331697 0.56 0.574 -.0463863 .0836367
2 0 | .0627795 .0378532 1.66 0.097 -.0114115 .1369704
2 1 | .0413394 .0695885 0.59 0.552 -.0950517 .1777304
3 0 | .1485222 .0656193 2.26 0.024 .0199107 .2771337
3 1 | .0723494 .1167547 0.62 0.535 -.1564856 .3011843
4 0 | .3013097 .0902579 3.34 0.001 .1244074 .478212
4 1 | .0851134 .1360832 0.63 0.532 -.1816048 .3518315
5 0 | .4722008 .1035128 4.56 0.000 .2693194 .6750821 value from Table 1
5 1 | .0632706 .1036697 0.61 0.542 -.1399183 .2664595 value from Table 1
6 0 | .5335391 .1208833 4.41 0.000 .2966122 .7704659
6 1 | .0330801 .0565538 0.58 0.559 -.0777632 .1439234
7 0 | .4284548 .137549 3.11 0.002 .1588636 .6980459
7 1 | .0142654 .0255894 0.56 0.577 -.0358888 .0644197
8 0 | .2514269 .120641 2.08 0.037 .014975 .4878788
8 1 | .0056469 .0106397 0.53 0.596 -.0152065 .0265003
9 0 | .1173445 .076704 1.53 0.126 -.0329926 .2676816
9 1 | .0021597 .0042758 0.51 0.613 -.0062207 .0105402
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
Here is what we can say based upon the output above. There are no significant differences between the two levels of h when the covariate is held constant at either 30 or 35. When the covariate is held constant between 40 and 65 there is a significant h 0-1 difference at f=0 but not at f=1. Finally, when the covariates are held constant at 70 the h differences are not significant. It may be easier to understand these results if we graph the confidence intervals for the difference in probability separately for both f=0 and f=1.
There is so much information in the margins output that its difficult to see what is going on. A graphic representation would do a better job of organizing and displaying the results. We will produce the graphs using using the marginsplot command once again.
marginsplot, x(cv1) by(f) yline(0)
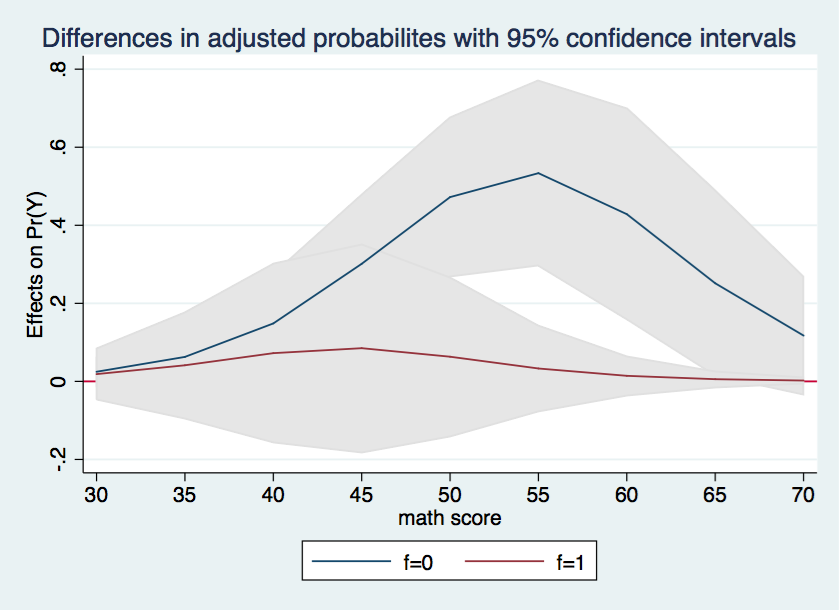
Wherever the confidence interval includes zero the differences in the adjusted probabilities between h = 0 and h = 1 is not statistically significant. This is the case for all of the data points in the graph for f = 1. On the other hand, for f = 0, all of the differences in probabilities between cv1 = 40 and 65 appear to be significant.
Finally, we will try to combine the two halves of the graph into a single graph with shaded confidence intervals. There is no new information here, we are just aiming at a more visually interesting graph.
marginsplot, recast(line) recastci(rarea) ciopts(color(gs14)) x(cv1) yline(0) ///
title(Differences in adjusted probabilites with 95% confidence intervals)