Consider the following xtmelogit.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
xtmelogit honors i.female read || cid:
Refining starting values:
Iteration 0: log likelihood = -82.156921
Iteration 1: log likelihood = -80.132249
Iteration 2: log likelihood = -79.765159
Performing gradient-based optimization:
Iteration 0: log likelihood = -79.765159
Iteration 1: log likelihood = -79.721813
Iteration 2: log likelihood = -79.72173
Iteration 3: log likelihood = -79.72173
Mixed-effects logistic regression Number of obs = 200
Group variable: cid Number of groups = 20
Obs per group: min = 7
avg = 10.0
max = 12
Integration points = 7 Wald chi2(2) = 6.39
Log likelihood = -79.72173 Prob > chi2 = 0.0410
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.female | 1.203685 .498816 2.41 0.016 .2260232 2.181346
read | .0426387 .0579243 0.74 0.462 -.0708908 .1561682
_cons | -4.827711 2.919208 -1.65 0.098 -10.54925 .8938321
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
cid: Identity |
sd(_cons) | 2.097709 .9227794 .8857332 4.96807
------------------------------------------------------------------------------
LR test vs. logistic regression: chibar2(01) = 11.44 Prob>=chibar2 = 0.0004
Say that we wanted to know the predicted probabilities for males and females at five different values of read, 30, 40, 50, 60 and 70. We might try using the margins command.
margins female, at(read=(30(10)70)) vsquish default prediction is a function of possibly stochastic quantities other than e(b) r(498);
That didn’t work because margins can’t compute predicted values for models that have both fixed and random components.
We can, however, get the predicted probabilities from just the fixed part of the model, like this.
margins female, at(read=(30(10)70)) predict(mu fixedonly) vsquish
Adjusted predictions Number of obs = 200
Expression : Predicted mean, fixed portion only, predict(mu fixedonly)
1._at : read = 30
2._at : read = 40
3._at : read = 50
4._at : read = 60
5._at : read = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at#female |
1 0 | .027962 .0353643 0.79 0.429 -.0413509 .0972748
1 1 | .0874748 .1006056 0.87 0.385 -.1097085 .2846582
2 0 | .0422023 .0352079 1.20 0.231 -.0268039 .1112085
2 1 | .1280315 .0900429 1.42 0.155 -.0484494 .3045123
3 0 | .0632231 .0416911 1.52 0.129 -.01849 .1449363
3 1 | .1836082 .0928378 1.98 0.048 .0016494 .365567
4 0 | .0936902 .0807071 1.16 0.246 -.0644929 .2518733
4 1 | .2562211 .1691374 1.51 0.130 -.075282 .5877243
5 0 | .1366968 .1661537 0.82 0.411 -.1889584 .462352
5 1 | .3454012 .3085949 1.12 0.263 -.2594336 .9502361
------------------------------------------------------------------------------
For many purposes these probabilities from the fixed effects only will be all that we will need and these probabilities could be graphed using marginsplot. If we are specifically interested in the estimated of probabilities that include both fixed and random effects we can make use of the predict command.
First, we will estimate the predicted probabilities from the fixed and random parts of the model directly.
predict mu1, mu
tabstat mu1, by(female)
Summary for variables: mu1
by categories of: female
female | mean
-------+----------
male | .1909927
female | .3182445
-------+----------
Total | .2603449
------------------
The values produced by tabstat give us the predicted probabilities separately for males and females while read is held at its observed values. We can estimate these same values in two steps by estimating the linear predictor for the random and fixed effects separately.
predict re*, reffects // linear predictor for the random effects
predict xb, xb // linear predictor for the fixed effects
gen mu2 = 1 /(1+exp(-1*(xb + re1))) // compute probabilities using both fixed and random components
tabstat mu2, by(female)
Summary for variables: mu2
by categories of: female
female | mean
-------+----------
male | .1909927
female | .3182445
-------+----------
Total | .2603449
------------------
As you can see the predicted probabilities computed this way are the same as when we predicted mu1 directly. The term (xb + re1) combines the fixed and random linear predictors while 1 /(1+exp(-1*(xb + re1))) converts the predictions to the probability metric.
We will now use the same approach to fix read at its mean value while letting female vary as observed.
sum read
replace read = r(mean)
predict xb3, xb
gen mu3 = 1 /(1+exp(-1*(xb3 + re1)))
tabstat mu3, by(female)
Summary for variables: mu3
by categories of: female
female | mean
-------+----------
male | .1588983
female | .3037404
-------+----------
Total | .2378372
------------------
We can use this same method to compute predicted probabilities for each gender at the five values of read of interest by computing a separate xb for each combination of values. We can continue to use the the linear random predictor, re1, because the observations remain nested in the same cid. We will do the computations in a forvalues loop.
forvalues i=30(10)70 {
quietly replace read = `i'
quietly replace female = 0 // begin with the males
predict xbm`i' , xb
gen mum`i' = 1 /(1+exp(-1*(xbm`i' + re1)))
quietly replace female = 1 // now for the females
predict xbf`i' , xb
gen muf`i' = 1 /(1+exp(-1*(xbf`i' + re1)))
}
sum mum* muf*
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
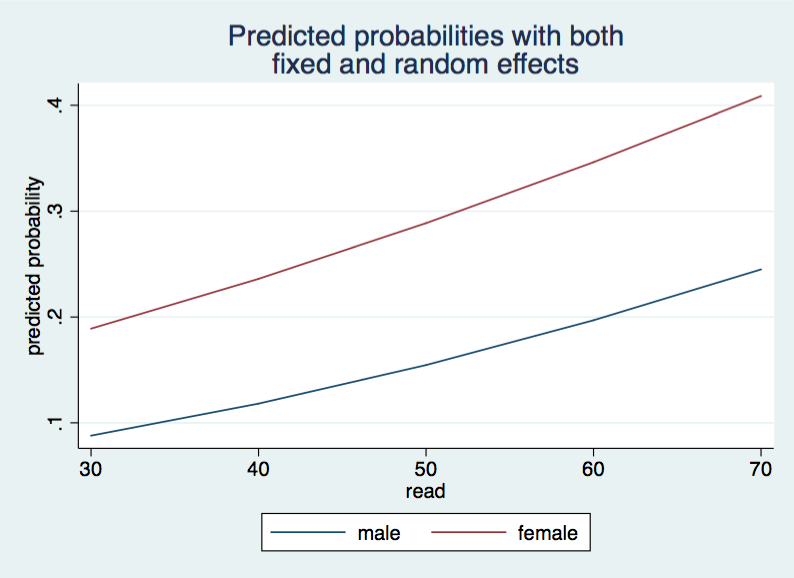
mum30 | 200 .0878644 .1277633 .0062536 .452949
mum40 | 200 .1181626 .161502 .0095469 .5591283
mum50 | 200 .1545762 .1959134 .0145493 .660161
mum60 | 200 .1969638 .2284821 .0221143 .7484569
mum70 | 200 .2450655 .2570279 .0334791 .8200648
-------------+--------------------------------------------------------
muf30 | 200 .189036 .2229538 .0205396 .7339823
muf40 | 200 .2361479 .2523496 .0311209 .8086573
muf50 | 200 .2887174 .2762624 .0468924 .8661915
muf60 | 200 .3463831 .2931488 .0700785 .9083859
muf70 | 200 .4087083 .3014779 .1034842 .9382238
The variables that begin mum give the predicted values for the males for each of the five different values of read. The muf do the same thing for the females. We will plot these values by collapsing the data to a single observation and then reshaping the data long.
collapse (mean) mum* muf*
gen tid = 1
reshape long mum muf, i(tid) j(read)
twoway (line mum read)(line muf read), legend(order(1 "male" 2 "female")) ///
ytitle(predicted probability) ///
title("Predicted probabilities with both" "fixed and random effects") ///
name(mu, replace)
With this approach you can replace the observed values with the mean values or any value that you wish. So, this approach worked okay for random intercepts, how would it work if we include a random coefficient (slope).
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
xtmelogit honors i.female read || cid: female, cov(unstr)
Refining starting values:
Iteration 0: log likelihood = -81.308446
Iteration 1: log likelihood = -79.509044
Iteration 2: log likelihood = -79.233888
Performing gradient-based optimization:
Iteration 0: log likelihood = -79.233888
Iteration 1: log likelihood = -79.203192
Iteration 2: log likelihood = -79.20305
Iteration 3: log likelihood = -79.20305
Mixed-effects logistic regression Number of obs = 200
Group variable: cid Number of groups = 20
Obs per group: min = 7
avg = 10.0
max = 12
Integration points = 7 Wald chi2(2) = 2.07
Log likelihood = -79.20305 Prob > chi2 = 0.3544
------------------------------------------------------------------------------
honors | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.female | 1.107571 .9144827 1.21 0.226 -.6847819 2.899924
read | .0548958 .0614466 0.89 0.372 -.0655374 .1753289
_cons | -5.459728 3.237309 -1.69 0.092 -11.80474 .8852801
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
cid: Unstructured |
sd(female) | 1.270624 .877583 .3281837 4.919457
sd(_cons) | 2.104286 1.168272 .7088079 6.247133
corr(female,_cons) | -.1370656 1.016493 -.9741795 .9555909
------------------------------------------------------------------------------
LR test vs. logistic regression: chi2(3) = 12.48 Prob > chi2 = 0.0059
Note: LR test is conservative and provided only for reference.
predict mu1, mu
tabstat mu1, by(female)
Summary for variables: mu1
by categories of: female
female | mean
-------+----------
male | .1884487
female | .3188527
-------+----------
Total | .2595188
------------------
To reproduce the predicted probabilities that include both fixed and random effects, we need to obtain the linear predictor of the random effects as follows:
predict re*, reffects // obtain the random effects
des re*
storage display value
variable name type format label variable label
--------------------------------------------------------------------------------------------
read byte %9.0g reading score
re1 float %9.0g random effects for cid: female
re2 float %9.0g random effects for cid: _cons
As you can see, re1 is the linear predictor for the random coefficient while re2 linear the linear predictor for the random intercept.
Now we need to compute the interaction of female with re1, obtain the linear predictor for the fixed effect and compute the probability.
gen fre1=female*re1
predict xb2, xb
gen mu2 = 1 /(1+exp(-1*(xb2 + fre1 + re2)))
tabstat mu2, by(female)
Summary for variables: mu2
by categories of: female
female | mean
-------+----------
male | .1884487
female | .3188527
-------+----------
Total | .2595188
------------------
Once again mu1 and mu2 are the same.
Next, with this knowledge, we are going to compute the predicted probabilities for read for the values 30, 40 50 60 and 70 for both males and females, just like we did in the first section. This time we need to compute fre1 for both males and female. For male the value of female*re1 is zero. While for female the value of female*re1 is equal to re1.
forvalues i=30(10)70 {
quietly replace read = `i'
quietly replace female = 0
quietly replace fre1 = 0 // this value is 0 for males
predict xbm`i' , xb
gen mum`i' = 1 /(1+exp(-1*(xbm`i' +fre1 + re2)))
quietly replace female = 1
quietly replace fre1 = re1 // this value is re1 for females
predict xbf`i' , xb
gen muf`i' = 1 /(1+exp(-1*(xbf`i' + fre1 + re2)))
}
sum mum* muf*
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
mum30 | 200 .067521 .1073255 .0062084 .4335063
mum40 | 200 .1006205 .1453719 .010701 .5698889
mum50 | 200 .1441323 .1850342 .0183843 .6964301
mum60 | 200 .1988144 .2226292 .031409 .7988807
mum70 | 200 .2647876 .2545738 .0531617 .8730579
-------------+--------------------------------------------------------
muf30 | 200 .1651364 .2082666 .0140494 .5906218
muf40 | 200 .2210162 .252848 .0240784 .7141231
muf50 | 200 .2841479 .2869894 .040969 .8122126
muf60 | 200 .3544923 .3071029 .0688718 .8821978
muf70 | 200 .432452 .3113492 .1135287 .9283999
As before we will collapse the data then reshape them prior to plotting.
collapse (mean) mum* muf*
gen tid = 1
reshape long mum muf, i(tid) j(read)
twoway (line mum read)(line muf read), legend(order(1 "male" 2 "female")) ///
ytitle(predicted probability) ///
title("Predicted probabilities with both" "fixed and random effects") ///
name(mu2, replace)
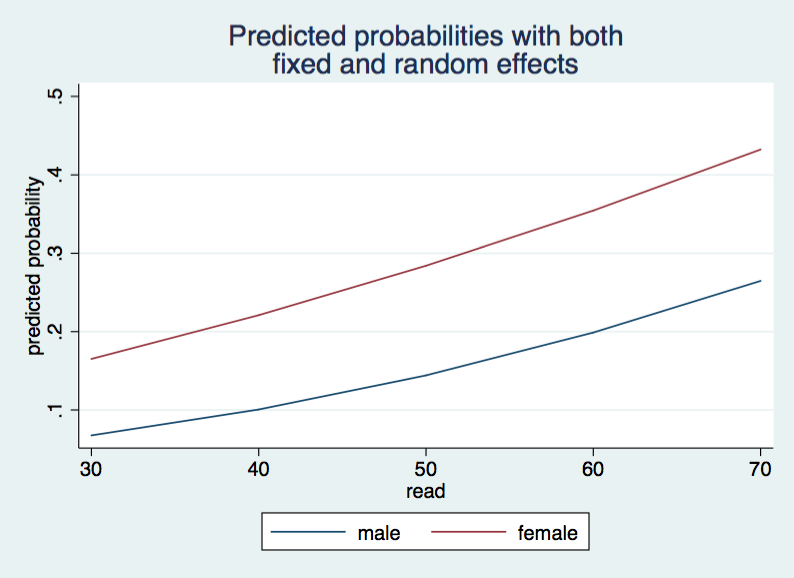
The two graphs that we generated for this page look very similar but inspection of the tables for the predicted probabilities show that adding the random coefficient to the model changes the predicted probabilities. Let’s check the two models using a likelihood-ratio test.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
quietly xtmelogit honors i.female read || cid: female, cov(unstr)
estimates store m1
quietly xtmelogit honors i.female read || cid:
estimates store m2
lrtest m1 m2
Likelihood-ratio test LR chi2(2) = 1.04
(Assumption: m1 nested in m2) Prob > chi2 = 0.5953
Note: The reported degrees of freedom assumes the null hypothesis is not on the boundary
of the parameter space. If this is not true, then the reported test is
conservative.
So, in this instance, the model with the random coefficient is not significantly better than the model with just the random intercept.
Acknowledgements: Thanks to Jurjen Iedema of the Netherlands Institute for Social Research / SCP for suggesting this approach.
