Stata has several procedures that can be used in analyzing count data. Let’s begin by loading and describing a dataset on 316 students at two Los Angeles high schools.
use https://stats.idre.ucla.edu/stat/stata/notes/lahigh, clear describe Contains data from lahigh.dta obs: 316 vars: 10 3 Dec 1999 09:43 size: 13,904 (98.5% of memory free) (_dta has notes) ------------------------------------------------------------------------------- 1. id float %9.0g 2. gender float %9.0g gl 3. ethnic float %10.0g el ethnicity 4. school float %9.0g school 1 or 2 5. mathpr float %9.0g ctbs math pct rank 6. langpr float %9.0g ctbs lang pct rank 7. mathnce float %9.0g ctbs math nce 8. langnce float %9.0g ctbs lang nce 9. biling float %12.0g bl bilingual status 10. daysabs float %9.0g number days absent ------------------------------------------------------------------------------- Sorted by:
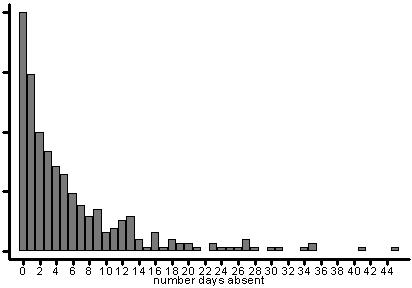
Let’s analyze the variable daysabs to see if there is an effect due to gender and ability as measured by mathnce and langnce. To begin with, we have always been warned against using count data in OLS regression. A simple histogram can show us that this is a good recommendation.
hist daysabs
The data are strongly skewed to the right, so clearly OLS regression would be inappropriate. Count data often follow a poisson distribution, so some type of poisson analysis might be appropriate. Recall from statistical theory that in a poisson distribution the mean and variance are the same. Let’s summarize daysabs using the detail option.
summarize daysabs, detail
number days absent
-------------------------------------------------------------
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 316
25% 1 0 Sum of Wgt. 316
50% 3 Mean 5.810127
Largest Std. Dev. 7.449003
75% 8 35
90% 14 35 Variance 55.48764
95% 23 41 Skewness 2.250587
99% 35 45 Kurtosis 8.949302
The variance of daysabs is nearly 10 times larger than the mean. The distribution of daysabs is displaying signs of overdispersion, that is, greater variance than might be expected in a poisson distribution. Before we get to an alternative analysis, let’s run a poisson regression, even though we believe that the poisson distribution is not correct. Poisson regression can be followed up with the poisgof command which tests the poisson goodness-of-fit. Here is what these commands look like.
poisson daysabs gender mathnce langnce
Iteration 0: log likelihood = -1547.9709
Iteration 1: log likelihood = -1547.9709
Poisson regression Number of obs = 316
LR chi2(3) = 175.27
Prob > chi2 = 0.0000
Log likelihood = -1547.9709 Pseudo R2 = 0.0536
------------------------------------------------------------------------------
daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
gender | -.4009209 .0484122 -8.281 0.000 -.495807 -.3060348
mathnce | -.0035232 .0018213 -1.934 0.053 -.007093 .0000466
langnce | -.0121521 .0018348 -6.623 0.000 -.0157483 -.0085559
_cons | 3.088587 .1017365 30.359 0.000 2.889187 3.287987
------------------------------------------------------------------------------
* Stata 8 code.
poisgof
* Stata 9 and 10 code and output.
estat gof
Goodness of fit chi-2 = 2234.546
Prob > chi2(312) = 0.0000
The large value for chi-square in the gof is another indicator that the poisson distribution is not a good choice. A significant (p<0.05) test statistic from the gof indicates that the poisson model is inapproprite. Let’s run the analysis one more time, this time using negative binomial regression. Negative binomial regression is often more appropriate in cases of overdispersion. Here is the negative binomial analysis.
nbreg daysabs gender mathnce langnce
Fitting comparison Poisson model:
Iteration 0: log likelihood = -1547.9709
Iteration 1: log likelihood = -1547.9709
Fitting constant-only model:
Iteration 0: log likelihood = -897.78991
Iteration 1: log likelihood = -891.24455
Iteration 2: log likelihood = -891.24271
Iteration 3: log likelihood = -891.24271
Fitting full model:
Iteration 0: log likelihood = -881.57337
Iteration 1: log likelihood = -880.87788
Iteration 2: log likelihood = -880.87312
Iteration 3: log likelihood = -880.87312
Negative binomial regression Number of obs = 316
LR chi2(3) = 20.74
Prob > chi2 = 0.0001
Log likelihood = -880.87312 Pseudo R2 = 0.0116
------------------------------------------------------------------------------
daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
gender | -.4311844 .1396656 -3.087 0.002 -.704924 -.1574448
mathnce | -.001601 .00485 -0.330 0.741 -.0111067 .0079048
langnce | -.0143475 .0055815 -2.571 0.010 -.0252871 -.003408
_cons | 3.147254 .3211669 9.799 0.000 2.517778 3.776729
---------+--------------------------------------------------------------------
/lnalpha | .2533877 .0955362 .0661402 .4406351
---------+--------------------------------------------------------------------
alpha | 1.288383 .1230871 10.467 0.000 1.068377 1.553694
------------------------------------------------------------------------------
Likelihood ratio test of alpha=0: chi2(1) = 1334.20 Prob > chi2 = 0.0000
The likelihood ratio test at the bottom of the analysis is a test of the overdispersion parameter alpha. When the overdispersion parameter is zero the negative binomial distrbution is equivalent to a poisson distribution. In this case, alpha is significantly different from zero and thus reinforces one last time that the poisson distribution is not appropriate.
In the analysis itself, both gender and langnce are significant while mathnce is not. From the coding of gender (1=female, 2=male) it is evident that females are absent significantly more than are males. The significant coefficient for langnce suggests that higher ability students are absent less often than lower ability students.