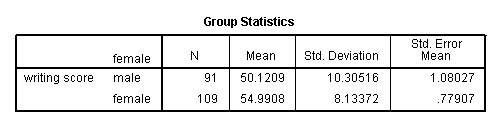Introduction
This page shows how to perform a number of statistical tests using SPSS. Each section gives a brief description of the aim of the statistical test, when it is used, an example showing the SPSS commands and SPSS (often abbreviated) output with a brief interpretation of the output. You can see the page Choosing the Correct Statistical Test for a table that shows an overview of when each test is appropriate to use. In deciding which test is appropriate to use, it is important to consider the type of variables that you have (i.e., whether your variables are categorical, ordinal or interval and whether they are normally distributed), see What is the difference between categorical, ordinal and interval variables? for more information on this.
About the hsb data file
Most of the examples in this page will use a data file called hsb2, high school and beyond. This data file contains 200 observations from a sample of high school students with demographic information about the students, such as their gender (female), socio-economic status (ses) and ethnic background (race). It also contains a number of scores on standardized tests, including tests of reading (read), writing (write), mathematics (math) and social studies (socst). You can get the hsb data file by clicking on hsb2.
One sample t-test
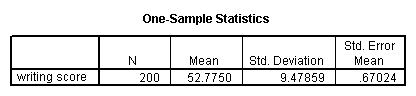
A one sample t-test allows us to test whether a sample mean (of a normally distributed interval variable) significantly differs from a hypothesized value. For example, using the hsb2 data file, say we wish to test whether the average writing score (write) differs significantly from 50. We can do this as shown below.
t-test /testval = 50 /variable = write.
The mean of the variable write for this particular sample of students is 52.775, which is statistically significantly different from the test value of 50. We would conclude that this group of students has a significantly higher mean on the writing test than 50.
One sample median test
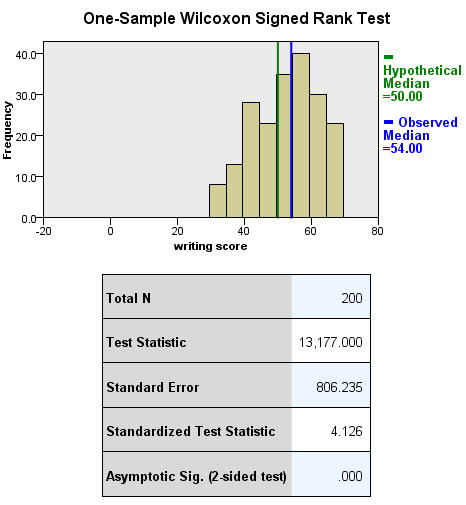
A one sample median test allows us to test whether a sample median differs significantly from a hypothesized value. We will use the same variable, write, as we did in the one sample t-test example above, but we do not need to assume that it is interval and normally distributed (we only need to assume that write is an ordinal variable).
nptests /onesample test (write) wilcoxon(testvalue = 50).

Binomial test
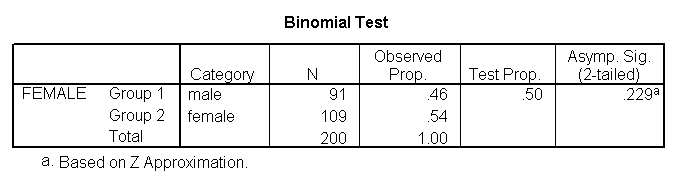
A one sample binomial test allows us to test whether the proportion of successes on a two-level categorical dependent variable significantly differs from a hypothesized value. For example, using the hsb2 data file, say we wish to test whether the proportion of females (female) differs significantly from 50%, i.e., from .5. We can do this as shown below.
npar tests /binomial (.5) = female.
The results indicate that there is no statistically significant difference (p = .229). In other words, the proportion of females in this sample does not significantly differ from the hypothesized value of 50%.
Chi-square goodness of fit
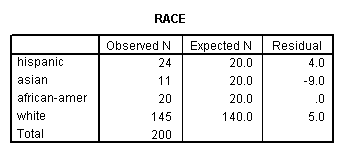
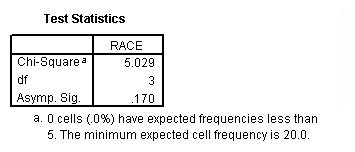
A chi-square goodness of fit test allows us to test whether the observed proportions for a categorical variable differ from hypothesized proportions. For example, let’s suppose that we believe that the general population consists of 10% Hispanic, 10% Asian, 10% African American and 70% White folks. We want to test whether the observed proportions from our sample differ significantly from these hypothesized proportions.
npar test /chisquare = race /expected = 10 10 10 70.
These results show that racial composition in our sample does not differ significantly from the hypothesized values that we supplied (chi-square with three degrees of freedom = 5.029, p = .170).
Two independent samples t-test
An independent samples t-test is used when you want to compare the means of a normally distributed interval dependent variable for two independent groups. For example, using the hsb2 data file, say we wish to test whether the mean for write is the same for males and females.
t-test groups = female(0 1) /variables = write.
Because the standard deviations for the two groups are similar (10.3 and 8.1), we will use the “equal variances assumed” test. The results indicate that there is a statistically significant difference between the mean writing score for males and females (t = -3.734, p = .000). In other words, females have a statistically significantly higher mean score on writing (54.99) than males (50.12).
See also
Wilcoxon-Mann-Whitney test
The Wilcoxon-Mann-Whitney test is a non-parametric analog to the independent samples t-test and can be used when you do not assume that the dependent variable is a normally distributed interval variable (you only assume that the variable is at least ordinal). You will notice that the SPSS syntax for the Wilcoxon-Mann-Whitney test is almost identical to that of the independent samples t-test. We will use the same data file (the hsb2 data file) and the same variables in this example as we did in the independent t-test example above and will not assume that write, our dependent variable, is normally distributed.
npar test /m-w = write by female(0 1).The results suggest that there is a statistically significant difference between the underlying distributions of the write scores of males and the write scores of females (z = -3.329, p = 0.001).
See also
Chi-square test
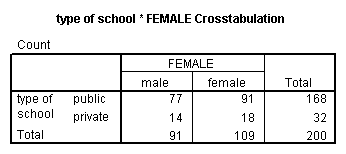
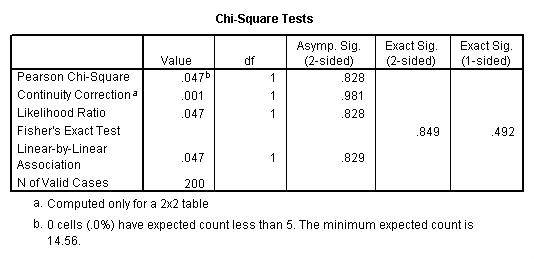
A chi-square test is used when you want to see if there is a relationship between two categorical variables. In SPSS, the chisq option is used on the statistics subcommand of the crosstabs command to obtain the test statistic and its associated p-value. Using the hsb2 data file, let’s see if there is a relationship between the type of school attended (schtyp) and students’ gender (female). Remember that the chi-square test assumes that the expected value for each cell is five or higher. This assumption is easily met in the examples below. However, if this assumption is not met in your data, please see the section on Fisher’s exact test below.
crosstabs /tables = schtyp by female /statistic = chisq.
These results indicate that there is no statistically significant relationship between the type of school attended and gender (chi-square with one degree of freedom = 0.047, p = 0.828).
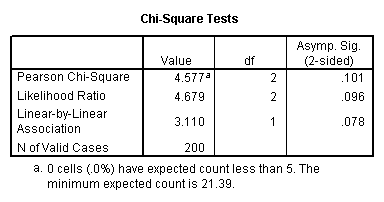
Let’s look at another example, this time looking at the linear relationship between gender (female) and socio-economic status (ses). The point of this example is that one (or both) variables may have more than two levels, and that the variables do not have to have the same number of levels. In this example, female has two levels (male and female) and ses has three levels (low, medium and high).
crosstabs /tables = female by ses /statistic = chisq.
Again we find that there is no statistically significant relationship between the variables (chi-square with two degrees of freedom = 4.577, p = 0.101).
See also
Fisher’s exact test
The Fisher’s exact test is used when you want to conduct a chi-square test but one or more of your cells has an expected frequency of five or less. Remember that the chi-square test assumes that each cell has an expected frequency of five or more, but the Fisher’s exact test has no such assumption and can be used regardless of how small the expected frequency is. In SPSS unless you have the SPSS Exact Test Module, you can only perform a Fisher’s exact test on a 2×2 table, and these results are presented by default. Please see the results from the chi squared example above.
One-way ANOVA
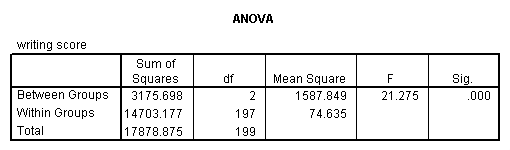
A one-way analysis of variance (ANOVA) is used when you have a categorical independent variable (with two or more categories) and a normally distributed interval dependent variable and you wish to test for differences in the means of the dependent variable broken down by the levels of the independent variable. For example, using the hsb2 data file, say we wish to test whether the mean of write differs between the three program types (prog). The command for this test would be:
oneway write by prog.
The mean of the dependent variable differs significantly among the levels of program type. However, we do not know if the difference is between only two of the levels or all three of the levels. (The F test for the Model is the same as the F test for prog because prog was the only variable entered into the model. If other variables had also been entered, the F test for the Model would have been different from prog.) To see the mean of write for each level of program type,
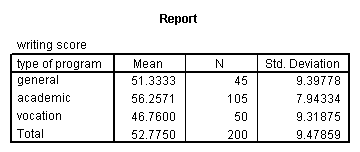
means tables = write by prog.
From this we can see that the students in the academic program have the highest mean writing score, while students in the vocational program have the lowest.
See also
Kruskal Wallis test
The Kruskal Wallis test is used when you have one independent variable with two or more levels and an ordinal dependent variable. In other words, it is the non-parametric version of ANOVA and a generalized form of the Mann-Whitney test method since it permits two or more groups. We will use the same data file as the one way ANOVA example above (the hsb2 data file) and the same variables as in the example above, but we will not assume that write is a normally distributed interval variable.
npar tests /k-w = write by prog (1,3).
If some of the scores receive tied ranks, then a correction factor is used, yielding a slightly different value of chi-squared. With or without ties, the results indicate that there is a statistically significant difference among the three type of programs.
Paired t-test
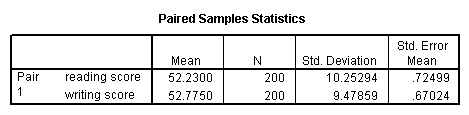
A paired (samples) t-test is used when you have two related observations (i.e., two observations per subject) and you want to see if the means on these two normally distributed interval variables differ from one another. For example, using the hsb2 data file we will test whether the mean of read is equal to the mean of write.
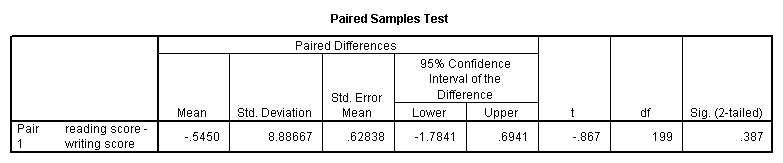
t-test pairs = read with write (paired).
These results indicate that the mean of read is not statistically significantly different from the mean of write (t = -0.867, p = 0.387).
Wilcoxon signed rank sum test
The Wilcoxon signed rank sum test is the non-parametric version of a paired samples t-test. You use the Wilcoxon signed rank sum test when you do not wish to assume that the difference between the two variables is interval and normally distributed (but you do assume the difference is ordinal). We will use the same example as above, but we will not assume that the difference between read and write is interval and normally distributed.
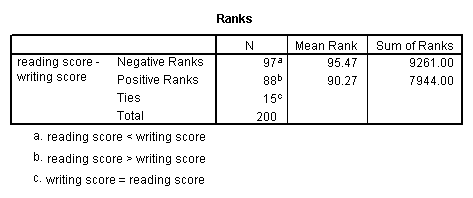
npar test /wilcoxon = write with read (paired).
The results suggest that there is not a statistically significant difference between read and write.
If you believe the differences between read and write were not ordinal but could merely be classified as positive and negative, then you may want to consider a sign test in lieu of sign rank test. Again, we will use the same variables in this example and assume that this difference is not ordinal.
npar test /sign = read with write (paired).
We conclude that no statistically significant difference was found (p=.556).
McNemar test
You would perform McNemar’s test if you were interested in the marginal frequencies of two binary outcomes. These binary outcomes may be the same outcome variable on matched pairs (like a case-control study) or two outcome variables from a single group. Continuing with the hsb2 dataset used in several above examples, let us create two binary outcomes in our dataset: himath and hiread. These outcomes can be considered in a two-way contingency table. The null hypothesis is that the proportion of students in the himath group is the same as the proportion of students in hiread group (i.e., that the contingency table is symmetric).
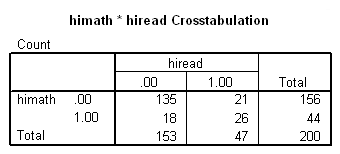
compute himath = (math>60). compute hiread = (read>60). execute. crosstabs /tables=himath BY hiread /statistic=mcnemar /cells=count.
McNemar’s chi-square statistic suggests that there is not a statistically significant difference in the proportion of students in the himath group and the proportion of students in the hiread group.
One-way repeated measures ANOVA
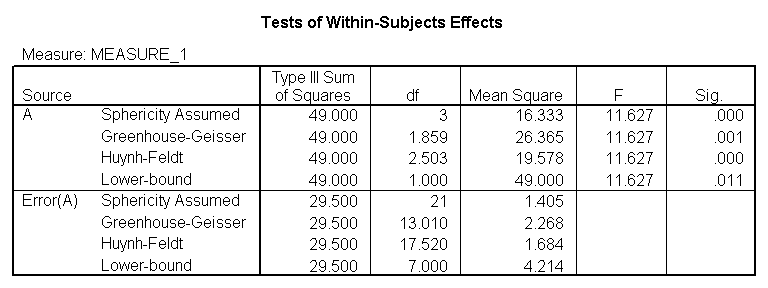
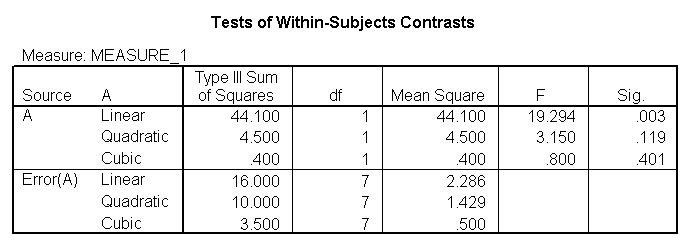
You would perform a one-way repeated measures analysis of variance if you had one categorical independent variable and a normally distributed interval dependent variable that was repeated at least twice for each subject. This is the equivalent of the paired samples t-test, but allows for two or more levels of the categorical variable. This tests whether the mean of the dependent variable differs by the categorical variable. We have an example data set called rb4wide, which is used in Kirk’s book Experimental Design. In this data set, y is the dependent variable, a is the repeated measure and s is the variable that indicates the subject number.
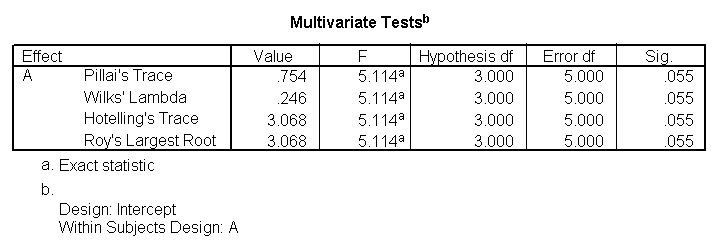
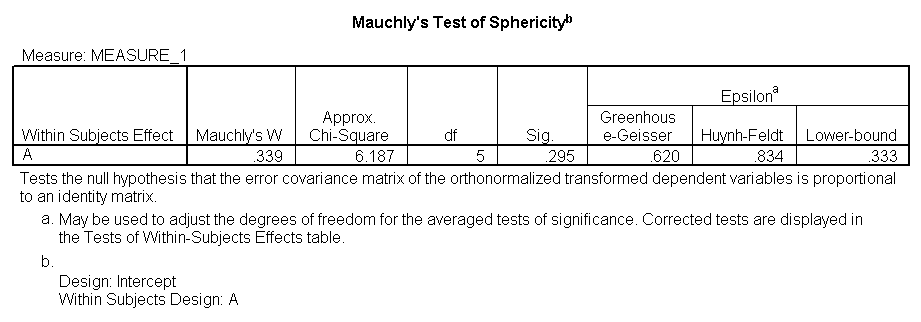
glm y1 y2 y3 y4 /wsfactor a(4).
You will notice that this output gives four different p-values. The output labeled “sphericity assumed” is the p-value (0.000) that you would get if you assumed compound symmetry in the variance-covariance matrix. Because that assumption is often not valid, the three other p-values offer various corrections (the Huynh-Feldt, H-F, Greenhouse-Geisser, G-G and Lower-bound). No matter which p-value you use, our results indicate that we have a statistically significant effect of a at the .05 level.
See also
Repeated measures logistic regression
If you have a binary outcome measured repeatedly for each subject and you wish to run a logistic regression that accounts for the effect of multiple measures from single subjects, you can perform a repeated measures logistic regression. In SPSS, this can be done using the GENLIN command and indicating binomial as the probability distribution and logit as the link function to be used in the model. The exercise data file contains 3 pulse measurements from each of 30 people assigned to 2 different diet regiments and 3 different exercise regiments. If we define a “high” pulse as being over 100, we can then predict the probability of a high pulse using diet regiment.
GET FILE='C:mydatahttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/exercise.sav'.GENLIN highpulse (REFERENCE=LAST) BY diet (order = DESCENDING) /MODEL diet DISTRIBUTION=BINOMIAL LINK=LOGIT /REPEATED SUBJECT=id CORRTYPE = EXCHANGEABLE.
These results indicate that diet is not statistically significant (Wald Chi-Square = 1.562, p = 0.211).
Factorial ANOVA
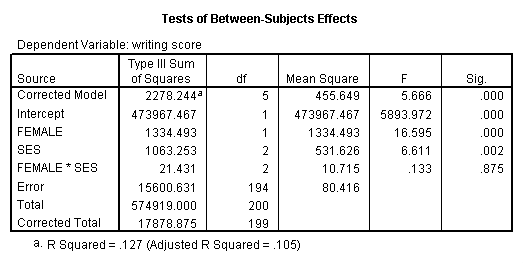
A factorial ANOVA has two or more categorical independent variables (either with or without the interactions) and a single normally distributed interval dependent variable. For example, using the hsb2 data file we will look at writing scores (write) as the dependent variable and gender (female) and socio-economic status (ses) as independent variables, and we will include an interaction of female by ses. Note that in SPSS, you do not need to have the interaction term(s) in your data set. Rather, you can have SPSS create it/them temporarily by placing an asterisk between the variables that will make up the interaction term(s).
glm write by female ses.These results indicate that the overall model is statistically significant (F = 5.666, p = 0.00). The variables female and ses are also statistically significant (F = 16.595, p = 0.000 and F = 6.611, p = 0.002, respectively). However, that interaction between female and ses is not statistically significant (F = 0.133, p = 0.875).
See also
Friedman test
You perform a Friedman test when you have one within-subjects independent variable with two or more levels and a dependent variable that is not interval and normally distributed (but at least ordinal). We will use this test to determine if there is a difference in the reading, writing and math scores. The null hypothesis in this test is that the distribution of the ranks of each type of score (i.e., reading, writing and math) are the same. To conduct a Friedman test, the data need to be in a long format. SPSS handles this for you, but in other statistical packages you will have to reshape the data before you can conduct this test.
npar tests /friedman = read write math.
Friedman’s chi-square has a value of 0.645 and a p-value of 0.724 and is not statistically significant. Hence, there is no evidence that the distributions of the three types of scores are different.
Ordered logistic regression
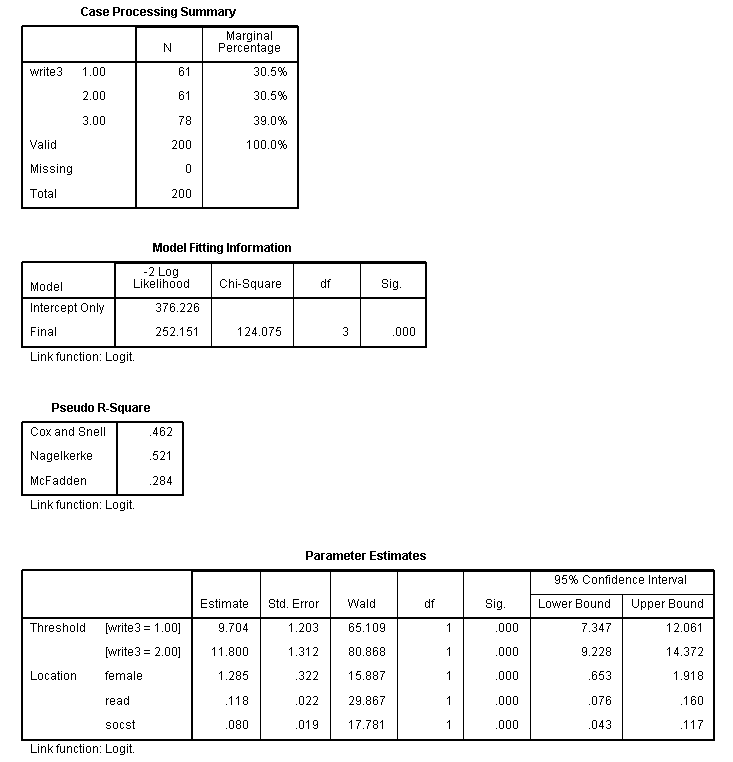
Ordered logistic regression is used when the dependent variable is ordered, but not continuous. For example, using the hsb2 data file we will create an ordered variable called write3. This variable will have the values 1, 2 and 3, indicating a low, medium or high writing score. We do not generally recommend categorizing a continuous variable in this way; we are simply creating a variable to use for this example. We will use gender (female), reading score (read) and social studies score (socst) as predictor variables in this model. We will use a logit link and on the print subcommand we have requested the parameter estimates, the (model) summary statistics and the test of the parallel lines assumption.
if write ge 30 and write le 48 write3 = 1. if write ge 49 and write le 57 write3 = 2. if write ge 58 and write le 70 write3 = 3. execute. plum write3 with female read socst /link = logit /print = parameter summary tparallel.
The results indicate that the overall model is statistically significant (p < .000), as are each of the predictor variables (p < .000). There are two thresholds for this model because there are three levels of the outcome variable. We also see that the test of the proportional odds assumption is non-significant (p = .563). One of the assumptions underlying ordinal logistic (and ordinal probit) regression is that the relationship between each pair of outcome groups is the same. In other words, ordinal logistic regression assumes that the coefficients that describe the relationship between, say, the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories, etc. This is called the proportional odds assumption or the parallel regression assumption. Because the relationship between all pairs of groups is the same, there is only one set of coefficients (only one model). If this was not the case, we would need different models (such as a generalized ordered logit model) to describe the relationship between each pair of outcome groups.
See also
Factorial logistic regression
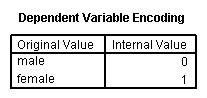
A factorial logistic regression is used when you have two or more categorical independent variables but a dichotomous dependent variable. For example, using the hsb2 data file we will use female as our dependent variable, because it is the only dichotomous variable in our data set; certainly not because it common practice to use gender as an outcome variable. We will use type of program (prog) and school type (schtyp) as our predictor variables. Because prog is a categorical variable (it has three levels), we need to create dummy codes for it. SPSS will do this for you by making dummy codes for all variables listed after the keyword with. SPSS will also create the interaction term; simply list the two variables that will make up the interaction separated by the keyword by.
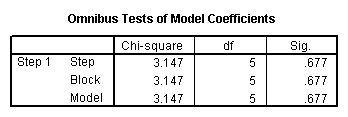
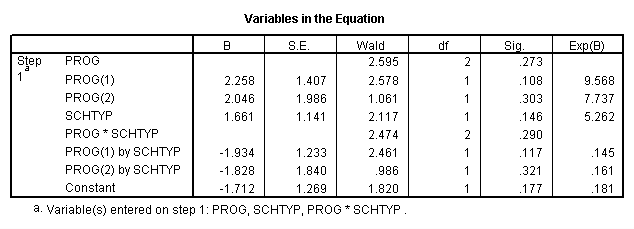
logistic regression female with prog schtyp prog by schtyp /contrast(prog) = indicator(1).
The results indicate that the overall model is not statistically significant (LR chi2 = 3.147, p = 0.677). Furthermore, none of the coefficients are statistically significant either. This shows that the overall effect of prog is not significant.
See also
Correlation
A correlation is useful when you want to see the relationship between two (or more) normally distributed interval variables. For example, using the hsb2 data file we can run a correlation between two continuous variables, read and write.
correlations /variables = read write.In the second example, we will run a correlation between a dichotomous variable, female, and a continuous variable, write. Although it is assumed that the variables are interval and normally distributed, we can include dummy variables when performing correlations.
correlations /variables = female write.In the first example above, we see that the correlation between read and write is 0.597. By squaring the correlation and then multiplying by 100, you can determine what percentage of the variability is shared. Let’s round 0.597 to be 0.6, which when squared would be .36, multiplied by 100 would be 36%. Hence read shares about 36% of its variability with write. In the output for the second example, we can see the correlation between write and female is 0.256. Squaring this number yields .065536, meaning that female shares approximately 6.5% of its variability with write.
See also
Simple linear regression
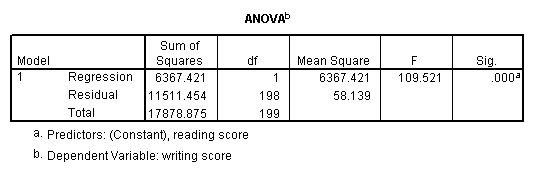
Simple linear regression allows us to look at the linear relationship between one normally distributed interval predictor and one normally distributed interval outcome variable. For example, using the hsb2 data file, say we wish to look at the relationship between writing scores (write) and reading scores (read); in other words, predicting write from read.
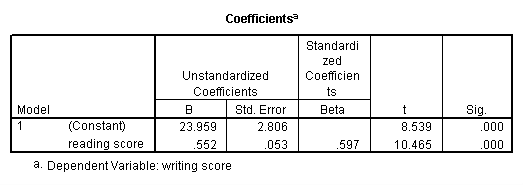
regression variables = write read /dependent = write /method = enter.
We see that the relationship between write and read is positive (.552) and based on the t-value (10.47) and p-value (0.000), we would conclude this relationship is statistically significant. Hence, we would say there is a statistically significant positive linear relationship between reading and writing.
See also
Non-parametric correlation
A Spearman correlation is used when one or both of the variables are not assumed to be normally distributed and interval (but are assumed to be ordinal). The values of the variables are converted in ranks and then correlated. In our example, we will look for a relationship between read and write. We will not assume that both of these variables are normal and interval.
nonpar corr /variables = read write /print = spearman.The results suggest that the relationship between read and write (rho = 0.617, p = 0.000) is statistically significant.
Simple logistic regression
Logistic regression assumes that the outcome variable is binary (i.e., coded as 0 and 1). We have only one variable in the hsb2 data file that is coded 0 and 1, and that is female. We understand that female is a silly outcome variable (it would make more sense to use it as a predictor variable), but we can use female as the outcome variable to illustrate how the code for this command is structured and how to interpret the output. The first variable listed after the logistic command is the outcome (or dependent) variable, and all of the rest of the variables are predictor (or independent) variables. In our example, female will be the outcome variable, and read will be the predictor variable. As with OLS regression, the predictor variables must be either dichotomous or continuous; they cannot be categorical.
logistic regression female with read.
The results indicate that reading score (read) is not a statistically significant predictor of gender (i.e., being female), Wald = .562, p = 0.453. Likewise, the test of the overall model is not statistically significant, LR chi-squared – 0.56, p = 0.453.
See also
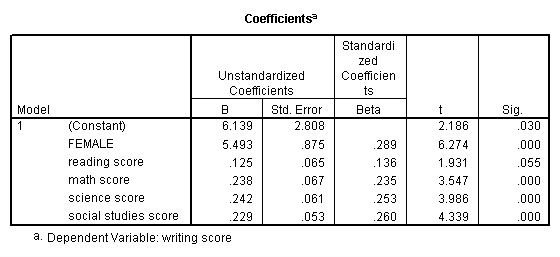
Multiple regression
Multiple regression is very similar to simple regression, except that in multiple regression you have more than one predictor variable in the equation. For example, using the hsb2 data file we will predict writing score from gender (female), reading, math, science and social studies (socst) scores.
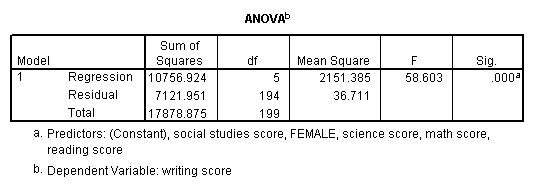
regression variable = write female read math science socst /dependent = write /method = enter.
The results indicate that the overall model is statistically significant (F = 58.60, p = 0.000). Furthermore, all of the predictor variables are statistically significant except for read.
See also
Analysis of covariance
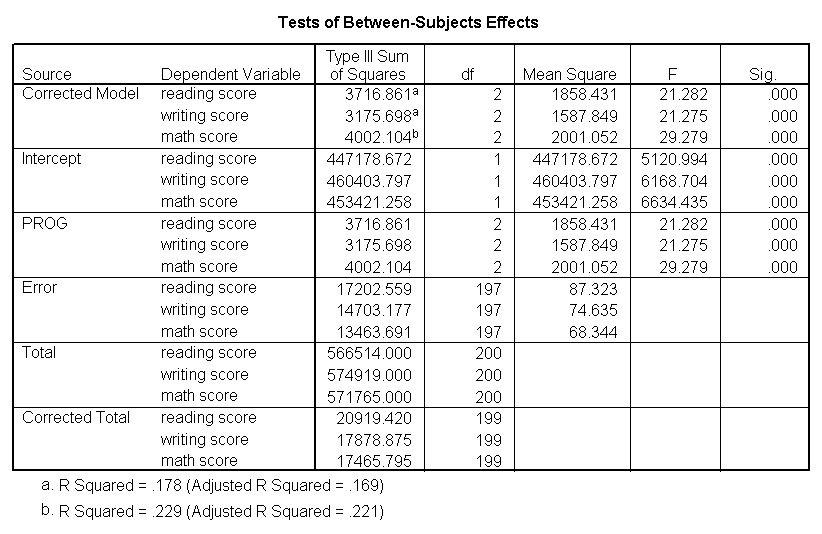
Analysis of covariance is like ANOVA, except in addition to the categorical predictors you also have continuous predictors as well. For example, the one way ANOVA example used write as the dependent variable and prog as the independent variable. Let’s add read as a continuous variable to this model, as shown below.
glm write with read by prog.
The results indicate that even after adjusting for reading score (read), writing scores still significantly differ by program type (prog), F = 5.867, p = 0.003.
See also
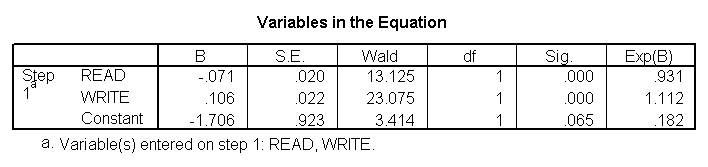
Multiple logistic regression
Multiple logistic regression is like simple logistic regression, except that there are two or more predictors. The predictors can be interval variables or dummy variables, but cannot be categorical variables. If you have categorical predictors, they should be coded into one or more dummy variables. We have only one variable in our data set that is coded 0 and 1, and that is female. We understand that female is a silly outcome variable (it would make more sense to use it as a predictor variable), but we can use female as the outcome variable to illustrate how the code for this command is structured and how to interpret the output. The first variable listed after the logistic regression command is the outcome (or dependent) variable, and all of the rest of the variables are predictor (or independent) variables (listed after the keyword with). In our example, female will be the outcome variable, and read and write will be the predictor variables.
logistic regression female with read write.
These results show that both read and write are significant predictors of female.
See also
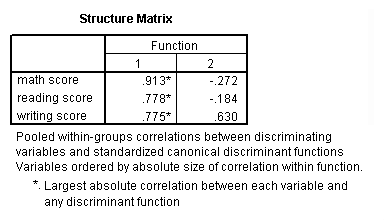
Discriminant analysis
Discriminant analysis is used when you have one or more normally distributed interval independent variables and a categorical dependent variable. It is a multivariate technique that considers the latent dimensions in the independent variables for predicting group membership in the categorical dependent variable. For example, using the hsb2 data file, say we wish to use read, write and math scores to predict the type of program a student belongs to (prog).
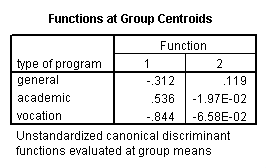
discriminate groups = prog(1, 3) /variables = read write math.
Clearly, the SPSS output for this procedure is quite lengthy, and it is beyond the scope of this page to explain all of it. However, the main point is that two canonical variables are identified by the analysis, the first of which seems to be more related to program type than the second.
See also
One-way MANOVA
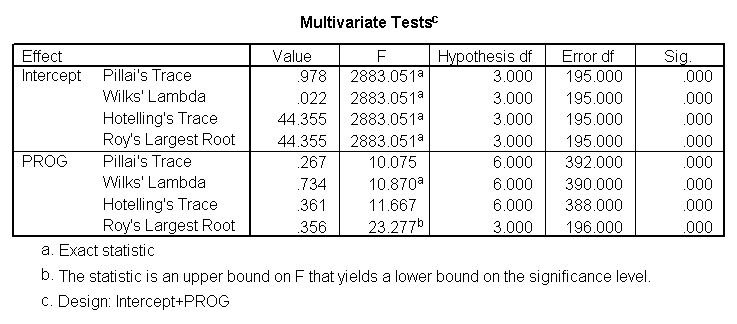
MANOVA (multivariate analysis of variance) is like ANOVA, except that there are two or more dependent variables. In a one-way MANOVA, there is one categorical independent variable and two or more dependent variables. For example, using the hsb2 data file, say we wish to examine the differences in read, write and math broken down by program type (prog).
glm read write math by prog.
The students in the different programs differ in their joint distribution of read, write and math.
See also
Multivariate multiple regression
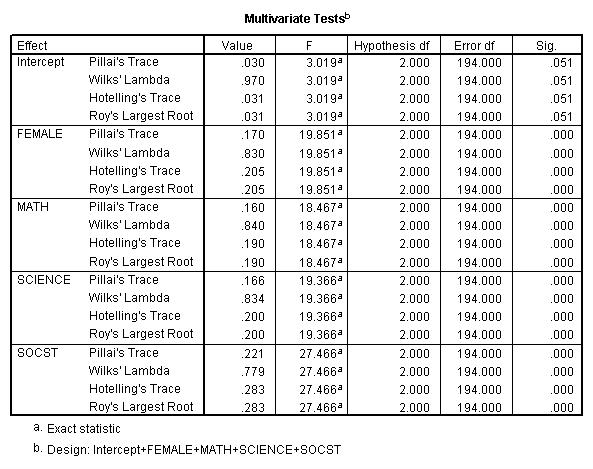
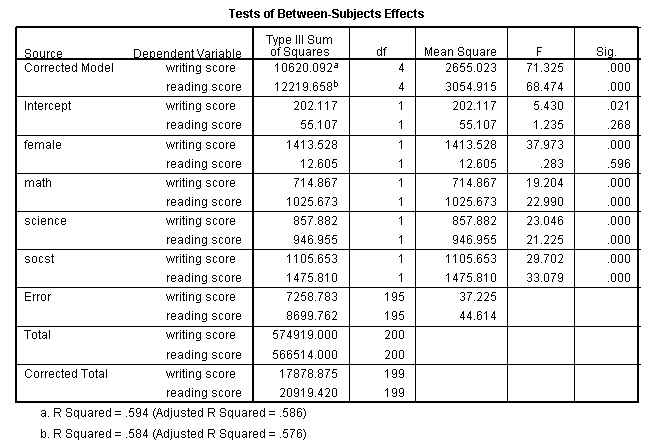
Multivariate multiple regression is used when you have two or more dependent variables that are to be predicted from two or more independent variables. In our example using the hsb2 data file, we will predict write and read from female, math, science and social studies (socst) scores.
glm write read with female math science socst.
These results show that all of the variables in the model have a statistically significant relationship with the joint distribution of write and read.
Canonical correlation
Canonical correlation is a multivariate technique used to examine the relationship between two groups of variables. For each set of variables, it creates latent variables and looks at the relationships among the latent variables. It assumes that all variables in the model are interval and normally distributed. SPSS requires that each of the two groups of variables be separated by the keyword with. There need not be an equal number of variables in the two groups (before and after the with).
manova read write with math science /discrim. * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. WITHIN CELLS Regression Multivariate Tests of Significance (S = 2, M = -1/2, N = 97 ) Test Name Value Approx. F Hypoth. DF Error DF Sig. of F Pillais .59783 41.99694 4.00 394.00 .000 Hotellings 1.48369 72.32964 4.00 390.00 .000 Wilks .40249 56.47060 4.00 392.00 .000 Roys .59728 Note.. F statistic for WILKS' Lambda is exact. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. WITHIN CELLS Regression (Cont.) Univariate F-tests with (2,197) D. F. Variable Sq. Mul. R Adj. R-sq. Hypoth. MS Error MS F READ .51356 .50862 5371.66966 51.65523 103.99081 WRITE .43565 .42992 3894.42594 51.21839 76.03569 Variable Sig. of F READ .000 WRITE .000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Raw canonical coefficients for DEPENDENT variables Function No. Variable 1 READ .063 WRITE .049 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Standardized canonical coefficients for DEPENDENT variables Function No. Variable 1 READ .649 WRITE .467 * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Correlations between DEPENDENT and canonical variables Function No. Variable 1 READ .927 WRITE .854 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Variance in dependent variables explained by canonical variables CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO 1 79.441 79.441 47.449 47.449 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Raw canonical coefficients for COVARIATES Function No. COVARIATE 1 MATH .067 SCIENCE .048 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Standardized canonical coefficients for COVARIATES CAN. VAR. COVARIATE 1 MATH .628 SCIENCE .478 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Correlations between COVARIATES and canonical variables CAN. VAR. Covariate 1 MATH .929 SCIENCE .873 * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Variance in covariates explained by canonical variables CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO 1 48.544 48.544 81.275 81.275 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Regression analysis for WITHIN CELLS error term --- Individual Univariate .9500 confidence intervals Dependent variable .. READ reading score COVARIATE B Beta Std. Err. t-Value Sig. of t MATH .48129 .43977 .070 6.868 .000 SCIENCE .36532 .35278 .066 5.509 .000 COVARIATE Lower -95% CL- Upper MATH .343 .619 SCIENCE .235 .496 Dependent variable .. WRITE writing score COVARIATE B Beta Std. Err. t-Value Sig. of t MATH .43290 .42787 .070 6.203 .000 SCIENCE .28775 .30057 .066 4.358 .000 COVARIATE Lower -95% CL- Upper MATH .295 .571 SCIENCE .158 .418 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. CONSTANT Multivariate Tests of Significance (S = 1, M = 0, N = 97 ) Test Name Value Exact F Hypoth. DF Error DF Sig. of F Pillais .11544 12.78959 2.00 196.00 .000 Hotellings .13051 12.78959 2.00 196.00 .000 Wilks .88456 12.78959 2.00 196.00 .000 Roys .11544 Note.. F statistics are exact. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. CONSTANT (Cont.) Univariate F-tests with (1,197) D. F. Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F READ 336.96220 10176.0807 336.96220 51.65523 6.52329 .011 WRITE 1209.88188 10090.0231 1209.88188 51.21839 23.62202 .000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. CONSTANT (Cont.) Raw discriminant function coefficients Function No. Variable 1 READ .041 WRITE .124 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Standardized discriminant function coefficients Function No. Variable 1 READ .293 WRITE .889 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Estimates of effects for canonical variables Canonical Variable Parameter 1 1 2.196 * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. CONSTANT (Cont.) Correlations between DEPENDENT and canonical variables Canonical Variable Variable 1 READ .504 WRITE .959 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -The output above shows the linear combinations corresponding to the first canonical correlation. At the bottom of the output are the two canonical correlations. These results indicate that the first canonical correlation is .7728. The F-test in this output tests the hypothesis that the first canonical correlation is equal to zero. Clearly, F = 56.4706 is statistically significant. However, the second canonical correlation of .0235 is not statistically significantly different from zero (F = 0.1087, p = 0.7420).
Factor analysis
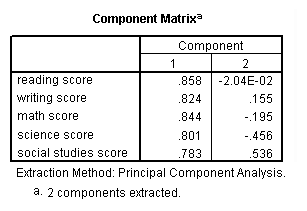
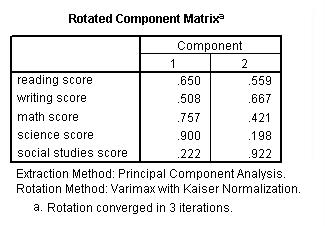
Factor analysis is a form of exploratory multivariate analysis that is used to either reduce the number of variables in a model or to detect relationships among variables. All variables involved in the factor analysis need to be interval and are assumed to be normally distributed. The goal of the analysis is to try to identify factors which underlie the variables. There may be fewer factors than variables, but there may not be more factors than variables. For our example using the hsb2 data file, let’s suppose that we think that there are some common factors underlying the various test scores. We will include subcommands for varimax rotation and a plot of the eigenvalues. We will use a principal components extraction and will retain two factors. (Using these options will make our results compatible with those from SAS and Stata and are not necessarily the options that you will want to use.)
factor /variables read write math science socst /criteria factors(2) /extraction pc /rotation varimax /plot eigen.
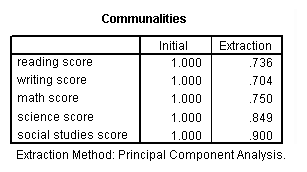
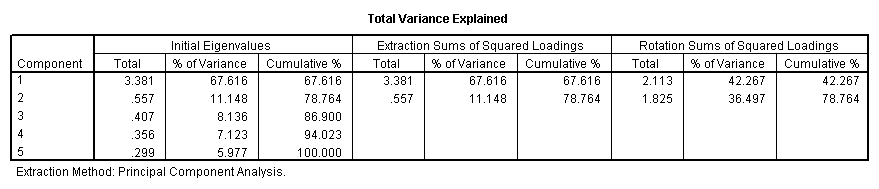
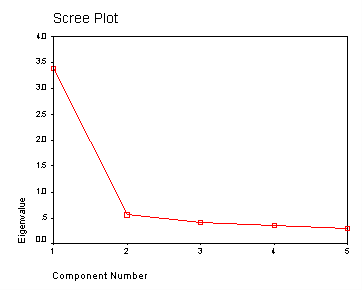
Communality (which is the opposite of uniqueness) is the proportion of variance of the variable (i.e., read) that is accounted for by all of the factors taken together, and a very low communality can indicate that a variable may not belong with any of the factors. The scree plot may be useful in determining how many factors to retain. From the component matrix table, we can see that all five of the test scores load onto the first factor, while all five tend to load not so heavily on the second factor. The purpose of rotating the factors is to get the variables to load either very high or very low on each factor. In this example, because all of the variables loaded onto factor 1 and not on factor 2, the rotation did not aid in the interpretation. Instead, it made the results even more difficult to interpret.
See also