Chapter Outline
-
1. Continuous and categorical predictors without interaction
-
2. Continuous and categorical predictors with interaction
-
3. Show slopes for each group
-
3.1 Show slopes by performing separate analyses
-
3.2 Show slopes for each group from one analysis
-
4. Compare slopes across groups
-
5. Simple effects and simple comparisons of group, strategy 1
-
5.1 Simple effects and comparisons when meals is 1 sd below mean
-
5.2 Simple effects and comparisons when meals is at the mean
-
5.3 Simple effects and comparisons when meals is 1 sd above the mean
-
6. Simple effects, simple group and interaction comparisons, strategy 2
-
7. More on predicted values
1.0 Continuous and Categorical Predictors without Interaction
Getting the data into SPSS and creating the variables icolcat2 and icolcat3 from using reverse Helmert coding on collcat. Then running the regression using the newly created variables.
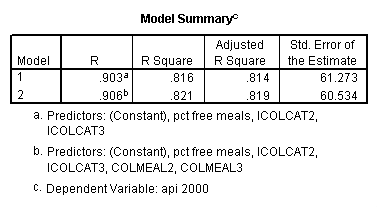
get file = "c:spssregelemapi2.sav". compute icolcat2 = 0. if (collcat=1) icolcat2 = -.5. if (collcat=2) icolcat2 = .5. compute icolcat3 = 2/3. if (collcat=1) icolcat3 = -1/3. if (collcat=2) icolcat3 = -1/3. execute. regression /dependent api00 /method = enter icolcat2 icolcat3 meals /save pred(predict1) .


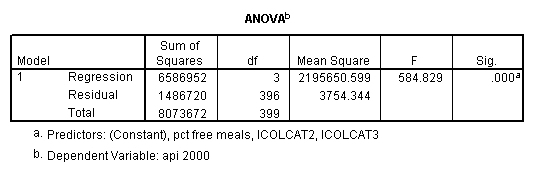
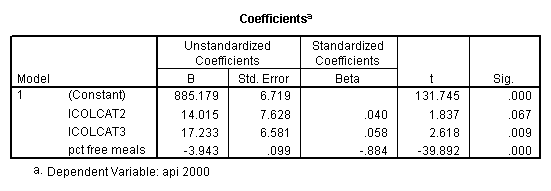
Graphing the regression lines for each of the levels of collcat.
graph /scatterplot(bivar)=meals with predict1 by collcat.
If you would like to print this in black and white and still be able to tell the lines apart it might be a good idea to change the symbols so that each line has a different symbol. To accomplish this double click on the graph in the output which will bring up the graph editor and now you have to click on a specific line (one of the collcat groups) inside the graph. Then you click on the format button in the top menu row and on the menu that drops down you select marker. In the marker menu you can select any symbol that you feel will differentiate the line from the others. You simply click on the symbol of your choice and then click on the apply button. Then you can click on a different line in the graph editor and then choose another symbol, click on the apply button and finally click on the close button and then close the graph editor window and all your modifications will appear in the graph in the output window.
2.0 Continuous and Categorical Predictors with Interaction
Creating the interactions of icolcat2 and icolcat3 with meals.
compute colmeal2 = icolcat2*meals. compute colmeal3 = icolcat3*meals. execute.
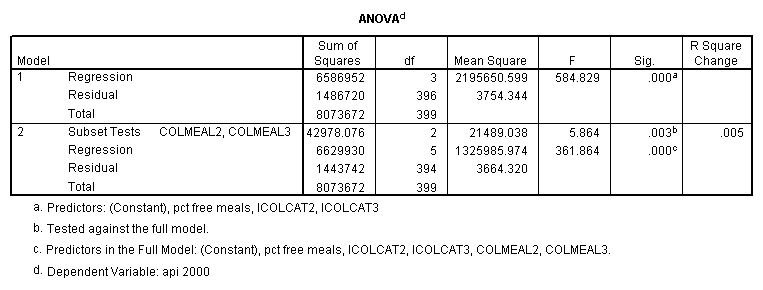
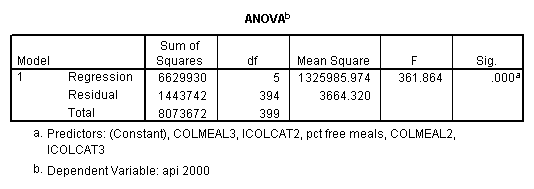
Testing the homogeneity of the slopes (the overall interaction effect) by looking at the second F-test (called Subset Tests) in the ANOVA table in the output with F=5.864 and p=.003. Some output has been omitted.
regression /dependent api00 /method=enter icolcat2 icolcat3 meals /method=test(colmeal2 colmeal3) /save= pred(predict2) .
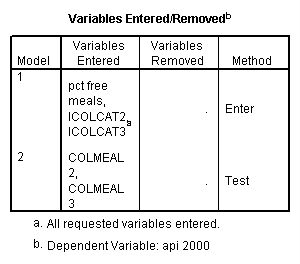
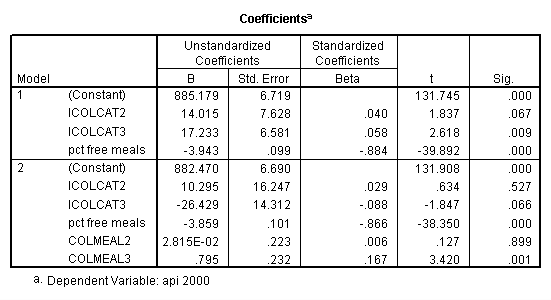
Graphing the regression lines for each of the levels of collcat. Notice that the lines are no longer parallel and that they cross between meals=20 and meals=40. Note: when the interaction is not included in the regression model the lines are forced to be parallel whereas when the interaction is include in the regression model the lines may cross as they do here.
graph /scatterplot(bivar)= meals with predict2 by collcat .
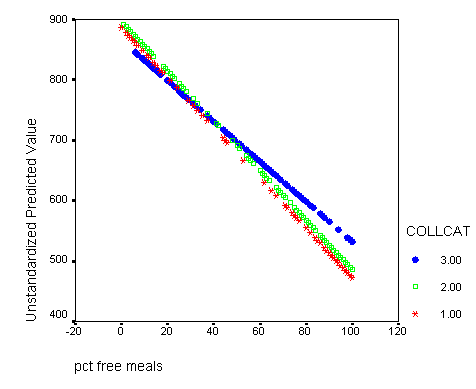
If you would like to print this in black and white and still be able to tell the lines apart it might be a good idea to change the symbols so that each line has a different symbol. To accomplish this double click on the graph in the output which will bring up the graph editor and now you have to click on a specific line inside the graph. Then you click on the format button in the top menu row and on the menu that drops down you select marker. In the marker menu you can select any symbol that you feel will differen tiate the line from the others. You simply click on the symbol of your choice and then click on the apply button. Then you can click on a different line in the graph editor and then choose another symbol, click on the apply button and finally click on the close button and then close the graph editor window and all your modifications will appear in the graph in the output window.
3.0 Obtaining slopes for each group
3.1 Obtaining slopes by separate analysis
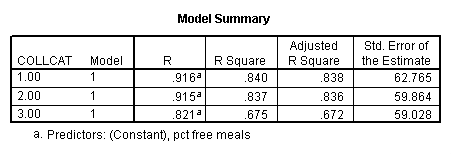
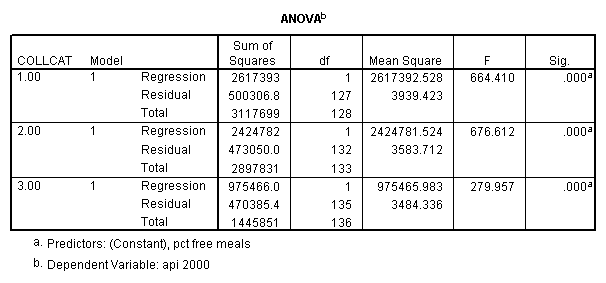
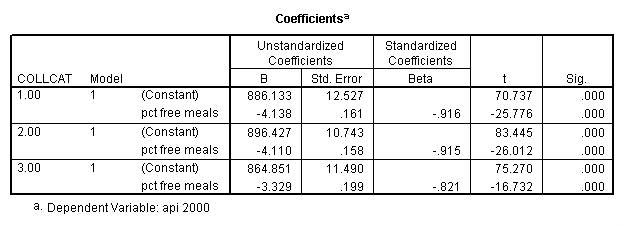
In order to run the regression for each level of collcat we must first sort the data set on collcat and then we temporarily split the file and run the regression model for each level of collcat by using the temporary command. Some output has been omitted.
sort cases by collcat . temporary . split file by collcat. regression /dependent=api00 /method=enter meals .
3.2 Obtaining slopes for each group in one analysis
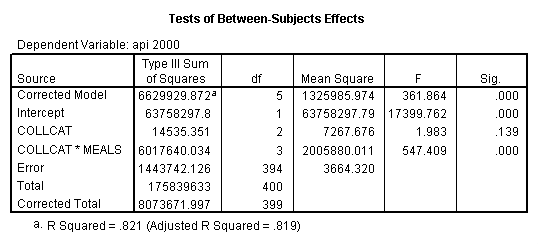
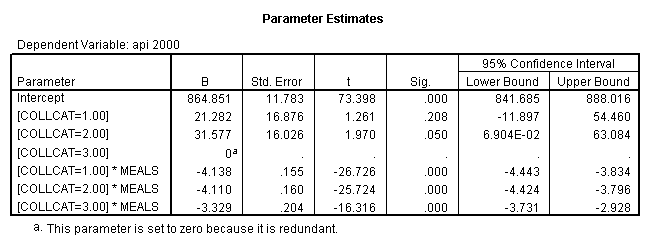
By using the design subcommand we can get the slopes for each of the groups in one analysis. The slopes that we are looking for are in the B column (the estimated parameter column) in the Parameter Estimate table.
glm api00 by collcat with meals /design collcat meals*collcat /print = parameter .

4.0 Comparing slopes across groups.
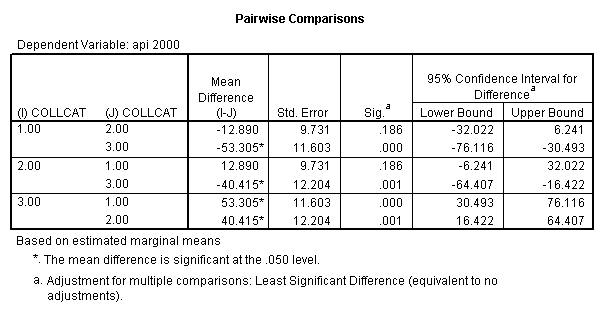
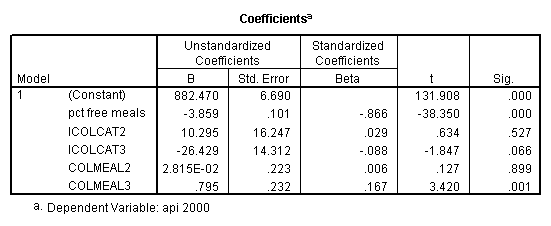
We can use the interactions of variables icolcat2 and icolcat3 and meals in order to compare slopes across groups in a regression. Then we can test the comparison of group 2 versus group 1 by looking at the test of the coefficient of the interaction of meals and icolcat2 (called colmeal2 in this model). Likewise, we can test the comparison of group3 versus groups 1,2 by looking at the coefficient of colmeal3 (which is the interaction of meals and icolcat3).
regression /dependent = api00 /method= enter meals icolcat2 icolcat3 colmeal2 colmeal3 .
5.0 Simple effects and simple comparisons, strategy 1
We shift the variable meals to be centered at its mean-1std, mean, and mean +1std. For each different centering we can test for simple effect of collcat. This corresponds to testing if there are differences in slopes at each of the vertical lines in the graph below. We would expect that at the mean-1std there would be no significant difference since in the graph the lines are all very close together. At the mean there could be a significant difference since the lines are more spaced out. At the mean +1std we expect group 3 to differ significantly from groups 1,2 since at this point the line for group 3 is far from the lines of groups 1 and 2 and the lines for those two groups are very close together. To get the numbers for the mean and the standard deviation of meals we use the descriptive command.
descriptives variables=meals /statistics=mean stddev min max .

The graph with the lines indicating at which values of meals that we will be comparing the groups.
graph /scatterplot(bivar)= meals with predict2 by collcat.
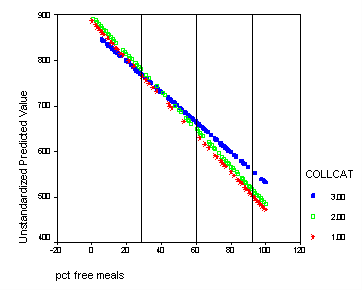
Do all the manipulations from before and now we are going to add reference lines at meals=mean-1 std, meals=mean, meals=mean+1 std. From the descriptive statistics of meals we find that mean-1 std = 60.3 – 31.9 = 28.4 and mean = 60.3, and mean +1std = 60.3 + 31.9 = 92.2. Double click on the graph in the output to bring up the graph editor. Then click on the chart button in the top row which brings up a menu where you click on Reference line. We want lines that are perpendicular to the x-axis so we choose x-axis which is the default and click on the OK button. Now you enter the three numbers: 28.4, 60.3, 92.2 in the in the Position of Lines box and click Add after EACH one so that they all appear in the box bellow. Then click OK and close the graph editor and all the changes will appear in the graph in the output.
5.1 Simple effects and comparisons when meals is 1 sd below mean
- Step 1: Recode meals and interactions to new center (=mean-1std) for the regression.
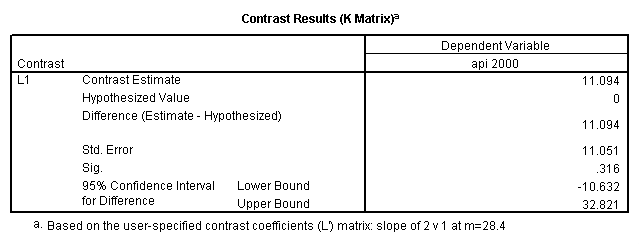
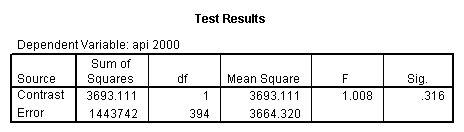
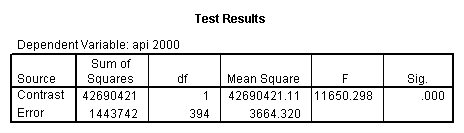
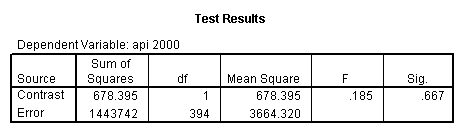
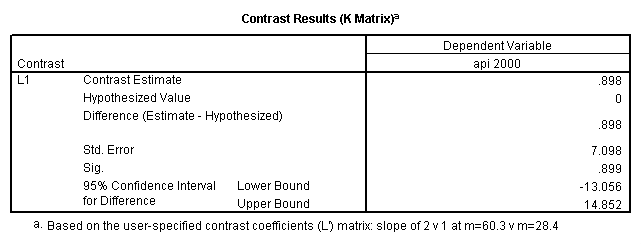
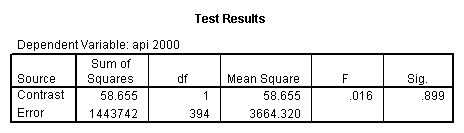
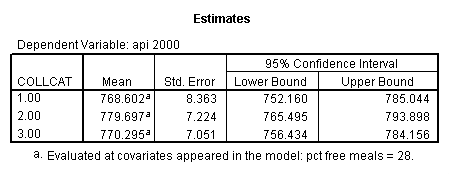
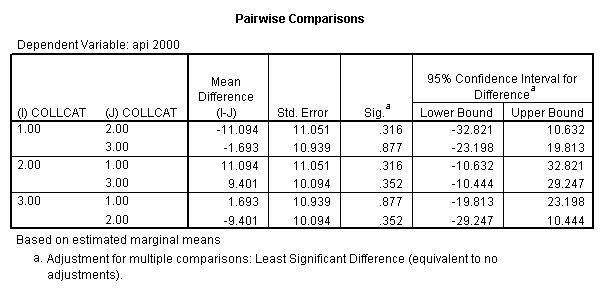
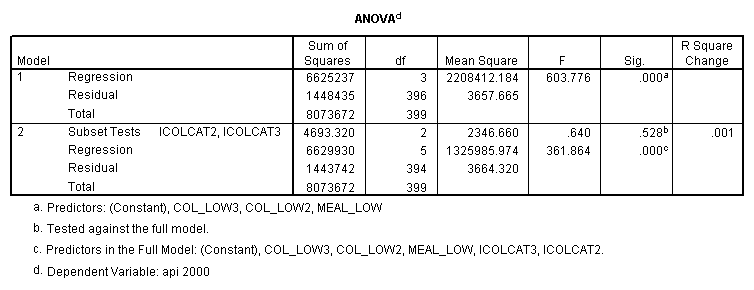
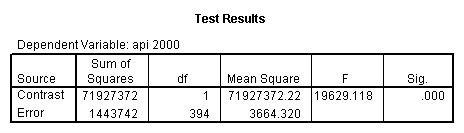
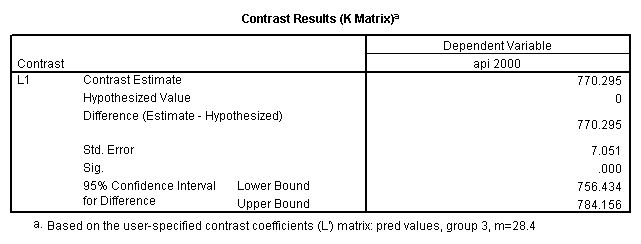
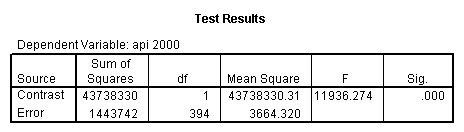
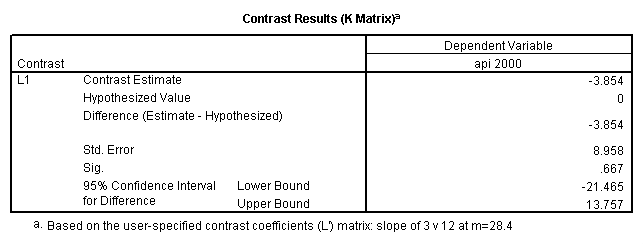
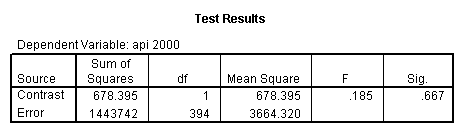
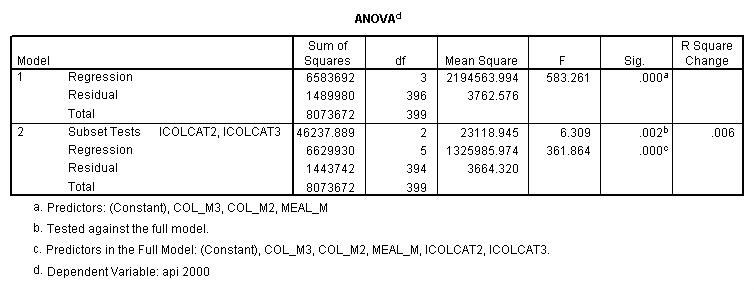
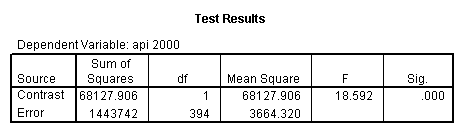
- Step 2: Run the regression command and test the overall effect of collcat. The result of the F test of the overall effect of collcat is labeled Subset Tests in the Anova table (F=.640 and p=.528). If the variables were coded to reflect specific contrasts then the tests of these contrasts will be the t-tests in the Coefficients table. I.e., if we want a simple comparison of collcat 2 versus 1 at meals=28.4 then we just look at the test for icollcat2.
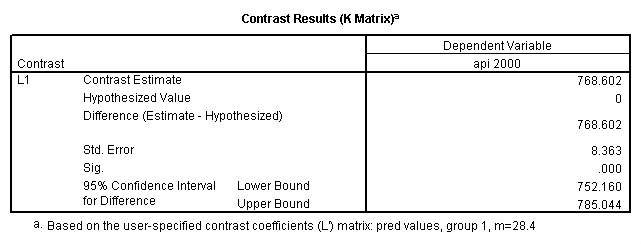
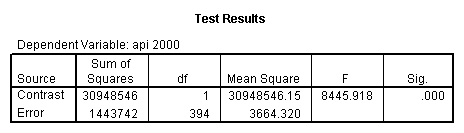
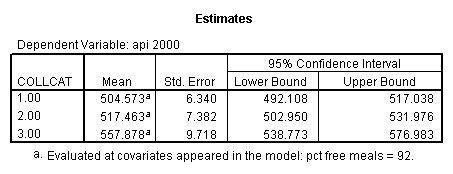
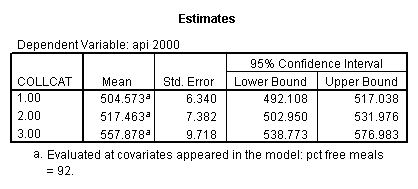
- Step 3: In the glm command we are able to obtain the simple comparisons at meals=mean-1 std, as well as the predicted means for each group of collcat. Some output has been omitted.
compute meal_low = meals - 28.4 . compute col_low2 = icolcat2*meal_low . compute col_low3 = icolcat3*meal_low . execute.
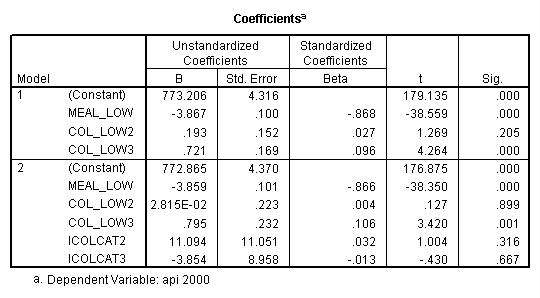
regression /dependent api00 /method=enter meal_low col_low2 col_low3 /method=test(icolcat2 icolcat3) .
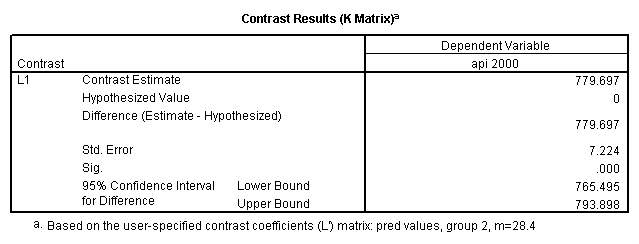
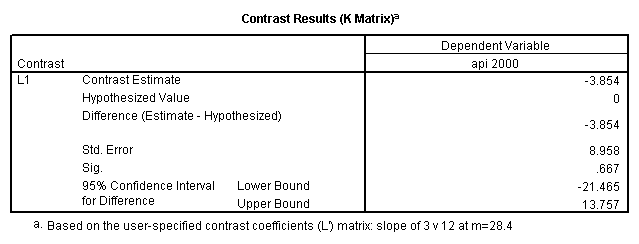
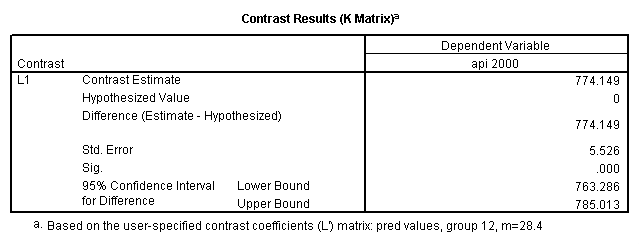
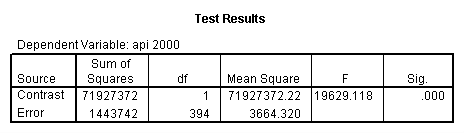
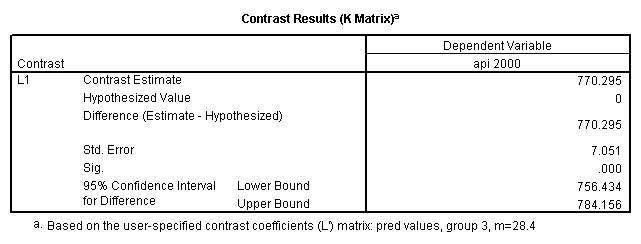
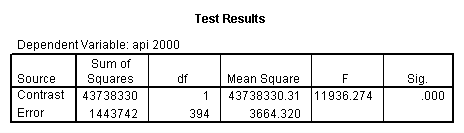
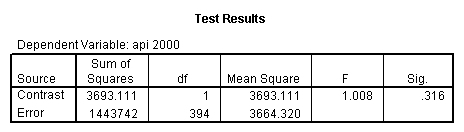
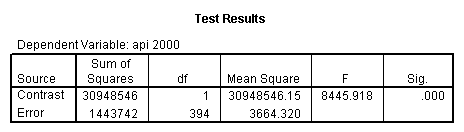
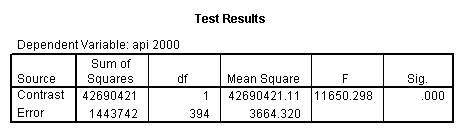
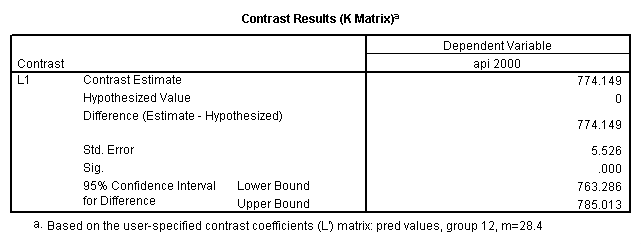
Reproducing the results of the regression using the glm command. For each contrast tested in the lmatrix subcommand the label of the test is in a footnote below the Contrast Results (K Matrix) table. Some output has been omitted.
Note: The lmatrix and emmeans subcommands overlap in the output they will provide. Here is a list of the different items that each subcommand will provide you with.
emmeans:
- 1. Predicted values for each group of collcat (in one command you get all of them at once).
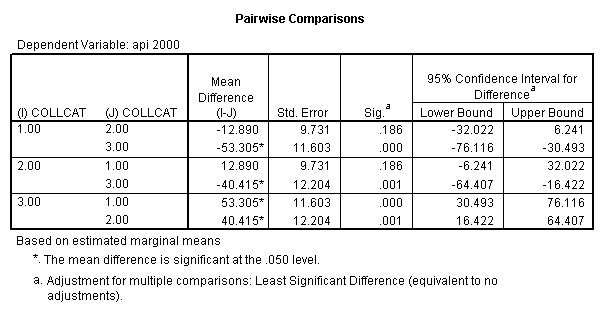
- 2. Pair-wise comparisons of groups of collcat at specified value of meals (in this example, meals=28.4).
- 3. Test of the overall effect of collcat.
lmatrix:
- 1. Predicted values of each group of collcat (you have to code an lmatrix subcommand for each predicted value separately).
- 2. Any simple contrast of groups of collcat at any value of meals (in this example all the lmatrix subcommands use meals=28.4 but you can use any value of meals within the same glm command).
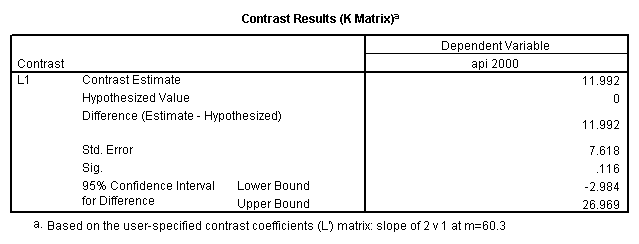
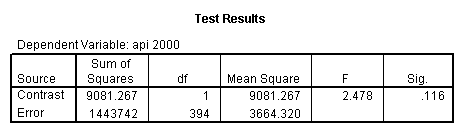
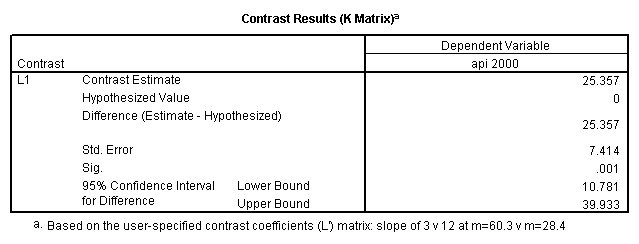
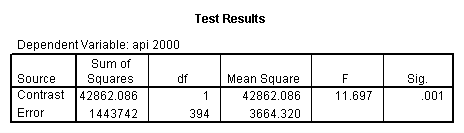
glm api00 by collcat with meals /design collcat meals meals*collcat /lmatrix 'slope of 2 v 1 at m=28.4' collcat -1 1 0 collcat*meals -28.4 28.4 0 /lmatrix 'pred values, group 1, m=28.4' intercept 1 meals 28.4 collcat 1 0 0 collcat*meals 28.4 0 0 /lmatrix 'pred values, group 2, m=28.4' intercept 1 meals 28.4 collcat 0 1 0 collcat*meals 0 28.4 0 /lmatrix 'pred values, group 12, m=28.4' intercept 1 meals 28.4 collcat .5 .5 0 collcat*meals 14.2 14.2 0 /lmatrix 'pred values, group 3, m=28.4' intercept 1 meals 28.4 collcat 0 0 1 collcat*meals 0 0 28.4 /lmatrix'slope of 3 v 12 at m=28.4' collcat -.5 -.5 1 collcat*meals -14.2 -14.2 28.4 emmeans = tables(collcat) with(meals=28.4) compare.




5.2 Simple effects and comparisons at meals=mean
- Step 1: Recode meal and interactions to new center (=mean-1std) for the regression.
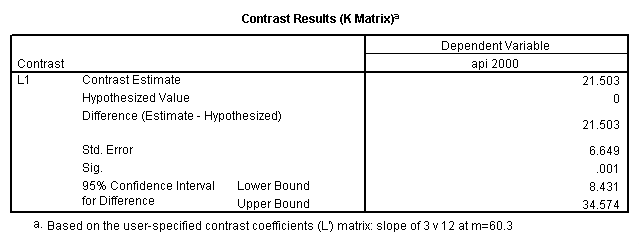
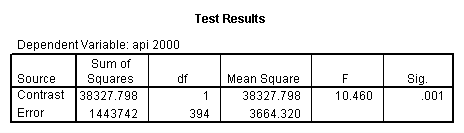
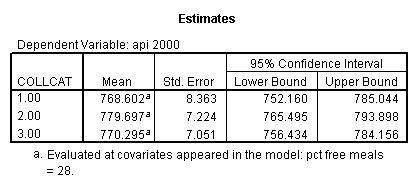
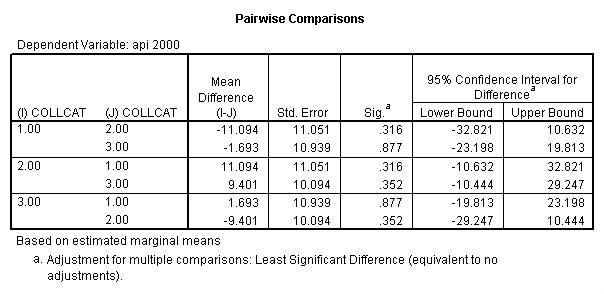
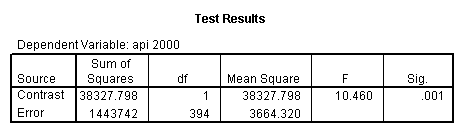
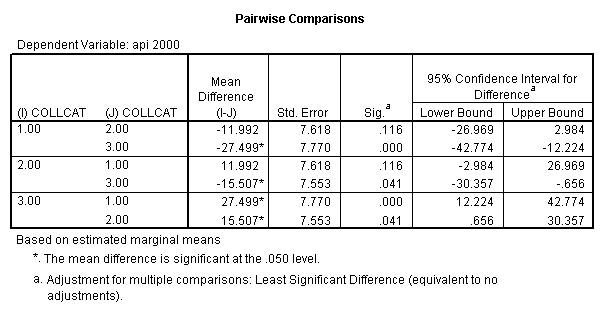
- Step 2: Run the regression command and test the overall effect of collcat. The result of the F test of the overall effect of collcat is labeled Subset Tests in the Anova table (F=6.309 and p=.002). If the variables were coded to reflect specific contrasts then the tests of these contrasts will be the t-tests in the Coefficients table. I.e., if we want a simple comparison of collcat 2 versus 1 at meals=60.3 then we just look at the test for icollcat2.
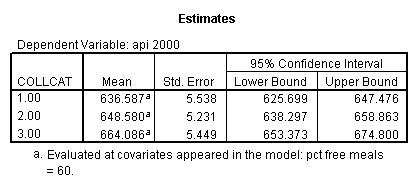
- Step 3: In the glm command we are able to obtain the simple comparisons at meals=mean-1 std, as well as the predicted means for each group of collcat. Some output has been omitted.
compute meal_m = meals - 60.3 . compute col_m2 = icolcat2*meal_m . compute col_m3 = icolcat3*meal_m . execute.
regression /dependent api00 /method=enter meal_m col_m2 col_m3 /method=test(icolcat2 icolcat3) .
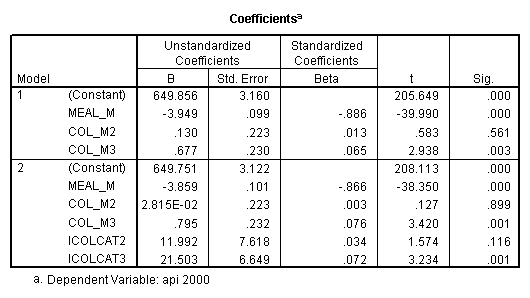
Reproducing the results of the regression using the glm command. For each contrast tested in the lmatrix subcommand the label of the test is in a footnote below the Contrast Results (K Matrix) table. Some output has been omitted. Note: The lmatrix and emmeans subcommands overlap in the output they will provide. Here is a list of the different items that each subcommand will provide you with.
emmeans:
- 1. Predicted values for each group of collcat (in one command you get all of them at once).
- 2. Pair-wise comparisons of groups of collcat at specified value of meals (in this example, meals=28.4).
- 3. Test of the overall effect of collcat.
lmatrix:
- 1. Predicted values of each group of collcat (you have to code an lmatrix subcommand for each predicted value separately).
- 2. Any simple contrast of groups of collcat at any value of meals (in this example all the lmatrix subcommands use meals=28.4 but you can use any value of meals within the same glm command).
glm api00 by collcat with meals /design collcat meals meals*collcat /lmatrix 'slope of 2 v 1 at m=60.3' collcat -1 1 0 collcat*meals -60.3 60.3 0 /lmatrix 'slope of 3 v 12 at m=60.3' collcat -.5 -.5 1 collcat*meals -30.15 -30.15 60.3 /emmeans = tables(collcat) with(meals=60.3) compare .
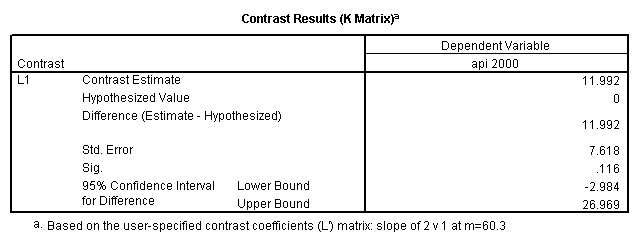
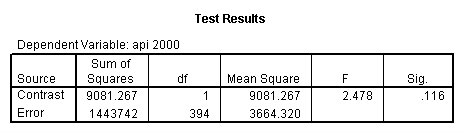
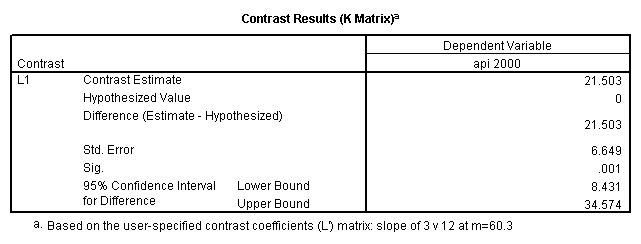

5.3 Simple effects and comparisons at meals=mean+1std
- Step 1: Recode meals and interactions to new center (=mean-1std) for the regression.
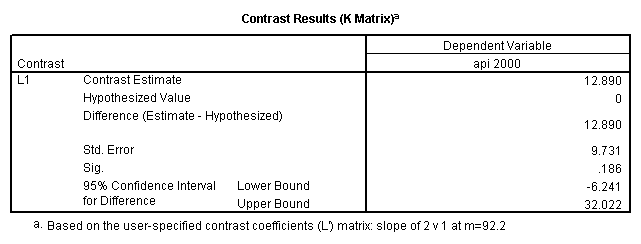
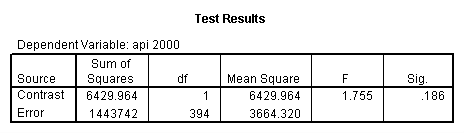
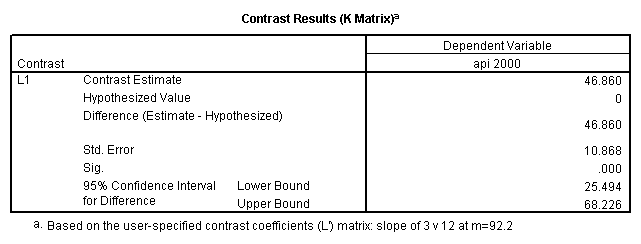
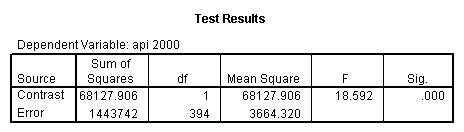
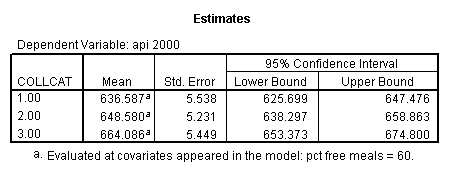
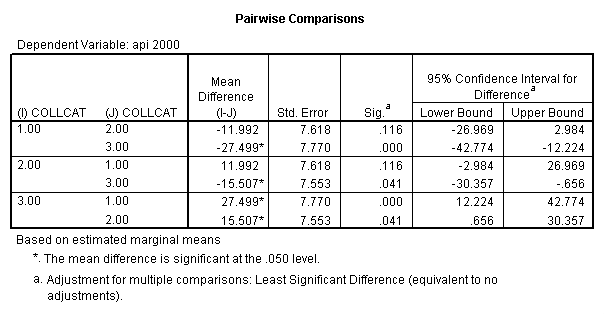
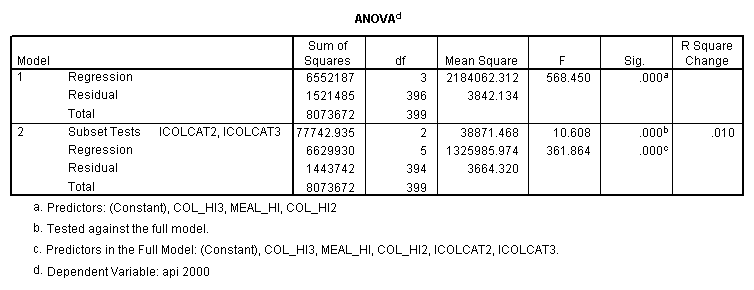
- Step 2: Run the regression command and test the overall effect of collcat. The result of the F test of the overall effect of collcat is labeled Subset Tests in the Anova table (F=10.608 and p=.000). If the variables were coded to reflect specific contrasts then the tests of these contrasts will be the t-tests in the Coefficients table. I.e., if we want a simple comparison of collcat 2 versus 1 at meals=92.2 then we just look at the test for icollcat2.
- Step 3: In the glm command we are able to obtain the simple comparisons at meals=mean-1 std, as well as the predicted means for each group of collcat. Some output has been omitted.
compute meal_hi = meals - 92.2 . compute col_hi2 = icolcat2*meal_hi . compute col_hi3 = icolcat3*meal_hi . execute. regression /dependent api00 /method=enter meal_hi col_hi2 col_hi3 /method=test(icolcat2 icolcat3) .
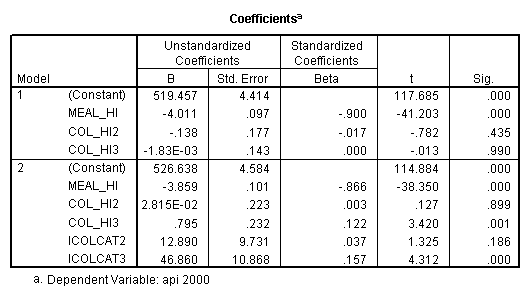
Reproducing the results of the regression using the glm command. For each contrast tested in the lmatrix subcommand the label of the test is in a footnote below the Contrast Results (K Matrix) table. Some output has been omitted.
Note: The lmatrix and emmeans subcommands overlap in the output they will provide. Here is a list of the different items that each subcommand will provide you with.
emmeans:
- 1. Predicted values for each group of collcat (in one command you get all of them at once).
- 2. Pair-wise comparisons of groups of collcat at specified value of meals (in this example, meals=28.4).
- 3. Test of the overall effect of collcat.
lmatrix:
- 1. Predicted values of each group of collcat (you have to code an lmatrix subcommand for each predicted value separately).
- 2. Any simple contrast of groups of collcat at any value of meals (in this example all the lmatrix subcommands use meals=28.4 but you can use any value of meals within the same glm command).
glm api00 by collcat with meals /design collcat meals meals*collcat /lmatrix 'slope of 2 v 1 at m=92.2' collcat -1 1 0 collcat*meals -92.2 92.2 0 /lmatrix 'slope of 3 v 12, m=92.2' collcat -.5 -.5 1 collcat*meals -46.1 -46.1 92.2 /emmeans = tables(collcat) with(meals=92.2) compare.
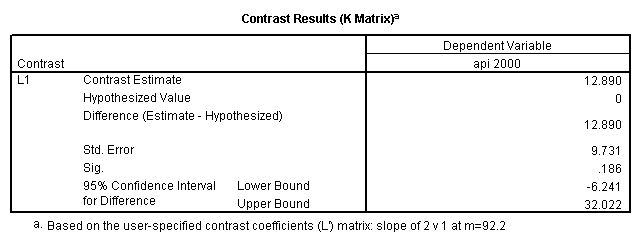
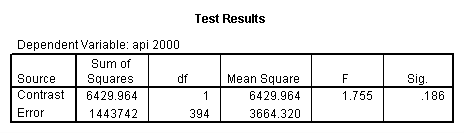
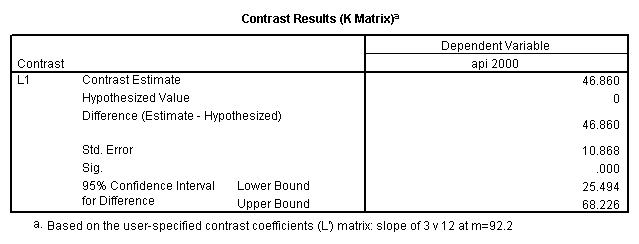

6. Simple effects, simple group and interaction comparisons, strategy 2
Getting all the information from the preceding regression and glm models but this time we get everything in one shot. Since we will use both the lmatrix and emmeans subcommands some of the output will be redundant (see section 5). To keep track of which part of the output corresponds to which part of the code it is advisable to look at the notes below the tables. For the output of the lmatrix subcommand this is where SPSS will state the label from the lmatrix subcommand. For the output of the emmeans subcommand this is where SPSS will specify the value of the continuous variable, in this example the specified value of meals. Some output has been omitted.
glm api00 by collcat with meals /design collcat meals meals*collcat /emmeans = tables(collcat) with(meals=28.4) compare /lmatrix 'slope of 2 v 1 at m=28.4' collcat -1 1 0 collcat*meals -28.4 28.4 0 /lmatrix 'pred values, group 1, m=28.4' intercept 1 meals 28.4 collcat 1 0 0 collcat*meals 28.4 0 0 /lmatrix 'pred values, group 2, m=28.4' intercept 1 meals 28.4 collcat 0 1 0 collcat*meals 0 28.4 0 /lmatrix 'slope of 3 v 12 at m=28.4' collcat -.5 -.5 1 collcat*meals -14.2 -14.2 28.4 /lmatrix 'pred values, group 12, m=28.4' intercept 1 meals 28.4 collcat .5 .5 0 collcat*meals 14.2 14.2 0 /lmatrix 'pred values, group 3, m=28.4' intercept 1 meals 28.4 collcat 0 0 1 collcat*meals 0 0 28.4 /emmeans = tables(collcat) with(meals=60.3) compare /lmatrix 'slope of 2 v 1 at m=60.3' collcat -1 1 0 collcat*meals -60.3 60.3 0 /lmatrix 'slope of 3 v 12 at m=60.3' collcat -.5 -.5 1 collcat*meals -30.15 -30.15 60.3 /emmeans = tables(collcat) with(meals=92.2) compare /lmatrix 'slope of 2 v 1 at m=92.2' collcat -1 1 0 collcat*meals -92.2 92.2 0 /lmatrix 'slope of 3 v 12 at m=92.2' collcat -.5 -.5 1 collcat*meals -46.1 -46.1 92.2 /lmatrix 'slope of 2 v 1 at m=60.3 v m=28.4' collcat*meals -31.9 31.9 0 /lmatrix 'slope of 3 v 12 at m=60.3 v m=28.4' collcat*meals -15.95 -15.95 31.9.