Introduction
Power analysis is the name given to the process for determining the sample size for a research study. The technical definition of power is the probability of detecting a "true" effect when it exists. Many students think that there is a simple formula for determining sample size for every research situation. However, the reality is that there are many research situations that are so complex that they almost defy rational power analysis. In most cases, power analysis involves making simplifying assumptions that make the problem tractable and running the analyses numerous times with different variations to cover all of the contingencies.
In this unit we will try to illustrate how to do a power analysis for a test of two independent proportions, i.e., the response variable has two levels and the predictor variable also has two levels. Instead of analyzing these data using a test of independent proportions, we could compute a chi-square statistic in a 2×2 contingency table or run a simple logistic regression analysis. These three analyses yield the same results and would require the same sample sizes to test effects.
Description of the experiment
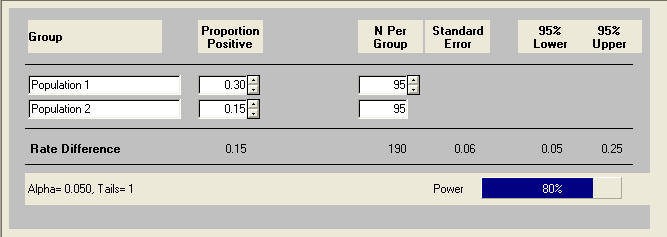
It is known that a certain type of skin lesion will develop into cancer in 30% of patients if left untreated. There is a drug on the market that will reduce the probability of cancer developing by 10%. A pharmaceutical company is developing a new drug to treat skin lesions but it will only be worthwhile to do so if the new drug is at least 5% better than the existing drug. The pharmaceutical company plans to do a study with patients randomly assigned to two groups, the control (untreated) group and the treatment group. The company wants to know how many subjects will be needed to test a difference in proportions of .15 with a power of .8 at alpha equal to .05.
We will make use of a Sample Power ‘2×2 for independent samples (Chi-squared or Fischer’s exact test)’ procedure, under the ‘Proportions’ tab in the Procedures catalog.
To proceed, we will need to provide the following information:
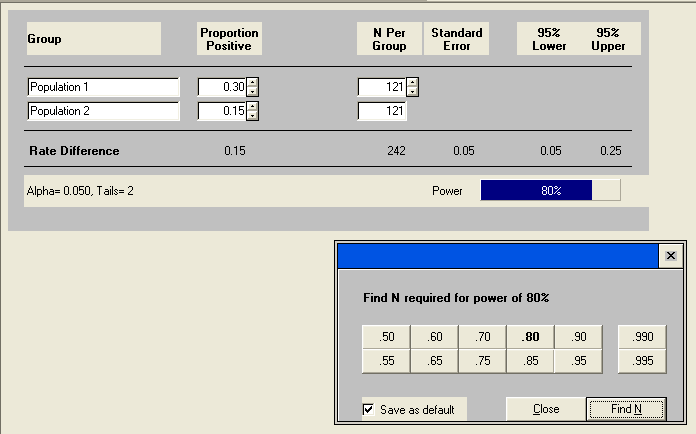
(accessible via the ‘Find N for any power’ button).
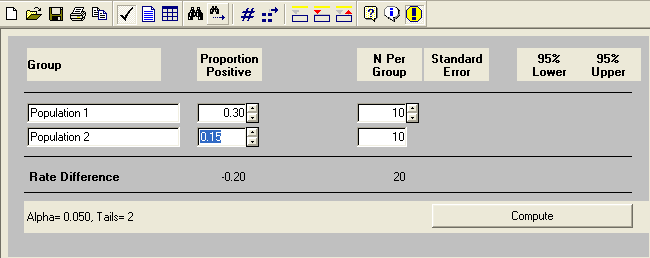
This is all well and good, but a two-sided test doesn’t make much sense in this situation. We want to test for a drug that reduces the probability of cancer not for one that increases the probability. In this case we should be using one-tail test and we do this by using the clicking "Tails=2" in the lower left-hand corner and selecting the one-tailed option.
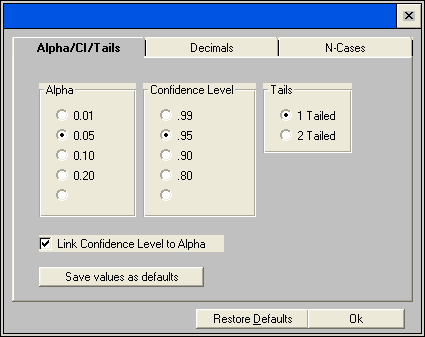
This is better. The result indicates that we need to use 95 subjects in each group to find a change in probability of .15 for a power of .8 when alpha equals .05
Because we believe that we know a lot about the incidence of cancer in the untreated group, we would like to make the control group half as large as the treatment group. By clicking on the ‘N Per Group’ column header, we open an options window allowing us to adjust the ratio between sample sizes. By setting ‘Link Sample Size in two groups’ on with cases in a ratio of 1 to 2, we ensure that the treatment group will be twice the control.
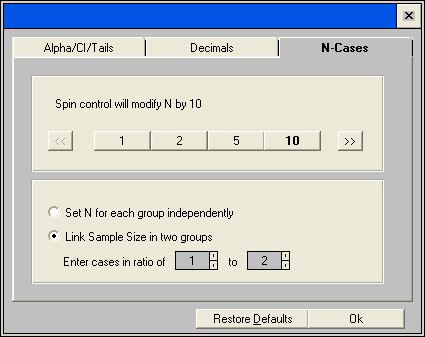
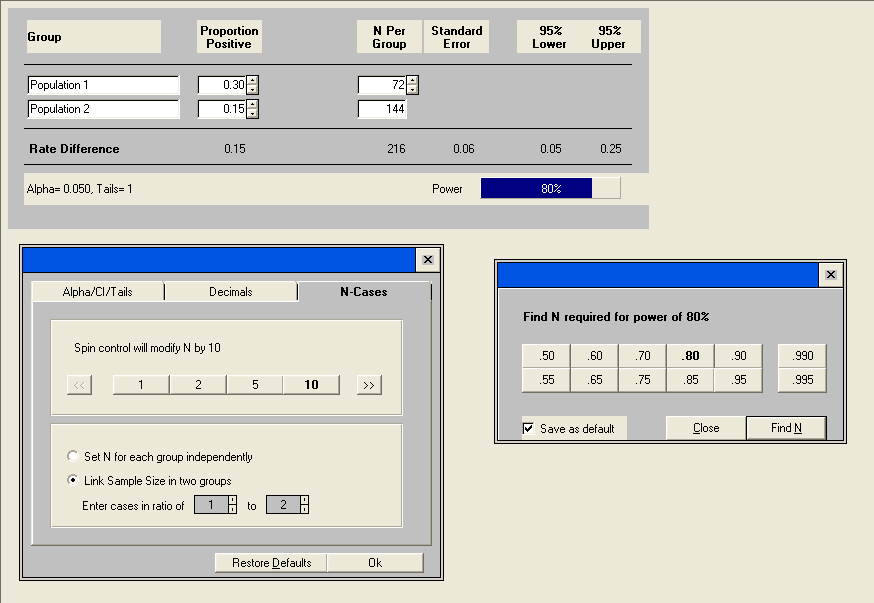
As you can see, we will need more subjects overall than for equal sized groups but we can have a much smaller untreated group.
In the end, the company has decided to use 75 patients in the control group and 150 in the treatment group. Let’s see what the power is.

With this unbalanced design we have an estimated power of .82 which the company deems acceptable.
For more information on power analysis, please visit our Introduction to Power Analysis seminar.