This page shows an example of multivariate analysis of variance (manova) in SPSS with footnotes explaining the output. The data used in this example are from the following experiment.
A researcher randomly assigns 33 subjects to one of three groups. The first group receives technical dietary information interactively from an on-line website. Group 2 receives the same information from a nurse practitioner, while group 3 receives the information from a video tape made by the same nurse practitioner. Each subject then made three ratings: difficulty, usefulness, and importance of the information in the presentation. The researcher looks at three different ratings of the presentation (difficulty, usefulness and importance) to determine if there is a difference in the modes of presentation. In particular, the researcher is interested in whether the interactive website is superior because that is the most cost-effective way of delivering the information. In the dataset, the ratings are presented in the variables useful, difficulty and importance. The variable group indicates the group to which a subject was assigned.
We are interested in how the variability in the three ratings can be explained by a subject’s group. Group is a categorical variable with three possible values: 1, 2 or 3. Because we have multiple dependent variables that cannot be combined, we will choose to use manova. Our null hypothesis in this analysis is that a subject’s group has no effect on any of the three different ratings, and we can test this hypothesis on the dataset, manova.sav.
GET FILE='C:\temp\manova.sav'.
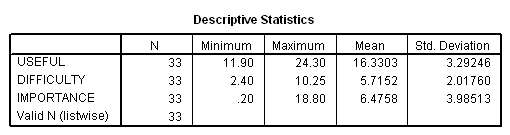
We can start by examining the three outcome variables.
DESCRIPTIVES VARIABLES=useful difficulty importance.
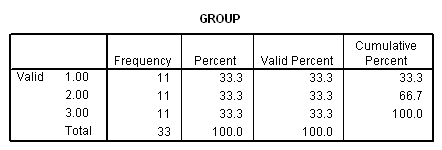
FREQUENCIES VARIABLES=group.

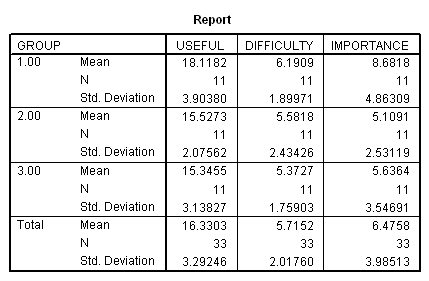
MEANS TABLES=useful difficulty importance BY group.
Next, we can enter our manova command. In SPSS, manova can be conducted through the generalized linear model function, GLM. In the manova command, we first list the outcome variables, then indicate any categorical factors after “by” and any covariates after “with”. Here, group is a categorical factor. We must also indicate the lowest and highest values found in group. We are also asking SPSS to print the eigenvalues generated. These will be useful in seeing how the test statistics are calculated.
manova useful difficulty importance by group(1,3) /print=sig(eigen).
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The default error term in MANOVA has been changed from WITHIN CELLS to
WITHIN+RESIDUAL. Note that these are the same for all full factorial
designs.
* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *
33 cases accepted.
0 cases rejected because of out-of-range factor values.
0 cases rejected because of missing data.
3 non-empty cells.
1 design will be processed.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *
EFFECT .. GROUP
Multivariate Tests of Significance (S = 2, M = 0, N = 13 )
Test Name Value Approx. F Hypoth. DF Error DF Sig. of F
Pillais .47667 3.02483 6.00 58.00 .012
Hotellings .89723 4.03753 6.00 54.00 .002
Wilks .52579 3.53823 6.00 56.00 .005
Roys .47146
Note.. F statistic for WILKS' Lambda is exact.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Eigenvalues and Canonical Correlations
Root No. Eigenvalue Pct. Cum. Pct. Canon Cor.
1 .892 99.416 99.416 .687
2 .005 .584 100.000 .072
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
EFFECT .. GROUP (Cont.)
Univariate F-tests with (2,30) D. F.
Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F
USEFUL 52.92424 293.96544 26.46212 9.79885 2.70053 .083
DIFFICUL 3.97515 126.28728 1.98758 4.20958 .47216 .628
IMPORTAN 81.82969 426.37090 40.91485 14.21236 2.87882 .072
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Abbreviated Extended
Name Name
DIFFICUL DIFFICULTY
IMPORTAN IMPORTANCE
Manova Output
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The default error term in MANOVA has been changed from WITHIN CELLS to
WITHIN+RESIDUAL. Note that these are the same for all full factorial
designs.
* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *
33 cases accepted.
0 cases rejected because of out-of-range factor values.
0 cases rejected because of missing data.
3 non-empty cells.
1 design will be processed.a
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *
EFFECTb .. GROUP
Multivariate Tests of Significance (S = 2, M = 0, N = 13 )
Test Name Valuec Approx. Fd Hypoth. DFe Error DFf Sig. of Fg
Pillaish .47667 3.02483 6.00 58.00 .012
Hotellingsi .89723 4.03753 6.00 54.00 .002
Wilksj .52579 3.53823 6.00 56.00 .005
Roysk .47146
Note.. F statistic for WILKS' Lambda is exact.l
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Eigenvalues and Canonical Correlationsm
Root No. Eigenvalue Pct. Cum. Pct. Canon Cor.
1 .892 99.416 99.416 .687
2 .005 .584 100.000 .072
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
EFFECT .. GROUP (Cont.)
Univariate F-tests with (2,30) D. F.n
Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F
USEFUL 52.92424 293.96544 26.46212 9.79885 2.70053 .083
DIFFICUL 3.97515 126.28728 1.98758 4.20958 .47216 .628
IMPORTAN 81.82969 426.37090 40.91485 14.21236 2.87882 .072
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Abbreviated Extended
Name Name
DIFFICUL DIFFICULTY
IMPORTAN IMPORTANCE
a. Case summary – This provides counts of the observations to be included in the manova and the counts of observations to be dropped due to missing data or data that falls out-of-range. For example, a record where the value for group is 4, after we have specified that the maximum value for group is 3, would be considered out-of-range.
b. Effect – This indicates the predictor variable in question. In our model, we are looking at the effect of group.
c. Value – This is the test statistic for the given effect and multivariate statistic listed in the prior column. For each predictor variable, SPSS calculates four test statistics. All of these test statistics are calculated using the eigenvalues of the model (see superscript m). See superscripts h, i, j and k for explanations of each of the tests.
d. Approx. F – This is the approximate F statistic for the given effect and test statistic.
e. Hypoth. DF – This is the number of degrees of freedom in the model.
f. Error DF – This is the number of degrees of freedom associated with the model errors. There are instances in manova when the degrees of freedom may be a non-integer.
g. Sig. of F – This is the p-value associated with the F statistic and the hypothesis and error degrees of freedom of a given effect and test statistic. The null hypothesis that a given predictor has no effect on either of the outcomes is evaluated with regard to this p-value. For a given alpha level, if the p-value is less than alpha, the null hypothesis is rejected. If not, then we fail to reject the null hypothesis. In this example, we reject the null hypothesis that group has no effect on the three different ratings at alpha level .05 because the p-values are all less than .05.
h. Pillais – This is Pillai’s Trace, one of the four multivariate criteria test statistics used in manova. We can calculate Pillai’s trace using the generated eigenvalues (see superscript m). Divide each eigenvalue by (1 + the eigenvalue), then sum these ratios. So in this example, you would first calculate 0.89198790/(1+0.89198790) = 0.471455394, 0.00524207/(1+0.00524207) = 0.005214734, and 0/(1+0)=0. When these are added, we arrive at Pillai’s trace: (0.471455394 + 0.005214734 + 0) = .47667.
i. Hotellings – This is Lawley-Hotelling’s Trace. It is very similar to Pillai’s Trace. It is the sum of the eigenvalues (see superscript m) and is a direct generalization of the F statistic in ANOVA. We can calculate the Hotelling-Lawley Trace by summing the characteristic roots listed in the output: 0.8919879 + 0.00524207 + 0 = 0.89723.
j. Wilks – This is Wilk’s Lambda. This can be interpreted as the proportion of the variance in the outcomes that is not explained by an effect. To calculate Wilks’ Lambda, for each eigenvalue, calculate 1/(1 + the eigenvalue), then find the product of these ratios. So in this example, you would first calculate 1/(1+0.8919879) = 0.5285446, 1/(1+0.00524207) = 0.9947853, and 1/(1+0)=1. Then multiply 0.5285446 * 0.9947853 * 1 = 0.52579.
k. Roys – This is Roy’s Largest Root. Note there are two definitions of Roy’s Largest Root depending on whether you use SPSS MANOVA or SPSS GLM. In MANOVA, the calculation is 0.8919879/(1+0.8919879) = 0.4714544. In GLM, Roy’s Largest root is defined as the largest eigenvalue, which is 0.8919879. Based on this definition, Roy’s Largest Root can behave differently from the other three test statistics. In instances where the other three are not significant and Roy’s is significant, the effect should be considered not significant. You can reference the following article for a detailed description of this discrepancy:
Kuhfeld, W. F. (1986). A note on Roy’s largest root. Psychometrika, 51(3), 479-481.
l. Note – This indicates that the F statistic for Wilk’s Lambda was calculated exactly. For the other test statistics, the F values are approximate (as indicated by the column heading).
m. Eigenvalues and Canonical Correlations – This section of output provides the eigenvalues from the product of the sum-of-squares matrix of the model and the sum-of-squares matrix of the errors. There is one eigenvalue for each of the three eigenvectors of the product of the model sum of squares matrix and the error sum of squares matrix, a 3×3 matrix. Because only two are listed here, we can assume the third eigenvalue is zero. These values can be used to calculate the four multivariate test statistics.
n. Univariate F-tests – The manova procedure provides both univariate and multivariate output. This section of output provides summarized output from a one-way anova for each of the outcomes in the manova. Each row corresponds to a different one-way anova, one for each dependent variable in the manova. While the manova tested a single hypothesis, each line in this output corresponds to a test of a different hypothesis. Generally, if your manova suggests that an effect is significant, you would expect at least one of these one-way anova tests to indicate that the effect is significant on a single outcome.
