This page is intended to be an example of common trend analysis in a repeated measures analysis. We will use data based on a real consulting problem we received. (We are grateful to Dr. Holly Hazlett-Stevens for giving us permission to use and adapt her data.) This page is not a comprehensive examination of how to perform a trend analysis in a repeated measures design, but is a summary of the advice we would give for this particular analysis. We will be using SAS proc glm and proc mixed.
This example is based on an experiment on 42 subjects who were randomly assigned to one of three groups (conditions, or cond), control (cond=1), treatment A (cond=2) and treatment B (cond=3). There were three dependent measures (ib, ms and sr) and they were each measured at five time points (e.g., ib1, ms1 and sr1 were all measured at time 1 and ib5, ms5 and sr5 were all measured at time 5). So this experiment has one between subjects variable (cond) and one repeated measures variable (time). The data are shown in the file repeat.txt.
The study predicts that the responses of the control group will not differ from those who received treatment A. However, it is also predicted that the responses of those who receive treatment B should differ from both the control group and the treatment A group. In particular, it is predicted that the responses of the treatment B group will tend to oscillate over the 5 time periods more than the other two groups. In other words, it is predicted that there will be an interaction between cond and time. The first 10 observations of the data set is included below.
Analysis 1: Standard between/within repeated analysis
We start with a standard analysis of variance that includes both a between subjects factor (condition) and a within subjects factor (time). First, we read the data as shown below and show a proc print of the first 10 observations as shown below.
options nocenter; data repeat; infile "repeat.txt"; input id cond ib1-ib5 ms1-ms5 sr1-sr5 ; run;
proc print data=repeat(obs=10); run;
The output of the proc print is shown below.
Obs id cond ib1 ib2 ib3 ib4 ib5 1 1 1 1415.94 1457.06 1484.38 1583.71 1603.07 2 2 3 1385.95 1550.62 1528.70 1541.53 1582.64 3 3 2 1211.38 1313.07 1326.06 1294.30 1411.97 4 4 2 1318.06 1350.23 1423.97 1386.87 1392.59 5 5 3 1648.54 1655.81 1672.03 1756.02 1758.25 6 6 3 1467.75 1506.05 1595.74 1675.13 1570.27 7 7 1 1627.09 1659.87 1734.72 1736.64 1756.33 8 8 3 1391.31 1362.23 1381.47 1585.56 1553.41 9 9 3 999.29 1127.63 1295.83 1400.72 1382.79 10 10 2 1600.34 1645.25 1665.01 1717.93 1722.37 Obs id cond ms1 ms2 ms3 ms4 ms5 1 1 1 64.71 51.04 54.40 86.96 90.23 2 2 3 36.51 50.29 47.32 43.08 46.45 3 3 2 61.08 71.80 76.45 72.78 79.32 4 4 2 28.75 29.64 39.95 31.05 33.89 5 5 3 88.97 90.67 87.73 91.87 104.56 6 6 3 71.59 66.88 78.89 100.50 76.31 7 7 1 109.85 97.48 122.51 122.40 139.64 8 8 3 . . . . . 9 9 3 22.20 48.71 57.71 61.36 76.34 10 10 2 78.60 69.38 74.36 79.24 82.49 Obs id cond sr1 sr2 sr3 sr4 sr5 1 1 1 8 7 5 5 6 2 2 3 14 15 17 17 16 3 3 2 18 18 18 16 17 4 4 2 16 15 11 13 14 5 5 3 9 11 10 12 11 6 6 3 13 15 14 11 9 7 7 1 10 11 11 9 9 8 8 3 15 16 13 13 11 9 9 3 13 10 4 11 10 10 10 2 13 11 13 13 11
Let’s do a standard between/within repeated measures ANOVA using SAS proc glm, with cond as a between subjects variable, and time as a within subjects variable.
PROC GLM DATA=repeat; class cond; model sr1-sr5 = cond ; repeated time 5 ; Run;
We show important excerpts of the output below.
Within-subjects results using MANOVA test method
Manova Test Criteria and Exact F Statistics for the Hypothesis of no time Effect
H = Type III SSCP Matrix for time
E = Error SSCP Matrix
S=1 M=1 N=17
Statistic Value F Value Num DF Den DF Pr > F
Wilks' Lambda 0.64788274 4.89 4 36 0.0030
Pillai's Trace 0.35211726 4.89 4 36 0.0030
Hotelling-Lawley Trace 0.54348918 4.89 4 36 0.0030
Roy's Greatest Root 0.54348918 4.89 4 36 0.0030
Manova Test Criteria and F Approximations for the Hypothesis of no time*cond Effect
H = Type III SSCP Matrix for time*cond
E = Error SSCP Matrix
S=2 M=0.5 N=17
Statistic Value F Value Num DF Den DF Pr > F
Wilks' Lambda 0.62780347 2.36 8 72 0.0259
Pillai's Trace 0.39613669 2.28 8 74 0.0303
Hotelling-Lawley Trace 0.55472196 2.46 8 49.161 0.0253
Roy's Greatest Root 0.47432775 4.39 4 37 0.0053
NOTE: F Statistic for Roy's Greatest Root is an upper bound.
NOTE: F Statistic for Wilks' Lambda is exact.
Between-subjects results
Repeated Measures Analysis of Variance Tests of Hypotheses for Between Subjects Effects Source DF Type III SS Mean Square F Value Pr > F cond 2 573.895238 286.947619 5.70 0.0067 Error 39 1962.528571 50.321245
Within-subjects results using UNIVARIATE test method
Repeated Measures Analysis of Variance
Univariate Tests of Hypotheses for Within Subject Effects
Adj Pr > F
Source DF Type III SS Mean Square F Value Pr > F G - G H - F
time 4 88.1142857 22.0285714 8.36 <.0001 0.0001 <.0001
time*cond 8 26.6285714 3.3285714 1.26 0.2669 0.2851 0.2807
Error(time) 156 411.2571429 2.6362637
Greenhouse-Geisser Epsilon 0.6496
Huynh-Feldt Epsilon 0.7358
Let’s examine these results, especially the within subjects results. Notice that the output shows two separate tests of the within subjects effects: one set of tests labeled the MANOVA tests and the other the UNIVARIATE tests. Now look at the results for the time by cond interaction. The UNIVARIATE tests give a p-value of 0.2669 (and adjusted values of .2851 and .2807) but the MANOVA tests give 4 p-values, repeated below.
Wilks' Lambda 0.62780347 2.36 8 72 0.0259 Pillai's Trace 0.39613669 2.28 8 74 0.0303 Hotelling-Lawley Trace 0.55472196 2.46 8 49.161 0.0253 Roy's Greatest Root 0.47432775 4.39 4 37 0.0053 NOTE: F Statistic for Roy's Greatest Root is an upper bound. NOTE: F Statistic for Wilks' Lambda is exact.These UNIVARIATE and MANOVA tests give quite different results. This is because the two tests make different assumptions about the nature of the correlations (or covariances) of the scores across time. The UNIVARIATE results assume homogeneity of variance across the trials (that the variance of the scores on each of the five trials are the same) and homogeneity of covariance (that the covariances among all of the pairs of trials are the same). This is a very strong assumption and can be easily and frequently violated. By contrast, the MANOVA tests are based on a much more realistic (but possibly overly complex) assumption about the variances and covariances. The MANOVA tests include a separate variance for each trial (in this case, a separate variance for each of the five trials), and a separate covariance for each of the pairs of trials, (i.e., 10 separate covariances). While this assumption may be overly complex and estimate many more variances and covariances than may be necessary, it is a more realistic assumption than the assumptions made by the UNIVARIATE tests.
As we compare the UNIVARIATE and MANOVA results, we are delighted that the MANOVA tests are significant, but can we really conclude that those results are the most appropriate to select. We cannot justify choosing those results simply because the MANOVA results are most favorable to us. Given the Univariate results make such an unrealistic and implausible assumption about the nature of the variances and covariances in the data, we would be more likely to choose the MANOVA results and will tentatively accept them. Later, we will look at ways to independently assess which covariance structure is the most appropriate.
In the meanwhile, if we wanted to report these results which significance test should we report. Should we pick Roy’s test because that has the best significance value? The output states that the Wilk’s Lambda is exact, so we would pick that as the value to report. So, based on the Wilks’ Lambda, we can say that there was a significant interaction between cond and time (p=.0259).
Let’s see how we could do these analyses in SPSS.
data list free file="repeat.txt" /id cond ib1 to ib5 ms1 to ms5 sr1 to sr5. GLM sr1 to sr5 by cond /wsfactors = time 5.
Excerpts of the SPSS output is shown below (you can view the entire output at an1b.htm). Although the output looks different from the SAS output in its formatting, if you look more closely you can see that the results shown in the output are quite identical to those from SAS. Like the SAS output, the SPSS output shows Multivariate (MANOVA) tests for the within subjects effects, and Univariate tests for the within subjects effects.
Within-subjects results using MANOVA test method
| Multivariate Testsa | ||||||
| Effect | Value | F | Hypothesis df | Error df | Sig. | |
| time | Pillai’s Trace | 0.352 | 4.891b | 4.000 | 36.000 | 0.003 |
| Wilks’ Lambda | 0.648 | 4.891b | 4.000 | 36.000 | 0.003 | |
| Hotelling’s Trace | 0.543 | 4.891b | 4.000 | 36.000 | 0.003 | |
| Roy’s Largest Root | 0.543 | 4.891b | 4.000 | 36.000 | 0.003 | |
| time * cond | Pillai’s Trace | 0.396 | 2.285 | 8.000 | 74.000 | 0.030 |
| Wilks’ Lambda | 0.628 | 2.359b | 8.000 | 72.000 | 0.026 | |
| Hotelling’s Trace | 0.555 | 2.427 | 8.000 | 70.000 | 0.022 | |
| Roy’s Largest Root | 0.474 | 4.388c | 4.000 | 37.000 | 0.005 | |
| a. Design: Intercept + cond Within Subjects Design: time | ||||||
| b. Exact statistic | ||||||
| c. The statistic is an upper bound on F that yields a lower bound on the significance level. | ||||||
Within-subjects results using UNIVARIATE test method
| Tests of Within-Subjects Effects | |||||||
| Measure: | |||||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. | ||
| time | Sphericity Assumed | 88.114 | 4 | 22.029 | 8.356 | 0.000 | |
| Greenhouse-Geisser | 88.114 | 2.599 | 33.909 | 8.356 | 0.000 | ||
| Huynh-Feldt | 88.114 | 2.943 | 29.937 | 8.356 | 0.000 | ||
| Lower-bound | 88.114 | 1.000 | 88.114 | 8.356 | 0.006 | ||
| time * cond | Sphericity Assumed | 26.629 | 8 | 3.329 | 1.263 | 0.267 | |
| Greenhouse-Geisser | 26.629 | 5.197 | 5.124 | 1.263 | 0.285 | ||
| Huynh-Feldt | 26.629 | 5.887 | 4.524 | 1.263 | 0.281 | ||
| Lower-bound | 26.629 | 2.000 | 13.314 | 1.263 | 0.294 | ||
| Error(time) | Sphericity Assumed | 411.257 | 156 | 2.636 | |||
| Greenhouse-Geisser | 411.257 | 101.345 | 4.058 | ||||
| Huynh-Feldt | 411.257 | 114.789 | 3.583 | ||||
| Lower-bound | 411.257 | 39.000 | 10.545 | ||||
Between-subjects results
| Tests of Between-Subjects Effects | ||||||
| Measure: | ||||||
| Transformed Variable: | ||||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. | |
| Intercept | 29976.576 | 1 | 29976.576 | 595.704 | 0.000 | |
| cond | 573.895 | 2 | 286.948 | 5.702 | 0.007 | |
| Error | 1962.529 | 39 | 50.321 | |||
Analysis 2: Add trend analysis on time
The tests from Analysis 1 did assess whether there was an interaction between cond and time, but it did not assess this very precisely. There are many possible patterns of data that could produce such an interaction, many of which would not be consistent with the main hypothesis. To perform a more precise test, we will do a trend analysis of the time variable, and look at the interactions of these trend components of time by cond. We would predict that the higher orders of time (e.g., time^3 or time^4) would interact with cond (because we predict the Treatment B group will oscillate more over time than the other groups). This analysis is shown below. The polynomial / summary asks for the trend analysis on time.
PROC GLM DATA=repeat; class cond; model sr1-sr5 = cond ; repeated time 5 polynomial / summary ; Run;
The relevant results are shown below. The tests under time_1 refer to the linear effect of time. The results labeled Mean with F=19.78 indicate an overall linear effect of time. The results labeled cond with F=.69 indicate that the interaction of the linear effect of time by cond was not significant. Looking at the higher order effects (time_3 and time_4) we see that time_4 by cond is significant (F=4.96), indicating an interaction of time^4 by cond, as we predicted. We can think of time^4 as the tendency for the scores over time to exhibit 3 bends (like an M or like a W ), so a time^4 by cond interaction means that the conditions differ in their tendency to show 3 bends. This test more precisely reflects a test of our hypothesis than Analysis #1, however it is still ambiguous which groups are showing the greater tendency to oscillate. In Analysis #3, we will more precisely compare among the groups as stated by our hypotheses.
Repeated Measures Analysis of Variance Analysis of Variance of Contrast Variables time_N represents the nth degree polynomial contrast for time Contrast Variable: time_1 Source DF Type III SS Mean Square F Value Pr > F Mean 1 80.6095238 80.6095238 19.78 <.0001 cond 2 5.6333333 2.8166667 0.69 0.5071 Error 39 158.9571429 4.0758242 Contrast Variable: time_2 Source DF Type III SS Mean Square F Value Pr > F Mean 1 7.4081633 7.4081633 1.86 0.1800 cond 2 6.7448980 3.3724490 0.85 0.4358 Error 39 154.9897959 3.9740973 Contrast Variable: time_3 Source DF Type III SS Mean Square F Value Pr > F Mean 1 0.00952381 0.00952381 0.01 0.9331 cond 2 2.74761905 1.37380952 1.03 0.3667 Error 39 52.04285714 1.33443223 Contrast Variable: time_4 Source DF Type III SS Mean Square F Value Pr > F Mean 1 0.08707483 0.08707483 0.08 0.7856 cond 2 11.50272109 5.75136054 4.96 0.0121 Error 39 45.26734694 1.16070120
Let’s see how we could do these analyses in SPSS. Well, if we examine the output from the first analysis we would see this output that we overlooked in Analysis #1. As you can see by comparing these results from those shown above in SAS, these are the same results. By default, SPSS includes a trend analysis on the repeated measures factor (in this case, time) saving us from having to specifically request this analysis.
| Tests of Within-Subjects Contrasts | |||||||
| Measure: | |||||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. | ||
| time | Linear | 80.610 | 1 | 80.610 | 19.777 | 0.000 | |
| Quadratic | 7.408 | 1 | 7.408 | 1.864 | 0.180 | ||
| Cubic | 0.010 | 1 | 0.010 | 0.007 | 0.933 | ||
| Order 4 | 0.087 | 1 | 0.087 | 0.075 | 0.786 | ||
| time * cond | Linear | 5.633 | 2 | 2.817 | 0.691 | 0.507 | |
| Quadratic | 6.745 | 2 | 3.372 | 0.849 | 0.436 | ||
| Cubic | 2.748 | 2 | 1.374 | 1.030 | 0.367 | ||
| Order 4 | 11.503 | 2 | 5.751 | 4.955 | 0.012 | ||
| Error(time) | Linear | 158.957 | 39 | 4.076 | |||
| Quadratic | 154.990 | 39 | 3.974 | ||||
| Cubic | 52.043 | 39 | 1.334 | ||||
| Order 4 | 45.267 | 39 | 1.161 | ||||
Analysis 3: Add comparison on conditions
The tests from Analysis 2 indicated that there were differences in the amount of oscillation over time by cond, but we are specifically interested in seeing if Treatment B causes more oscillation than the Control and Treatment A (and we also predict the amount of oscillation should be the same for Control and Treatment A). We can form comparisons on cond to make these specific comparisons. Ordinarily, you would think to use the contrast statement for this analysis, however the contrasts would apply only to cond, but we want them to interact with time (and in particular, with the different trend components of time). We will create a new variable called cond1 that is 1 if it is Treatment B, and 0 if not. Comparisons that involve cond1 will directly compare Treatment B to the other 2 groups. Likewise, we will create a new variable called cond2 that will be 1 if Treatment A, 0 if Control, and missing if Treatment B. The variable cond2 directly compares Treatment A with the Control group. This is illustrated below.
data repeat2; set repeat; if cond = 1 or cond = 2 then cond1 = 1; if cond = 3 then cond1 = 2; if cond = 1 then cond2 = 1; if cond = 2 then cond2 = 2; if cond = 3 then cond2 = .; run;
PROC GLM DATA=repeat2; class cond1; model sr1-sr5 = cond1 ; repeated time 5 polynomial / summary nouni ; Run; PROC GLM DATA=repeat2; class cond2; model sr1-sr5 = cond2 ; repeated time 5 polynomial / summary nouni ; Run; quit;
The results from the first proc glm are shown below.
The GLM Procedure Repeated Measures Analysis of Variance Analysis of Variance of Contrast Variables time_N represents the nth degree polynomial contrast for time Contrast Variable: time_1 Source DF Type III SS Mean Square F Value Pr > F Mean 1 59.2011905 59.2011905 14.87 0.0004 cond1 1 5.3440476 5.3440476 1.34 0.2535 Error 40 159.2464286 3.9811607 Contrast Variable: time_2 Source DF Type III SS Mean Square F Value Pr > F Mean 1 2.9600340 2.9600340 0.76 0.3878 cond1 1 6.4362245 6.4362245 1.66 0.2053 Error 40 155.2984694 3.8824617 Contrast Variable: time_3 Source DF Type III SS Mean Square F Value Pr > F Mean 1 0.00119048 0.00119048 0.00 0.9766 cond1 1 0.14404762 0.14404762 0.11 0.7471 Error 40 54.64642857 1.36616071 Contrast Variable: time_4 Source DF Type III SS Mean Square F Value Pr > F Mean 1 1.94710884 1.94710884 1.71 0.1984 cond1 1 11.23282313 11.23282313 9.87 0.0032 Error 40 45.53724490 1.13843112
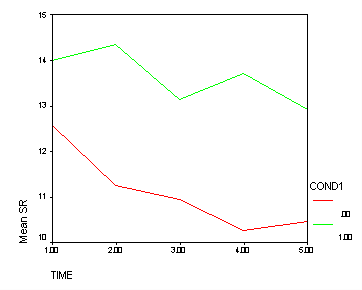
Looking in the section time_4 we see the cond1 effect is significant (F=9.87). Below we show a graph of this effect. The green line (Treatment B) clearly shows a greater tendency to have 3 bends (like an M) than the red line (Treatment A and Control combined). This is exactly the pattern that was hypothesized, and the n time_4 we see the cond1 effect tests for this pattern of results.
The results from the second proc glm are shown below.
The GLM Procedure Repeated Measures Analysis of Variance Analysis of Variance of Contrast Variables time_N represents the nth degree polynomial contrast for time Contrast Variable: time_1 Source DF Type III SS Mean Square F Value Pr > F Mean 1 75.0892857 75.0892857 18.26 0.0002 cond2 1 0.2892857 0.2892857 0.07 0.7929 Error 26 106.9214286 4.1123626 Contrast Variable: time_2 Source DF Type III SS Mean Square F Value Pr > F Mean 1 13.5943878 13.5943878 3.06 0.0920 cond2 1 0.3086735 0.3086735 0.07 0.7941 Error 26 115.4540816 4.4405416 Contrast Variable: time_3 Source DF Type III SS Mean Square F Value Pr > F Mean 1 0.08928571 0.08928571 0.06 0.8160 cond2 1 2.60357143 2.60357143 1.61 0.2155 Error 26 42.00714286 1.61565934 time_N represents the nth degree polynomial contrast for time Contrast Variable: time_4 Source DF Type III SS Mean Square F Value Pr > F Mean 1 2.86989796 2.86989796 3.32 0.0801 cond2 1 0.26989796 0.26989796 0.31 0.5813 Error 26 22.50306122 0.86550235
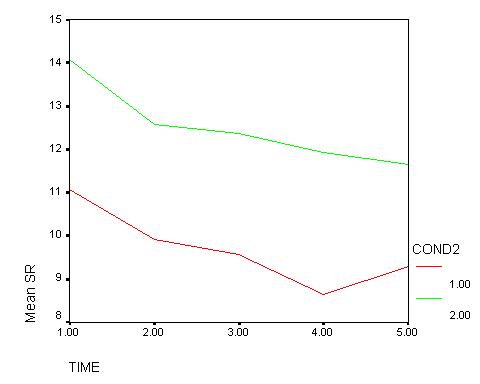
It was predicted that there would be no differences in the trend over time between Treatment A and the Control group. The results shown above are consistent with these predictions — the time1 by cond, time2 by cond, time3 by cond, and time4 by cond effects are all not significant. This is consistent with the graph shown below. The red line represents the control group, and the green line represents treatment A. While there may be minor differences in the trends shown by these two lines, the trends exhibited by these two lines are not significantly different.
Let’s see how to do these analyses in SPSS. The SPSS program below creates cond1 and cond2 like in the SAS program, and uses glm to perform the analyses.
if cond = 1 or cond = 2 cond1 = 1. if cond = 3 cond1 = 2. if cond = 1 cond2 = 1. if cond = 2 cond2 = 2. if cond = 3 cond2 = $sysmis. GLM sr1 to sr5 by cond1 /wsfactors = time 5. GLM sr1 to sr5 by cond2 /wsfactors = time 5.
Excerpts from the first GLM are shown below, and correspond to the SAS results.
| Tests of Within-Subjects Contrasts | |||||||
| Measure: | |||||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. | ||
| time | Linear | 59.201 | 1 | 59.201 | 14.870 | 0.000 | |
| Quadratic | 2.960 | 1 | 2.960 | 0.762 | 0.388 | ||
| Cubic | 0.001 | 1 | 0.001 | 0.001 | 0.977 | ||
| Order 4 | 1.947 | 1 | 1.947 | 1.710 | 0.198 | ||
| time * cond1 | Linear | 5.344 | 1 | 5.344 | 1.342 | 0.253 | |
| Quadratic | 6.436 | 1 | 6.436 | 1.658 | 0.205 | ||
| Cubic | 0.144 | 1 | 0.144 | 0.105 | 0.747 | ||
| Order 4 | 11.233 | 1 | 11.233 | 9.867 | 0.003 | ||
| Error(time) | Linear | 159.246 | 40 | 3.981 | |||
| Quadratic | 155.298 | 40 | 3.882 | ||||
| Cubic | 54.646 | 40 | 1.366 | ||||
| Order 4 | 45.537 | 40 | 1.138 | ||||
Excerpts from the second GLM are shown below, and they too correspond to the SAS results.
| Tests of Within-Subjects Contrasts | |||||||
| Measure: | |||||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. | ||
| time | Linear | 75.089 | 1 | 75.089 | 18.259 | 0.000 | |
| Quadratic | 13.594 | 1 | 13.594 | 3.061 | 0.092 | ||
| Cubic | 0.089 | 1 | 0.089 | 0.055 | 0.816 | ||
| Order 4 | 2.870 | 1 | 2.870 | 3.316 | 0.080 | ||
| time * cond2 | Linear | 0.289 | 1 | 0.289 | 0.070 | 0.793 | |
| Quadratic | 0.309 | 1 | 0.309 | 0.070 | 0.794 | ||
| Cubic | 2.604 | 1 | 2.604 | 1.611 | 0.216 | ||
| Order 4 | 0.270 | 1 | 0.270 | 0.312 | 0.581 | ||
| Error(time) | Linear | 106.921 | 26 | 4.112 | |||
| Quadratic | 115.454 | 26 | 4.441 | ||||
| Cubic | 42.007 | 26 | 1.616 | ||||
| Order 4 | 22.503 | 26 | 0.866 | ||||
Analysis 4: Test linear and non-linear trend
The tests from Analysis 3 allow us to assess each of the trend components. Perhaps instead we would like to assess the linear trend and the nonlinear (i.e. quadratic + cubic + order 4) trend. We could assess the non-linear trend by using the information from the prior analyses to compute the SSnon-linear by summing SSquad+SScubic+SSorder4. We could then compute the MSnonlinear by taking SSnonlinear / 3. For example, for the first analysis, the SSnonlinear would be 6.436 + .144 + 11.233 = ??? . Then the MSnonlinear would be ??? / 3. We would then divide this by the Error term. Whoops… there are different error terms for each of these effects. It is not clear what the error term would be. Here is another way you could do this, using SPSS MANOVA (note that we use SPSS MANOVA because we don’t believe this kind of analysis is possible using SAS PROC GLM or SPSS GLM).
Let’s first illustrate how you can do analysis 3 using SPSS MANOVA, as shown below.
MANOVA sr1 to sr5 by cond(1,3) /WSFACTORS = time(5) /CONTRAST(time) = POLYNOMIAL /CONTRAST(cond)=SPECIAL(1 1 1 1 1 -2 1 -1 0) /WSDESIGN=time(1) time(2) time(3) time(4) /DESIGN=cond(1) cond(2).
Here is the cond by time(order 4)interaction. The cond(1) by time(4) is the first analysis, comparing Control and Treatment A vs. Treatment B by time(order 4). You can see these results match the SAS and SPSS results. (You may note that the cond(2) by time(4) has the same SS, but a different F value. This is because this test uses the error term from all of the data, whereas the SAS and SPSS analyses use an error term based only on the data from Treatment A and Control.)
Tests involving 'TIME(4)' Within-Subject Effect. Tests of Significance for T5 using UNIQUE sums of squares Source of Variation SS DF MS F Sig of F WITHIN+RESIDUAL 45.27 39 1.16 TIME(4) .09 1 .09 .08 .786 COND(1) BY TIME(4) 11.23 1 11.23 9.68 .003 COND(2) BY TIME(4) .27 1 .27 .23 .632
Now, let’s show how you can get the linear and nonlinear tests. We want to collect together the non-linear effects of time (the second, third, and fourth orders of time). We use the partition subcommand to divide up the effects into the linear effect (i.e. the first order) and the remaining 3 df (i.e., the second, third, and fourth orders of time, the non-linear effects). Now, when we refer to time(1) we are referring to the linear effect of time, and when we refer to time(2) we are referring to the non-linear effect of time. The commands are shown below.
MANOVA sr1 to sr5 by cond(1,3) /WSFACTORS = time(5) /CONTRAST(time) = POLYNOMIAL /PARTITION(time) = (1,3) /WSDESIGN=time(1) time(2) /CONTRAST(cond)=SPECIAL(1 1 1 1 1 -2 1 -1 0) /DESIGN=cond(1) cond(2).
Below, we show the test of greatest interest, comparing Treatment B vs. Treatment A and Control by the non-linear effect of time. As we hypothesized, this result is significant. (Note that we used the MANOVA results, not the univariate results).
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. COND(1) BY TIME(2) Multivariate Tests of Significance (S = 1, M = 1/2, N = 17 1/2) Test Name Value Exact F Hypoth. DF Error DF Sig. of F Pillais .29242 5.09695 3.00 37.00 .005 Hotellings .41327 5.09695 3.00 37.00 .005 Wilks .70758 5.09695 3.00 37.00 .005 Roys .29242 Note.. F statistics are exact.
Analysis 5: Varying the covariance structure
As we discussed in Analysis #1, SAS proc glm and SPSS glm give you two sets of results, Univariate and Multivariate (MANOVA) results. These results are based on different assumption about the structure of the covariance of the scores across time. The Univariate model uses a structure called Compound Symmetry which estimates the covariance as shown below. There is a single Variance (represented by s2) for all 5 of the trials, and there is a single covariance (represented by s1) for each of the pairs of trials.
s2 s1 s2 s1 s1 s2 s1 s1 s1 s2 s1 s1 s1 s1 s2The Multivariate (MANOVA) model uses a structure called Unstructured which estimates the covariance as shown below. Each trial has its own variance (e.g., s12 is the variance of trial 1) and each pair of trials has its own covariance (e.g., s21 is the covariance of trial 1 and trial2).
s12 s21 s22 s31 s32 s32 s41 s42 s43 s42 s51 s52 s53 s54 s52
As you might imagine, these are not the only possible covariance structures, but they are the only covariance structures that are available to you if you use SAS proc glm, SPSS glm (or SPSS manova). However, SAS proc mixed or SPSS mixed allows you to select among a wide variety of covariance structures, allowing you to choose the appropriate covariance structure for your data. First, let’s illustrate how to replicate the results from analysis #1 using SAS proc mixed.
The first thing we need to do in order to use proc mixed is to get our data into the proper shape. In our prior analyses, our data was in a wide format where there was one record per subject. SAS proc mixed, however, wants the data in a long format, where there is one score per observation (yielding 5 observations per subject). We can use the program below to reshape the data from wide to long.
data replong ;
set repeat2 ;
array aib(5) ib1-ib5;
array ams(5) ms1-ms5;
array asr(5) sr1-sr5;
do time = 1 to 5;
ib = aib(time);
ms = ams(time);
sr = asr(time);
output;
end;
keep id cond time ib ms sr;
run;
proc print data=replong(obs=10);
run;
We see the output of the proc print below.
Obs id cond time ib ms sr 1 1 1 1 1415.94 64.71 8 2 1 1 2 1457.06 51.04 7 3 1 1 3 1484.38 54.40 5 4 1 1 4 1583.71 86.96 5 5 1 1 5 1603.07 90.23 6 6 2 3 1 1385.95 36.51 14 7 2 3 2 1550.62 50.29 15 8 2 3 3 1528.70 47.32 17 9 2 3 4 1541.53 43.08 17 10 2 3 5 1582.64 46.45 16
We can now use proc mixed to perform one of the Analyses from Analysis #1. This analysis assumes a compound symmetric covariance structure.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL sr = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=CS ; RUN;
If you compare these results to Analysis 1, you will see that the results match the Univariate results from SAS proc glm and SPSS glm. This makes sense, since all of these analyses are assuming the covariance is compound symmetric.
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
cond 2 39 5.70 0.0067
time 4 156 8.36 <.0001
cond*time 8 156 1.26 0.2669
SPSS mixed also wants the data to be in a long format and the SPSS 11 command vars2cases can be used to reshape the data in this way, as illustrated below.
VARSTOCASES /MAKE ib FROM ib1 ib2 ib3 ib4 ib5 /MAKE ms FROM ms1 ms2 ms3 ms4 ms5 /MAKE sr FROM sr1 sr2 sr3 sr4 sr5 /INDEX = time(5) /KEEP = cond id /NULL = KEEP.
We can then use SPSS mixed to perform this analysis as shown below.
MIXED sr by cond time /fixed = cond time cond*time /repeated = time | subject(id) covtype(cs).
As the output shows below, the results match those found with SAS proc mixed.
| Type III Tests of Fixed Effectsa | ||||
| Source | Numerator df | Denominator df | F | Sig. |
| Intercept | 1 | 39.000 | 595.704 | 0.000 |
| cond | 2 | 39.000 | 5.702 | 0.007 |
| time | 4 | 156.000 | 8.356 | 0.000 |
| cond * time | 8 | 156.000 | 1.263 | 0.267 |
| a. Dependent Variable: sr. | ||||
Now, let’s assume the covariance is Unstructured using SAS proc mixed.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL sr = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=UN R RCORR ; RUN;
The results for cond*time are similar to the Multivariate (MANOVA) results from SAS proc glm and SPSS glm. It makes sense that the results should be similar since all of these analyses are assuming the covariance is Unstructured. It makes sense that the results are not exactly the same because the SAS proc glm and SPSS glm results are from Multivariate tests, whereas the SAS proc glm results are Univariate tests, so the results would not be exactly the same.
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
cond 2 39 5.70 0.0067
time 4 39 5.30 0.0017
cond*time 8 39 2.70 0.0180
We can also assume an Unstructured covariance using SPSS mixed as shown below.
MIXED sr by cond time /fixed = cond time cond*time /repeated = time | subject(id) covtype(un).
As the results show below, the results match those found in SAS proc mixed.
Type III Tests of Fixed Effectsa Source Numerator df Denominator df F Sig. Intercept 1 39.000 595.704 0.000 cond 2 39.000 5.702 0.007 time 4 39 5.299 0.002 cond * time 8 39 2.704 0.018 a. Dependent Variable: sr.
Let’s further consider these two covariance structures. The compound symmetric covariance seems overly simplistic, and would likely be incorrect. The variance of the scores could change across trials (but the compound symmetric covariance assumes the variance is constant over trials). Also, the covariances among the trials might not all be the same, for example, the covariance may be stronger for trials that are closer together than for trials that are further apart (but the compound symmetric covariance assumes the covariances among trials are all the same).
If the compound symmetric covariance is overly simple, the unstructured covariance seems overly complex. In our example we have 5 trials, so the unstructured covariance has 5 variances and 10 covariances ( (5*4)/2 ), for a total of 15 variances and covariances being estimated. Our sample size is only 42, so we are estimating 15 variances/covariances based on just 42 subjects. We could be concerned that with such a small sample size, the variances/covariances may not be very stable, and the results would be based on these unstable estimates. Using proc mixed, we can seek a compromise, trying to find a covariance structure that strikes a balance between the simplicity of the compound symmetric covariance and the complexity of the unstructured covariance.
Let’s start by showing how we can compare 2 covariance structures. If we return to the compound symmetry results from SAS proc mixed (an5a.txt) it contains this information regarding the covariance structure.
Fit Statistics -2 Res Log Likelihood 897.0 AIC (smaller is better) 901.0 AICC (smaller is better) 901.1 BIC (smaller is better) 904.5
Likewise SPSS mixed reports these same values except the BIC values are different (but we won’t worry about that).
| Information Criteriaa | |
| -2 Restricted Log Likelihood | 897.011 |
| Akaike’s Information Criterion (AIC) | 901.011 |
| Hurvich and Tsai’s Criterion (AICC) | 901.074 |
| Bozdogan’s Criterion (CAIC) | 909.557 |
| Schwarz’s Bayesian Criterion (BIC) | 907.557 |
| The information criteria are displayed in smaller-is-better form. | |
| a. Dependent Variable: sr. | |
Likewise, the unstructured results (an5b.txt) contains this information regarding the covariance structure, as shown below from SAS proc mixed (the SPSS mixed results are omitted). (left off here)
Fit Statistics -2 Res Log Likelihood 838.3 AIC (smaller is better) 868.3 AICC (smaller is better) 871.0 BIC (smaller is better) 894.3
We can use these Fit Statistics to assess these covariance structures. As the output indicates, smaller values of Akaike’s Information Criterion (AIC) indicate better fit of the covariance structure, so the unstructured model has a better fit than the compound symmetry model but we would expect this given that it has so many more covariance parameters. Since these are nested models (one is a subset of the other) we can can test whether the additional parameters significantly improve the fit using the -2 Res Log Likelihood. We can take the differences in the Log Likelihood (897-838.3=58.7) and this is distributed as a chi-square with 15-2=13 df. This is significant even at the 0.01 level (exceeding 27.68), indicating that the additional parameters in the unstructured covariance matrix do lead to a better fit than the compound symmetric model.
Because we used the r corr options on the model statement, the covariance matrix and correlation matrix are included in the output, shown below.
Estimated R Matrix for id 1
Row Col1 Col2 Col3 Col4 Col5
1 7.5348 6.0385 6.8223 6.7802 7.1300
2 6.0385 9.9377 11.2564 9.6062 9.1410
3 6.8223 11.2564 16.5733 13.5586 12.6832
4 6.7802 9.6062 13.5586 13.4103 12.3535
5 7.1300 9.1410 12.6832 12.3535 13.4103
Estimated R Correlation Matrix for id 1
Row Col1 Col2 Col3 Col4 Col5
1 1.0000 0.6978 0.6105 0.6745 0.7093
2 0.6978 1.0000 0.8771 0.8321 0.7918
3 0.6105 0.8771 1.0000 0.9095 0.8508
4 0.6745 0.8321 0.9095 1.0000 0.9212
5 0.7093 0.7918 0.8508 0.9212 1.0000
Let’s see if we can find a more parsimonious covariance structure than UN. If we look at the correlations among the trials (shown in the second matrix) we see a little bit of a pattern that the correlations are stronger the more adjacent the scores (e.g. trial4 and trial5 is .92, where trial1 and trial5 is .71). This looks like it could be modeled with a autoregressive covariance structure. A traditional autoregressive structure should be familiar to those who have used time series analysis. The AR(1) structure is shown below. The variance is constant across trials. The covariance depends on the number of “steps” between trials, if there is one step, then it is sr and if it is two steps the covariance is sr2 and so forth.
s2 sr s2 sr2 sr s2 sr3 sr2 sr s2 sr4 sr3 sr2 sr s2
The SAS proc mixed program analyzing this data using an AR(1) structure is shown below.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL sr = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=AR(1) ; RUN;
The fit statistics are shown below.
Fit Statistics -2 Res Log Likelihood 872.8 AIC (smaller is better) 876.8 AICC (smaller is better) 876.9 BIC (smaller is better) 880.3
If you inspect the covariance matrix above (the one above the correlation matrix) and we can see that the variances on the diagonal don’t appear to be the same (7.5 9.9 16.5 13.4 and 13.4). This may indicate that a traditional AR(1) covariance structure is not best. This looks like it might be better to use an autoregressive covariance structure, with heterogeneous variances. The autoregressive with heterogeneous variances model is like the autoregressive structure except instead of a common variance down the diagonal, there are separate variances down the diagonal, illustrated below.
s12 sr s22 sr2 sr s32 sr3 sr2 sr s42 sr4 sr3 sr2 sr s52The SAS proc mixed program for this is shown below.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL sr = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=ARH(1) ; RUN;
The results are shown below:
Fit Statistics -2 Res Log Likelihood 864.6 AIC (smaller is better) 876.6 AICC (smaller is better) 877.1 BIC (smaller is better) 887.1
We can summarize the fit Statistics in the table below.
Cov Parms AIC -2RLL CS 2 901.0 897.0 UN 15 868.3 838.3 AR1 2 876.8 872.8 ARH 6 876.6 864.6
The CS and AR1 models both have 2 parameters, and we can see that the AR1 fits better (it has a higher AIC, SBC, and lower -2RLL). Previously, we tested the CS vs. UN, and found the UN to fit better. Likewise, we can compare the UN to the ARH structure by taking the difference in the -2RLL (864.6 – 838.3 = 26.3) and testing this against a Chi-Square distribution with 15-6=9 df, which is significant even at the 0.01 level (exceeding 21.66), indicating that the additional parameters in the unstructured covariance make for a significantly better fit than the ARH model. Perhaps there is a simpler covariance structure, but for this data, the unstructured covariance matrix seems to be the best fit.
Let’s try analyzing the variable ib focusing on selecting the appropriate covariance structure. Let’s start by using an un covariance structure, and show the covariance.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL ib = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=UN R RCORR; RUN;
The fit statistics and covariances are shown below.
Fit Statistics Res Log Likelihood -1137.8 Akaike's Information Criterion -1152.8 Schwarz's Bayesian Criterion -1165.8 -2 Res Log Likelihood 2275.6
Estimated R Matrix for id 1
Row Col1 Col2 Col3 Col4 Col5
1 47771 43575 42022 43310 40147
2 43575 44096 42149 43455 40317
3 42022 42149 43516 43266 40567
4 43310 43455 43266 46672 42137
5 40147 40317 40567 42137 41551
Estimated R Correlation Matrix for id 1
Row Col1 Col2 Col3 Col4 Col5
1 1.0000 0.9494 0.9217 0.9172 0.9011
2 0.9494 1.0000 0.9622 0.9579 0.9419
3 0.9217 0.9622 1.0000 0.9601 0.9540
4 0.9172 0.9579 0.9601 1.0000 0.9569
5 0.9011 0.9419 0.9540 0.9569 1.0000
Looking at the covariance matrix, it seems that a CS structure might fit this data, so let’s try a CS structure and compare it to the un.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL ib = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=CS ; RUN;
Here are the fit statistics for the cs structure.
Fit Statistics Res Log Likelihood -1149.9 Akaike's Information Criterion -1151.9 Schwarz's Bayesian Criterion -1153.6 -2 Res Log Likelihood 2299.7
Looking at the covariance matrix, it seems that a CS structure might fit this data, so let’s try a CS structure and compare it to the UN. We take the difference in the -2 Res Log Likelihoods (2299.7 – 2275.6 = 24.1) and take the difference in the number of parameters (15-2=13). This is significant at the 0.05 level (since it exceeds 22.36), indicating that the improvement in fit in the UN model is significant, although just barely significant at the 0.05 level.
Perhaps an AR(1) model would fit better without needing so many parameters.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL ib = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=AR(1) ; RUN;
Here are the fit statistics for the AR(1) model. The fit this model (-2RLL=2297.4) is not much better than the CS model (-2RLL=2299.7).
Fit Statistics Res Log Likelihood -1148.7 Akaike's Information Criterion -1150.7 Schwarz's Bayesian Criterion -1152.4 -2 Res Log Likelihood 2297.4
With the very high correlations among the scores, perhaps an ARMA (autoregressive moving average) model would fit better than the AR model. We try the ARMA model below.
PROC MIXED DATA=replong; CLASS id cond time ; MODEL ib = cond time cond*time ; REPEATED time / SUBJECT=id TYPE=ARMA(1,1) ; RUN;
The fit statistics are shown below.
Fit Statistics Res Log Likelihood -1142.3 Akaike's Information Criterion -1145.3 Schwarz's Bayesian Criterion -1147.9 -2 Res Log Likelihood 2284.7
The ARMA model fits much better than the CS model. The ARMA model has 3 parameters, compared to the CS model with 2 parameters. The difference in -2 Res Log Likelihood is (2299.7 – 2284.7 = 15) which is significant at the 0.001 level (exceeding 10.82). Comparing the ARMA model to the UN model shows that the fit of the ARMA model is not significantly worse than the UN model (2284.7-2275.6=9.1 with 15-3=12 df, p > .5). For the ib variable, the ARMA covariance structure seems to give the best fit, a better fit than the CS model, and it has fewer parameters than the UN model and does not fit significantly worse than the UN model. So, the ARMA model seems to be yield the most parsimonious fit. In this case, proc mixed offers a considerable advantage over SAS proc glm and SPSS glm, because those tools only allow the cs and un structures.