NOTE: This page was created using SPSS version 15, but the syntax should work with later versions of SPSS.
First off, let’s start with what a significant three-way interaction means. It means that there is a two-way interaction that varies across levels of a third variable. Say, for example, that a b*c interaction differs across various levels of factor a.
One way of analyzing the three-way interaction is through the use of tests of simple main-effects, e.g., the effect of one variable (or set of variables) across the levels of another variable.
We will use a small artificial dataset called threeway that has a statistically significant three-way interaction to illustrate the process. In our example data set, variables a, b and c are categorical. The techniques shown on this page can be generalized to situations in which one or more variables are continuous, but the more continuous variables that are involved in the interaction, the more complicated things get.
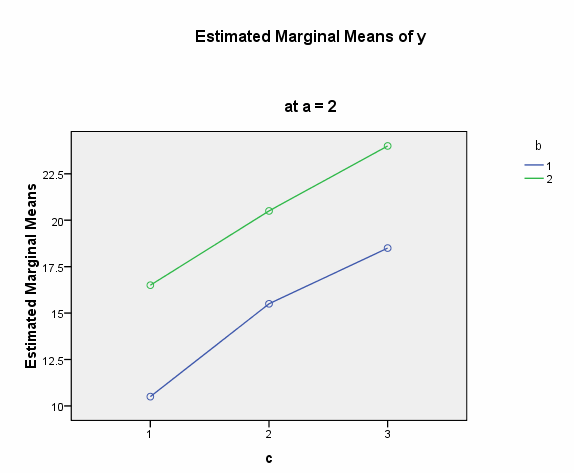
We need to select a two-way interaction to look at more closely. For the purposes of this example we will examine the b*c interaction. We can use the plot subcommand of the glm command to graph the b*c interaction for each of the two levels of a. We use the emmeans subcommands to get the numeric values that are displayed on the graphs.
get file ='D:https://stats.idre.ucla.edu/wp-content/uploads/2016/02/threeway.sav'. glm y by a b c /plot = profile(c*b*a) /emmeans=tables(a*b*c) /design = a b c a*b a*c b*c a*b*c.
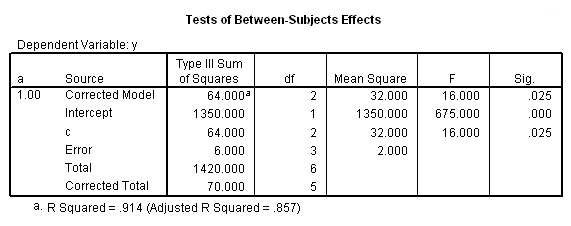
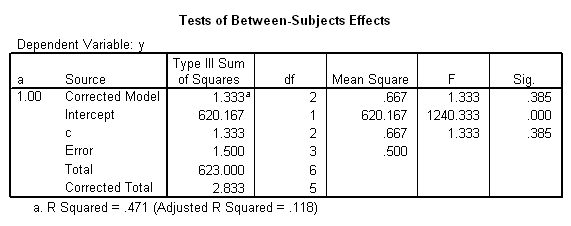
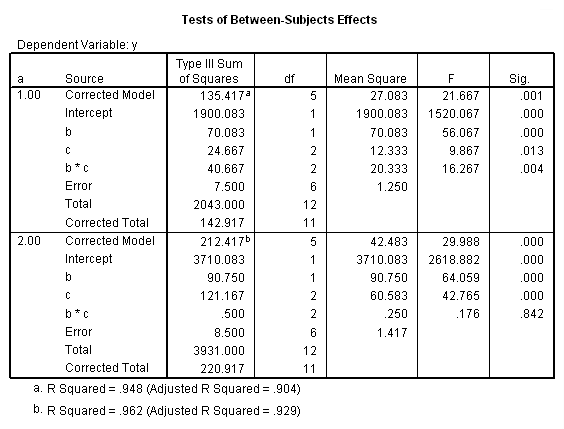
We believe from looking at the two graphs above that the three-way interaction is significant because there appears to be a "strong" two-way interaction at a = 1 and no interaction at a = 2. Now, we just have to show it statistically using tests of simple main-effects.
In SPSS, we need to conduct the tests of simple main-effects in two parts. First, we begin by running the ANOVA for both levels of a. This is easily done by sorting the data file on a, then splitting the file by a, running the ANOVA, and finally turning off the split file. To save space, we show only some of the output from the unianova command.
sort cases by a. split file by a. unianova y by b c /design = b c b*c. split file off.
Next, we need to obtain the tests of the simple main-effects for each level of a. For this example, the residual mean-square is the error term for all of the effects in the model and thus, for all of the tests of simple main-effects. There are at least three ways to conduct these tests. Perhaps the easiest way is to simply do some calculations by hand. Another way to do this is to use the lmatrix subcommand and specify the various contrasts. Once you understand how to code the contrasts on the lmatrix subcommand, this is a simple method with minimal syntax required. A third way to do this is to use OMS (Output Management System) to capture the necessary values and use aggregate to calculate the necessary values. The advantage of this method is that you can get the adjusted p-values and critical F values per family error rate; however, this requires some SPSS syntax that some people find intimidating. We have a code fragment showing the use of the lmatrix subcommand here and an example using OMS and aggregate here.
Before we start working through the hand calculations, let’s review the output from the anova above.
The syntax below is annotated to explain what each part is doing. Essentially, we are creating a new data set based on the results from the unianova command, doing some manipulations, and using the summarize command to display the results in a nice-looking table. While calculating the tests of simple main-effects, we will also calculate the critical value per family error rate. We will explain what this is and why we might want to use it later, but we are calculating it in the syntax below so that we don’t have to rerun similar syntax later. To do the necessary manipulations with the output from the unianova command, we save those results into a new data set using the Output Management System, or OMS. For more information on how to use OMS, please see our SPSS FAQ: How can I output my results to a data file in SPSS? .
* The first command calls the current data set "data", so that it can be recalled at the end.
* The second command sets up an empty data set called "tmp" where the OMS calls put data.
DATASET NAME data.
DATASET DECLARE tmp.
* OMS is used to put certain parts of the output from the command below (unianova) into a data set.
OMS
/SELECT TABLES
/IF COMMANDS=['UNIANOVA'] SUBTYPES=['Custom Univariate Tests']
/DESTINATION FORMAT=SAV NUMBERED=TableNumber_ OUTFILE='tmp'.
UNIANOVA y BY a b c
/design = a b c a*b a*c b*c a*b*c
/LMATRIX 'b*c at a=1' b*c 1 0 -1 -1 0 1 a*b*c 1 0 -1 -1 0 1 0 0 0 0 0 0;
b*c 0 1 -1 0 -1 1 a*b*c 0 1 -1 0 -1 1 0 0 0 0 0 0
/LMATRIX 'b*c at a=2' b*c 1 0 -1 -1 0 1 a*b*c 0 0 0 0 0 0 1 0 -1 -1 0 1;
b*c 0 1 -1 0 -1 1 a*b*c 0 0 0 0 0 0 0 1 -1 0 -1 1.
OMSEND.
* This is making "tmp" the active data set so that it can used in the merges (done by the aggregate command).
DATASET ACTIVATE tmp.
* The variable n_tests is added to the active data set.
AGGREGATE
/OUTFILE=* MODE=ADDVARIABLES
/PRESORTED
/BREAK=Label_
/n_tests=MAX(TableNumber_).
* The variables are added dfh and dfe to the active data set.
AGGREGATE
/OUTFILE=* MODE=ADDVARIABLES
/PRESORTED
/BREAK=TableNumber_
/dfh=FIRST(df)
/dfe=LAST(df).
* Creating a new variable Adj_Sig that will be will be the minimum of 1 and n_tests*Sig if F is not missing.
* There are still four cases in the data set.
If NOT SYSMIS(F) Adj_Sig=MIN(1,n_tests*Sig).
* Creating a new variable called "cvpfer" that will be the familywise critical value.
* 0.975 is used because we want half of alpha, which is .05, so 1-(.05/2) = .975.
COMPUTE cvpfer = idf.F(.975, dfh, dfe).
* Formatting and labeling variables.
FORMATS dfh dfe (F8.0) F cvpfer Adj_Sig (F8.4).
VARIABLE LABELS dfh 'dfh' dfe 'dfe' Adj_Sig 'Adjusted Sig.' cvpfer 'Crit. Value Per Family Error Rate'.
* Recoding the variable Subtype_ and renaming it.
IF TableNumber_=1 Subtype_='b*c at a=1'.
IF TableNumber_=2 Subtype_='b*c at a=2'.
RENAME VARIABLES Subtype_=Effect.
* This is making the summary table at the end of the output.
* The step below fills in the values for the Adj_Sig and cvpfer variables for the two contrasts.
* missing = table option in the summarize command omits lines with cells with missing values,
* so only two of the four lines in the data set are used.
* The cells = none subcommand is necessary so that the N, mean and sd are not displayed in the output.
OMS
/SELECT TABLES
/IF COMMANDS=['Summarize'] SUBTYPES=['Case Processing Summary']
/DESTINATION VIEWER=NO.
OMS
/SELECT TABLES
/IF COMMANDS=['Summarize'] SUBTYPES=['Report']
/DESTINATION VIEWER=YES.
SUMMARIZE
/TABLES=Effect F dfh dfe Adj_Sig cvpfer
/FORMAT=VALIDLIST NOCASENUM NOTOTAL
/TITLE='Tests of Simple, Simple Main Effects with Adjusted Significance Levels'
/MISSING=TABLE
/CELLS=NONE.
OMSEND.
DATASET ACTIVATE data.
DATASET CLOSE ALL.
We have omitted most of the output generated by the commands above, as this
last table is the one in which we are interested.

The F-ratio of 15.25 is the test of simple main-effects that the two-way interaction, b*c, and it is statistically significant at a = 1. The F-ratio of 0.187 is the test of simple main-effects that the two-way interaction of b*c at a = 2 is not statistically significant.
While the program above provides a p-value for the tests of simple main-effects, there are at least four different methods of determining the critical value of tests of simple main-effects. There is a method related to Dunn’s multiple comparisons, a method attributed to Marascuilo and Levin, a method called the simultaneous test procedure (very conservative and related to the Scheffé post-hoc test) and a per family error rate method.
We will demonstrate the per family error rate method, but you should look up the other methods in a good ANOVA book, like Kirk (1995), to decide which approach is best for your situation. The trick here is that we use 0.975 in the idf.F function, which is 1 minus our alpha level, .05, divided by 2, because we are doing two tests of simple main-effects.
The critical value is approximately 5.1. The first F-ratio of 15.25 is significant while the second (.1875) is not. In other words, the two-way b*c interaction is statistically significant at a = 1 but is not at a = 2.
In an ideal world we would be done now, but since we live in the “real” world, there is still more to do because we now need to try to understand the significant two-way interaction at a = 1; first for b = 1 and then for b = 2. We will do this by creating a filter variable (which we called filter1 for a=1 and b=1 and filter2 for a=1 and b=2) and using it to look at the differences in c at b = 1 when a = 1.
/* look at differences in c at b==1 when a==1 */ compute filter1 = 0. if b=1 and a=1 filter1 = 1. filter by filter1. unianova y by c. filter off.
/* look at differences in c at b==2 when a==1 */compute filter2 = 0. if b=2 and a=1 filter2 = 1. filter by filter2. unianova y by c. filter off.
To get the tests of simple main-effects for c when b = 1 and b = 2 (assuming a = 1, because that was the only level of a for which the b*c interaction was statistically significant), we need to do some more programming.
DATASET NAME data. DATASET DECLARE tmp. OMS /SELECT TABLES /IF COMMANDS=['UNIANOVA'] SUBTYPES=['Custom Univariate Tests'] /DESTINATION FORMAT=SAV NUMBERED=TableNumber_ OUTFILE='tmp'. UNIANOVA y BY a b c /LMATRIX 'c at a=1 & b=1' c 1 0 -1 a*c 1 0 -1 0 0 0 b*c 1 0 -1 0 0 0 a*b*c 1 0 -1 0 0 0 0 0 0 0 0 0; c 0 1 -1 a*c 0 1 -1 0 0 0 b*c 0 1 -1 0 0 0 a*b*c 0 1 -1 0 0 0 0 0 0 0 0 0 /LMATRIX 'c at a=1 & b=2' c 1 0 -1 a*c 1 0 -1 0 0 0 b*c 0 0 0 1 0 -1 a*b*c 0 0 0 1 0 -1 0 0 0 0 0 0; c 0 1 -1 a*c 0 1 -1 0 0 0 b*c 0 0 0 0 1 -1 a*b*c 0 0 0 0 1 -1 0 0 0 0 0 0. OMSEND. DATASET ACTIVATE tmp. AGGREGATE /OUTFILE=* MODE=ADDVARIABLES /PRESORTED /BREAK=Label_ /n_tests=MAX(TableNumber_). AGGREGATE /OUTFILE=* MODE=ADDVARIABLES /PRESORTED /BREAK=TableNumber_ /dfh=FIRST(df) /dfe=LAST(df). If NOT SYSMIS(F) Adj_Sig=MIN(1,n_tests*Sig). FORMATS dfh dfe (F8.0) Adj_Sig (F8.3). VARIABLE LABELS dfh 'dfh' dfe 'dfe' Adj_Sig 'Adjusted Sig.'. IF TableNumber_=1 Subtype_='c at a=1 & b=1'. IF TableNumber_=2 Subtype_='c at a=1 & b=2'. RENAME VARIABLES Subtype_=Effect. OMS /SELECT TABLES /IF COMMANDS=['Summarize'] SUBTYPES=['Case Processing Summary'] /DESTINATION VIEWER=NO. OMS /SELECT TABLES /IF COMMANDS=['Summarize'] SUBTYPES=['Report'] /DESTINATION VIEWER=YES. SUMMARIZE /TABLES=Effect F dfh dfe Adj_Sig /FORMAT=VALIDLIST NOCASENUM NOTOTAL /TITLE='Tests of Simple, Simple Main Effects with Adjusted Significance Levels' /MISSING=TABLE /CELLS=NONE. OMSEND. DATASET ACTIVATE data. DATASET CLOSE ALL.
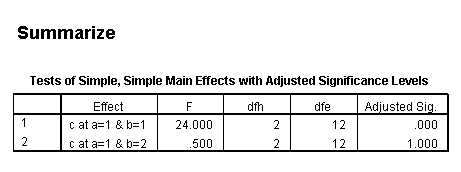
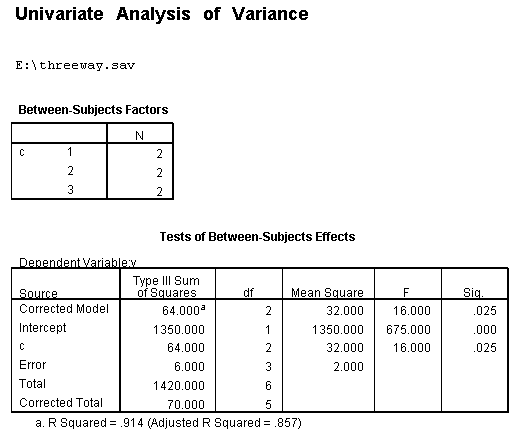
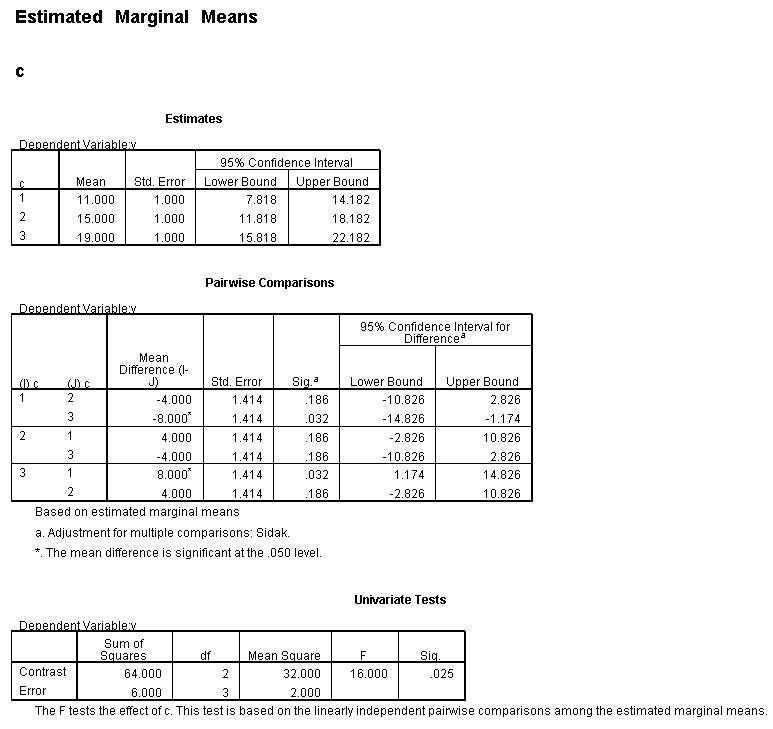
Only the test of simple main-effects of c at b = 1 was significant. But we're not done yet, since there are three levels of c, we don't know where this significant effect lies. We need to test the pairwise comparisons among the three means. We will do this using the Sidak correction for multiple tests.
filter by filter1. unianova y by c /emmeans=tables(c) compare(c) adj(sidak) . filter off.
As shown above, only one of the comparisons is statistically significant. However, the Sidak correction can be conservative. If we had used a different correction, say the Tukey HSD, all three comparisons would be statistically significant. We should note that the error term used in these comparisons is not the error term from the original three-way ANOVA. We would need to use syntax similar to that shown above to save that error term to a new data set and then use it in the comparisons (as shown on https://stats.idre.ucla.edu/stat/stata/faq/threeway.htm ). We might want to use the error term from the original three-way ANOVA because we are going post-hoc tests of that analysis. Hopefully, we now have a much better understanding of the three-way a*b*c interaction.
Please note that the process of investigating the three-way interactions would have be similar if we had chosen a different two-way interaction back at the beginning.
Summary of Steps
1) Run full model with three-way interaction.
1a) Capture SS and df residual.
2) Run two-way interaction at each level of third variable.
2a) Capture SS and df for interactions.
2b) Compute F-ratios for tests of simple main-effects.
3) Run one-way model at each level of second variable.
3a) Capture SS and df for main effects.
3b) Compute F-ratios for tests of simple main-effects.
4) Run pairwise or other post-hoc comparisons if necessary.
References
Kirk, Roger E. (1995) Experimental Design: Procedures for the Behavioral Sciences, Third Edition. Monterey, California: Brooks/Cole Publishing.