Sometimes your research hypothesis may predict that the size of a regression coefficient may vary across groups. For example, you might believe that the regression coefficient of height predicting weight would differ across three age groups (young, middle age, senior citizen). Below, we have a data file with 10 fictional young people, 10 fictional middle age people, and 10 fictional senior citizens, along with their height in inches and their weight in pounds. The variable age indicates the age group and is coded 1 for young people, 2 for middle aged, and 3 for senior citizens. Below we show two ways that you can get this data file into SPSS. One way is to cut and paste the following code into an SPSS syntax window and run it.
data list list / id age height weight. begin data. 1 1 56 140 2 1 60 155 3 1 64 143 4 1 68 161 5 1 72 139 6 1 54 159 7 1 62 138 8 1 65 121 9 1 65 161 10 1 70 145 11 2 56 117 12 2 60 125 13 2 64 133 14 2 68 141 15 2 72 149 16 2 54 109 17 2 62 128 18 2 65 131 19 2 65 131 20 2 70 145 21 3 64 211 22 3 68 223 23 3 72 235 24 3 76 247 25 3 80 259 26 3 62 201 27 3 69 228 28 3 74 245 29 3 75 241 30 3 82 269 end data. execute.
Another way is to click on https://stats.idre.ucla.edu/wp-content/uploads/2016/02/compreg3.sav and then use the get file command (insert the proper drive letter if you did not place the file in your current directory):
get file 'c:https://stats.idre.ucla.edu/wp-content/uploads/2016/02/compreg3.sav'.
After first sorting by age, we analyze the data for each age group separately using the regression command. In order to use just the data for a specific age group, we need to use a filter to "filter out" the other data. Remember that when you have completed the analysis, you need to turn the filter off.
sort cases by age. split file by age. regression /dep weight /method=enter height. split file off. exe.
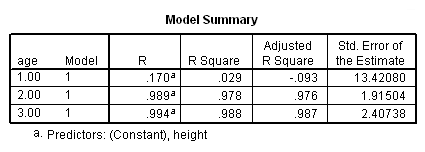
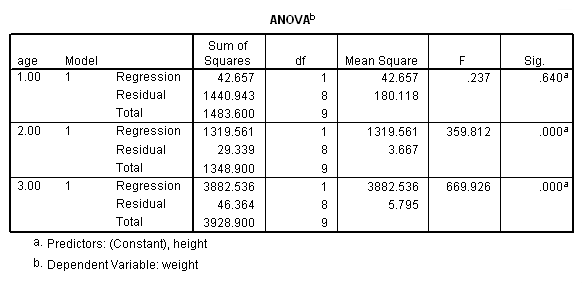
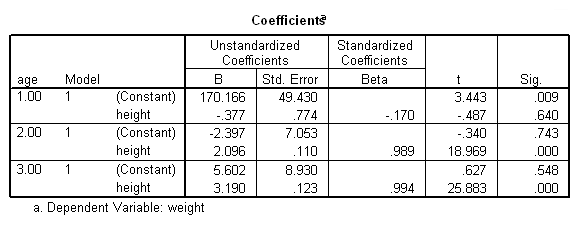
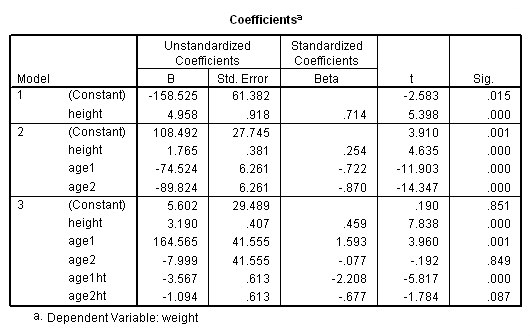
The parameter estimates (coefficients) for the young, middle age, and senior citizens are shown below, and the results do seem to suggest that height is a stronger predictor of weight for seniors (3.18) than for the middle aged (2.09). The results also seem to suggest that height does not predict weight as strongly for the young (-.37) as for the middle aged and seniors. However, we would need to perform specific significance tests to be able to make claims about the differences among these regression coefficients.
< some output omitted to save space >
We can compare the regression coefficients among these three age groups to test the null hypothesis
Ho: B1 = B2 = B3
where B1 is the regression for the young, B2 is the regression for the middle aged, and B3 is the regression for senior citizens. To do this analysis, we first make a dummy variable called age1 that is coded 1 if young (age=1), 0 otherwise, and age2 that is coded 1 if middle aged (age=2), 0 otherwise. We also create age1ht that is age1 times height, and age2ht that is age2 times height.
compute age1 = 0. compute age2 = 0. if age = 1 age1 = 1. if age = 2 age2 = 1. compute age1ht = age1*height. compute age2ht = age2*height. execute.
We can now use age1 age2 height, age1ht and age2ht as predictors in the regression equation in the regress command below. The regression command will be followed by
/method = test(age1 age2)and
/method = test(age1ht age2ht)
The first one provides a 2 degree of freedom to determine if, taken together, the variable age is statistically significant. We have included this for the sake of completeness, because this is a standard part of the analysis. The second subcommand tests the null hypothesis
Ho: B1 = B2 = B3
This test will also have 2 degrees of freedom because it compares among three regression coefficients.
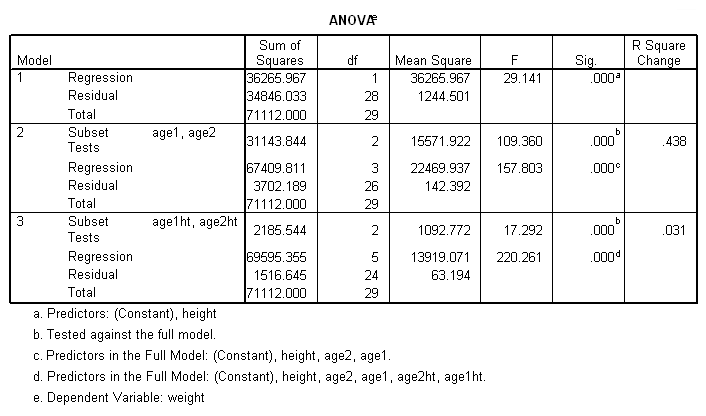
regression /dep weight /method = enter height /method=test(age1 age2) /method = test(age1ht age2ht).
< some output omitted to save space >
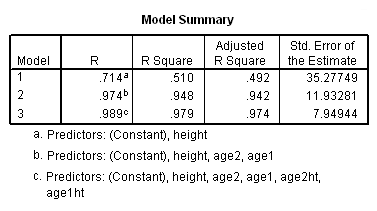
The analysis below shows that the null hypothesis
Ho: B1 = B2 = B3
can be rejected (F=17.292, p = 0.000). This means that the regression coefficients between height and weight do indeed significantly differ across the three age groups (young, middle age, senior citizen).