Version info: Code for this page was tested in IBM SPSS 20.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics and potential follow-up analyses.
Examples of ordered logistic regression
Example 1: A marketing research firm wants to investigate what factors influence the size of soda (small, medium, large or extra large) that people order at a fast-food chain. These factors may include what type of sandwich is ordered (burger or chicken), whether or not fries are also ordered, and age of the consumer. While the outcome variable, size of soda, is obviously ordered, the difference between the various sizes is not consistent. The difference between small and medium is 10 ounces, between medium and large 8, and between large and extra large 12.
Example 2: A researcher is interested in what factors influence medaling in Olympic swimming. Relevant predictors include at training hours, diet, age, and popularity of swimming in the athlete’s home country. The researcher believes that the distance between gold and silver is larger than the distance between silver and bronze.
Example 3: A study looks at factors that influence the decision of whether to apply to graduate school. College juniors are asked if they are unlikely, somewhat likely, or very likely to apply to graduate school. Hence, our outcome variable has three categories. Data on parental educational status, whether the undergraduate institution is public or private, and current GPA is also collected. The researchers have reason to believe that the “distances” between these three points are not equal. For example, the “distance” between “unlikely” and “somewhat likely” may be shorter than the distance between “somewhat likely” and “very likely”.
Description of the data
For our data analysis below, we are going to expand on Example 3 about applying to graduate school. We have simulated some data for this example and it can be obtained from here: ologit.sav This hypothetical data set has a three-level variable called apply (coded 0, 1, 2), that we will use as our outcome variable. We also have three variables that we will use as predictors: pared, which is a 0/1 variable indicating whether at least one parent has a graduate degree; public, which is a 0/1 variable where 1 indicates that the undergraduate institution is public and 0 private, and gpa, which is the student’s grade point average.
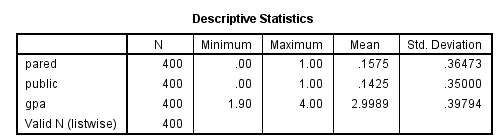
Let’s start with the descriptive statistics of these variables.
get file "D:\data\ologit.sav". freq var = apply pared public.descriptives var = gpa.
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable while others have either fallen out of favor or have limitations.
- Ordered logistic regression: the focus of this page.
- OLS regression: This analysis is problematic because the assumptions of OLS are violated when it is used with a non-interval outcome variable.
- ANOVA: If you use only one continuous predictor, you could “flip” the model around so that, say, gpa was the outcome variable and apply was the predictor variable. Then you could run a one-way ANOVA. This isn’t a bad thing to do if you only have one predictor variable (from the logistic model), and it is continuous.
- Multinomial logistic regression: This is similar to doing ordered logistic regression, except that it is assumed that there is no order to the categories of the outcome variable (i.e., the categories are nominal). The downside of this approach is that the information contained in the ordering is lost.
- Ordered probit regression: This is very, very similar to running an ordered logistic regression. The main difference is in the interpretation of the coefficients.
Ordered logistic regression
Before we run our ordinal logistic model, we will see if any cells are empty or extremely small. If any are, we may have difficulty running our model. There are two ways in SPSS that we can do this. The first way is to make simple crosstabs. The second way is to use the cellinfo option on the /print subcommand. You should use the cellinfo option only with categorical predictor variables; the table will be long and difficult to interpret if you include continuous predictors.
crosstabs /tables = apply by pared /tables = apply by public.plum apply with pared public /link = logit /print = cellinfo.
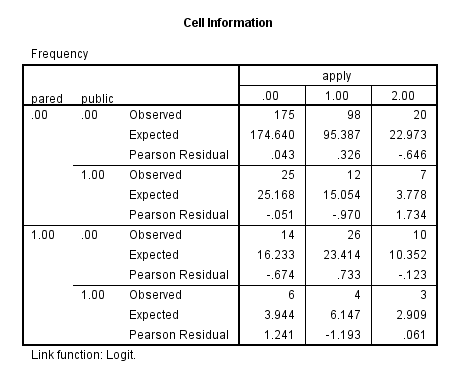
None of the cells is too small or empty (has no cases), so we will run our model. In the syntax below, we have included the link = logit subcommand, even though it is the default, just to remind ourselves that we are using the logit link function. Also note that if you do not include the print subcommand, only the Case Processing Summary table is provided in the output.
plum apply with pared public gpa /link = logit /print = parameter summary.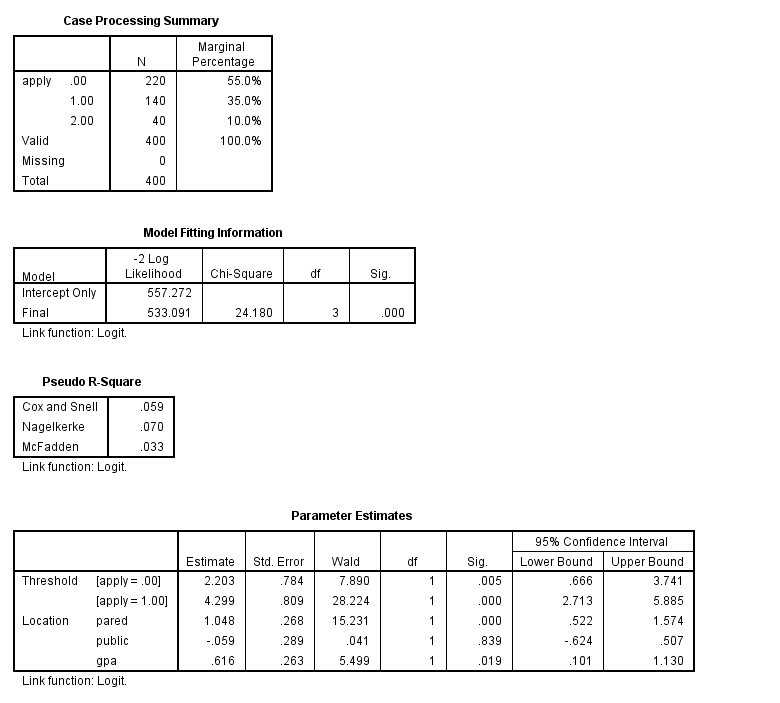
In the Case Processing Summary table, we see the number and percentage of cases in each level of our response variable. These numbers look fine, but we would be concerned if one level had very few cases in it. We also see that all 400 observations in our data set were used in the analysis. Fewer observations would have been used if any of our variables had missing values. By default, SPSS does a listwise deletion of cases with missing values. Next we see the Model Fitting Information table, which gives the -2 log likelihood for the intercept-only and final models. The -2 log likelihood can be used in comparisons of nested models, but we won’t show an example of that here.
In the Parameter Estimates table we see the coefficients, their standard errors, the Wald test and associated p-values (Sig.), and the 95% confidence interval of the coefficients. Both pared and gpa are statistically significant; public is not.& So for pared, we would say that for a one unit increase in pared (i.e., going from 0 to 1), we expect a 1.05 increase in the ordered log odds of being in a higher level of apply, given all of the other variables in the model are held constant. For gpa, we would say that for a one unit increase in gpa, we would expect a 0.62 increase in the log odds of being in a higher level of apply, given that all of the other variables in the model are held constant. The thresholds are shown at the top of the parameter estimates output, and they indicate where the latent variable is cut to make the three groups that we observe in our data. Note that this latent variable is continuous. In general, these are not used in the interpretation of the results. Some statistical packages call the thresholds “cutpoints” (thresholds and cutpoints are the same thing); other packages, such as SAS report intercepts, which are the negative of the thresholds. In this example, the intercepts would be -2.203 and -4.299. For further information, please see the Stata FAQ: How can I convert Stata’s parameterization of ordered probit and logistic models to one in which a constant is estimated?
As of version 15 of SPSS, you cannot directly obtain the proportional odds ratios from SPSS. You can either use the SPSS Output Management System (OMS) to capture the parameter estimates and exponentiate them, or you can calculate them by hand. Please see Ordinal Regression by Marija J. Norusis for examples of how to do this. The commands for using OMS and calculating the proportional odds ratios is shown below. For more information on how to use OMS, please see our SPSS FAQ: How can I output my results to a data file in SPSS? Please note that the single quotes in the square brackets are important, and you will get an error message if they are omitted or unbalanced.
oms select tables /destination format = sav outfile = "D:\ologit_results.sav" /if commands = ['plum'] subtypes = ['Parameter Estimates']. plum apply with pared public gpa /link = logit /print = parameter. omsend. get file "D:\ologit_results.sav". rename variables Var2 = Predictor_Variables. * the next command deletes the thresholds from the data set. select if Var1 = "Location". exe. * the command below removes unnessary variables from the data set. * transformations cannot be pending for the command below to work, so * the exe. * above is necessary. delete variables Command_ Subtype_ Label_ Var1. compute expb = exp(Estimate). compute Lower_95_CI = exp(LowerBound). compute Upper_95_CI = exp(UpperBound). execute.
In the column expb we see the results presented as proportional odds ratios (the coefficient exponentiated). We have also calculated the lower and upper 95% confidence interval. We would interpret these pretty much as we would odds ratios from a binary logistic regression. For pared, we would say that for a one unit increase in pared, i.e., going from 0 to 1, the odds of high apply versus the combined middle and low categories are 2.85 greater, given that all of the other variables in the model are held constant. Likewise, the odds of the combined middle and high categories versus low apply is 2.85 times greater, given that all of the other variables in the model are held constant. For a one unit increase in gpa, the odds of the low and middle categories of apply versus the high category of apply are 1.85 times greater, given that the other variables in the model are held constant. Because of the proportional odds assumption (see below for more explanation), the same increase, 1.85 times, is found between low apply and the combined categories of middle and high apply.
One of the assumptions underlying ordered logistic (and ordered probit) regression is that the relationship between each pair of outcome groups is the same. In other words, ordered logistic regression assumes that the coefficients that describe the relationship between, say, the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories, etc. This is called the proportional odds assumption or the parallel regression assumption. Because the relationship between all pairs of groups is the same, there is only one set of coefficients (only one model). If this was not the case, we would need different models to describe the relationship between each pair of outcome groups. We need to test the proportional odds assumption, and we can use the tparallel option on the print subcommand. The null hypothesis of this chi-square test is that there is no difference in the coefficients between models, so we hope to get a non-significant result.
plum apply with pared public gpa /link = logit /print = tparallel.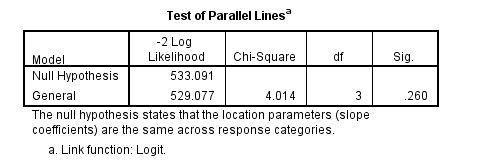
The above test indicates that we have not violated the proportional odds assumption. If the proportional odds assumption was violated, we may want to go with multinomial logistic regression.
We we use these formulae to calculate the predicted probabilities for each level of the outcome, apply. Predicted probabilities are usually easier to understand than the coefficients or the odds ratios.
$$P(Y = 2) = \left(\frac{1}{1 + e^{-(a_{2}+b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3})}}\right)$$ $$P(Y = 1) = \left(\frac{1}{1 + e^{-(a_{1}+b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3})}}\right) – P(Y = 2)$$ $$P(Y = 0) = 1 – P(Y = 1) – P(Y = 2)$$
We will calculate the predicted probabilities using SPSS’ Matrix language. We will use pared as an example with a categorical predictor. Here we will see how the probabilities of membership to each category of apply change as we vary pared and hold the other variable at their means. As you can see, the predicted probability of being in the lowest category of apply is 0.59 if neither parent has a graduate level education and 0.34 otherwise. For the middle category of apply, the predicted probabilities are 0.33 and 0.47, and for the highest category of apply, 0.078 and 0.196 (annotations were added to the output for clarity). Hence, if neither of a respondent’s parents have a graduate level education, the predicted probability of applying to graduate school decreases. Note that the intercepts are the negatives of the thresholds. For a more detailed explanation of how to interpret the predicted probabilities and its relation to the odds ratio, please refer to FAQ: How do I interpret the coefficients in an ordinal logistic regression?
Matrix.
* intercept1 intercept2 pared public gpa.
* these coefficients are taken from the output.
compute b = {-2.203 ; -4.299 ; 1.048 ; -.059 ; .616}.
* overall design matrix including means of public and gpa.
compute x = {{0, 1, 0; 0, 1, 1}, make(2, 1, .1425), make(2, 1, 2.998925)}.
compute p3 = 1/(1 + exp(-x * b)).
* overall design matrix including means of public and gpa.
compute x = {{1, 0, 0; 1, 0, 1}, make(2, 1, .1425), make(2, 1, 2.998925)}.
compute p2 = (1/(1 + exp(-x * b))) - p3.
compute p1 = make(NROW(p2), 1, 1) - p2 - p3.
compute p = {p1, p2, p3}.
print p / FORMAT = F5.4 / title = "Predicted Probabilities for Outcomes 0 1 2 for pared 0 1 at means".
End Matrix.
Run MATRIX procedure:
Predicted Probabilities for Outcomes 0 1 2 for pared 0 1 at means
(apply=0) (apply=1) (apply=2)
(pared=0) .5900 .3313 .0787
(pared=1) .3354 .4687 .1959
------ END MATRIX -----
Below, we see the predicted probabilities for gpa at 2, 3 and 4. You can see that the predicted probability increases for both the middle and highest categories of apply as gpa increases (annotations were added to the output for clarity). For a more detailed explanation of how to interpret the predicted probabilities and its relation to the odds ratio, please refer to FAQ: How do I interpret the coefficients in an ordinal logistic regression?
Matrix.
* intercept1 intercept2 pared public gpa.
* these coefficients are taken from the output.
compute b = {-2.203 ; -4.299 ; 1.048 ; -.059 ; .616}.
* overall design matrix including means of pared and public.
compute x = {make(3, 1, 0), make(3, 1, 1), make(3, 1, .1575), make(3, 1, .1425), {2; 3; 4}}.
compute p3 = 1/(1 + exp(-x * b)).
* overall design matrix including means of pared and public.
compute x = {make(3, 1, 1), make(3, 1, 0), make(3, 1, .1575), make(3, 1, .1425), {2; 3; 4}}.
compute p2 = (1/(1 + exp(-x * b))) - p3.
compute p1 = make(NROW(p2), 1, 1) - p2 - p3.
compute p = {p1, p2, p3}.
print p / FORMAT = F5.4 / title = "Predicted Probabilities for Outcomes 0 1 2 for gpa 2 3 4 at means".
End Matrix.
Run MATRIX procedure:
Predicted Probabilities for Outcomes 0 1 2 for gpa 2 3 4 at means
(apply=0) (apply=1) (apply=2)
(gpa=2) .6930 .2553 .0516
(gpa=3) .5494 .3590 .0916
(gpa=4) .3971 .4456 .1573
------ END MATRIX -----
Things to consider
- Perfect prediction: Perfect prediction means that one value of a predictor variable is associated with only one value of the response variable. If this happens, Stata will usually issue a note at the top of the output and will drop the cases so that the model can run.
- Sample size: Both ordered logistic and ordered probit, using maximum likelihood estimates, require sufficient sample size. How big is big is a topic of some debate, but they almost always require more cases than OLS regression.
- Empty cells or small cells: You should check for empty or small cells by doing a crosstab between categorical predictors and the outcome variable. If a cell has very few cases, the model may become unstable or it might not run at all.
- Pseudo-R-squared: There is no exact analog of the R-squared found in OLS. There are many versions of pseudo-R-squares. Please see Long and Freese 2005 for more details and explanations of various pseudo-R-squares.
- Diagnostics: Doing diagnostics for non-linear models is difficult, and ordered logit/probit models are even more difficult than binary models.
References
- Agresti, A. (1996) An Introduction to Categorical Data Analysis. New York: John Wiley & Sons, Inc
- Agresti, A. (2002) Categorical Data Analysis, Second Edition. Hoboken, New Jersey: John Wiley & Sons, Inc.
- Liao, T. F. (1994) Interpreting Probability Models: Logit, Probit, and Other Generalized Linear Models. Thousand Oaks, CA: Sage Publications, Inc.
- Powers, D. and Xie, Yu. Statistical Methods for Categorical Data Analysis. Bingley, UK: Emerald Group Publishing Limited.
