NOTE: Zero-inflated negative binomial regression using proc countreg is only available in SAS version 9.2 or higher.
This page shows an example of zero-inflated negative binomial regression analysis with footnotes explaining the output in SAS. We have data on 250 groups that went to a park for a weekend, fish.sas7bdat. Each group was questioned about how many fish they caught (count), how many children were in the group (child), how many people were in the group (persons), and whether or not they brought a camper to the park (camper). We explore the relationship of count with child, camper and persons.
As assumed for a negative binomial model, our response variable is a count variable and the variance of the response variable is greater than the mean of the response variable. Sometimes when analyzing a response variable that is a count variable, the number of zeroes may seem excessive. In a dataset in which the response variable is a count, the number of zeroes may seem excessive. With the example dataset in mind, consider the processes that could lead to a response variable value of zero. A group may have spent the entire weekend fishing, but failed to catch a fish. Another group may have not done any fishing over the weekend and, not surprisingly, caught zero fish. The first group could have caught one or more fish, but did not. The second group was certain to catch zero fish. The second group will be referred to from this point forward as a “certain zero”. Thus, the number of zeroes may be inflated and the number of groups catching zero fish cannot be explained in the same manner as the groups that caught more than zero fish.
A standard negative binomial model would not distinguish between the two processes causing an excessive number of zeroes, but a zero-inflated model allows for and accommodates this complication. When analyzing a dataset with an excessive number of outcome zeros and two possible processes that arrive at a zero outcome, a zero-inflated model should be considered. We can look at a histogram of the response variable to try to gauge if the number of zeros is excessive. (If two processes generated the zeroes in the response variable but there is not an excessive number of zeroes, a zero-inflated model may or may not be used.)
data fish; set "D:\data\fish"; run; proc means data = fish mean std min max var; var count child persons; run; The MEANS Procedure Variable Mean Std Dev Minimum Maximum Variance ---------------------------------------------------------------------------------------- count 3.2960000 11.6350281 0 149.0000000 135.3738795 child 0.6840000 0.8503153 0 3.0000000 0.7230361 persons 2.5280000 1.1127303 1.0000000 4.0000000 1.2381687 ---------------------------------------------------------------------------------------- proc univariate data = fish noprint; histogram count / midpoints = 0 to 50 by 1 vscale = count ; run;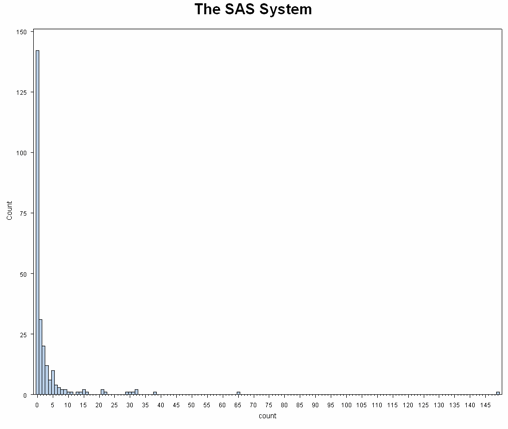
The zero-inflated negative binomial regression generates two separate models and then combines them. First, a logit model is generated for the “certain zero” cases described above, predicting whether or not a student would be in this group. Then, a negative binomial model is generated to predict the counts for those students who are not certain zeros. Finally, the two models are combined. In SAS, the proc countreg procedure that can easily run a zero-inflated negative binomial regression.
When running a zero-inflated negative binomial model in proc genmod, you must specify both models: first the count model on the model statement, then the model predicting the certain zeros on the zeromodel statement. In this example, we are predicting count with child and camper and predicting the certain zeros with persons. The code for this model and its output can be seen below.
proc countreg data = fish method = qn; model count = child camper / dist= zinegbin; zeromodel count ~ persons; run;The COUNTREG Procedure Model Fit Summary Dependent Variable count Number of Observations 250 Data Set WORK.FISH Model ZINB ZI Link Function Logistic Log Likelihood -432.89091 Maximum Absolute Gradient 7.13505E-8 Number of Iterations 28 Optimization Method Dual Quasi-Newton AIC 877.78181 SBC 898.91058 Algorithm converged. Parameter Estimates Standard Approx Parameter DF Estimate Error t Value Pr > |t| Intercept 1 1.371048 0.256114 5.35 <.0001 child 1 -1.515255 0.195591 -7.75 <.0001 camper 1 0.879051 0.269274 3.26 0.0011 Inf_Intercept 1 1.603106 0.836493 1.92 0.0553 Inf_persons 1 -1.666566 0.679265 -2.45 0.0141 _Alpha 1 2.678759 0.471328 5.68 <.0001
Model Fit
Model Fit Summary Dependent Variable count Number of Observations 250 Data Set WORK.FISH Model ZINB ZI Link Functiona Logistic Log Likelihoodb -432.89091 Maximum Absolute Gradient 7.13505E-8 Number of Iterationsc 28 Optimization Method Dual Quasi-Newton AICd 877.78181 SBCe 898.91058
a. ZI Link Function – This indicates the type of model that will be used to predict the excessive zeroes. In this example, a logistic model will be used. This is the default for zero-inflated negative binomial models in proc countreg.
b. Log Likelihood – This is the log likelihood of the fitted full model. It is calculated from the probability of the data given the model’s parameter estimates. The parameter estimates that are reported in the output are those that maximize the log likelihood of the model.
c. Number of Iterations – The fitting of this model is an iterative procedure. With each iteration of the model, the parameters are updated and the log-likelihood is calculated. This process continues until the log-likelihood is no longer improved and has been maximized. The number of iterations required by SAS to reach this point are reported here.
d. AIC – This is the Akaike Information Criterion. It is calculated as AIC = -2 Log Likelihood + 2(s), where s is the total number of predictors in the model. In this example, s = 6 and we can see AIC = -2* -432.89091 + 2*6 = 877.78181. AIC is used for the comparison of models from different samples or nonnested models. It penalizes for the number of predictors in the model. Ultimately, the model with the smallest AIC is considered the best.
e. SBC – This is Schwartz’s Bayesian information criterion. Like the AIC, it is based on the log likelihood and penalizes for the number of predictors in the model. The smallest SBC is most desirable.
Parameter Estimates
Parameter Estimates
Standard Approx
Parameterf DF Estimateg Errorh t Valuei Pr > |t|j
Intercept 1 1.371048 0.256114 5.35 <.0001
child 1 -1.515255 0.195591 -7.75 <.0001
camper 1 0.879051 0.269274 3.26 0.0011
Inf_Intercept 1 1.603106 0.836493 1.92 0.0553
Inf_persons 1 -1.666566 0.679265 -2.45 0.0141
_Alphak 1 2.678759 0.471328 5.68 <.0001
f. Parameter – These refer to the independent variables in the model as well as intercepts (a.k.a. constants) and, in the case of negative binomial regression, a dispersion parameter. The parameter names that begin Inf_ are the parameters from the inflation model. The dispersion parameter is _Alpha.
g. Estimate – These are the regression coefficients. The coefficients for Intercept, child, and camper are interpreted as you would interpret coefficients from a standard negative binomial model: the expected number of fish caught changes by a factor of exp(Estimate) for each unit increase in the corresponding predictor.
Predicting Number of Fish Caught for the Non-“Certain Zero” Groups
child – If a group were to increase its child count by one, the expected number of fish caught would decrease by a factor of exp(-1.515255) = 0.2197521 while holding all other variables in the model constant. Thus, the more children in a group, the fewer caught fish are predicted.
camper – The expected number of fish caught in a weekend for a group with a camper is exp(0.879051) = 2.408613 times the expected number of fish caught in a weekend for a group without a camper while holding all other variables in the model constant. Thus, if a group with a camper and a group without a camper are not certain zeros and have identical numbers of children, the expected number fish caught for the group with a camper is 2.408613 times the expected number of fish caught by the group without a camper.
Intercept – If all of the predictor variables in the model are evaluated at zero, the predicted number of fish caught would be calculated as exp(Intercept) = exp(1.371048). For groups without a camper or children (the variables camper and child evaluated at zero), the predicted number of fish caught would be 3.939477.
Predicting “Certain Zero” Groups
Inf_persons- If a group were to increase its persons value by one, the odds that it would be a “Certain Zero” would decrease by a factor of exp(-1.666566) = 0.1888946. In other words, the more people in a group, the less likely the group is a certain zero.
Inf_Intercept – If all of the predictor variables in the inflation model are evaluated at zero, the odds of being a “Certain Zero” is exp(1.603106) = 4.96844. This means that the predicted odds of a group with zero persons is 4.96844 (though remember that evaluating persons at zero is out of the range of plausible values–every group must have at least one person).
h. Standard Error – These are the standard errors of the individual regression coefficients for the two models. They are used in both the calculation of the t test statistic, superscript i.
i. t Value – This is the test statistic used to test against a null hypothesis that the Estimate is equal to zero. The t Value is the ratio of the Estimate to the Standard Error of the given predictor. The value follows a t-distribution with (# of observations – # of parameters) = (250 – 6) = 244 degrees of freedom.
j. Approx Pr > |t| – This is the approximate probability of the t test statistic (or a more extreme test statistic) would be observed under the null hypothesis. The null hypothesis is that the coefficient is zero, given that the rest of the predictors are in the model. For a given alpha level, P>|t| determines whether or not the null hypothesis can be rejected. If P>|t| is less than alpha, then the null hypothesis can be rejected and the parameter estimate is considered significant at that alpha level.
Predicting Number of Fish Caught for the Non-“Certain Zero” Groups
child – The t test statistic for the predictor child is (-1.515255/ 0.195591) = -7.75 with an associated p-value of <.0001. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for child has been found to be statistically different from zero given the other variables are in the model.
camper –The t test statistic for the predictor camper is (0.879051/0.269274) = 3.26 with an associated p-value of 0.0011. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for camper has been found to be statistically different from zero given the other variables are in the model.
Intercept – The t test statistic for the intercept, Intercept, is (1.371048/0.256114) = 5.35 with an associated p-value of < 0.001. If we set our alpha level at 0.05, we would reject the null hypothesis and conclude that Intercept has been found to be statistically different from zero given the other variables are in the model and evaluated at zero.
Predicting “Certain Zero” Groups
Inf_persons- The t test statistic for the predictor Inf_persons is (-1.666566/0.679265) = -2.45 with an associated p-value of 0.0141. If we again set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for Inf_persons has been found to be statistically different from zero given the other variables are in the model.
Inf_Intercept -The t test statistic for the intercept, Inf_Intercept, is (1.603106/0.836493) = 1.92 with an associated p-value of 0.0553. With an alpha level of 0.05, we would fail to reject the null hypothesis and conclude that Inf_Intercept has not been found to be statistically different from zero given the other variables are in the model.
k. _Alpha – This is the dispersion parameter of the count model. If the dispersion parameter is zero, then log(dispersion parameter) = -infinity. If this is true, then a Poisson model would be appropriate. Based on the t value of 5.68 and the associated p-value of <.0001, we can reject the null hypothesis that _Alpha is equal to zero. Thus, a Poisson model would not be appropriate and we are justified in using a negative binomial model.
