After running a logistic model with multiple predictors or an interaction, you may wish to be able to see predicted values with confidence intervals for different combinations of predictors. This can easily be done with the adjust command in Stata (see Stata FAQ: How do I use adjust in probit or logit?). This page will demonstrate how to achieve this in SAS by combining the outmodel and inmodel options in proc logistic with a few data steps. We will be using the hsb2.sas7bdat dataset.
data hsb2; set indata.hsb2; honcomp = (write >=60); run;
Example 1: Main effect with a continuous covariate
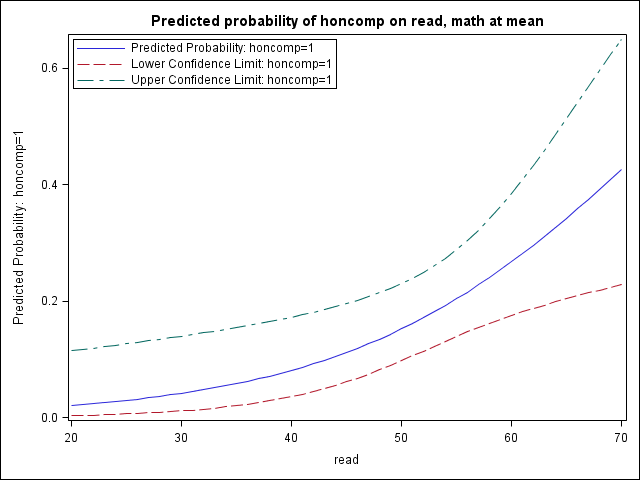
First let’s consider a logistic regression with two continuous covariates. In the regression output below, we see that both read and math are significant. We have also included outmodel in our regression so that we can save the regression parameters and apply them to another dataset. Let us focus on visualizing the effect of read when math is held at its mean.
proc logistic data = hsb2 outmodel=pout;
model honcomp = read math;
run;
...< some output omitted >...
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 11.9251 1.7168 48.2483 <.0001
read 1 -0.0709 0.0259 7.4891 0.0062
math 1 -0.1266 0.0305 17.1745 <.0001
We can use proc sql to generate a macro variable that is equal to the mean of math and then use a do-loop over a range of possible read values to create a dataset toscore that contains combinations of predictor variable values for which we are interested in predicted probabilities.
proc sql; select mean(math) into :mmath from hsb2; quit; data toscore; do read = 20 to 70; math = &mmath; output; end; run; proc print data = toscore (obs = 10); run; Obs read math 1 20 52.645 2 21 52.645 3 22 52.645 4 23 52.645 5 24 52.645 6 25 52.645 7 26 52.645 8 27 52.645 9 28 52.645 10 29 52.645
We can again run proc logistic, this time referring back to the regression parameters we saved in the first run with the inmodel option. We indicate the dataset to which the model should be applied (toscore) and the values (predicted probability with score, confidence intervals with clm) we wish to include in the generated dataset (pred). Lastly, we graph the predicted probabilities and the confidence intervals that we generate.
proc logistic inmodel=pout; score clm data = toscore out=pred ; run; proc print data = pred (obs = 10); run; Obs read math I_honcomp P_0 P_1 LCL_0 UCL_0 LCL_1 UCL_1 1 20 52.645 0 0.97905 0.020954 0.88499 0.99649 0.003512 0.11501 2 21 52.645 0 0.97754 0.022459 0.88275 0.99604 0.003958 0.11725 3 22 52.645 0 0.97593 0.024069 0.88047 0.99554 0.004460 0.11953 4 23 52.645 0 0.97421 0.025792 0.87813 0.99497 0.005025 0.12187 5 24 52.645 0 0.97236 0.027635 0.87574 0.99434 0.005660 0.12426 6 25 52.645 0 0.97039 0.029606 0.87329 0.99363 0.006374 0.12671 7 26 52.645 0 0.96829 0.031713 0.87079 0.99282 0.007177 0.12921 8 27 52.645 0 0.96604 0.033964 0.86823 0.99192 0.008078 0.13177 9 28 52.645 0 0.96363 0.036369 0.86560 0.99091 0.009091 0.13440 10 29 52.645 0 0.96106 0.038937 0.86291 0.98977 0.010226 0.13709 proc sgplot data=pred; title "Predicted probability of honcomp on read, math at mean"; series x=read y=P_1; series x=read y=LCL_1; series x=read y=UCL_1; keylegend / across = 1 location=inside position=topleft; run; quit;
Example 2: Categorical-by-continuous interaction with a continuous covariate
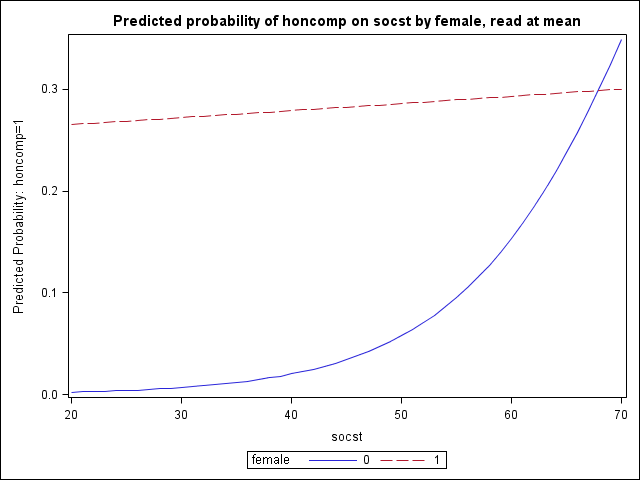
Next we consider a logistic regression where we have a significant categorical-by-continuous interaction that we wish to better understand. Our outcome is again honcomp and our model suggests that the relationship between socst and honcomp differs by level of female. We can hold our other covariate read at its mean and look at the predicted probability of honcomp on socst by female.
The overall process is the same as in Example 1. We are simply adding another do-loop when we generate toscore2, our dataset of predictor value combinations, so that we cycle through values of socst for both female = 0 and female = 1. In the plot, we leave out confidence intervals for a clearer picture (though they could easily be added).
proc logistic data = hsb2 outmodel=pout2; model honcomp = female|socst read; run; ...< some output omitted >... The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 14.7664 2.9554 24.9648 <.0001 female 1 -7.1249 3.1138 5.2357 0.0221 socst 1 -0.1084 0.0470 5.3286 0.0210 female*socst 1 0.1050 0.0526 3.9861 0.0459 read 1 -0.1255 0.0277 20.4930 <.0001 proc sql; select mean(read) into :mread from hsb2; quit; data toscore2; do female = 0 to 1; do socst = 20 to 70; read = &mread; output; end; end; run; proc logistic inmodel=pout2; score clm data = toscore2 out=pred2 ; run; proc sgplot data=pred2; title "Predicted probability of honcomp on socst by female, read at mean"; series x=socst y=P_1 / group = female; run; quit;
Example 3: Continuous by continuous interaction with a continuous covariate
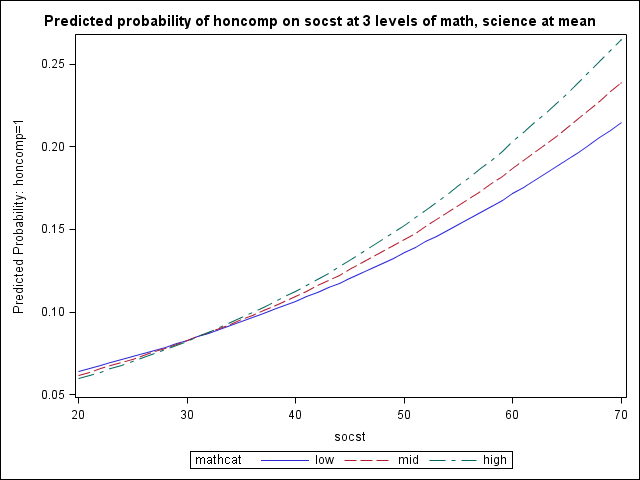
Lastly we consider a logistic regression where we have a significant continuous-by-continuous interaction and an additional covariate. Our outcome is again honcomp and our continuous variables math and socst interact significantly. We choose one of these variables (socst) to be represented continuously and we can look at its effect on the predicted probabilities of honcomp for high, mid, and low values of the other interaction variable (math). The remaining covariate (science) is held at its mean.
The overall process is the same as in Examples 1 and 2. In our toscore3 dataset, we enter our three levels of math and create an additional variable mathcat that is primarily for graphing purposes.
proc logistic data = hsb2 outmodel=pout3; model honcomp = math|socst science; run; ...< some output omitted >... The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -3.1784 7.6480 0.1727 0.6777 math 1 0.1675 0.1449 1.3365 0.2476 socst 1 0.2523 0.1451 3.0221 0.0821 math*socst 1 -0.00539 0.00266 4.0948 0.0430 science 1 -0.0443 0.0287 2.3780 0.1231 proc sql; select stderr(math) into :sdmath from hsb2; select mean(science) into :mscience from hsb2; quit; data toscore3; do socst = 20 to 70; science = &mscience; * low math; math = &mmath - &sdmath; mathcat = "low "; output; * mean math; math = &mmath; mathcat = "mid "; output; * high math; math = &mmath + &sdmath; mathcat = "high"; output; end; run; proc logistic inmodel=pout3; score clm data = toscore3 out=pred3; run; proc sgplot data=pred3; title "Predicted probability of honcomp on socst at 3 levels of math, science at mean"; series x=socst y=P_1 / group = mathcat; run; quit;