In this chapter, the data set is popular.
Table 4.1
Part 1: The variable sex is a fixed effect, not centered.
proc mixed data = pop ; model popular = sex/solution; random intercept / subject = school type = un; run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.8622
Residual 0.4599
Fit Statistics
-2 Res Log Likelihood 4492.9
AIC (smaller is better) 4496.9
AICC (smaller is better) 4496.9
BIC (smaller is better) 4502.1
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 1728.72 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 4.8972 0.09530 99 51.39 <.0001
SEX 0.8437 0.03096 1899 27.25 <.0001
Part 2: The variable sex is a fixed effect, raw centered. We first created a centered variable csex for sex.
proc means data = pop mean ;
var sex;
run;
Analysis Variable : SEX pupil sex
Mean
------------
0.4870000
------------
data popc; set pop; csex = sex - .487; run; proc mixed data = popc ; model popular = csex/solution; random intercept / subject = school type = un; run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.8622
Residual 0.4599
Fit Statistics
-2 Res Log Likelihood 4492.9
AIC (smaller is better) 4496.9
AICC (smaller is better) 4496.9
BIC (smaller is better) 4502.1
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 1728.72 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 5.3081 0.09410 99 56.41 <.0001
csex 0.8437 0.03096 1899 27.25 <.0001
Part 3: The variable sex is included as a random effect.
proc mixed data = pop ; model popular = sex/solution; random intercept sex/ subject = school type = un; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.9402
UN(2,1) SCHOOL -0.1410
UN(2,2) SCHOOL 0.2725
Residual 0.3924
Fit Statistics
-2 Res Log Likelihood 4336.3
AIC (smaller is better) 4344.3
AICC (smaller is better) 4344.3
BIC (smaller is better) 4354.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1885.30 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 4.8901 0.09901 99 49.39 <.0001
SEX 0.8431 0.05963 99 14.14 <.0001
Part 4: The variable sex is centered and is a random effect.
proc mixed data = popc ; model popular = csex/solution; random intercept csex/ subject = school type = un; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.8675
UN(2,1) SCHOOL -0.00825
UN(2,2) SCHOOL 0.2725
Residual 0.3924
Fit Statistics
-2 Res Log Likelihood 4336.3
AIC (smaller is better) 4344.3
AICC (smaller is better) 4344.3
BIC (smaller is better) 4354.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1885.30 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 5.3007 0.09424 99 56.25 <.0001
csex 0.8431 0.05963 99 14.14 <.0001
Table 4.2 on page 60.
Part 1: No interaction, no centering.
proc mixed data = pop ; model popular = sex texp /solution; random intercept sex/ subject = school type = un; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.4116
UN(2,1) SCHOOL 0.02089
UN(2,2) SCHOOL 0.2733
Residual 0.3925
Fit Statistics
-2 Res Log Likelihood 4275.9
AIC (smaller is better) 4283.9
AICC (smaller is better) 4283.9
BIC (smaller is better) 4294.3
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 3.3400 0.1608 98 20.77 <.0001
SEX 0.8431 0.05969 99 14.13 <.0001
TEXP 0.1084 0.01022 1800 10.61 <.0001
Part 2: With interaction, but no centering.
data pop1; set pop; genxexp = sex*texp; run; proc mixed data = pop1 ; model popular = sex texp genxexp/solution; random intercept sex /subject = school type=un ; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.4120
UN(2,1) SCHOOL 0.02343
UN(2,2) SCHOOL 0.2264
Residual 0.3924
Fit Statistics
-2 Res Log Likelihood 4268.4
AIC (smaller is better) 4276.4
AICC (smaller is better) 4276.5
BIC (smaller is better) 4286.9
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 3.3135 0.1610 98 20.58 <.0001
SEX 1.3296 0.1330 98 9.99 <.0001
TEXP 0.1102 0.01023 1800 10.77 <.0001
genxexp -0.03403 0.008457 1800 -4.02 <.0001
Part 3: Centering, but no interaction. We first created new variables csex and ctexp and their interaction term.
proc means data = pop mean; var sex texp; run; The MEANS Procedure Variable Label Mean ------------------------------------------------------- SEX pupil sex 0.4870000 TEXP teacher experience in years 14.2630000 ------------------------------------------------------- data pop2; set pop; csex = sex - 0.487; ctexp = texp - 14.263; cx = csex*ctexp; run; proc mixed data = pop2 ; model popular = csex ctexp /solution; random intercept csex /subject = school type=un ; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.4967
UN(2,1) SCHOOL 0.1540
UN(2,2) SCHOOL 0.2733
Residual 0.3925
Fit Statistics
-2 Res Log Likelihood 4275.9
AIC (smaller is better) 4283.9
AICC (smaller is better) 4283.9
BIC (smaller is better) 4294.3
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 5.2960 0.07192 98 73.63 <.0001
csex 0.8431 0.05969 99 14.13 <.0001
ctexp 0.1084 0.01022 1800 10.61 <.0001
Part 4: Centering and with interaction.
proc mixed data = pop2 ; model popular = csex ctexp cx/solution; random intercept csex /subject = school type=un ; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.4885
UN(2,1) SCHOOL 0.1337
UN(2,2) SCHOOL 0.2264
Residual 0.3924
Fit Statistics
-2 Res Log Likelihood 4268.4
AIC (smaller is better) 4276.4
AICC (smaller is better) 4276.5
BIC (smaller is better) 4286.9
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 5.2969 0.07135 98 74.24 <.0001
csex 0.8442 0.05562 98 15.18 <.0001
ctexp 0.09366 0.01085 1800 8.63 <.0001
cx -0.03403 0.008457 1800 -4.02 <.0001
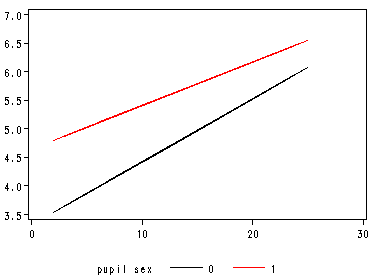
Figure 4.3. Regression lines for popularity of girls and boys, predicted by teacher experience, texp.
This uses model in Part 2 of Table 4.2. We will have to manually create the predicted values by the fixed part of the model.
data fig4_3;
set pop1;
pred = 3.3135 + 1.3296* sex + 0.1102*texp -0.03403*genxexp;
run;
axis1 order = (0 to 30 by 10) minor = none label = (" ");
axis2 order = (3.5 to 7 by .5) minor = none label = (" ");
symbol i = join;
proc gplot data = fig4_3;
plot pred*texp = sex /vaxis =axis2 haxis=axis1;
run;
quit;
Table 4.3
Part 1: Intercept only.
This has been done in Chapter 2, Table 2.1.
Part 2: The variable sex is included as a fixed effect.
This has been done in Table 4.1.
Part 3: The variable texp is also included.
proc mixed data = pop1 ; model popular = sex texp / outp = test solution; random intercept /subject = school type=un ; run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 0.4860
Residual 0.4599
Fit Statistics
-2 Res Log Likelihood 4444.4
AIC (smaller is better) 4448.4
AICC (smaller is better) 4448.4
BIC (smaller is better) 4453.6
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 3.5607 0.1715 98 20.76 <.0001
SEX 0.8447 0.03095 1899 27.29 <.0001
TEXP 0.09345 0.01085 1899 8.61 <.0001
Part 4: This has been done in Table 4.2.
Part 5: This is done in Table 4.2.
Table 4.4 can be produced manually based on the equations provided in this section. We omit the calculation here.