Negative binomial regression is for modeling count variables, usually for over-dispersed count outcome variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
This page was updated using SAS 9.2.
Examples of negative binomial regression
Example 1. School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include the type of program in which the student is enrolled and a standardized test in math.
Example 2. A health-related researcher is studying the number of hospital visits in past 12 months by senior citizens in a community based on the characteristics of the individuals and the types of health plans under which each one is covered.
Description of the data
Let’s pursue Example 1 from above.
We have attendance data on 314 high school juniors from two urban high schools in the file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.sas7bdat. The response variable of interest is days absent, daysabs. The variable math gives the standardized math score for each student. The variable prog is a three-level nominal variable indicating the type of instructional program in which the student is enrolled.
Let’s look at the data. It is always a good idea to start with descriptive statistics and plots.
proc means data = nb_data; var daysabs math; run;
The MEANS Procedure Variable Label N Mean Std Dev Minimum Maximum ----------------------------------------------------------------------------------------------------- DAYSABS number days absent 314 5.9554140 7.0369576 0 35.0000000 MATH ctbs math pct rank 314 48.2675159 25.3623913 1.0000000 99.0000000 -----------------------------------------------------------------------------------------------------
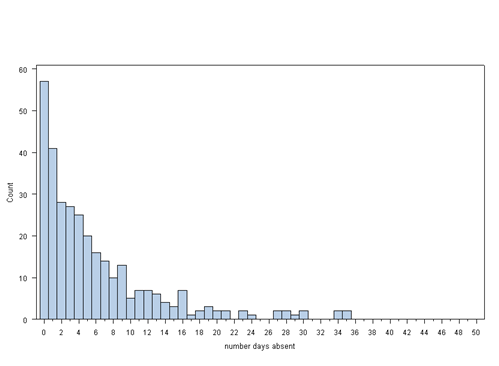
proc univariate data = nb_data noprint; histogram daysabs / midpoints = 0 to 50 by 1 vscale = count ; run;
Each variable has 314 valid observations and their distributions seem quite reasonable. The mean of our outcome variable is much lower than its variance.
Let’s continue with our description of the variables in this dataset. The table below shows the average numbers of days absent by program type and seems to suggest that program type is a good candidate for predicting the number of days absent, our outcome variable, because the mean value of the outcome appears to vary by prog. The variances within each level of prog are higher than the means within each level. These are the conditional means and variances. These differences suggest that over-dispersion is present and that a Negative Binomial model would be appropriate.
proc sort data = nb_data;
by prog;
run;
proc means mean var n data = nb_data;
by prog;
var daysabs;
run;
PROG=1
The MEANS Procedure
Analysis Variable : DAYSABS number days absent
Mean Variance N
-----------------------------------
10.6500000 67.2589744 40
-----------------------------------
PROG=2
Analysis Variable : DAYSABS number days absent
Mean Variance N
-----------------------------------
6.9341317 55.4474425 167
-----------------------------------
PROG=3
Analysis Variable : DAYSABS number days absent
Mean Variance N
-----------------------------------
2.6728972 13.9391642 107
-----------------------------------
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Negative binomial regression – Negative binomial regression can be used for over-dispersed count data, that is when the conditional variance exceeds the conditional mean. It can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression and it has an extra parameter to model the over-dispersion. If the conditional distribution of the outcome variable is over-dispersed, the confidence intervals for the Negative binomial regression are likely to be narrower as compared to those from a Poisson regression model.
- Poisson regression – Poisson regression is often used for modeling count data. Poisson regression has a number of extensions useful for count models.
- Zero-inflated regression model – Zero-inflated models attempt to account for excess zeros. In other words, two kinds of zeros are thought to exist in the data, "true zeros" and "excess zeros". Zero-inflated models estimate two equations simultaneously, one for the count model and one for the excess zeros.
- OLS regression – Count outcome variables are sometimes log-transformed and analyzed using OLS regression. Many issues arise with this approach, including loss of data due to undefined values generated by taking the log of zero (which is undefined), as well as the lack of capacity to model the dispersion.
Negative binomial regression analysis
Negative binomial models can be estimated in SAS using proc genmod. On the class statement we list the variable prog. After prog, we use two options, which are given in parentheses. The param=ref option changes the coding of prog from effect coding, which is the default, to reference coding. The ref=first option changes the reference group to the first level of prog. We have used two options on the model statement. The type3 option is used to get the multi-degree-of-freedom test of the categorical variables listed on the class statement, and the dist = negbin option is used to indicate that a negative binomial distribution should be used.
proc genmod data = nb_data; class prog (param=ref ref=first); model daysabs = math prog / type3 dist=negbin; run;
The GENMOD Procedure
Model Information
Data Set WORK.NB_DATA
Distribution Negative Binomial
Link Function Log
Dependent Variable DAYSABS number days absent
Number of Observations Read 314
Number of Observations Used 314
Class Level Information
Design
Class Value Variables
PROG 1 0 0
2 1 0
3 0 1
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 310 358.5193 1.1565
Scaled Deviance 310 358.5193 1.1565
Pearson Chi-Square 310 339.8771 1.0964
Scaled Pearson X2 310 339.8771 1.0964
Log Likelihood 2151.5227
Full Log Likelihood -865.6289
AIC (smaller is better) 1741.2578
AICC (smaller is better) 1741.4526
BIC (smaller is better) 1760.0048
Algorithm converged.
Analysis Of Maximum Likelihood Parameter Estimates
Standard Wald 95% Confidence Wald
Parameter DF Estimate Error Limits Chi-Square Pr > ChiSq
Intercept 1 2.6153 0.1964 2.2304 3.0001 177.40 <.0001
MATH 1 -0.0060 0.0025 -0.0109 -0.0011 5.71 0.0168
PROG 2 1 -0.4408 0.1826 -0.7986 -0.0829 5.83 0.0158
PROG 3 1 -1.2787 0.2020 -1.6745 -0.8828 40.08 <.0001
Dispersion 1 0.9683 0.0995 0.7916 1.1844
NOTE: The negative binomial dispersion parameter was estimated by maximum likelihood.
LR Statistics For Type 3 Analysis
Chi-
Source DF Square Pr > ChiSq
MATH 1 5.61 0.0179
PROG 2 45.05 <.0001
this test. The non-significant p-value suggests that the negative binomial model is a good fit for the data.
data test; pval = 1 - probchi(339.8771, 310); run; proc print data = test; run; Obs pval 1 0.11703
We can also see the results as incident rate ratios by using estimate statements with the exp option.
proc genmod data = nb_data; class prog (param=ref ref=first); model daysabs = math prog / type3 dist=negbin; estimate 'prog 2' prog 1 0 / exp; estimate 'prog 3' prog 0 1 / exp; estimate 'math' math 1 / exp; run;< - some output omitted - >Contrast Estimate Results Mean Mean L'Beta Standard L'Beta Chi- Label Estimate Confidence Limits Estimate Error Alpha Confidence Limits Square prog 2 0.6435 0.4500 0.9204 -0.4408 0.1826 0.05 -0.7986 -0.0829 5.83 Exp(prog 2) 0.6435 0.1175 0.05 0.4500 0.9204 prog 3 0.2784 0.1874 0.4136 -1.2787 0.2020 0.05 -1.6745 -0.8828 40.08 Exp(prog 3) 0.2784 0.0562 0.05 0.1874 0.4136 math 0.9940 0.9892 0.9989 -0.0060 0.0025 0.05 -0.0109 -0.0011 5.71 Exp(math) 0.9940 0.0025 0.05 0.9892 0.9989
The output above indicates that the incident rate for prog=2 is 0.64 times the incident rate for the reference group (prog=1). Likewise, the incident rate for prog=3 is 0.28 times the incident rate for the reference group holding the other variables constant. The percent change in the incident rate of daysabs is a 1% decrease (1 - .99) for every unit increase in math.
The form of the model equation for negative binomial regression is the same as that for Poisson regression. The log of the outcome is predicted with a linear combination of the predictors:
log(daysabs) = Intercept + b1(prog=2) + b2(prog=3) + b3math.
This implies:
daysabs = exp(Intercept + b1(prog=2) + b2(prog=3)+ b3math) = exp(Intercept) * exp(b1(prog=2)) * exp(b2(prog=3)) * exp(b3math)
The coefficients have an additive effect in the log(y) scale and the IRR have a multiplicative effect in the y scale. The dispersion parameter in negative binomial regression does not effect the expected counts, but it does effect the estimated variance of the expected counts.
For additional information on the various metrics in which the results can be presented, and the interpretation of such, please see Regression Models for Categorical Dependent Variables Using Stata, Second Edition by J. Scott Long and Jeremy Freese (2006).
Below we use estimate statements to calculate the predicted number of events at each level of prog, holding all other variables (in this example, math) in the model at their means.
proc genmod data = nb_data;
class prog (param=ref ref=first);
model daysabs = math prog / type3 dist=negbin;
estimate 'prog 1' intercept 1 prog 0 0 math 48.2675 / exp;
estimate 'prog 2' intercept 1 prog 1 0 math 48.2675 / exp;
estimate 'prog 3' intercept 1 prog 0 1 math 48.2675 / exp;
run;
< - some output omitted - >
Contrast Estimate Results
Mean Mean L'Beta Standard L'Beta Chi-
Label Estimate Confidence Limits Estimate Error Alpha Confidence Limits Square
prog 1 10.2369 7.4291 14.1058 2.3260 0.1636 0.05 2.0054 2.6466 202.22
Exp(prog 1) 10.2369 1.6744 0.05 7.4291 14.1058
prog 2 6.5879 5.5916 7.7618 1.8852 0.0837 0.05 1.7213 2.0492 507.76
Exp(prog 2) 6.5879 0.5512 0.05 5.5916 7.7618
prog 3 2.8501 2.2720 3.5753 1.0473 0.1157 0.05 0.8207 1.2740 82.00
Exp(prog 3) 2.8501 0.3296 0.05 2.2720 3.5753
In the output above, we see that the predicted number of events for level 1 of prog is about 10.24, holding math at its mean. The predicted number of events for level 2 of prog is lower at 6.59, and the predicted number of events for level 3 of prog is about 2.85. Note that the predicted count of level 2 of prog is (6.5879/10.2369) = 0.64 times the predicted count for level 1 of prog. This matches what we saw in the after in the incident rate ratio output table.
We can similarly obtain the predicted number of events for values of math while holding prog constant.
proc genmod data = nb_data;
class prog (param=ref ref=first);
model daysabs = math prog / type3 dist=negbin;
estimate 'math 20' intercept 1 prog 0 0 math 20 / exp;
estimate 'math 40' intercept 1 prog 0 0 math 40 / exp;
run;
Contrast Estimate Results
Mean Mean L'Beta Standard L'Beta Chi-
Label Estimate Confidence Limits Estimate Error Alpha Confidence Limits Square
math 20 12.1267 8.6305 17.0391 2.4954 0.1735 0.05 2.1553 2.8355 206.80
Exp(math 20) 12.1267 2.1043 0.05 8.6305 17.0391
math 40 10.7569 7.8092 14.8172 2.3755 0.1634 0.05 2.0553 2.6958 211.38
Exp(math 40) 10.7569 1.7576 0.05 7.8092 14.8172
The table above shows that when prog held at its reference level and math at 20, the predicted count (or average number of days absent) is about 12.13; when prog held at its reference level and math at 40, the predicted count is about 10.76. If we compare the predicted counts at these two levels of math, we can see that the ratio is (10.7569/12.1267) = 0.887. This matches the IRR of 0.994 for a 20 unit change: 0.994^20 = 0.887.
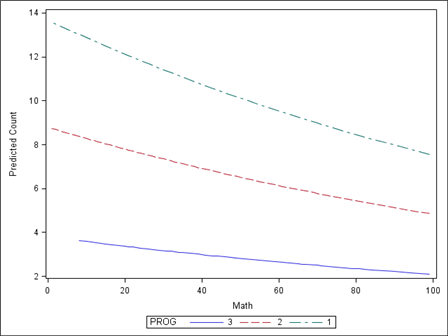
You can graph the predicted number of events using the commands below. Proc genmod must be run with the output statement to obtain the predicted values in a dataset we called pred1. We then sorted our data by the predicted values and created a graph with proc sgplot.
The graph indicates that the most days absent are predicted for those in program 1. The lowest number of predicted days absent is for those students in program 3.
proc genmod data = nb_data; class prog (param=ref ref=first); model daysabs = math prog / type3 dist=negbin; output out = nb_pred predicted = pred1; run; proc sort data = nb_pred; by pred1; run; proc sgplot data = nb_pred; series x=math y=pred1 / group = prog; run;
Things to consider
- It is not recommended that negative binomial models be applied to small samples.
- Negative binomial models assume that only one process generates the data. If more than one process generates the data, then it is possible to have more 0s than expected by the negative binomial model; in this case, a zero-inflated model (either zero-inflated Poisson or zero-inflated negative binomial) may be more appropriate.
- If the data generating process does not allow for any 0s (such as the number of days spent in the hospital), then a zero-truncated model may be more appropriate. Such models can be estimated with proc countreg.
- Count data often have an exposure variable, which indicates the number of times the event could have happened. This variable should be incorporated into your negative binomial model with the use of the offset option on the model statement.
- The outcome variable in a negative binomial regression cannot have negative numbers.
References
- Long, J. S. 1997. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
- Long, J. S. and Freese, J. 2006. Regression Models for Categorical Dependent Variables Using Stata, Second Edition. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. 2009. Microeconometrics Using Stata. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. 1998. Regression Analysis of Count Data. New York: Cambridge Press.
- Cameron, A. C. Advances in Count Data Regression Talk for the Applied Statistics Workshop, March 28, 2009. http://cameron.econ.ucdavis.edu/racd/count.html .
- Dupont, W. D. 2002. Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data. New York: Cambridge Press.
See also
- Annotated output for negative binomial regression
- SAS Online Manual