Note: This example is done in PROC LCA 1.3.2. PROC LCA is developed for SAS version 9.4 for Windows by the Methodology Center at Penn State. It can be downloaded from their website.
Examples of Latent Class Analysis
Example 1. You are interested in studying drinking behavior among adults. Rather than conceptualizing drinking behavior as a continuous variable, you conceptualize it as forming distinct categories or typologies. For example, you think that people fall into one of three different types: abstainers, social drinkers and alcoholics. Since you cannot directly measure what category someone falls into, this is a latent variable (a variable that cannot be directly measured). However, you do have a number of indicators that you believe are useful for categorizing people into these different categories. Using these indicators, you would like to:
- Create a model that permits you to categorize these people into three different types of drinkers, hopefully fitting your conceptualization that there are abstainers, social drinkers and alcoholics.
- Be able to categorize people as to what kind of drinker they are.
- Count how many people would be considered abstainers, social drinkers and alcoholics.
- Determine whether three latent classes is the right number of classes (i.e., are there only two types of drinkers or perhaps are there as many as four types of drinkers).
Example 2. High school students vary in their success in school. This might be indicated by the grades one gets, the number of absences one has, the number of truancies one has, and so forth. A traditional way to conceptualize this might be to view “degree of success in high school” as a latent variable (one that you cannot directly measure) that is normally distributed. However, you might conceptualize some students who are struggling and having trouble as forming a different category, perhaps a group you would call “at risk” (or in older days they would be called “juvenile delinquents”). Using indicators like grades, absences, truancies, tardiness, suspensions, etc., you might try to identify latent class memberships based on high school success.
Description of the Data
Let’s pursue Example 1 from above. We have a hypothetical data file that we created that contains 9 fictional measures of drinking behavior. For each measure, the person would be asked whether the description applies to him/herself (yes or no). The 9 measures are
- I like to drink
- I drink hard liquor
- I have drank in the morning
- I have drank at work
- I drink to get drunk
- I like the taste of alcohol
- I drink help me sleep
- Drinking interferes with my relationships
- I frequently visit bars
We have made up data for 1000 respondents and stored the data in a file called lca1.dat, which is a comma-separated file with the subject id followed by the responses to the 9 questions, coded 1 for yes and 0 for no. We listed the first ten observations and the mean and standard deviation for each item.
data lca1; infile "d:\downloads\lca1.dat" delimiter=","; input id item1 item2 item3 item4 item5 item6 item7 item8 item9; label item1 = "I like to drink" item2 = "I drink hard liquor" item3 ="I have drank in the morning" item4 = "I have drank at work" item5 = "I drink to get drunk" item6 = "I like the taste of alcohol" item7 = "I drink help me sleep" item8 = "Drinking interferes with my relationships" item9 = "I frequently visit bars"; run; options label nocenter nodate; proc print data = lca1 (obs=10) noobs; run; proc means data = lca1 mean std; var item1 - item9; run;
id item1 item2 item3 item4 item5 item6 item7 item8 item9 1 1 0 0 0 0 0 0 0 0 2 1 1 0 1 1 1 1 0 0 3 1 0 0 0 0 0 0 0 0 4 1 0 0 0 0 1 1 0 0 5 1 0 0 0 1 0 0 0 1 6 0 1 0 0 0 1 0 0 0 7 1 1 0 0 0 0 0 0 1 8 1 0 1 0 0 0 0 0 0 9 1 0 0 0 0 0 0 1 0 10 0 0 0 0 0 1 0 0 0
Variable Label Mean Std Dev item1 I like to drink 0.693 0.46148 item2 I drink hard liquor 0.291 0.454451 item3 I have drank in the morning 0.084 0.277527 item4 I have drank at work 0.09 0.286325 item5 I drink to get drunk 0.199 0.399448 item6 I like the taste of alcohol 0.282 0.450199 item7 I drink help me sleep 0.139 0.34612 item8 Drinking interferes with my relationships 0.167 0.373163 item9 I frequently visit bars 0.277 0.44774
Before we show how you can analyze this with Latent Class Analysis, let’s consider some other methods that you might use:
- Cluster Analysis – You could use cluster analysis for data like these. However, cluster analysis is not based on a statistical model. It can tell you how the cases are clustered into groups, but it does not provide information such as the probability that a given person is an alcoholic or abstainer. Also, cluster analysis would not provide information such as: given that someone said “yes” to drinking at work, what is the probability that they are an alcoholic?
- Factor Analysis – Because the term “latent variable” is used, you might be tempted to use factor analysis since that is a technique used with latent variables. However, factor analysis is used for continuous and usually normally distributed latent variables, where this latent variable, e.g., alcoholism, is categorical.
SAS Results Using Latent Class Analysis with three classes
Let’s say that our theory indicates that there should be three latent classes. So we will run a latent class analysis model with three classes. With version 1.1.3, values of the items should be 1 and higher. In other words, 0/1 variables are not allowed. Therefore, in the DATA step below, we recode the items so they will be coded as 1/2.
data lca2; set lca1; array it(9) item1 - item9; do i = 1 to 9; it(i) = 2 - it(i); end; drop i; run;
The SAS syntax using PROC LCA is shown below. The option outparam allows us to save the final parameter estimates for each item and each class and outpost allows us to save the posterior probabilities for each observation.
proc lca data = lca2 OUTPARAM = test outpost = lca1_post; nclass 3; id id; items item1 item2 item3 item4 item5 item6 item7 item8 item9; categories 2 2 2 2 2 2 2 2 2 ; seed 123741; run;Data Summary, Model Information, and Fit Statistics (EM Algorithm) Number of subjects in dataset: 1000 Number of subjects in analysis: 1000 Number of measurement items: 9 Response categories per item: 2 2 2 2 2 2 2 2 2 Number of groups in the data: 1 Number of latent classes: 3 Rho starting values were randomly generated (seed = 123741). No parameter restrictions were specified (freely estimated). The model converged in 429 iterations. Maximum number of iterations: 5000 Convergence method: maximum absolute deviation (MAD) Convergence criterion: 0.000001000 ============================================= Fit statistics: ============================================= Log-likelihood: -4231.70 G-squared: 319.96 AIC: 377.96 BIC: 520.28 CAIC: 549.28 Adjusted BIC: 428.17 Entropy: 0.55 Degrees of freedom: 482Parameter Estimates Class membership probabilities: Gamma estimates (standard errors) Class: 1 2 3 0.5573 0.0793 0.3634 (0.1752) (0.0243) (0.1839) Item response probabilities: Rho estimates (standard errors) Response category 1: Class: 1 2 3 item1 : 0.9084 0.9233 0.3125 (0.0878) (0.0411) (0.2117) item2 : 0.3375 0.5461 0.1641 (0.0569) (0.0782) (0.0415) item3 : 0.0668 0.4264 0.0357 (0.0175) (0.0938) (0.0159) item4 : 0.0655 0.4180 0.0560 (0.0190) (0.0817) (0.0168) item5 : 0.2192 0.7655 0.0444 (0.0532) (0.1000) (0.0371) item6 : 0.3197 0.4710 0.1830 (0.0432) (0.0763) (0.0453) item7 : 0.1128 0.5124 0.0977 (0.0213) (0.0929) (0.0220) item8 : 0.1399 0.6193 0.1099 (0.0272) (0.1081) (0.0224) item9 : 0.3249 0.3488 0.1878 (0.0400) (0.0698) (0.0402) Response category 2: Class: 1 2 3 item1 : 0.0916 0.0767 0.6875 (0.0878) (0.0411) (0.2117) item2 : 0.6625 0.4539 0.8359 (0.0569) (0.0782) (0.0415) item3 : 0.9332 0.5736 0.9643 (0.0175) (0.0938) (0.0159) item4 : 0.9345 0.5820 0.9440 (0.0190) (0.0817) (0.0168) item5 : 0.7808 0.2345 0.9556 (0.0532) (0.1000) (0.0371) item6 : 0.6803 0.5290 0.8170 (0.0432) (0.0763) (0.0453) item7 : 0.8872 0.4876 0.9023 (0.0213) (0.0929) (0.0220) item8 : 0.8601 0.3807 0.8901 (0.0272) (0.1081) (0.0224) item9 : 0.6751 0.6512 0.8122 (0.0400) (0.0698) (0.0402)
Conditional Probabilities
First, the probability of answering “yes” to each question is shown for each type of drinker (latent class). Looking at the pattern of responses for all classes gives you an overall picture of the meaning of the three classes that are identified and helps us create descriptive labels for the classes. We are hoping to find three classes that correspond to abstainers, social drinkers, and alcoholics. Abstainers would have a pattern that they generally avoid drinking, social drinkers would show a pattern of drinking but generally in moderation and seldom in self-destructive ways, while alcoholics would show a pattern of drinking frequently and in very self-destructive ways.
The SAS output shows a section labeled:
Item response probabilities: Rho estimates (standard errors)
which contains the conditional probabilities as describe above, but it is hard to read. The results have reformatted to make the output easier to read, shown below. Each row represents a different item, and the three columns of numbers are the probabilities of answering “yes” to the item given that you belonged to that class. So, if you belong to Class 1, you have a 90.8% probability of saying “yes, I like to drink”. By contrast, if you belong to Class 3, you have a 31.2% chance of saying “yes, I like to drink”.
| Class 1 | Class 2 | Class 3 | Item Label | |
| ITEM1 | 0.908 | 0.923 | 0.312 | I like to drink |
| ITEM2 | 0.337 | 0.546 | 0.164 | I drink hard liquor |
| ITEM3 | 0.067 | 0.426 | 0.036 | I have drank in the morning |
| ITEM4 | 0.065 | 0.418 | 0.056 | I have drank at work |
| ITEM5 | 0.219 | 0.765 | 0.044 | I drink to get drunk |
| ITEM6 | 0.32 | 0.471 | 0.183 | I like the taste of alcohol |
| ITEM7 | 0.113 | 0.512 | 0.098 | I drink help me sleep |
| ITEM8 | 0.14 | 0.619 | 0.11 | Drinking interferes with my relationships |
| ITEM9 | 0.325 | 0.349 | 0.188 | I frequently visit bars |
Looking at Item1, those in Class 1 and Class 2 really like to drink (with 90.8% and 92.3% saying yes) while those in Class 3 are not so fond of drinking (they have only a 31.2% probability of saying they like to drink). Jumping to Item5, 76.5% of those in Class 2 say they drink to get drunk, while 21.9% of those in Class 1 agreed to that, and only 4.4% of those in Class 3 say that.
Perhaps Class 2 may be labeled as “alcoholics”. Focusing just on Class 2 (looking at that column), they really like to drink (92%), drink hard liquor (54.6%), a pretty large number say they have drank in the morning and at work (42.6% and 41.8%), and well over half say drinking interferes with their relationships (61.9%).
It seems that those in Class 3 are the “abstainers” we were hoping to find. Not many of them like to drink (31.2%), few like the taste of alcohol (18.3%), few frequently visit bars (18.8%), and for the rest of the questions they rarely answered “yes”.
This leaves Class 1. Might they fit the idea of the “social drinker”? They like to drink (90.8%), but they don’t drink hard liquor as often as Class 2 (33.7% versus 54.6%). They rarely drink in the morning or at work (6.7% and 6.5%) and rarely say that drinking interferes with their relationships (14%). They say they frequently visit bars similar to Class 2 (32.5% versus 34.9%), but that might make sense. Both the social drinkers and alcoholics are similar in how much they like to drink and how frequently they go to bars, but differ in key ways such as drinking at work, drinking in the morning, and the impact of drinking on their relationships.
While we should study these conditional probabilities some more, I think we can start to assign labels to these classes. As I hypothesized, the classes seem to make sense to be labeled “social drinkers” (Class 1), “alcoholics” (Class 2), and “abstainers” (Class 3).”
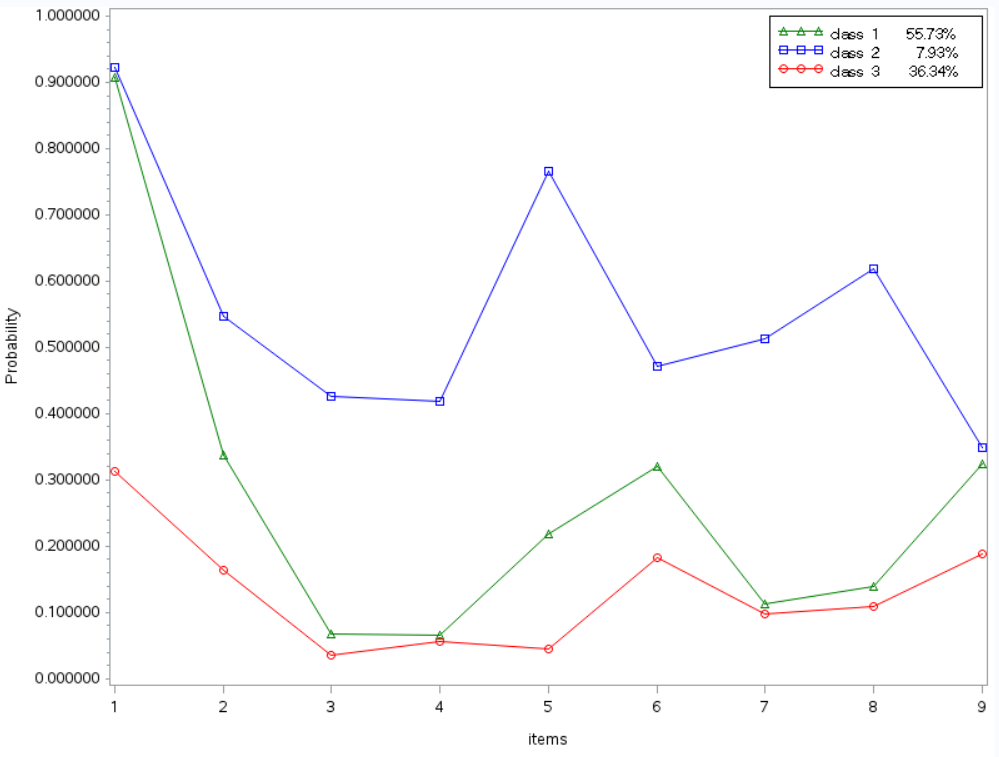
We can also take the results from the above table and express it as a graph. The x-axis represents the item number and the y-axis represents the probability of answering “yes” to the given item, given that you belong to a particular drinking class. The three drinking classes are represented as the three different lines.
*plot;
data test2;
set test;
itemid = substr(variable, 5,2);
if _n_ = 1 then do;
call symput('p1', put(estlc1, percent10.2));
call symput('p2', put(estlc2, percent10.2));
call symput('p3', put(estlc3, percent10.2));
end;
run;
goptions reset = all;
symbol1 i=join v = triangle c=green;
symbol3 i=join v = circle c=red;
symbol2 i=join v = square c=blue;
axis1 label=(a=90 "Probability" );
axis2 label=("items");
legend down=3 label=none value=(font=swiss "class 1 &p1" "class 2 &p2" "class 3 &p3")
position=(top right inside) mode=share cborder=black;
proc gplot data = test2;
where respcat =1;
plot(estlc1 estlc2 estlc3)*itemid /vaxis = axis1 legend=legend1 haxis=axis2 overlay;
run;
quit;
Class Membership
For each person, PROC LCA will estimate what class the person belongs to (i.e., what type of drinker the person is). For a given person, PROC LCA estimates the probability that the person belongs to the first, second, or third class. For example, for Subject 1 these probabilities might be 64% that the person belongs to the first class, 0.1% probability of belonging to the second class, and 35% of belonging to the third class. For such a person, the best guess would be that this person belongs to the first class since that is the modal probability. Other subjects will also be categorized into a single class using the same kind of rule. Note how the third subject has the same pattern of responses as the first subject and has the same predicted class probabilities.
The outpost option on the PROC LCA statement creates an output file which contains the original data used in the analysis (i.e., item1 to item9) followed by the probability estimates that the observation belongs to Class 1, Class2, and Class 3. Next, the class with the highest probability (the modal class) is shown. The first 10 observations are shown below.
proc print data = lca1_post (obs = 10) noobs;
run;
| id | item1 | item2 | item3 | item4 | item5 | item6 | item7 | item8 | item9 | POSTLC1 | POSTLC2 | POSTLC3 | BEST |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0.644384 | 0.001339 | 0.354277 | 1 |
| 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 0.098343 | 0.900471 | 0.001185 | 2 |
| 3 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0.644384 | 0.001339 | 0.354277 | 1 |
| 4 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 0.796411 | 0.025913 | 0.177676 | 1 |
| 5 | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 0.934042 | 0.025114 | 0.040844 | 1 |
| 6 | 2 | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 0.311499 | 0.002387 | 0.686115 | 3 |
| 7 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 0.903132 | 0.004933 | 0.091934 | 1 |
| 8 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0.765404 | 0.016531 | 0.218065 | 1 |
| 9 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 0.695444 | 0.014447 | 0.290109 | 1 |
| 10 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 0.148809 | 0.000483 | 0.850708 | 3 |
For the second observation, the pattern of responses to the items suggests that the person has a 9.8% chance of being in Class 1 (social drinkers), a 90% chance of being in Class 2 (alcoholics), and a 0.1% chance of being in Class 3 (abstainers). Note that these sum to 100% (since a person has to be in one of these classes). For this person, Class 2 is the most likely class, and SAS indicates that in the last column (BEST). One important point to note here is that for some subjects, the class membership is pretty well determined (like Subject 2), while it is a bit more ambiguous (like Subjects 1 and 3) where there is no single class that they certainly belong to.
Size of Classes
Once we have come up with a descriptive label for each of the classes, we can look at the number of people who are categorized into each of the classes. I predict that about 70% are social drinkers, 10% are alcoholics, and 20% of people are abstainers. I can compare my predictions to the results that SAS produces.
How many alcoholics are there? How many abstainers are there? How many social drinkers are there? One simple way we could determine this is by taking the information from the Class Membership above and doing a simple tabulation on the last column (BEST). Since PROC LCA doesn’t give this to you by default, you can run a simple frequency table using the code below.
proc freq data = lca1_post; table BEST; run;
| BEST | ||||
|---|---|---|---|---|
| BEST | Frequency | Percent | Cumulative Frequency | Cumulative Percent |
| 1 | 646 | 64.60 | 646 | 64.60 |
| 2 | 66 | 6.60 | 712 | 71.20 |
| 3 | 288 | 28.80 | 1000 | 100.00 |
Out of the 1,000 subjects we had, 646 (64.6%) are categorized as Class 1 (which we label as social drinkers), 66 (6.6%) are categorized as Class 2 (alcoholics), and 288 (28.8%) are categorized as Class 3 (abstainers). This is consistent with my hunches that most people are social drinkers, a very small portion are alcoholics, and a moderate portion are abstainers.
There is a second way we could compute the size of the classes. Consider Subject 1 from the above output on class membership. Rather than considering this person as entirely belonging to Class 1, we could allocate membership to the classes in proportion to the probability of being in each class. So, Subject 1 has fractional memberships in each class, 0.645 to Class 1, 0.001 to Class 2, and 0.354 to Class 3. SAS also computes the class sizes in this manner, as shown below.
Class membership probabilities: Gamma estimates (standard errors)
Class: 1 2 3
0.5573 0.0793 0.3634
(0.1752) (0.0243) (0.1839)
These two methods yield largely similar results, but this second method suggests that there are somewhat more abstainers (36.3%) compared to the previous method (28.8%) and slightly fewer social drinkers (55.7% compared to 64.6%), but these differences are not very troublesome to me.
Cautions, Flies in the Ointment
We have focused on a very simple example here just to get you started. Here are some problems to watch out for.
- Have you specified the right number of latent classes? Perhaps you have specified too many classes (i.e., people largely fall into 2 classes) or you may have specified too few classes (i.e., people really fall into 4 or more classes).
- Are some of your measures/indicators lousy? All of our measures were really useful in distinguishing what type of drinker the person was. However, say we had a measure that was “Do you like broccoli?”. This would be a poor indicator, and each type of drinker would probably answer in a similar way, so this question would be a good candidate to discard.
- Having developed this model to identify the different types of drinkers, we might be interested in trying to predict why someone is an alcoholic, or why someone is an abstainer. For example, we might be interested in whether parental drinking predicts being an alcoholic. Such analyses are possible, but not discussed here. (references forthcoming)
See Also
- Stat Books for Loan
- Latent Class Scaling Analysis by C. Mitchell Dayton
- Applied Latent Class Analysis Edited by Jacques A. Hagenaars and Allan L. McCutcheon
- Latent Class Analysis by Allan L. McCutcheon