Mixture models are measurement models that use observed variables as indicators of one or more nominal latent variables (i.e. categorical variables). One way to think about mixture models that one is attempting to identify subsets or "classes" of observations within the observed data. The latent variable (classes) is categorical, but the indicators may be either categorical or continuous. The term latent class analysis is often used to refer to a mixture model in which all of the observed indicator variables are categorical.
Mplus version 5.2 was used for these examples.
1.0 Latent class analysis
The examples on this page use a dataset with information on high school students’ academic histories. In the first example below, a 2 class model is estimated using four dichotomous variables as indicators (category 1 = no, category 2 = yes). The variables are whether the student had taken honors math (hm), honors English (he), or vocational classes (voc); and whether the student reported they were unlikely to go to college (nocol). The expected classes are academically oriented students (i.e. students who took honors classes, did not take vocational classes and reported they were likely to go to college), and students who are less academically oriented. The dataset for this example is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat.
The input file for this model is shown below. The usevariables option of the of the variables: command specifies which variables will be used in this analysis (necessary when not all of the variables in the dataset are used). The classes option identifies the name of the latent variable (in this case c), followed by the number of classes to be estimated in parentheses (in this case 2). Note that the class variable(s) can be assigned any valid variable name. The categorical option of the variables: command tells Mplus which variables are categorical. The type option of the analysis: command specifies the type of model to be estimated, in this case a mixture model.
TITLE: A latent class analysis (LCA) Data: file is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat; Variable: names are hm he voc nocol ach9-ach12; usevariables are hm he voc nocol ; classes = c (2); categorical = hm he voc nocol ; Analysis: type = mixture;
The output for this model is shown below.
INPUT READING TERMINATED NORMALLY
A latent class analysis (LCA)
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 4
Number of independent variables 0
Number of continuous latent variables 0
Number of categorical latent variables 1
Observed dependent variables
Binary and ordered categorical (ordinal)
HM HE VOC NOCOL
Categorical latent variables
C
Estimator MLR
Information matrix OBSERVED
Optimization Specifications for the Quasi-Newton Algorithm for
Continuous Outcomes
Maximum number of iterations 100
Convergence criterion 0.100D-05
Optimization Specifications for the EM Algorithm
Maximum number of iterations 500
Convergence criteria
Loglikelihood change 0.100D-06
Relative loglikelihood change 0.100D-06
Derivative 0.100D-05
Optimization Specifications for the M step of the EM Algorithm for
Categorical Latent variables
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Optimization Specifications for the M step of the EM Algorithm for
Censored, Binary or Ordered Categorical (Ordinal), Unordered
Categorical (Nominal) and Count Outcomes
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Maximum value for logit thresholds 15
Minimum value for logit thresholds -15
Minimum expected cell size for chi-square 0.100D-01
Optimization algorithm EMA
Random Starts Specifications
Number of initial stage random starts 10
Number of final stage optimizations 2
Number of initial stage iterations 10
Initial stage convergence criterion 0.100D+01
Random starts scale 0.500D+01
Random seed for generating random starts 0
Link LOGIT
Input data file(s)
https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat
Input data format FREE
SUMMARY OF CATEGORICAL DATA PROPORTIONS
HM
Category 1 0.678
Category 2 0.322
HE
Category 1 0.686
Category 2 0.314
VOC
Category 1 0.322
Category 2 0.678
NOCOL
Category 1 0.334
Category 2 0.666
RANDOM STARTS RESULTS RANKED FROM THE BEST TO THE WORST LOGLIKELIHOOD VALUES
Final stage loglikelihood values at local maxima, seeds, and initial stage start numbers:
-965.244 93468 3
-965.244 939021 8
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -965.244
H0 Scaling Correction Factor 1.013
for MLR
Information Criteria
Number of Free Parameters 9
Akaike (AIC) 1948.488
Bayesian (BIC) 1986.420
Sample-Size Adjusted BIC 1957.853
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit for the Binary and Ordered Categorical
(Ordinal) Outcomes
Pearson Chi-Square
Value 6.287
Degrees of Freedom 6
P-Value 0.3918
Likelihood Ratio Chi-Square
Value 5.605
Degrees of Freedom 6
P-Value 0.4688
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 136.38198 0.27276
2 363.61802 0.72724
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 136.38170 0.27276
2 363.61830 0.72724
CLASSIFICATION QUALITY
Entropy 0.904
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 127 0.25400
2 373 0.74600
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.986 0.014
2 0.030 0.970
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Latent Class 1
Thresholds
HM$1 -2.063 0.373 -5.536 0.000
HE$1 -1.724 0.300 -5.755 0.000
VOC$1 2.331 0.389 5.985 0.000
NOCOL$1 2.078 0.320 6.490 0.000
Latent Class 2
Thresholds
HM$1 2.091 0.182 11.502 0.000
HE$1 2.056 0.180 11.401 0.000
VOC$1 -2.187 0.203 -10.760 0.000
NOCOL$1 -1.937 0.183 -10.613 0.000
Categorical Latent Variables
Means
C#1 -0.981 0.116 -8.468 0.000
RESULTS IN PROBABILITY SCALE
Latent Class 1
HM
Category 1 0.113 0.037 3.025 0.002
Category 2 0.887 0.037 23.799 0.000
HE
Category 1 0.151 0.038 3.934 0.000
Category 2 0.849 0.038 22.056 0.000
VOC
Category 1 0.911 0.031 28.987 0.000
Category 2 0.089 0.031 2.817 0.005
NOCOL
Category 1 0.889 0.032 28.072 0.000
Category 2 0.111 0.032 3.514 0.000
Latent Class 2
HM
Category 1 0.890 0.018 50.016 0.000
Category 2 0.110 0.018 6.181 0.000
HE
Category 1 0.887 0.018 48.873 0.000
Category 2 0.113 0.018 6.256 0.000
VOC
Category 1 0.101 0.018 5.472 0.000
Category 2 0.899 0.018 48.748 0.000
NOCOL
Category 1 0.126 0.020 6.267 0.000
Category 2 0.874 0.020 43.498 0.000
LATENT CLASS ODDS RATIO RESULTS
Latent Class 1 Compared to Latent Class 2
HM
Category > 1 63.670 25.875 2.461 0.014
HE
Category > 1 43.795 14.941 2.931 0.003
VOC
Category > 1 0.011 0.005 2.351 0.019
NOCOL
Category > 1 0.018 0.007 2.768 0.006
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.600E-01
(ratio of smallest to largest eigenvalue)
Towards the top of the output, under FINAL CLASS COUNTS…, Mplus gives the final counts and proportions for the classes in several ways. First it gives the counts (i.e. the number of cases in each class) and proportions based on the estimated model, and on the posterior probabilities. This gives the proportion (and count) of individuals estimated to be in each class in the model. Below that, Mplus gives the classification based on most likely class membership, which is an alternative method of assigning individuals to classes. Based on the estimated model and posterior probabilities we see that about 27% of students belong to class 1, and about 73% belong to class 2. Based on most likely class membership, about 25% of students belong to class 1 and the remaining 75% to class 2. Under MODEL RESULTS the thresholds for the classes are listed. Thresholds are on the logit scale, and hence, can be somewhat difficult to interpret. The same information is given in a more interpretable scale under RESULTS IN PROBABILITY SCALE. Here we see that the probability that an individual in class 1 will be in category 2 of the variable hm is .89. In other words, the estimated probability of a student in class 1 taking honors math is about .89.
2.0 Using both categorical and continuous indicator variables
Above we estimated a specific case of a mixture model, a latent class analysis, in which all of the indicators are categorical, in this example the model contains both categorical and continuous indicators. In addition to the four categorical variables used in the example above, this model includes four continuous variables, the students score on a measure of academic achievement for each of the four years of high school (ach9–ach12). The achievement variables have been centered so that each has a mean of zero. The only difference between the input file for this model and the one for the LCA estimated above is that the usevariables option has been dropped because all variables in the dataset are used in the model. In general, the only difference between the input file for a mixture model with all categorical indicators and the input for a model that includes continuous variables is the type of variables included.
Title: Categorical and continuous indicators Data: file is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat; Variable: names are hm he voc nocol ach9-ach12; classes = c (2); categorical = hm he voc nocol ; Analysis: type = mixture;
Below is the output for this model.
*** WARNING in MODEL command
All variables are uncorrelated with all other variables within class.
Check that this is what is intended.
1 WARNING(S) FOUND IN THE INPUT INSTRUCTIONS
Categorical and continuous indicators
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 8
Number of independent variables 0
Number of continuous latent variables 0
Number of categorical latent variables 1
Observed dependent variables
Continuous
ACH9 ACH10 ACH11 ACH12
Binary and ordered categorical (ordinal)
HM HE VOC NOCOL
Categorical latent variables
C
Estimator MLR
Information matrix OBSERVED
Optimization Specifications for the Quasi-Newton Algorithm for
Continuous Outcomes
Maximum number of iterations 100
Convergence criterion 0.100D-05
Optimization Specifications for the EM Algorithm
Maximum number of iterations 500
Convergence criteria
Loglikelihood change 0.100D-06
Relative loglikelihood change 0.100D-06
Derivative 0.100D-05
Optimization Specifications for the M step of the EM Algorithm for
Categorical Latent variables
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Optimization Specifications for the M step of the EM Algorithm for
Censored, Binary or Ordered Categorical (Ordinal), Unordered
Categorical (Nominal) and Count Outcomes
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Maximum value for logit thresholds 15
Minimum value for logit thresholds -15
Minimum expected cell size for chi-square 0.100D-01
Optimization algorithm EMA
Random Starts Specifications
Number of initial stage random starts 10
Number of final stage optimizations 2
Number of initial stage iterations 10
Initial stage convergence criterion 0.100D+01
Random starts scale 0.500D+01
Random seed for generating random starts 0
Link LOGIT
Input data file(s)
https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat
Input data format FREE
SUMMARY OF CATEGORICAL DATA PROPORTIONS
HM
Category 1 0.678
Category 2 0.322
HE
Category 1 0.686
Category 2 0.314
VOC
Category 1 0.322
Category 2 0.678
NOCOL
Category 1 0.334
Category 2 0.666
RANDOM STARTS RESULTS RANKED FROM THE BEST TO THE WORST LOGLIKELIHOOD VALUES
Final stage loglikelihood values at local maxima, seeds, and initial stage start numbers:
-3842.353 unperturbed 0
-3842.353 462953 7
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -3842.353
H0 Scaling Correction Factor 0.982
for MLR
Information Criteria
Number of Free Parameters 21
Akaike (AIC) 7726.706
Bayesian (BIC) 7815.213
Sample-Size Adjusted BIC 7748.557
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit for the Binary and Ordered Categorical
(Ordinal) Outcomes
Pearson Chi-Square
Value 7.628
Degrees of Freedom 6
P-Value 0.2666
Likelihood Ratio Chi-Square
Value 6.974
Degrees of Freedom 6
P-Value 0.3233
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 367.56581 0.73513
2 132.43419 0.26487
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 367.56581 0.73513
2 132.43419 0.26487
CLASSIFICATION QUALITY
Entropy 0.998
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 368 0.73600
2 132 0.26400
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.999 0.001
2 0.000 1.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Latent Class 1
Means
ACH9 -2.058 0.055 -37.121 0.000
ACH10 -2.061 0.051 -40.656 0.000
ACH11 -0.987 0.055 -18.070 0.000
ACH12 -0.990 0.052 -19.023 0.000
Thresholds
HM$1 2.021 0.162 12.453 0.000
HE$1 2.075 0.166 12.521 0.000
VOC$1 -2.075 0.166 -12.525 0.000
NOCOL$1 -1.931 0.157 -12.280 0.000
Variances
ACH9 1.116 0.073 15.346 0.000
ACH10 0.956 0.058 16.601 0.000
ACH11 1.031 0.059 17.382 0.000
ACH12 0.946 0.060 15.727 0.000
Latent Class 2
Means
ACH9 1.988 0.091 21.870 0.000
ACH10 1.971 0.087 22.653 0.000
ACH11 0.987 0.081 12.248 0.000
ACH12 0.829 0.080 10.425 0.000
Thresholds
HM$1 -2.101 0.282 -7.440 0.000
HE$1 -1.954 0.266 -7.354 0.000
VOC$1 2.267 0.302 7.514 0.000
NOCOL$1 2.306 0.303 7.617 0.000
Variances
ACH9 1.116 0.073 15.346 0.000
ACH10 0.956 0.058 16.601 0.000
ACH11 1.031 0.059 17.382 0.000
ACH12 0.946 0.060 15.727 0.000
Categorical Latent Variables
Means
C#1 1.021 0.102 10.055 0.000
RESULTS IN PROBABILITY SCALE
Latent Class 1
HM
Category 1 0.883 0.017 52.665 0.000
Category 2 0.117 0.017 6.977 0.000
HE
Category 1 0.888 0.016 54.096 0.000
Category 2 0.112 0.016 6.792 0.000
VOC
Category 1 0.112 0.016 6.794 0.000
Category 2 0.888 0.016 54.114 0.000
NOCOL
Category 1 0.127 0.017 7.283 0.000
Category 2 0.873 0.017 50.207 0.000
Latent Class 2
HM
Category 1 0.109 0.027 3.974 0.000
Category 2 0.891 0.027 32.487 0.000
HE
Category 1 0.124 0.029 4.296 0.000
Category 2 0.876 0.029 30.323 0.000
VOC
Category 1 0.906 0.026 35.304 0.000
Category 2 0.094 0.026 3.658 0.000
NOCOL
Category 1 0.909 0.025 36.451 0.000
Category 2 0.091 0.025 3.632 0.000
LATENT CLASS ODDS RATIO RESULTS
Latent Class 1 Compared to Latent Class 2
HM
Category > 1 0.016 0.005 3.066 0.002
HE
Category > 1 0.018 0.006 3.188 0.001
VOC
Category > 1 76.870 26.448 2.906 0.004
NOCOL
Category > 1 69.181 23.612 2.930 0.003
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.275E-01
(ratio of smallest to largest eigenvalue)
Towards the top of the output is a message warning us that all of the variables are uncorrelated within clusters. This “warning” does not imply a problem with the model, it is merely there to remind the user that the restriction exists, whether this restriction is appropriate must be determined by the user. In addition to the thresholds for the categorical items (which were included in the output for the previous example), the output for this model includes means and variances for the continuous indicators (i.e. ach9–ach12). The means for the academic achievement variables (ach9–ach12) are all lower in the first class than the second class. The first class is also less likely to have taken honors classes (hm and he) and more likely to have taken vocational classes (voc) and to say they don’t intend to go to college (nocol). Although the order of the classes has reversed (i.e. the class we have called "academically oriented students" is class 2 in this model) the results of this model are consistent with the results from the model in the first example. The models in both examples are consistent with hypothesis that there are two types of students, those who are academically oriented, and those who are not. Note that by default, Mplus specifies the model so that it assumes the variances of the continuous class indicators (ach9–ach12) are equal across all classes, this assumption may or may not be appropriate.
3.0 Saving Class Assignments
In addition to the output file produced by Mplus, it is possible to save class membership information for each case in the dataset to a text file. This text file can later be used with Mplus or read into another statistical package. To do this the savedata: command is added to the input file. The file option gives the name of the file in which the class assignments should be saved (i.e. class.txt). Whenever the file option is used, all of the variables used in the analysis are saved in an external file. The save = cprob; option specifies that the class probabilities should be saved, in addition to the variables used in estimation. Additional variables that were not used in the analysis, but which you wish to include in the saved file, for example, an id variable, can be included by adding the auxiliary option (e.g. auxiliary = id;) to the variable: command.
Title: Saving class probabilities Data: file is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat; Variable: names are hm he voc nocol ach9-ach12; usevariables are hm he voc nocol ; classes = c (2); categorical = hm he voc nocol ; Analysis: type = mixture; Savedata: file is class.txt; save = cprob;
The output file for this model contains all of the information contained in the output for the model in the first example, plus additional output associated with the savedata: command. This additional output appears towards the end of the output file, and is shown below.
SAVEDATA INFORMATION
Order and format of variables
HM F10.3
HE F10.3
VOC F10.3
NOCOL F10.3
CPROB1 F10.3
CPROB2 F10.3
C F10.3
Save file
class.txt
Save file format
7F10.3
Save file record length 5000
The additional output associated with the savedata: command lists the variables in the order in which they appear in the saved dataset. Note that the 4 observed variables used in estimation are listed first, followed by three variables associated with the latent class assignment. The variables CPROB1 and CPROB2 give the probability that each case is in class 1 or class 2, respectively. The variable C contains the class assignment based on posterior probabilities. Below the list of variables the name of the file, and information on the format of the file are shown.
The file class.txt is a text file that can be read by a large number of programs. The first few lines of this file are shown below. Based on the information in the output file, we know that the first four columns contain each student’s value for the variables hm, hw, voc, and nocol (in that order), the remaining three columns are each student’s predicted probability for each of the two classes, and the final column contains the student’s class membership.
1.000 1.000 0.000 1.000 0.963 0.037 1.000
1.000 0.000 0.000 0.000 0.971 0.029 1.000
0.000 0.000 1.000 1.000 0.000 1.000 2.000
1.000 1.000 0.000 0.000 0.999 0.001 1.000
1.000 1.000 0.000 0.000 0.999 0.001 1.000
4.0 Plots
Plots based on the estimated model can also be requested by adding the plot: command to the input file. The type option specifies the type of plots desired, in this case, plot3 requests all plots available for this model. The series option gives the variables to be included in the plots, this can contain either categorical or continuous variables (but not both at the same time). The list of variables in the series option is followed by (*) this uses the defaults for the scaling of the x-axis in the plots. For more information on scaling of the x-axis see the Mplus manual.
Title: Categorical and continuous indicators Data: file is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lca.dat; Variable: names are hm he voc nocol ach9-ach12; classes = C (2); categorical = hm he voc nocol ; Analysis: type = mixture; Plot: type = plot3; series = ach9-ach12(*);
From the Graph menu select View graphs. Because the variables we wish to plot are continuous, we select Estimated means, for categorical variables we would select Estimated probabilities. The options under View graphs are somewhat limited for this model, if you were to specify a model where class membership was predicted by additional variables, then a larger variety of graphs is available.
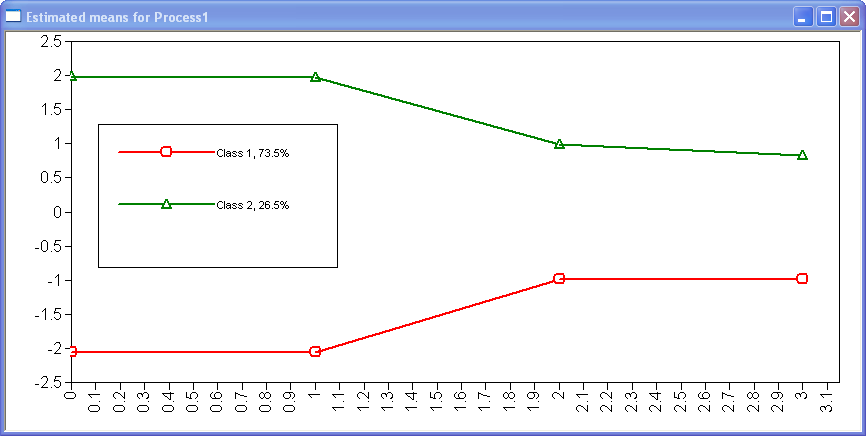
This graph, sometimes called a profile plot, shows graphically the latent class means given in the MODEL RESULTS section of the output for the second example. By default, the x-axis starts at zero and increases in units of one for each of the observed variables. In our example, this means that the means for the variable ach9 shown at 0, followed by ach10 at 1, etc.
The legend tells us that class 1 is shown in red, and class 2 in green. It also gives the proportion of cases in each class, in this case an estimated 26% of students are in class 1, and 74% are in class 2. This information can be found in the output under the heading "Final Class Counts and Proportions for the latent Classes Based on the Estimated Model". Consistent with the means shown in the output for example 2,the plot shows that students in class 1 have lower average scores on all four of the achievement variables (ach9–ach12) than students in class 2.
