Note that this page contains a description of the defaults, other specifications are possible.
For a model with all continuous variables
The short answer
Directly below are lists of which coefficients are fixed and free across groups in a measurement only model. Further below is an example and more detailed explanation.
The following parameters are fixed to equality across groups:
- Factor loadings (denoted “BY” in the output)
- Intercepts of the manifest (a.k.a. observed) variables (listed under “Intercepts” in the output)
The following parameters are allowed to be different across groups:
- Covariances between the latent variables (denoted “WITH”)
- Variances of the latent variables (listed under “Variances”)
- Residual variances of the manifest variables (listed under “Residual Variances”)
The following coefficients are fixed to an arbitrary (but customary) value for identification of the model:
- The first factor loading for each latent variable is set to 1 in all groups.
- The means of latent variables are set to 0 in the first group, and freely estimated in all subsequent groups.
The figure below graphically shows which parameters are fixed, and which are free. Paths that are constrained to equality across groups are shown in blue. Paths and other coefficients that are allowed to differ across groups are shown in red. Paths in black with values next to them are all constrained to one.
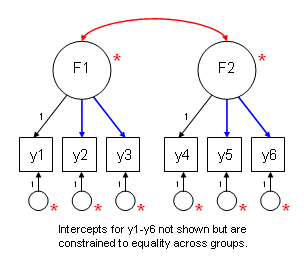
An example with explanation
Below is a two-group model (the groups are males and females), with three latent variables (x1, x2 and x3). All of the observed variables are continuous.
Data:
File is D:datamydata.dat;
Variable:
Names are a1 a2 a3 b1 b2 b3 b4 d1 d2 d3 female;
grouping is female (0 = male 1 = female);
Missing are all (-9999) ;
Analysis:
Type = general ;
Model:
x1 by a1 a2 a3;
x2 by b1 b2 b3 b4;
x3 by d1 d2 d3;
We have edited the output to put the parameter estimates and standard errors for each group next to each other (Mplus prints the output sequentially by group). You can view or download the full, unedited, Mplus output by clicking here. To make it easier to follow along we will examine the output in sections, starting with the factor loadings (indicated with the key word BY).
By default Mplus sets the factor loading for the first manifest variable listed to one in order to identify the model. (This is arbitrary, other values, or manifest variables, and even other methods, can be used to identify the model.) Comparing subsequent factor loadings for each of the latent variables (factors) we can see that both the coefficients, and their standard error are the same. In other words, Mplus has constrained them to equality for males and females by default.
Males Females
Estimate S.E. Estimate S.E.
X1 BY
A1 1.000 0.000 1.000 0.000
A2 0.934 0.023 0.934 0.023
A3 0.771 0.027 0.771 0.027
X2 BY
B1 1.000 0.000 1.000 0.000
B2 1.100 0.068 1.100 0.068
B3 0.075 0.020 0.075 0.020
B4 0.029 0.009 0.029 0.009
X3 BY
D1 1.000 0.000 1.000 0.000
D2 1.014 0.081 1.014 0.081
D3 0.523 0.047 0.523 0.047
Next we will compare the covariances among the latent variables. Here, the estimates are very different. For example, the covariance of X1 with X2 is -0.237 for males and 0.17 for females. Clearly they are not constrained to equality.
Males Females
Estimate S.E. Estimate S.E.
X2 WITH
X1 -0.237 0.222 0.170 0.111
X3 WITH
X1 -0.004 0.038 0.024 0.025
X2 0.119 0.034 0.054 0.019
Looking at the means of the latent variables you probably notice right away that for males, all three latent variables have a mean of zero. In contrast, the estimated means for females are different from zero (although not significantly so in two of the three cases). This is related to identification of the model. Because there is no unique solution for the means of the latent variables, the model estimates the difference between the means of the latent variables by group, (rather than values of the means of the latent variables for each group). In order to estimate the difference in means between groups, the mean for one of the groups is fixed to some arbitrary value, typically zero.
Males Females
Estimate S.E. Estimate S.E.
Means
X1 0.000 0.000 0.084 0.166
X2 0.000 0.000 -0.201 0.131
X3 0.000 0.000 0.010 0.027
Below we see that the intercepts for the observed variables are constrained to equality across groups.
Males Females
Estimate S.E. Estimate S.E.
Intercepts
A1 4.202 0.142 4.202 0.142
A2 4.120 0.135 4.120 0.135
A3 4.348 0.116 4.348 0.116
B1 0.630 0.118 0.630 0.118
B2 0.685 0.128 0.685 0.128
B3 0.172 0.027 0.172 0.027
B4 0.080 0.013 0.080 0.013
D1 0.084 0.020 0.084 0.020
D2 0.069 0.023 0.069 0.023
D3 0.067 0.015 0.067 0.015
Below we see that both the variances of the latent variables and the residual variances of the manifest (observed) variables are allowed to be different across groups.
Males Females
Estimate S.E. Estimate S.E.
Variances
X1 3.481 0.388 3.082 0.219
X2 2.365 0.302 1.511 0.151
X3 0.065 0.009 0.076 0.010
Residual Variances
A1 0.185 0.084 0.027 0.053
A2 0.524 0.091 0.626 0.063
A3 1.094 0.127 1.075 0.081
B1 0.321 0.144 0.362 0.102
B2 0.070 0.172 0.215 0.120
B3 0.496 0.052 0.359 0.025
B4 0.066 0.007 0.107 0.007
D1 0.006 0.005 0.109 0.010
D2 0.034 0.006 0.009 0.007
D3 0.046 0.005 0.072 0.005
For a model with categorical observed variables
The short answer
Directly below are lists of which coefficients are fixed and free across groups. Further below is an example and more detailed explanation.
The following parameters are fixed to equality across groups:
- Factor loadings (denoted “BY”)
- Thresholds (listed under “Thresholds”)
The following parameters are allowed to be different across groups:
- Covariances between the latent variables (denoted “WITH”)
- Variances of the latent variables (listed under “Variances”)
The following coefficients are fixed to an arbitrary (but customary) value for identification of the model:
- The first factor loading for each latent variable is set to 1 in all groups.
- The mean of latent variables are set to 0 in the first group, and freely estimated in all subsequent groups.
- The scales are constrained to one in the first group, and freely estimated in all subsequent groups.
An example with explanation
Below is a two-group model (the groups are males and females), with two latent variables (x1 and x2). In this model, all of the observed variables are dichotomous.
Data:
File is D:\data\mydata.dat ;
Variable:
Names are
a1d a2d a3d b1d b2d b3d female;
Missing are all (-9999) ;
categorical are a1d a2d a3d b1d b2d b3d ;
grouping is female (0 = male 1 = female);
Analysis:
Type = general ;
Model:
x1 by a1d a2d a3d;
x2 by b1d b2d b3d;
We have edited the output to put the parameter estimates and standard errors for each group next to each other (Mplus prints the output sequentially by group). You can view or download the full, unedited Mplus output by clicking here. To make it easier to follow along we will examine the output in sections, starting with the factor loadings (indicated with the key word BY). By default Mplus sets the factor loading for the first manifest variable listed to one in order to identify the model. (This is arbitrary, other loadings, manifest variables, and even other methods, can be used to identify the model.) Comparing subsequent factor loadings for each of the latent variables (factors) we can see that both the coefficients, and their standard error are the same. In other words, Mplus has constrained them to equality for males and females by default. (It is very unlikely that the model would produce identical estimates unless the coefficients were constrained to equality across groups.)
Male Female
Estimate S.E. Estimate S.E.
X1 BY
A1D 1.000 0.000 1.000 0.000
A2D 0.757 0.255 0.757 0.255
A3D 1.345 0.601 1.345 0.601
X2 BY
B1D 1.000 0.000 1.000 0.000
B2D 0.857 0.083 0.857 0.083
B3D 0.860 0.086 0.860 0.086
Next we will compare the covariances among the latent variables. Here, the estimates are very different in the two groups. The covariance of X2 with X1 is -0.113 for males and -0.081 for females. Clearly they are not constrained to equality.
Male Female
Estimate S.E. Estimate S.E.
X2 WITH
X1 -0.113 0.057 -0.081 0.064
Looking at the means of the latent variables you probably notice right away that for males, both latent variables have a mean of zero. In contrast the estimated means for females are different from zero (although the difference is not statistically significant in this case). This is related to identification of the model. Instead of estimating the actual mean for each group, the difference between the groups is estimated. To do this the mean for one of the groups is fixed to some arbitrary value, typically zero.
Male Female
Estimate S.E. Estimate S.E.
Means
X1 0.000 0.000 -0.467 0.167
X2 0.000 0.000 0.486 0.891
For categorical observed variables Mplus gives thresholds of the observed variables rather than intercepts (Threshold = -1 * intercept). Like the intercepts of the observed variables in the continuous example above, the thresholds are constrained to equality across groups.
Male Female
Estimate S.E. Estimate S.E.
Thresholds
A1D$1 1.608 0.073 1.608 0.073
A2D$1 -0.232 0.045 -0.232 0.045
A3D$1 0.261 0.045 0.261 0.045
B1D$1 -1.153 0.056 -1.153 0.056
B2D$1 -0.880 0.050 -0.880 0.050
B3D$1 -1.338 0.062 -1.338 0.062
Below we see that the variances of the latent variables are allowed to be different across groups.
Male Female
Estimate S.E. Estimate S.E.
Variances
X1 0.238 0.137 0.195 0.136
X2 0.748 0.088 1.051 1.139
Similar to the means of the latent variables, the scales are fixed in the first group (although to one in this case), and estimated in the second group. For categorical observed variables, the scale factors relate to the variance of the continuous latent response variable underlying the observed values (which are categorical). The scale factor is fixed to one rather than zero because scale coefficients are multiplicative, rather than additive. Fixing the scales to one in one group, and estimating them the other groups allows the variance of the latent response variable to be different across groups.
Male Female
Estimate S.E. Estimate S.E.
Scales
A1D 1.000 0.000 1.031 0.109
A2D 1.000 0.000 1.102 0.726
A3D 1.000 0.000 1.122 0.401
B1D 1.000 0.000 0.813 0.442
B2D 1.000 0.000 0.919 0.535
B3D 1.000 0.000 0.875 0.392
