Mplus will compute standardized coefficients for models with categorical and count dependent variables. Because the variance (and hence the standard deviation) of categorical and count variables is not well defined, calculating standardized coefficients for these models is not as straightforward as calculating standardized coefficients for an OLS regression (i.e. a regression with a continuous dependent variable). As a review, in an OLS model, the formula for the predicted y (y-hat) is:
![]()
and the standardized coefficients (b*) are computed:
![]()
where sx is the standard deviation of the x variable, and sy is the standard deviation of the y variable.
In contrast, for a poisson regression model, we don’t model the dependent variable directly as is done in OLS, instead, we model the natural log of the count, giving the prediction equation:
![]()
To calculate the standardized coefficient shown in the column labeled StdYX (see Mplus output below) Mplus uses the standard deviation of the independent variable, along with the standard deviation of the linear prediction of y (generally denoted xb). Thus the formula for the standardized coefficients (b*) is:
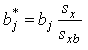
where sx is the standard deviation of the x variable, and sxb is the standard deviation of the linear predictions. It is worth noting that this is not the only possible way of computing a standardized coefficient for a categorical or count model, it is simply the method used by Mplus.
The following example shows the output in Mplus, as well as how to reproduce it using Stata. For this example we will use the same dataset we used for our poisson regression data analysis example. You can download the dataset for Mplus here: poissonreg.dat. The model we specify for this example includes four variables, three predictors and one outcome. We use students gender (male), the student’s score on a standardized test in math (math), and the student’s score on a standardized test in language arts (langarts) to predict the number of days a student was absent from school during a single school year (daysabs). The Mplus input for this model is:
DATA:
File is "D:datapoissonreg.dat" ;
VARIABLE:
Names are id school male math langarts daysatt daysabs;
usevariables are langarts math daysabs male;
count is daysabs;
MODEL:
daysabs on male math langarts;
OUTPUT: stand
Below are the results from the model described above. Note that Mplus produces two types of standardized coefficients “Std” which are in the fifth column of the output shown below, and “StdXY” which are in the sixth column. The Std column contains coefficients standardized using the variance of continuous latent variables. Because all of the variables in this model are manifest (i.e. observed) the coefficients in this column are identical to those in the column of regular coefficients (i.e. the "Estimates" column). The StdXY column contains the coefficients standardized using the variance of the background and/or outcome variables, in addition to the variance of continuous latent variables.
MODEL RESULTS
Estimates S.E. Est./S.E. Std StdYX
DAYSABS ON
MALE -0.401 0.139 -2.877 -0.401 -0.652
MATH -0.004 0.008 -0.462 -0.004 -0.205
LANGARTS -0.012 0.005 -2.299 -0.012 -0.709
Intercepts
DAYSABS 2.688 0.218 12.340 2.688 8.750
Now, we will replicate these coefficients in Stata. The first bold line below opens the dataset, and the second runs the poisson regression model in Stata. Note that the unstandardized coefficients from Stata and Mplus are within rounding error of eachother, this should be the case, since we are running the same model.
use https://stats.idre.ucla.edu/stat/stata/dae/poissonreg, clear
poisson daysabs male math langarts
Iteration 0: log likelihood = -1547.9709
Iteration 1: log likelihood = -1547.9709
Poisson regression Number of obs = 316
LR chi2(3) = 175.27
Prob > chi2 = 0.0000
Log likelihood = -1547.9709 Pseudo R2 = 0.0536
------------------------------------------------------------------------------
daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
male | -.4009209 .0484122 -8.28 0.000 -.495807 -.3060348
math | -.0035232 .0018213 -1.93 0.053 -.007093 .0000466
langarts | -.0121521 .0018348 -6.62 0.000 -.0157483 -.0085559
_cons | 2.687666 .0726512 36.99 0.000 2.545272 2.83006
------------------------------------------------------------------------------
In order to calculate a standardized coefficient we will need three pieces of information, the standard deviation of xb (the linear prediction), the standard deviation of the predictor variable for which we want to create a standardized coefficient, and the unstandardized coefficient for that predictor variable. To obtain the standard deviation for the linear predictor, we first use the predict command to generate a new variable called XB which contains the linear prediction (i.e. xb = log(y-hat)) for each case in the dataset, this is done in the first line of syntax below. The predict command can be used to generate various types of predictions after a regression in Stata, specifying xb after the comma tells Stata that the variable XB should contain linear predictions. (Note, the results of the predict command will always be for the last regression command you ran.) Next we summarize the new variable XB, and use Stata’s saved results to place its standard deviation into a local macro called "ystd" using the command local ystd=r(sd). Next we summarize the predictor variable for which we want to create a standardized coefficient, in this case male, and use the results that Stata saves after a command is run to place it’s standard deviation into a local macro called “xstd.” Since Stata automatically stores the coefficients from the last regression we ran, we can access the coefficient for male by typing _b[male]. Now we are ready to actually calculate the standardized coefficients. The second to last command below creates a new local macro called "male_std" and sets it equal to the standardized coefficient for male (i.e. _b[male]*`xstd’/`ystd’). The last command shown below tells Stata to display the contents of "male_std" which is the standardized coefficient for the relationship between male and log of the predicted count of daysabs. This value is approximately -0.652, looking at the Mplus output above, we see that the standardized coefficient (StdYX) for male is also estimated to be -0.652 by Mplus.
predict XB, xb sum XB Variable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- xb | 316 1.712138 .3076592 .8868849 2.671879 local ystd=r(sd) sum male Variable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- male | 316 .4873418 .5006325 0 1 local xstd = r(sd)local male_std = _b[male]*`xstd'/`ystd' display "`male_std'" -.6523909465586064
The commands and output below show the same process for the other two predictor variables in the model.
sum math
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
math | 316 48.75101 17.88076 1.007114 98.99289
local xstd = r(sd)
local math_std = _b[math]*`xstd'/`ystd'
display "`math_std'"
-.2047650322590808
sum langarts
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
langarts | 316 50.06379 17.93921 1.007114 98.99289
local xstd = r(sd)
local langarts_std = _b[langarts]*`xstd'/`ystd'
display "`langarts_std'"
-.7085747822838703
Cautions, Flies in the Ointment
- Because the variance of the linear prediction (xb) is used instead of the actual variance of y, your standardized coefficients will be heavily influenced by your model, not just through regression coefficients themselves (which are always based on the model) but through the standardization process as well. This makes the interpretation of these standardized coefficients not as straightforward as standardized coefficients from a linear regression.
See Also
- Mplus User’s Guide
online (See page 503 of the Version 4.1 User’s Guide. Note: this is a free download.)
