Version info: Code for this page was tested in Mplus version 6.12.
Negative binomial regression is used to model count variables with overdispersion.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of negative binomial regression
Example 1. School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include the type of program in which the student is enrolled and a standardized test in math.
Example 2. A health-related researcher is studying the number of hospital visits in past 12 months by senior citizens in a community based on the characteristics of the individuals and the types of health plans under which each one is covered.
Description of the data
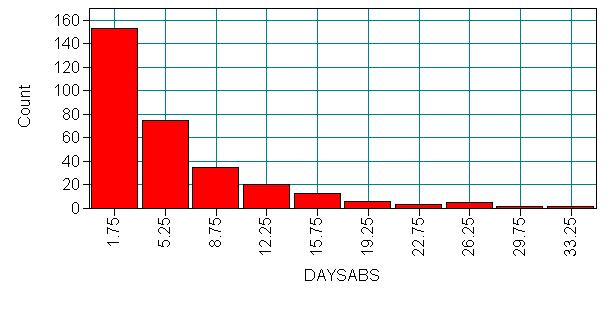
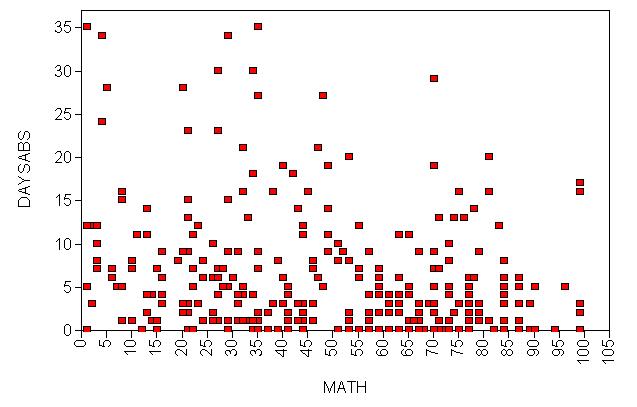
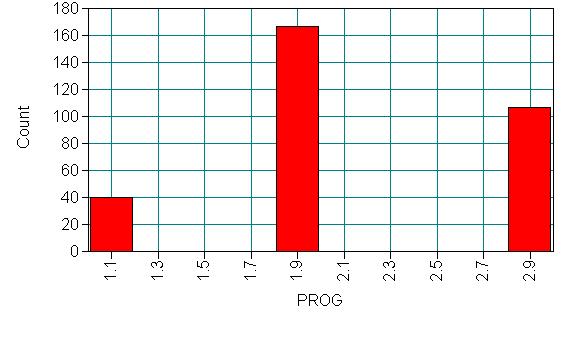
We have attendance data on 314 high school juniors from two urban high schools in the file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.dat. The response variable of interest is days absent, daysabs. The variable math gives the standardized math score for each student. The variable prog is a three-level nominal variable indicating the type of instructional program in which the student is enrolled. The variables p1, p2 and p3 are dummy-coded indicator variables for prog.
Let’s look at the data. It is always a good idea to start with descriptive statistics.
Data: File is g:daehttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.dat; Variable: Names are id gender math daysabs prog p1 p2 p3; Missing are all (-9999); usevariables are id gender math daysabs prog p1 p2 p3; analysis: type = basic; plot: type is plot1;
RESULTS FOR BASIC ANALYSIS
ESTIMATED SAMPLE STATISTICS
Means
ID GENDER MATH DAYSABS PROG
________ ________ ________ ________ ________
1 1575.911 1.490 48.268 5.955 2.213
Means
P1 P2 P3
________ ________ ________
1 0.127 0.532 0.341
Covariances
ID GENDER MATH DAYSABS PROG
________ ________ ________ ________ ________
ID 251516.623
GENDER -27.319 0.250
MATH 4840.852 -0.227 641.202
DAYSABS -1193.221 -0.357 -41.966 49.361
PROG 165.742 0.004 3.895 -1.717 0.423
P1 -17.479 -0.005 -0.439 0.598 -0.155
P2 -130.784 0.007 -3.018 0.521 -0.113
P3 148.263 -0.002 3.457 -1.119 0.268
Covariances
P1 P2 P3
________ ________ ________
P1 0.111
P2 -0.068 0.249
P3 -0.043 -0.181 0.225
Correlations
ID GENDER MATH DAYSABS PROG
________ ________ ________ ________ ________
ID 1.000
GENDER -0.109 1.000
MATH 0.381 -0.018 1.000
DAYSABS -0.339 -0.102 -0.236 1.000
PROG 0.508 0.011 0.237 -0.376 1.000
P1 -0.105 -0.031 -0.052 0.255 -0.713
P2 -0.523 0.027 -0.239 0.148 -0.350
P3 0.624 -0.006 0.288 -0.336 0.870
Correlations
P1 P2 P3
________ ________ ________
P1 1.000
P2 -0.407 1.000
P3 -0.275 -0.766 1.000
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Negative binomial regression -Negative binomial regression can be used for over-dispersed count data, that is when the conditional variance exceeds the conditional mean. It can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression and it has an extra parameter to model the over-dispersion. If the conditional distribution of the outcome variable is over-dispersed, the confidence intervals for the Negative binomial regression are likely to be narrower as compared to those from a Poisson regression model.
- Poisson regression – Poisson regression is often used for modeling count data. Poisson regression has a number of extensions useful for count models.
- Zero-inflated regression model – Zero-inflated models attempt to account for excess zeros. In other words, two kinds of zeros are thought to exist in the data, "true zeros" and "excess zeros". Zero-inflated models estimate two equations simultaneously, one for the count model and one for the excess zeros.
- OLS regression – Count outcome variables are sometimes log-transformed and analyzed using OLS regression. Many issues arise with this approach, including loss of data due to undefined values generated by taking the log of zero (which is undefined), as well as the lack of capacity to model the dispersion.
Negative binomial regression analysis
In the Mplus syntax below, we specify that the variables to be used in the negative binomial regression are daysabs, math, p2, p3, which will make prog=1 the reference group. We also specify that daysabs is a count variable, and we include (nb) to indicate that we want a negative binomial regression. (By default, Mplus would model this as a Poisson regression.) By default, Mplus uses restricted maximum likelihood (MLR), so robust standard errors would be given in the output. Here, the standard errors are calculated using maximum likelihood estimates by including the analysis: estimator = ml; block.
Data:
File is g:daehttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.dat;
Variable:
Names are
id gender math daysabs prog p1 p2 p3;
Missing are all (-9999);
usevariables are daysabs math p2 p3;
count is daysabs (nb);
model:
daysabs on math p2 p3;
analysis: estimator = ml;
MODEL FIT INFORMATION
Number of Free Parameters 5
Loglikelihood
H0 Value -865.629
Information Criteria
Akaike (AIC) 1741.258
Bayesian (BIC) 1760.005
Sample-Size Adjusted BIC 1744.146
(n* = (n + 2) / 24)
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
DAYSABS ON
MATH -0.006 0.003 -2.390 0.017
P2 -0.441 0.183 -2.414 0.016
P3 -1.279 0.202 -6.331 0.000
Intercepts
DAYSABS 2.615 0.196 13.319 0.000
Dispersion
DAYSABS 0.968 0.100 9.729 0.000
- After the heading informing that "THE MODEL ESTIMATION TERMINATED NORMALLY" comes the information about the model. It begins with the information regarding the log likelihood, AIC and BIC. These can be used in comparing models.
- Then we will find the negative binomial regression coefficients for each of the variables along with the standard errors. The column labeled as Est./S.E. is the quotient of the estimates divided by the standard errors. These are basically z-scores if the sample size is reasonably large. In the right-most column is the two-tailed p-value.
- The variable math has a coefficient of -0.006, which is statistically significant. This means that for each one-unit increase on math, the expected log count of the number of days absent decreases by 0.006 day. Both of the dummy variables for the variable prog are statistically significant. Compared to level 1 of prog, the expected log count for level 2 decreases by 0.441. Compared to level 1 of prog, the expected log count of for level 3 decreases by 1.279.
- Additionally, under "Dispersion" we find the estimate of the natural log of the over-dispersion coefficient, alpha. If the alpha coefficient is zero then the model is better estimated using a Poisson regression model. Here it is different from zero, so negative binomial regression is appropriate.
To determine if prog itself is statistically significant, we can use the model test block to obtain the two degree-of-freedom test of this variable. Additionally, we can get an estimate of the natural log of the over-dispersion coefficient, alpha. If the alpha coefficient is zero then the model is better estimated using a Poisson regression model.
Data: File is g:daehttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.dat; Variable: Names are id gender math daysabs prog p1 p2 p3; Missing are all (-9999); usevariables are daysabs math p2 p3; count is daysabs (nb); model: daysabs on math (a1) p2 (a2) p3 (a3); model test: a2 = 0; a3 = 0; analysis: estimator = ml;MODEL FIT INFORMATION<**SOME OUTPUT OMITTED**> Wald Test of Parameter Constraints Value 49.214 Degrees of Freedom 2 P-Value 0.0000
In the syntax above, some of the variables in the model are given labels. These labels must be in parentheses and must be the last item listed on the line, so the model is broken up over several lines. We have given the label a2 to the indicator variable p2, and the label a3 to the indicator variable p3. Once we have assigned labels to the variables, we can use those labels in the model test block. Setting both a2 and a3 to 0 allows us to get the two degree-of-freedom test of the variable prog. We can see that the variable prog, as a whole, is statistically significant.
To obtain the results as incident rate ratios, we need to use the model constraint block. Again, we use labels to refer to the variables in the model. In the model constraint block, we use the new statement to label the new parameters, which will be the exponentiated parameters from the model.
Data:
File is g:daehttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/nb_data.dat;
Variable:
Names are
id gender math daysabs prog p1 p2 p3;
Missing are all (-9999);
usevariables are daysabs math p2 p3;
count is daysabs (nb);
model:
daysabs on
math (a1)
p2 (a2)
p3 (a3);
model constraint:
new( math_exp p2_exp p3_exp);
math_exp = exp(a1);
p2_exp = exp(a2);
p3_exp = exp(a3);
analysis: estimator = ml;
MODEL FIT INFORMATION
Number of Free Parameters 5
Loglikelihood
H0 Value -865.629
Information Criteria
Akaike (AIC) 1741.258
Bayesian (BIC) 1760.005
Sample-Size Adjusted BIC 1744.146
(n* = (n + 2) / 24)
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
DAYSABS ON
MATH -0.006 0.003 -2.390 0.017
P2 -0.441 0.183 -2.414 0.016
P3 -1.279 0.202 -6.331 0.000
Intercepts
DAYSABS 2.615 0.196 13.319 0.000
Dispersion
DAYSABS 0.968 0.100 9.729 0.000
New/Additional Parameters
MATH_EXP 0.994 0.002 398.851 0.000
P2_EXP 0.644 0.117 5.477 0.000
P3_EXP 0.278 0.056 4.951 0.000
Things to consider
- It is not recommended that negative binomial models be applied to small samples.
- One common cause of over-dispersion is excess zeros by an additional data generating process. If more than one process generates the data, then it is possible to have more 0s than expected by the negative binomial model; in this case, a zero-inflated model (either zero-inflated Poisson or zero-inflated negative binomial) may be more appropriate.
- If the data generating process does not allow for any 0s (such as the number of days spent in the hospital), then a zero-truncated model may be more appropriate.
- Count data often have an exposure variable, which indicates the number of times the event could have happened. This variable can be incorporated into your negative binomial model by taking the log of the exposure variable and constraining its estimate to 1.
- The outcome variable in a negative binomial regression cannot have negative numbers, and the exposure cannot have 0s.
- Pseudo-R-squared: Many different measures of pseudo-R-squared exist. They all attempt to provide information similar to that provided by R-squared in OLS regression; however, none of them can be interpreted exactly as R-squared in OLS regression is interpreted. For a discussion of various pseudo-R-squares, see Long and Freese (2006) or our FAQ page What are pseudo R-squareds? .
See also
References
- Long, J. S. 1997. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
- Long, J. S. and Freese, J. 2006. Regression Models for Categorical Dependent Variables Using Stata, Second Edition. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. 2009. Microeconometrics Using Stata. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. 1998. Regression Analysis of Count Data. New York: Cambridge Press.
- Cameron, A. C. Advances in Count Data Regression Talk for the Applied Statistics Workshop, March 28, 2009. http://cameron.econ.ucdavis.edu/racd/count.html .
- Dupont, W. D. 2002. Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data. New York: Cambridge Press.