The ttest command performs t-tests for one sample, two samples and paired observations. The single-sample t-test compares the mean of the sample to a given number (which you supply). The independent samples t-test compares the difference in the means from the two groups to a given value (usually 0). In other words, it tests whether the difference in the means is 0. The dependent-sample or paired t-test compares the difference in the means from the two variables measured on the same set of subjects to a given number (usually 0), while taking into account the fact that the scores are not independent. In our examples, we will use the hsb2 data set.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear (highschool and beyond (200 cases))
Single sample t-test
The single sample t-test tests the null hypothesis that the population mean is equal to the given number specified using the option write == . For this example, we will compare the mean of the variable write with a pre-selected value of 50. In practice, the value against which the mean is compared should be based on theoretical considerations and/or previous research. Stata calculates the t-statistic and its p-value under the assumption that the sample comes from an approximately normal distribution. If the p-value associated with the t-test is small (0.05 is often used as the threshold), there is evidence that the mean is different from the hypothesized value. If the p-value associated with the t-test is not small (p > 0.05), then the null hypothesis is not rejected and you can conclude that the mean is not different from the hypothesized value.
In this example, the t-statistic is 4.1403 with 199 degrees of freedom. The corresponding two-tailed p-value is .0001, which is less than 0.05. We conclude that the mean of variable write is different from 50.
ttest write==50
One-sample t test
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
write | 200 52.775 .6702372 9.478586 51.45332 54.09668
------------------------------------------------------------------------------
mean = mean(write) t = 4.1403
Ho: mean = 50 degrees of freedom = 199
Ha: mean < 50 Ha: mean != 50 Ha: mean > 50
Pr(T < t) = 1.0000 Pr(|T| > |t|) = 0.0001 Pr(T > t) = 0.0000
Summary Statistics
---------------------------------------------------------------------------------- Variablea | Obsb Meanc Std. Err.d Std. Dev.e [95% Conf. Interval]f ----------+----------------------------------------------------------------------- write | 200 52.775 .6702372 9.478586 51.45332 54.09668 ----------------------------------------------------------------------------------
a.Variable – This is the variable for which the test was conducted.
b.Obs – The number of valid (i.e., non-missing) observations used in calculating the t-test.
c. Mean – This is the mean of the variable.
d. Std. Err. – This is the estimated standard deviation of the sample mean. If we drew repeated samples of size 200, we would expect the standard deviation of the sample means to be close to the standard error. The standard deviation of the distribution of sample mean is estimated as the standard deviation of the sample divided by the square root of sample size: 9.478586/(sqrt(200)) = .6702372.
e. Std. Dev. – This is the standard deviation of the variable.
f. 95% Confidence Interval – These are the lower and upper bound of the confidence interval for the mean. A confidence interval for the mean specifies a range of values within which the unknown population parameter, in this case the mean, may lie. It is given by
![]()
where s is the sample deviation of the observations and N is the number of valid observations. The t-value in the formula can be computed or found in any statistics book with the degrees of freedom being N-1 and the p-value being 1-alpha/2, where alpha is the confidence level and by default is .95.
Test Statistics
meang = mean(write) th = 4.1403 Hoi: mean = 50 degrees of freedomj = 199 Ha: mean < 50 Ha: mean != 50 Ha: mean > 50 Pr(T < t)k = 1.0000 Pr(|T| > |t|)l = 0.0001 Pr(T > t)k = 0.0000
g. mean – This is the mean being tested. In this example it is the mean of write.
h. t – This is the Student t-statistic. It is the ratio of the difference between the sample mean and the given number to the standard error of the mean: (52.775 – 50) / .6702372 = 4.1403. Since the standard error of the mean measures the variability of the sample mean, the smaller the standard error of the mean, the more likely that our sample mean is close to the true population mean. This is illustrated by the following three figures.
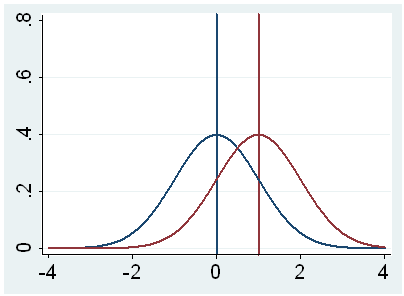
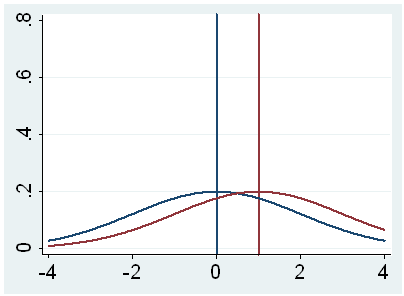
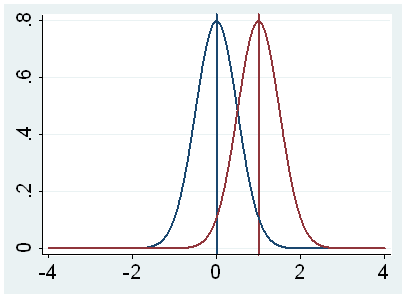
In all three cases, the difference between the population means is the same. But with large variability of sample means, second graph, two populations overlap a great deal. Therefore, the difference may well come by chance. On the other hand, with small variability, the difference is more clear as in the third graph. The smaller the standard error of the mean, the larger the magnitude of the t-value and therefore, the smaller the p-value.
i. Ho – This is the null hypothesis that is being tested. The single sample t-test evaluates the null hypothesis that the population mean is equal to the given number.
j. degrees of freedom – The degrees of freedom for the single sample t-test is simply the number of valid observations minus 1. We lose one degree of freedom because we have estimated the mean from the sample. We have used some of the information from the data to estimate the mean, therefore it is not available to use for the test and the degrees of freedom accounts for this.
k. Pr(T < t), Pr(T > t) – These are the one-tailed p-values evaluating the null against the alternatives that the mean is less than 50 (left test) and greater than 50 (right test). These probabilities are computed using the t distribution. Again, if p-value is less than the pre-specified alpha level (usually .05 or .01) we will conclude that mean is statistically significantly greater or less than the null hypothetical value.
l. Pr(|T| > |t|) – This is the two-tailed p-value evaluating the null against an alternative that the mean is not equal to 50. It is equal to the probability of observing a greater absolute value of t under the null hypothesis. If p-value is less than the pre-specified alpha level (usually .05 or .01, here the former) we will conclude that mean is statistically significantly different from zero. For example, the p-value for write is smaller than 0.05. So we conclude that the mean for write is different from 50.
Paired t-test
A paired (or “dependent”) t-test is used when the observations are not independent of one another. In the example below, the same students took both the writing and the reading test. Hence, you would expect there to be a relationship between the scores provided by each student. The paired t-test accounts for this. For each student, we are essentially looking at the differences in the values of the two variables and testing if the mean of these differences is equal to zero.
In this example, the t-statistic is 0.8673 with 199 degrees of freedom. The corresponding two-tailed p-value is 0.3868, which is greater than 0.05. We conclude that the mean difference of write and read is not different from 0.
ttest write==read
Paired t test
------------------------------------------------------------------------------
Variable | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
write | 200 52.775 .6702372 9.478586 51.45332 54.09668
read | 200 52.23 .7249921 10.25294 50.80035 53.65965
---------+--------------------------------------------------------------------
diff | 200 .545 .6283822 8.886666 -.6941424 1.784142
------------------------------------------------------------------------------
mean(diff) = mean(write - read) t = 0.8673
Ho: mean(diff) = 0 degrees of freedom = 199
Ha: mean(diff) < 0 Ha: mean(diff) != 0 Ha: mean(diff) > 0
Pr(T < t) = 0.8066 Pr(|T| > |t|) = 0.3868 Pr(T > t) = 0.1934
Summary Statistics
---------------------------------------------------------------------------------- Variablea | Obsb Meanc Std. Err.d Std. Dev.e [95% Conf. Interval]f ----------+----------------------------------------------------------------------- write | 200 52.775 .6702372 9.478586 51.45332 54.09668 read | 200 52.23 .7249921 10.25294 50.80035 53.65965 ----------+----------------------------------------------------------------------- diff | 200 .545 .6283822 8.886666 -.6941424 1.784142 ----------------------------------------------------------------------------------
a.Variable – This is the list of variables used in the test.
b.Obs – The number of valid (i.e., non-missing) observations used in calculating the t-test.
c. Mean – This is the list of the means of the variables. The last row displays the simple difference between the two means.
d. Std. Err. – This is the estimated standard deviation of the sample mean. If we drew repeated samples of size 200, we would expect the standard deviation of the sample means to be close to the standard error. The standard deviation of the distribution of sample mean is estimated as the standard deviation of the sample divided by the square root of sample size. This provides a measure of the variability of the sample mean. The Central Limit Theorem tells us that the sample means are approximately normally distributed when the sample size is 30 or greater.
e. Std. Dev. – This is the standard deviation of the variable. The last row displays the standard deviation for the difference which is not equal to the difference of standard deviations for each group.
f. 95% Confidence Interval – These are the lower and upper bound of the confidence interval for the mean. A confidence interval for the mean specifies a range of values within which the unknown population parameter, in this case the mean, may lie. It is given by
![]()
where s is the sample deviation of the observations and N is the number of valid observations. The t-value in the formula can be computed or found in any statistics book with the degrees of freedom being N-1 and the p-value being 1-alpha/2, where alpha is the confidence level and by default is .95.
Test Statistics
mean(diff) = mean(write – read)g t = 0.8673h Ho: mean(diff) = 0 degrees of freedom = 199i
Ha: mean(diff) < 0k Ha: mean(diff) != 0j Ha: mean(diff) > 0k Pr(T < t) = 0.8066 Pr(|T| > |t|) = 0.3868 Pr(T > t) = 0.1934
g. mean(diff) = mean(var1 – var2)– The t-test for dependent groups forms a single random sample from the paired difference, which functions as a simple random sample test. The interpretation for t-value and p-value is the same as in the case of simple random sample.
h. t – This is the t-statistic. It is the ratio of the mean of the difference to the standard error of the difference (.545/.6283822).
i. degrees of freedom – The degrees of freedom for the paired observations is simply the number of observations minus 1. This is because the test is conducted on the one sample of the paired differences.
j. Pr(|T| > |t|)– This is the two-tailed p-value computed using the t distribution. It is the probability of observing a greater absolute value of t under the null hypothesis. If the p-value is less than the pre-specified alpha level (usually .05 or .01, here the former) we will conclude that mean difference between write and read is statistically significantly different from zero. For example, the p-value for the difference between write and read is greater than 0.05 so we conclude that the mean difference is not statistically significantly different from 0.
k. Pr(T < t), Pr(T > t)- These are the one-tailed p-values for evaluating the alternatives (mean < H0 value) and (mean > H0 value), respectively. Like Pr(|T| > |t|), they are computed using the t distribution. Again, if the p-value is less than the pre-specified alpha level (usually .05 or .01) we will conclude that mean difference is statistically significantly greater than or less than zero.
Independent group t-test
This t-test is designed to compare means of same variable between two groups. In our example, we compare the mean writing score between the group of female students and the group of male students. Ideally, these subjects are randomly selected from a larger population of subjects. The test assumes that variances for the two populations are the same. The interpretation for p-value is the same as in other type of t-tests.
In this example, the t-statistic is -3.7341 with 198 degrees of freedom. The corresponding two-tailed p-value is 0.0002, which is less than 0.05. We conclude that the difference of means in write between males and females is different from 0.
ttest write, by(female)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
male | 91 50.12088 1.080274 10.30516 47.97473 52.26703
female | 109 54.99083 .7790686 8.133715 53.44658 56.53507
---------+--------------------------------------------------------------------
combined | 200 52.775 .6702372 9.478586 51.45332 54.09668
---------+--------------------------------------------------------------------
diff | -4.869947 1.304191 -7.441835 -2.298059
------------------------------------------------------------------------------
diff = mean(male) - mean(female) t = -3.7341
Ho: diff = 0 degrees of freedom = 198
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0001 Pr(|T| > |t|) = 0.0002 Pr(T > t) = 0.9999
Summary Statistics
—————————————————————————— Groupa | Obsb Meanc Std. Err.d Std. Dev.e [95% Conf. Interval]f ———+——————————————————————–
male | 91 50.12088 1.080274 10.30516 47.97473 52.26703
female | 109 54.99083 .7790686 8.133715 53.44658 56.53507
---------+--------------------------------------------------------------------
combined | 200 52.775 .6702372 9.478586 51.45332 54.09668
---------+--------------------------------------------------------------------
diff | -4.869947 1.304191 -7.441835 -2.298059
------------------------------------------------------------------------------
a. Group – This column gives categories of the independent variable, in our case female. This variable is specified by the by(female) statement.
b. Obs – This is the number of valid (i.e., non-missing) observations in each group.
c. Mean – This is the mean of the dependent variable for each level of the independent variable. On the last line the difference between the means is given.
d. Std Err – This is the standard error of the mean for each level of the independent variable.
e. Std Dev – This is the standard deviation of the dependent variable for each of the levels of the independent variable. On the last line the standard deviation for the difference is given.
f. [95% Conf. Interval] – These are the lower and upper confidence limits of the means.
Test Statistics
diff = mean(male) – mean(female)g t = -3.7341h Ho: diff = 0 degrees of freedom = 198i
Ha: diff < 0k Ha: diff != 0j Ha: diff > 0k Pr(T < t) = 0.0001 Pr(|T| > |t|) = 0.0002 Pr(T > t) = 0.9999
g. diff = mean(male) – mean(female) – The t-test compares the means between the two groups, the null hypothesis being that the difference between the means is zero.
h. t – This is the t-statistic. It is the ratio of the mean of the difference to the standard error of the difference: (-4.869947/1.304191).
i. degrees of freedom – The degrees of freedom for the paired observations is simply the number of observations minus 2. We use one degree of freedom for estimating the mean of each group, and because there are two groups, we subtract two degrees of freedom.
j. Pr (|T| > |t|) – This is the two-tailed p-value computed using the t distribution. It is the probability of observing a greater absolute value of t under the null hypothesis. If p-value is less than the pre-specified alpha level (usually .05 or .01, here the former) we will conclude that mean is statistically significantly different from zero. For example, the p-value for the difference between females and males is less than 0.05, so we conclude that the difference in means is statistically significantly different from 0.
k. Pr(T < t), Pr(T>t) – These are the one-tailed p-values for the alternative hypotheses (mean difference < 0) and (mean difference > 0), respectively. Like Pr(|T| > |t|), they are computed using the t distribution. As usual, if p-value is less than the pre-specified alpha level (usually .05 or .01) we will conclude that mean is statistically significantly greater or less than zero.
Independent sample T-test assuming unequal variances
We are again going to compare means of the same variable between two groups. In our example, we compare the mean writing score between the group of female students and the group of male students. Ideally, these subjects are randomly selected from a larger population of subjects. We previously assumed that the variances for the two populations are the same. Here, we will allow for unequal variances in our samples. The interpretation for p-value is the same as in other type of t-tests.
In this example, the t-statistic is -3.6564 with 169.707 degrees of freedom. The corresponding two-tailed p-value is 0.0003, which is less than 0.05. We conclude that the difference of means in write between males and females is different from 0, allowing for differences in variances across groups.
ttest write, by(female) unequal
Two-sample t test with unequal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
male | 91 50.12088 1.080274 10.30516 47.97473 52.26703
female | 109 54.99083 .7790686 8.133715 53.44658 56.53507
---------+--------------------------------------------------------------------
combined | 200 52.775 .6702372 9.478586 51.45332 54.09668
---------+--------------------------------------------------------------------
diff | -4.869947 1.331894 -7.499159 -2.240734
------------------------------------------------------------------------------
diff = mean(male) - mean(female) t = -3.6564
Ho: diff = 0 Satterthwaite's degrees of freedom = 169.707
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0002 Pr(|T| > |t|) = 0.0003 Pr(T > t) = 0.9998
Summary Statistics
---------------------------------------------------------------------------------- Groupa | Obsb Meanc Std. Err.d Std. Dev.e [95% Conf. Interval]f ----------+----------------------------------------------------------------------- male | 91 50.12088 1.080274 10.30516 47.97473 52.26703 female | 109 54.99083 .7790686 8.133715 53.44658 56.53507 ----------+----------------------------------------------------------------------- combined | 200 52.775 .6702372 9.478586 51.45332 54.09668 ----------+----------------------------------------------------------------------- diff | -4.869947 1.331894 -7.499159 -2.240734 ----------------------------------------------------------------------------------
a. Group – The list of groups whose means are being compared.
b. Obs. – This is the number of valid observations (ie. non-missing) from each group as well as the combined.
c. Mean – This is the mean of the variable of interest for each group we are comparing. On the third line the combined mean is given and on the last line the difference between the means is given.
d. Std. Err. – This is the standard error of the mean.
e. Std. Dev. – This is the standard deviation of the dependent variable for each of the groups.
f. 95% Confidence interval – These are the lower and upper limits for the 95% confidence interval of the mean for each of the groups.
Test Statistics
diffg = mean(male) - mean(female) th = -3.6564 Ho: diff = 0 Satterthwaite's degrees of freedomi = 169.707 Ha: diff < 0 Ha: diff != 0 Ha: diff > 0 Pr(T < t)k = 0.0002 Pr(|T| > |t|)j = 0.0003 Pr(T > t)k = 0.9998
g. diff – This is the value we are testing: the difference in the means of the male group and the female group.
h. t – This is the t-statistic. It is the test statistic we will use to evaluate our hypothesis. It is the ratio of the mean to the standard error of the difference of the two groups: (-4.869947/1.331894).
i. Satterthwaite’s degrees of freedom – Satterthwaite’s is an alternative way to calculate the degrees of freedom that takes into account that the variances are assumed to be unequal. It is a more conservative approach than using the traditional degrees of freedom. This is the degrees of freedom under this calculation.
j. Pr(|T| > |t|) – This is the two-tailed p-value computed using the t distribution. It is the probability of observing a greater absolute value of t under the null hypothesis. If p-value is less than the pre-specified alpha level (usually .05 or .01, here the former) we will conclude that the difference in means is statistically significantly different from zero. For example, the p-value for the difference between females and males is less than 0.05, so we conclude that the difference in means is statistically significantly different from 0.
l. Pr(T < t), Pr(T > t) – These are the one-tailed p-values for the alternative hypotheses (difference < 0) and (difference > 0), respectively. Like Pr(|T| > |t|), they are computed using the t distribution. As usual, if p-value is less than the pre-specified alpha level (usually .05 or .01) we will conclude that mean is statistically significantly greater or less than zero.
