R2 and adjusted R2 are often used to assess the fit of OLS regression models. Below we show how to estimate the R2 and adjusted R2 using the user-written command mibeta, as well as how to program these calculations yourself in Stata. Note that mibeta uses the mi estimate command, which was introduced in Stata 11. The code to calculate the MI estimates of the R2 and adjusted R2 can be used with earlier versions of Stata, as well as with Stata 11. Additionally, the code to calculate R2 and adjusted R2 “by hand” allows one to calculate confidence intervals (based on Harel 2009), while mibeta does not.
Background
Without going into detail, the MI estimate of a parameter (e.g. a regression coefficient) is the average of the estimated coefficients from the MI datasets. The MI estimate of the standard error of a parameter is calculated based on the standard error of the coefficient in the individual imputations (sometimes called the within imputation variance) and the degree to which the coefficient estimates vary across the imputations (the between imputation variance). For more information on multiple imputation, see the “See also” section at the bottom of the page.
R2 is (among other things) the squared correlation (denoted r) between the observed and expect values of the dependent variable, in equation form: r = sqrt(R2). As mentioned above, the MI estimate of a parameter is typically the mean value across the imputations, and this method can be used to estimate the R2 for an MI model. However, because of the way values of R2 are distributed, directly averaging the values may not be the most appropriate method of calculating the central tendency (i.e. mean) of the distribution. It is possible to transform correlation coefficients so that the mean becomes a more reasonable estimate of central tendency. The mibeta command allows you to use either the values of R2 directly, or a transformation to calculate the MI estimate of R2. The code to estimate the R2 and adjusted R2 “by hand” shows how to calculate these values using a transformation, but can be modified to calculate the values without the transformation.
Harel (2009) suggests using Fisher’s r to z transformation when calculating MI estimates of R2 and adjusted R2. Harel’s method is to first estimate the model and calculate the R2 and/or adjusted R2 in each of the imputed datasets. Each model R2 is then transformed into a correlation (r) by taking its square-root. Fisher’s r to z transformation is then used to transform each of the r values into a z value. The average z across the imputations can then be calculated. Finally, the mean of the z values is transformed back into an R2. The same procedure can be used for adjusted R2 values. A few things should be noted about this procedure. First, Harel writes that the technique works best when the number of imputations is large. Harel also notes that as with any number of statistical procedures, this method works best in large samples. Finally, the results of a simulation study (presented in Harel 2009), suggest that the resulting estimates of R2 tend to be biased upwards (i.e. are too large), while estimates of adjusted R2 tend to be biased downwards (i.e. are too small). Because both estimates tend to be biased, but in opposite directions, calculating the MI estimate for both R2 and adjusted R2 may be useful.
Fisher’s r to z
You may be curious about how the r to z transformation is calculated. Transforming r (i.e. a correlation) to z is a fairly simple process. The value z is the inverse hyperbolic tangent of r, this value can also be written as the following expression:
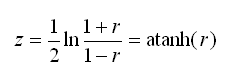
Stata’s atanh(…) function can be used to perform this transformation. The variance of z can also be estimated, this variance is later used in the calculation of a confidence interval for the MI estimate of R2. The formula for the variance of z is simple (note that it depends only on n, i.e. sample size):
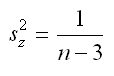
To reverse the r to z transformation, we can find the hyperbolic tangent of z, which can also be written as:
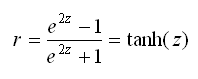
Stata’s tanh(…) function can be used to reverse the transformation.
MI estimates of R2 using mibeta
In order to use the mibeta command, you must first download the necessary files. You can locate mibeta using the command search mibeta . For more information on installing user-written packages in Stata see our FAQ: How do I use the search command to search for programs and additional help? .
Below we open the dataset we will use for this example. You can download the dataset here: mvn_imputation or simply use the command below. The dataset has been mi set so that it will work with Stata’s built in mi commands (introduced in version 11), but we can use mi set (without any arguments) to confirm that the data has been mi set. The output confirms that the data has been mi set and that there are 5 imputations.
use https://stats.idre.ucla.edu/wp-content/uploads/2016/02/mvn_imputation, clear mi set flong, M = 5
For our model, we will predict the variable read, using write and math. Below we use mibeta to estimate the regression model along with the estimates of the R2 and the adjusted R2 using the MI data. Remember that you have to install the mibeta package first! As is typical for regression commands in Stata, the syntax for mibeta is simply the command name followed by the outcome variable (read) and the predictor variables (write and math). Note that we do not specify regress, this is assumed.
mibeta read write math
Multiple-imputation estimates Imputations = 5
Linear regression Number of obs = 200
Average RVI = 0.0827
Complete DF = 197
DF adjustment: Small sample DF: min = 92.88
avg = 134.23
max = 177.77
Model F test: Equal FMI F( 2, 119.8) = 84.86
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
write | .3754693 .0738669 5.08 0.000 .2293537 .5215849
math | .4739484 .0723394 6.55 0.000 .3311939 .616703
_cons | 7.3371 3.597566 2.04 0.044 .1929292 14.48127
------------------------------------------------------------------------------
Standardized coefficients and R-squared
Summary statistics over 5 imputations
| mean min p25 median p75 max
-------------+----------------------------------------------------------------
write | .343877 .328 .3339322 .3446888 .3516272 .361
math | .4310601 .421 .4231636 .4264212 .4272021 .458
-------------+----------------------------------------------------------------
R-square | .4855069 .454 .4837243 .4907281 .4964925 .503
Adj R-square | .4802836 .448 .4784829 .4855579 .4913808 .498
------------------------------------------------------------------------------
The first part of the output produced by mibeta is the imputation information and table of estimates produced by mi estimate. This is the same output that would have been produced if we used the command mi estimate: regress read write math . The second table includes information on standardized coefficients for write and math, as well as the R2 and adjusted R2. The table includes mean, minimum, maximum, and the quartiles of the distribution for each of these values across the imputed datasets. For example, the average R2 (i.e. the MI estimate) is .49, the lowest R2 from the 5 imputed datasets was .45 and the highest was .50.
As discussed above, it may make more sense to transform R2 values before estimating their mean, and then back transform in order to get interpretable values. We can use the mibeta command to estimate the mean of the R2 and adjusted R2 (as well as the standardized coefficients) using Fisher’s r to z transformation with the fisherz option as shown below. Note that only the means will be different from the output above, because the transformation does not change the order of the values.
mibeta read write math, fisherz
Multiple-imputation estimates Imputations = 5
Linear regression Number of obs = 200
Average RVI = 0.0827
Complete DF = 197
DF adjustment: Small sample DF: min = 92.88
avg = 134.23
max = 177.77
Model F test: Equal FMI F( 2, 119.8) = 84.86
Within VCE type: OLS Prob > F = 0.0000
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
write | .3754693 .0738669 5.08 0.000 .2293537 .5215849
math | .4739484 .0723394 6.55 0.000 .3311939 .616703
_cons | 7.3371 3.597566 2.04 0.044 .1929292 14.48127
------------------------------------------------------------------------------
Standardized coefficients and R-squared
Summary statistics over 5 imputations
| mean* min p25 median p75 max
-------------+----------------------------------------------------------------
write | .3439318 .328 .3339322 .3446888 .3516272 .361
math | .4311597 .421 .4231636 .4264212 .4272021 .458
-------------+----------------------------------------------------------------
R-square | .485636 .454 .4837243 .4907281 .4964925 .503
Adj R-square | .4804108 .448 .4784829 .4855579 .4913808 .498
------------------------------------------------------------------------------
* based on Fisher's z transformation
Calculating MI estimates of R2 “by hand”
Below we show how to perform the calculations done by mibeta using Stata syntax. As mentioned above, this method does not require access to the suite of mi commands introduced in Stata 11. This method also has the advantage of allowing for the calculation of confidence intervals.
We will discuss the code to calculate the MI estimate of R2 in pieces, then the entire block of syntax is given at the end of the page so that you can easily transfer it to a .do file and run all of the code at once. Note that because the code uses local macros, all of the code except opening the dataset and using the mi set command must be run at the same time. For clarity the syntax presented step by step shows the process using only R2, however, the code shown at the bottom includes calculations for both the R2 and adjusted R2.
First, let’s open the dataset. The dataset has been mi set to work with Stata’s built in mi commands (introduced in version 11), but we can use mi set (without any arguments) to confirm that the data is formatted the way I think it is. It is important to know how the data is formatted because in order for the syntax below to work properly, the dataset must be stored in what Stata calls the flong style, this is essentially the same format used by mim and produced by ice. The output from mi set confirms that the data is formatted for Stata’s mi commands, is stored in the flong style, and that number of imputations is equal to 5. If the dataset was mi set, but not in the flong style, we could use the command mi convert flong to convert it to the flong style.
use https://stats.idre.ucla.edu/stat/stata/seminars/missing_data/mvn_imputation, clear mi set flong, M = 5
The first line of syntax below creates a local macro that contains the name of the variable that identifies the imputation number. You can think of a local macro as a placeholder for another piece of information, later we will type `mid’ and Stata will interpret this to mean _mi_m . You may need to change the variable name depending on how your dataset is formatted. If the data has been mi set, the variable _mi_m identifies the imputations, if the variable is formatted for mim, or was imputed by ice, the imputation number is probably stored in the variable _mj. The second line creates a scalar, another type of placeholder, that contains the number of imputations, in this case, 5. The next line uses generate to create a new variable, r2, this will be used to store the R2 from each of the MI datasets. You can modify this line by changing the variable name or by removing it entirely (in which case the values from individual MI datasets won’t be stored, but everything else will work the same way). If you chose to do either, you must also modify the some of the syntax below to reflect these changes (this will be noted as we go along). The final two lines create an M by 1 vector (mz) that will be used to store the transformed values of R2 so that we can make use of them.
local mid = "_mi_m" scalar M = 5 gen r2 = . matrix mz = J(M,1,0)
The block of syntax below runs the regression model once in each of the imputations, and saves the information necessary to calculate the MI estimate of the R2. In the first line of syntax, the forvalues command tells Stata that the commands between the curved brackets (i.e. { and } ) should be repeated once for the values one to M (i.e. 1/`=M’). Because we defined M as a scalar above (equal to 5), Stata will interpret `=M’ as being 5, so the loop will repeat for the values 1 to 5. Note that the two symbols that surround M are different, the first (i.e. ` ) is on the same key as the tilde (i.e. ~), and the character following M (i.e. ‘ ) is an apostrophe, sometimes called a single quote. Each time the commands within the loop are repeated, the local macro m takes on a new value (by default, whole number values are used, i.e. 1, 2,…,5).
Looking at the syntax within the brackets, the first line contains the model we wish to estimate. The quietly: prefix tells Stata to estimate the model, without displaying the output. The command name, regress, is followed by the name of the outcome variable, and then the list of predictor variables. The if(…) tells Stata to estimate the model for one imputation at a time, using the local macro mid we defined above (i.e. the name of variable that indexes the imputations), as well as the local macro m. You can change the model to reflect your analysis, and you can omit the quietly: prefix, but the if(…) must remain (although you could add to it if necessary). When Stata estimates the regression model, it temporarily stores information from the model, including the model R2 which is stored as e(r2). The next line performs the r to z transformation on e(r2) (i.e. atanh(sqrt(e(r2))) ), and saves the value in the appropriate row of the matrix mz. The final line saves the value of the R2 from the model in the variable r2. If you are not creating this variable, you should delete this command.
forvalues m = 1/`=M' {
quietly: regress read write math if(`mid'==`m')
matrix mz[`m',1] = atanh(sqrt(e(r2)))
replace r2 = e(r2) in `m'
}
Now the matrix mz contains the z values (i.e. the transformed R2 values) from each of the imputed datasets. We will use Stata’s matrix language, Mata, to perform some of the calculations necessary to generate the MI estimates of R2 and its confidence interval. The first step is to pass the scalar containing the number of imputations (i.e. M), and the matrix containing the R2 values (i.e. mz) to Mata. The st_numscalar(…), and st_matrix(…) commands allow us to pass information from Stata to Mata, and vice versa.
mata: M = st_numscalar("M")
mata: z = st_matrix("mz")
Above we used st_numscalar(…) to pass information from Stata to Mata, in the syntax below we use it to pass information from Mata to Stata. Below we place the mean of z (i.e. the mean of the z values) in the scalar value Q. Q now holds the MI estimate of z, which we will later transform back into to the MI estimate of R2.
mata: st_numscalar("Q", mean(z))
To compute the variance of pooled R2 we use Rubin’s formula (Rubin, 1987) which partitions total variance into “within imputation” capturing the expected uncertainty, “between imputation” capturing the estimation variability due to missing information, and an additional sampling variance. The total variance is: VT = Vw + VB (1 + 1/m )
In the first line below we use Mata to estimate the between imputation variance based on the standard formulas for MI, this value is denoted b. The between imputation variance is used in the calculation of the confidence intervals. The second line below uses st_numscalar to pass b from Mata to Stata, note that in Stata we have named the scalar B, rather than b.
mata: b = sum((z :- mean(z)):^2)/(M-1)
mata: st_numscalar("B" , b )
As mentioned above the variance of z is based only on n, this results in a within imputation variance that is constant (1/(n-3)). The within and between variances are combined to form V, the MI estimate of the variance of z. The first line below uses the sample size (stored e(N)), the between imputation variance (stored in B), and the number of imputations (stored in M) to calculate the total variance of z. The following two lines, use the MI estimate of z (i.e. Q), along with the estimate of V, to calculate the upper and lower 95% confidence limits for z.
scalar def V = 1/(e(N)-3) + B + B/M scalar def uci = Q + 1.959964*sqrt(V) scalar def lci = Q - 1.959964*sqrt(V)
The first line of syntax below begins with the display command, followed by some text to display, and the expression ((tanh(r2z/`M’))^2). This expression reverses the r to z transformation, and squares r to give the estimated R2. The second line does the same for the upper and lower confidence limits.
di "Average R-squared = " (tanh(Q))^2 Average R-squared = .48563602 di "95% CI [" tanh(lci)^2 "," tanh(uci)^2 "]" _n 95% CI [.38278305,.57971497]
If you stored the values of the R2 from each imputation as variables in the dataset, you can sort by the variable r2, and then list the non-missing values of r2 and r2_a. This allows you to see the range of values for R2 and adjusted R2 across the imputations.
sort r2
list r2 if r2!=.
+----------+
| r2 |
|----------|
1. | .4536123 |
2. | .4837243 |
3. | .4907281 |
4. | .4964925 |
5. | .5029773 |
+----------+
Below is syntax to compute the MI estimate and its confidence interval in a single block. Note that unlike the above example, this syntax estimates both the R2 and the adjusted R2. As discussed above, it may be useful to calculate MI estimates for both the R2 and adjusted R2 because R2 tends to be biased upwards while the adjusted R2 tends to be biased downward. The estimate of the adjusted R2 for each regression model is stored by Stata as e(r2_a) and all subsequent values related to the adjusted R2 have the same name as for the R2 with the suffix _a (e.g. the variables r2 and r2_a).
use https://stats.idre.ucla.edu/stat/stata/seminars/missing_data/mvn_imputation, clear
mi set
* EDIT: Depending on the dataset format, _mi_m may need to be replaced with _mj (ice/mim)
* or some other variable name. M should be set to equal to the number of imputations.
local mid = "_mi_m"
scalar M = 5
* generate variables to save the R^2 and adjusted R^2 from each imputation in a variable
* this is optional, but if you remove this or change the variable names,
* you will also need to edit more below.
gen r2 = .
gen r2_a = .
* create vectors
matrix mz = J(M,1,0)
matrix mz_a = J(M,1,0)
forvalues m = 1/`=M' {
* EDIT: Define your model here, the command must include the if
quietly: reg read write math if(`mid'==`m')
* write resulting z values to the matrix
matrix mz[`m',1] = atanh(sqrt(e(r2)))
matrix mz_a[`m',1] = atanh(sqrt(e(r2_a)))
* save the value of R^2 and the adjusted R^2 (optional, may require editing)
replace r2 = e(r2) in `m'
replace r2_a = e(r2_a) in `m'
}
* Pass information to Mata
mata: M = st_numscalar("M")
mata: z = st_matrix("mz")
mata: z_a = st_matrix("mz_a")
* MI estimate of z (i.e. mean of z)
mata: st_numscalar("Q", mean(z))
mata: st_numscalar("Q_a", mean(z_a))
* Calculate the between variance
* R^2
mata: B = sum((z :- mean(z)):^2)/(M-1)
mata: st_numscalar("B" , B )
* Adjusted R^2
mata: B_a = sum((z_a :- mean(z_a)):^2)/(M-1)
mata: st_numscalar("B_a" , B_a )
* Total variance (V). Note the within variance only needs to be calculated once
* because the n should be constant (w = 1/(n-3))
scalar def V = 1/(e(N)-3) + B + B/M
scalar def V_a = 1/(e(N)-3) + B_a + B_a/M
* CIs for z scale
* CI Q +/- z*sqrt(V)
scalar def uci = Q + 1.959964*sqrt(V)
scalar def lci = Q - 1.959964*sqrt(V)
scalar def uci_a = Q_a + 1.959964*sqrt(V_a)
scalar def lci_a = Q_a - 1.959964*sqrt(V_a)
* display results
di "Average R-squared = " (tanh(Q))^2
di "95% CI [" tanh(lci)^2 "," tanh(uci)^2 "]" _n
di "Average Adjusted R-squared = " (tanh(Q_a))^2
di "95% CI [" tanh(lci_a)^2 "," tanh(uci_a)^2 "]"
* if you have created variables with R^2 from each imputation (optional)
sort r2
list r2 r2_a if r2!=.
See also
- Missing Data: A Gentle Introduction by McKnight, McKnight, Sidani, and Figueredo (2007).
- Statistical Analysis with Missing Data, Second Edition by Little and Rubin (2002).
- Multiple Imputation in Stata Seminar
Citations
Harel, O. (2009). The estimation of R2 and adjusted R2 in incomplete data sets using multiple imputation. Journal of Applied Statistics, 36(10), 1109-1118.
