Version info: Code for this page was tested in Stata 12.
Truncated regression is used to model dependent variables for which some of the observations are not included in the analysis because of the value of the dependent variable.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of truncated regression
Example 1.
A study of students in a special GATE (gifted and talented education) program wishes to model achievement as a function of language skills and the type of program in which the student is currently enrolled. A major concern is that students are required to have a minimum achievement score of 40 to enter the special program. Thus, the sample is truncated at an achievement score of 40.
Example 2. A researcher has data for a sample of Americans whose income is above the poverty line. Hence, the lower part of the distribution of income is truncated. If the researcher had a sample of Americans whose income was at or below the poverty line, then the upper part of the income distribution would be truncated. In other words, truncation is a result of sampling only part of the distribution of the outcome variable.
Description of the data
Let’s pursue Example 1 from above.
We have a hypothetical data file, truncreg.dta, with 178 observations. The outcome variable is called achiv, and the language test score variable is called langscore. The variable prog is a categorical predictor variable with three levels indicating the type of program in which the students were enrolled.
Let’s look at the data. It is always a good idea to start with descriptive statistics.
use https://stats.idre.ucla.edu/stat/stata/dae/truncreg, clear
summarize achiv langscore
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
achiv | 178 54.23596 8.96323 41 76
langscore | 178 54.01124 8.944896 31 67
tabstat achiv, by(prog) stats(n mean sd)
Summary for variables: achiv
by categories of: prog (type of program)
prog | N mean sd
---------+------------------------------
general | 40 51.575 7.97074
academic | 101 56.89109 9.018759
vocation | 37 49.86486 7.276912
---------+------------------------------
Total | 178 54.23596 8.96323
----------------------------------------
histogram achiv, bin(6) start(40) freq normaltabulate prog type of | program | Freq. Percent Cum. ------------+----------------------------------- general | 40 22.47 22.47 academic | 101 56.74 79.21 vocation | 37 20.79 100.00 ------------+----------------------------------- Total | 178 100.00
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- OLS regression – You could analyze these data using OLS regression. OLS regression will not adjust the estimates of the coefficients to take into account the effect of truncating the sample at 40, and the coefficients may be severely biased. This can be conceptualized as a model specification error (Heckman, 1979).
- Truncated regression – Truncated regression addresses the bias introduced when using OLS regression with truncated data. Note that with truncated regression, the variance of the outcome variable is reduced compared to the distribution that is not truncated. Also, if the lower part of the distribution is truncated, then the mean of the truncated variable will be greater than the mean from the untruncated variable; if the truncation is from above, the mean of the truncated variable will be less than the untruncated variable.
- These types of models can also be conceptualized as Heckman selection models, which are used to correct for sampling selection bias.
- Censored regression – Sometimes the concepts of truncation and censoring are confused. With censored data we have all of the observations, but we don’t know the “true” values of some of them. With truncation, some of the observations are not included in the analysis because of the value of the outcome variable. It would be inappropriate to analyze the data in our example using a censored regression model.
Truncated regression
Below we use the truncreg command to estimate a truncated regression model. The i. before prog indicates that it is a factor variable (i.e., categorical variable), and that it should be included in the model as a series of indicator variables. The ll() option in the truncreg command indicates the value at which the left truncation take place. There is also a ul() option to indicate the value of the right truncation, which was not needed in this example.
truncreg achiv langscore i.prog, ll(40)
(note: 0 obs. truncated)
Fitting full model:
Iteration 0: log likelihood = -598.11669
Iteration 1: log likelihood = -591.68374
Iteration 2: log likelihood = -591.31208
Iteration 3: log likelihood = -591.30981
Iteration 4: log likelihood = -591.30981
Truncated regression
Limit: lower = 40 Number of obs = 178
upper = +inf Wald chi2(3) = 54.76
Log likelihood = -591.30981 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
achiv | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
langscore | .7125775 .1144719 6.22 0.000 .4882168 .9369383
|
prog |
2 | 4.065219 2.054938 1.98 0.048 .0376131 8.092824
3 | -1.135863 2.669961 -0.43 0.671 -6.368891 4.097165
|
_cons | 11.30152 6.772731 1.67 0.095 -1.97279 24.57583
-------------+----------------------------------------------------------------
/sigma | 8.755315 .666803 13.13 0.000 7.448405 10.06222
------------------------------------------------------------------------------
In the table of coefficients, we have the truncated regression coefficients, the standard error of the coefficients, the Wald z-tests (coefficient/se), and the p-value associated with each z-test. By default, we also get a 95% confidence interval for the coefficients. With the level() option you can request a different confidence interval.
test 2.prog 3.prog
( 1) [eq1]2.prog = 0
( 2) [eq1]3.prog = 0
chi2( 2) = 7.19
Prob > chi2 = 0.0274
The two degree-of-freedom chi-square test indicates that prog is a statistically significant predictor of achiv.
We can use the margins command to obtain the expected cell means. Note that these are different from the means we obtained with the tabstat command above.
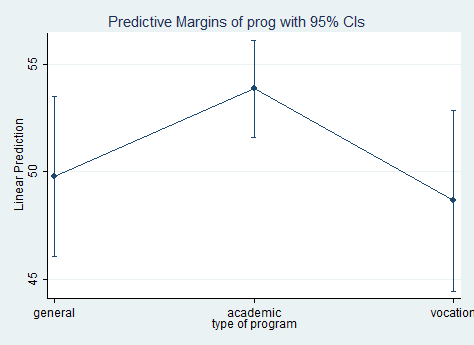
margins prog
Predictive margins Number of obs = 178
Model VCE : OIM
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
1 | 49.78871 1.897166 26.24 0.000 46.07034 53.50709
2 | 53.85393 1.150041 46.83 0.000 51.59989 56.10797
3 | 48.65285 2.140489 22.73 0.000 44.45757 52.84813
------------------------------------------------------------------------------
In the table above, we can see that the expected mean of avchiv for the first level of prog is approximately 49.79; the expected mean for level 2 of prog is 53.85; the expected mean for the third level of prog is 48.65.
marginsplot
If you would like to compare truncated regression models, you can issue the estat ic command to get the log likelihood, AIC and BIC values.
estat ic ----------------------------------------------------------------------------- Model | Obs ll(null) ll(model) df AIC BIC -------------+--------------------------------------------------------------- . | 178 . -591.3098 5 1192.62 1208.529 ----------------------------------------------------------------------------- Note: N=Obs used in calculating BIC; see [R] BIC note
The truncreg output includes neither an R2 nor a pseudo-R2. You can compute a rough estimate of the degree of association by correlating achiv with the predicted value and squaring the result.
predict p correlate p achiv (obs=178) | p achiv -------------+------------------ p | 1.0000 achiv | 0.5524 1.0000 display r(rho)^2 .30519203
The calculated value of .31 is rough estimate of the R2 you would find in an OLS regression. The squared correlation between the observed and predicted academic aptitude values is about 0.31, indicating that these predictors accounted for over 30% of the variability in the outcome variable.
Things to consider
- Stata's truncreg command is designed to work when the truncation is on the outcome variable in the model. It is possible to have samples that are truncated based on one or more predictors. For example, modeling college GPA as a function of high school GPA (HSGPA) and SAT scores involves a sample that is truncated based on the predictors, i.e., only students with higher HSGPA and SAT scores are admitted into the college.
- You need to be careful about what value is used as the truncation value, because it affects the estimation of the coefficients and standard errors. In the example above, if we had used ll(39) instead of ll(40), the results would have been slightly different. It does not matter that there were no values of 40 in our sample.
See also
References
- Greene, W. H. (2003). Econometric Analysis, Fifth Edition. Upper Saddle River, NJ: Prentice Hall.
- Heckman, J. J. (1979). Sample selection bias as a specification error. Econometrica, Volume 47, Number 1, pages 153 - 161.
- Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables.
Thousand Oaks, CA: Sage Publications.