Version info: Code for this page was tested in Stata 12.
Poisson regression is used to model count variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of Poisson regression
Example 1. The number of persons killed by mule or horse kicks in the Prussian army per year. Ladislaus Bortkiewicz collected data from 20 volumes of Preussischen Statistik. These data were collected on 10 corps of the Prussian army in the late 1800s over the course of 20 years.
Example 2. The number of people in line in front of you at the grocery store. Predictors may include the number of items currently offered at a special discounted price and whether a special event (e.g., a holiday, a big sporting event) is three or fewer days away.
Example 3. The number of awards earned by students at one high school. Predictors of the number of awards earned include the type of program in which the student was enrolled (e.g., vocational, general or academic) and the score on their final exam in math.
Description of the data
For the purpose of illustration, we have simulated a data set for Example 3 above. In this example, num_awards is the outcome variable and indicates the number of awards earned by students at a high school in a year, math is a continuous predictor variable and represents students’ scores on their math final exam, and prog is a categorical predictor variable with three levels indicating the type of program in which the students were enrolled.
Let’s start with loading the data and looking at some descriptive statistics.
use https://stats.idre.ucla.edu/stat/stata/dae/poisson_sim, clear
sum num_awards math
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
num_awards | 200 .63 1.052921 0 6
math | 200 52.645 9.368448 33 75
Each variable has 200 valid observations and their distributions seem quite reasonable. In this particular the unconditional mean and variance of our outcome variable are not extremely different.
Let’s continue with our description of the variables in this dataset. The table below shows the average numbers of awards by program type and seems to suggest that program type is a good candidate for predicting the number of awards, our outcome variable, because the mean value of the outcome appears to vary by prog.
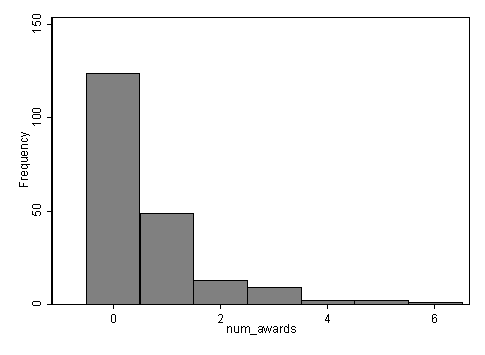
tabstat num_awards, by(prog) stats(mean sd n) Summary for variables: num_awards by categories of: prog (type of program) prog | mean sd N ---------+------------------------------ general | .2 .4045199 45 academic | 1 1.278521 105 vocation | .24 .5174506 50 ---------+------------------------------ Total | .63 1.052921 200 ----------------------------------------histogram num_awards, discrete freq scheme(s1mono) (start=0, width=1)
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Poisson regression – Poisson regression is often used for modeling count data. Poisson regression has a number of extensions useful for count models.
- Negative binomial regression – Negative binomial regression can be used for over-dispersed count data, that is when the conditional variance exceeds the conditional mean. It can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression and it has an extra parameter to model the over-dispersion. If the conditional distribution of the outcome variable is over-dispersed, the confidence intervals for Negative binomial regression are likely to be narrower as compared to those from a Poisson regression.
- Zero-inflated regression model – Zero-inflated models attempt to account for excess zeros. In other words, two kinds of zeros are thought to exist in the data, "true zeros" and "excess zeros". Zero-inflated models estimate two equations simultaneously, one for the count model and one for the excess zeros.
- OLS regression – Count outcome variables are sometimes log-transformed and analyzed using OLS regression. Many issues arise with this approach, including loss of data due to undefined values generated by taking the log of zero (which is undefined) and biased estimates.
Poisson regression
Below we use the poisson command to estimate a Poisson regression model. The i. before prog indicates that it is a factor variable (i.e., categorical variable), and that it should be included in the model as a series of indicator variables.
We use the vce(robust) option to obtain robust standard errors for the parameter estimates as recommended by Cameron and Trivedi (2009) to control for mild violation of underlying assumptions.
poisson num_awards i.prog math, vce(robust)
Iteration 0: log pseudolikelihood = -182.75759
Iteration 1: log pseudolikelihood = -182.75225
Iteration 2: log pseudolikelihood = -182.75225
Poisson regression Number of obs = 200
Wald chi2(3) = 80.15
Prob > chi2 = 0.0000
Log pseudolikelihood = -182.75225 Pseudo R2 = 0.2118
------------------------------------------------------------------------------
| Robust
num_awards | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
2 | 1.083859 .3218538 3.37 0.001 .4530373 1.714681
3 | .3698092 .4014221 0.92 0.357 -.4169637 1.156582
|
math | .0701524 .0104614 6.71 0.000 .0496485 .0906563
_cons | -5.247124 .6476195 -8.10 0.000 -6.516435 -3.977814
------------------------------------------------------------------------------
The two degree-of-freedom chi-square test indicates that prog, taken together, is a statistically significant predictor of num_awards.
test 2.prog 3.prog
( 1) [num_awards]2.prog = 0
( 2) [num_awards]3.prog = 0
chi2( 2) = 14.76
Prob > chi2 = 0.0006
To help assess the fit of the model, the estat gof command can be used to obtain the goodness-of-fit chi-squared test. This is not a test of the model coefficients (which we saw in the header information), but a test of the model form: Does the poisson model form fit our data?
estat gof
Goodness-of-fit chi2 = 189.4496
Prob > chi2(196) = 0.6182
Pearson goodness-of-fit = 212.1437
Prob > chi2(196) = 0.2040
We conclude that the model fits reasonably well because the goodness-of-fit chi-squared test is not statistically significant. If the test had been statistically significant, it would indicate that the data do not fit the model well. In that situation, we may try to determine if there are omitted predictor variables, if our linearity assumption holds and/or if there is an issue of over-dispersion.
Sometimes, we might want to present the regression results as incident rate ratios, we can use the irr option. These IRR values are equal to our coefficients from the output above exponentiated.
poisson, irr
Poisson regression Number of obs = 200
Wald chi2(3) = 80.15
Prob > chi2 = 0.0000
Log pseudolikelihood = -182.75225 Pseudo R2 = 0.2118
------------------------------------------------------------------------------
| Robust
num_awards | IRR Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
2 | 2.956065 .9514208 3.37 0.001 1.573083 5.554903
3 | 1.447458 .5810418 0.92 0.357 .6590449 3.179049
|
math | 1.072672 .0112216 6.71 0.000 1.050902 1.094893
------------------------------------------------------------------------------
The output above indicates that the incident rate for 2.prog is 2.96 times the incident rate for the reference group (1.prog). Likewise, the incident rate for 3.prog is 1.45 times the incident rate for the reference group holding the other variables constant. The percent change in the incident rate of num_awards is an increase of 7% for every unit increase in math.
Recall the form of our model equation:
log(num_awards) = Intercept + b1(prog=2) + b2(prog=3) + b3math.
This implies:
num_awards = exp(Intercept + b1(prog=2) + b2(prog=3)+ b3math) = exp(Intercept) * exp(b1(prog=2)) * exp(b2(prog=3)) * exp(b3math)
The coefficients have an additive effect in the log(y) scale and the IRR have a multiplicative effect in the y scale.
For additional information on the various metrics in which the results can be presented, and the interpretation of such, please see Regression Models for Categorical Dependent Variables Using Stata, Second Edition by J. Scott Long and Jeremy Freese (2006).
To understand the model better, we can use the margins command. Below we use the margins command to calculate the predicted counts at each level of prog, holding all other variables (in this example, math) in the model at their mean values.
margins prog, atmeans
Adjusted predictions Number of obs = 200
Model VCE : Robust
Expression : Predicted number of events, predict()
at : 1.prog = .225 (mean)
2.prog = .525 (mean)
3.prog = .25 (mean)
math = 52.645 (mean)
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
prog |
1 | .211411 .0627844 3.37 0.001 .0883558 .3344661
2 | .6249446 .0887008 7.05 0.000 .4510943 .7987949
3 | .3060086 .0828648 3.69 0.000 .1435966 .4684205
------------------------------------------------------------------------------
In the output above, we see that the predicted number of events for level 1 of prog is about .21, holding math at its mean. The predicted number of events for level 2 of prog is higher at .62, and the predicted number of events for level 3 of prog is about .31. Note that the predicted count of level 2 of prog is (.6249446/.211411) = 2.96 times higher than the predicted count for level 1 of prog. This matches what we saw in the IRR output table.
Below we will obtain the predicted counts for values of math that range from 35 to 75 in increments of 10.
margins, at(math=(35(10)75)) vsquish
Predictive margins Number of obs = 200
Model VCE : Robust
Expression : Predicted number of events, predict()
1._at : math = 35
2._at : math = 45
3._at : math = 55
4._at : math = 65
5._at : math = 75
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | .1311326 .0358696 3.66 0.000 .0608295 .2014358
2 | .2644714 .047518 5.57 0.000 .1713379 .3576049
3 | .5333923 .0575203 9.27 0.000 .4206546 .64613
4 | 1.075758 .1220143 8.82 0.000 .8366147 1.314902
5 | 2.169615 .4115856 5.27 0.000 1.362922 2.976308
------------------------------------------------------------------------------
The table above shows that with prog at its observed values and math held at 35 for all observations, the average predicted count (or average number of awards) is about .13; when math = 75, the average predicted count is about 2.17. If we compare the predicted counts at math = 35 and math = 45, we can see that the ratio is (.2644714/.1311326) = 2.017. This matches the IRR of 1.0727 for a 10 unit change: 1.0727^10 = 2.017.
The user-written fitstat command (as well as Stata’s estat commands) can be used to obtain additional information that may be helpful if you want to compare models. You can type search fitstat to download this program (see How can I used the search command to search for programs and get additional help? for more information about using search).
fitstat
Measures of Fit for poisson of num_awards
Log-Lik Intercept Only: -231.864 Log-Lik Full Model: -182.752
D(195): 365.505 LR(3): 98.223
Prob > LR: 0.000
McFadden's R2: 0.212 McFadden's Adj R2: 0.190
ML (Cox-Snell) R2: 0.388 Cragg-Uhler(Nagelkerke) R2: 0.430
AIC: 1.878 AIC*n: 375.505
BIC: -667.667 BIC': -82.328
BIC used by Stata: 386.698 AIC used by Stata: 373.505
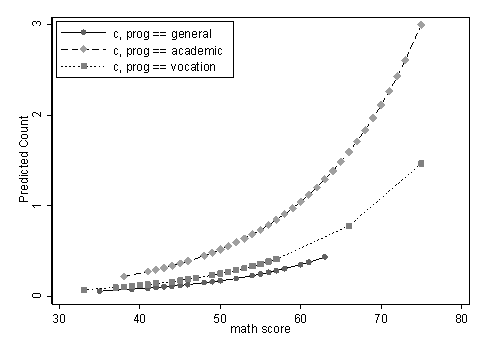
You can graph the predicted number of events with the commands below. The graph indicates that the most awards are predicted for those in the academic program (prog = 2), especially if the student has a high math score. The lowest number of predicted awards is for those students in the general program (prog = 1).
predict c separate c, by(prog) twoway scatter c1 c2 c3 math, connect(l l l) sort /// ytitle("Predicted Count") ylabel( ,nogrid) legend(rows(3)) /// legend(ring(0) position(10)) scheme(s1mono)
Things to consider
- If overdispersion seems to be an issue, we should first check if our model is appropriately specified, such as omitted variables and functional forms. For example, if we omitted the predictor variable prog in the example above, our model would seem to have a problem with over-dispersion. In other words, a mis-specified model could present a symptom like an over-dispersion problem.
- Assuming that the model is correctly specified, you may want to check for overdispersion. There are several ways to do this including the likelihood ratio test of over-dispersion parameter alpha by running the same regression model using negative binomial distribution (nbreg).
- One common cause of over-dispersion is excess zeros, which in turn are generated by an additional data generating process. In this situation, zero-inflated model should be considered.
- If the data generating process does not allow for any 0s (such as the number of days spent in the hospital), then a zero-truncated model may be more appropriate.
- Count data often have an exposure variable, which indicates the number of times the event could have happened. This variable should be incorporated into a Poisson model with the use of the exp() option.
- The outcome variable in a Poisson regression cannot have negative numbers, and the exposure cannot have 0s.
- In Stata, a Poisson model can be estimated via glm command with the log link and the Poisson family.
- You will need to use the glm command to obtain the residuals to check other assumptions of the Poisson model (see Cameron and Trivedi (1998) and Dupont (2002) for more information).
- Many different measures of pseudo-R-squared exist. They all attempt to provide information similar to that provided by R-squared in OLS regression, even though none of them can be interpreted exactly as R-squared in OLS regression is interpreted. For a discussion of various pseudo-R-squares, see Long and Freese (2006) or our FAQ page What are pseudo R-squareds?.
- Poisson regression is estimated via maximum likelihood estimation. It usually requires a large sample size.
See also
- Annotated output for the poisson command
- Stata FAQ: How can I use countfit in choosing a count model?
- Stata online manual
- Stata FAQs
References
- Cameron, A. C. and Trivedi, P. K. (2009). Microeconometrics Using Stata. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. (1998). Regression Analysis of Count Data. New York: Cambridge Press.
- Cameron, A. C. Advances in Count Data Regression Talk for the Applied Statistics Workshop, March 28, 2009. http://cameron.econ.ucdavis.edu/racd/count.html .
- Dupont, W. D. (2002). Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data. New York: Cambridge Press.
- Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
- Long, J. S. and Freese, J. (2006). Regression Models for Categorical Dependent Variables Using Stata, Second Edition. College Station, TX: Stata Press.