Version info: Code for this page was tested in Stata 12.
Negative binomial regression is for modeling count variables, usually for over-dispersed count outcome variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of negative binomial regression
Example 1. School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include the type of program in which the student is enrolled and a standardized test in math.
Example 2. A health-related researcher is studying the number of hospital visits in past 12 months by senior citizens in a community based on the characteristics of the individuals and the types of health plans under which each one is covered.
Description of the data
Let’s pursue Example 1 from above.
We have attendance data on 314 high school juniors from two urban high schools in the file nb_data.dta. The response variable of interest is days absent, daysabs. The variable math is the standardized math score for each student. The variable prog is a three-level nominal variable indicating the type of instructional program in which the student is enrolled.
Let’s look at the data. It is always a good idea to start with descriptive statistics and plots.
use https://stats.idre.ucla.edu/stat/stata/dae/nb_data, clear summarize daysabs mathVariable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- daysabs | 314 5.955414 7.036958 0 35 math | 314 48.26752 25.36239 1 99 histogram daysabs, discrete freq scheme(s1mono)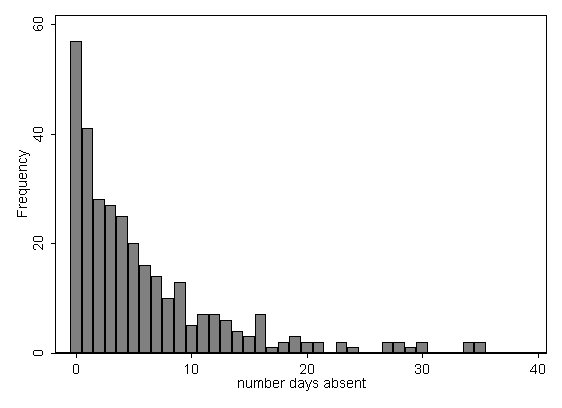
Each variable has 314 valid observations and their distributions seem quite reasonable. The unconditional mean of our outcome variable is much lower than its variance.
Let’s continue with our description of the variables in this dataset. The table below shows the average numbers of days absent by program type and seems to suggest that program type is a good candidate for predicting the number of days absent, our outcome variable, because the mean value of the outcome appears to vary by prog. The variances within each level of prog are higher than the means within each level. These are the conditional means and variances. These differences suggest that over-dispersion is present and that a Negative Binomial model would be appropriate.
tabstat daysabs, by(prog) stats(mean v n)
Summary for variables: daysabs
by categories of: prog
prog | mean variance N
---------+------------------------------
1 | 10.65 67.25897 40
2 | 6.934132 55.44744 167
3 | 2.672897 13.93916 107
---------+------------------------------
Total | 5.955414 49.51877 314
----------------------------------------
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Negative binomial regression – Negative binomial regression can be used for over-dispersed count data, that is when the conditional variance exceeds the conditional mean. It can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression and it has an extra parameter to model the over-dispersion. If the conditional distribution of the outcome variable is over-dispersed, the confidence intervals for the Negative binomial regression are likely to be narrower as compared to those from a Poisson regression model.
- Poisson regression – Poisson regression is often used for modeling count data. Poisson regression has a number of extensions useful for count models.
- Zero-inflated regression model – Zero-inflated models attempt to account for excess zeros. In other words, two kinds of zeros are thought to exist in the data, “true zeros” and “excess zeros”. Zero-inflated models estimate two equations simultaneously, one for the count model and one for the excess zeros.
- OLS regression – Count outcome variables are sometimes log-transformed and analyzed using OLS regression. Many issues arise with this approach, including loss of data due to undefined values generated by taking the log of zero (which is undefined), as well as the lack of capacity to model the dispersion.
Negative binomial regression analysis
Below we use the nbreg command to estimate a negative binomial regression model. The i. before prog indicates that it is a factor variable (i.e., categorical variable), and that it should be included in the model as a series of indicator variables.
nbreg daysabs math i.prog Fitting Poisson model: Iteration 0: log likelihood = -1328.6751 Iteration 1: log likelihood = -1328.6425 Iteration 2: log likelihood = -1328.6425 Fitting constant-only model: Iteration 0: log likelihood = -899.27009 Iteration 1: log likelihood = -896.47264 Iteration 2: log likelihood = -896.47237 Iteration 3: log likelihood = -896.47237 Fitting full model: Iteration 0: log likelihood = -870.49809 Iteration 1: log likelihood = -865.90381 Iteration 2: log likelihood = -865.62942 Iteration 3: log likelihood = -865.6289 Iteration 4: log likelihood = -865.6289 Negative binomial regression Number of obs = 314 LR chi2(3) = 61.69 Dispersion = mean Prob > chi2 = 0.0000 Log likelihood = -865.6289 Pseudo R2 = 0.0344 ------------------------------------------------------------------------------ daysabs | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | -.005993 .0025072 -2.39 0.017 -.010907 -.001079 | prog | 2 | -.44076 .182576 -2.41 0.016 -.7986025 -.0829175 3 | -1.278651 .2019811 -6.33 0.000 -1.674526 -.882775 | _cons | 2.615265 .1963519 13.32 0.000 2.230423 3.000108 -------------+---------------------------------------------------------------- /lnalpha | -.0321895 .1027882 -.2336506 .1692717 -------------+---------------------------------------------------------------- alpha | .9683231 .0995322 .7916384 1.184442 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 926.03 Prob>=chibar2 = 0.000
- The output begins the iteration log. We can see that it starts with fitting a Poisson model, then a null model (intercept only model) and finally the negative binomial model. Since it uses maximum likelihood estimate, it iterates until the change in the log likelihood is sufficiently small. The last value in the iteration log is the final value of the log likelihood for the full model and is displayed again. The log likelihood can be used to compare models.
- The header information is presented next. On the right-hand side, the number of observations used in the analysis (314) is given, along with the Wald chi-square statistic with three degrees of freedom for the full model, followed by the p-value for the chi-square. This is a test that all of the estimated coefficients are equal to zero–a test of the model as a whole. From the p-value, we can see that the model is statistically significant. The header also includes a pseudo-R2, which is 0.03 in this example.
- Below the header you will find the negative binomial regression coefficients for each of the variables, along with standard errors, z-scores, p-values and 95% confidence intervals for the coefficients. The variable math has a coefficient of -0.006, which is statistically significant. This means that for each one-unit increase on math, the expected log count of the number of days absent decreases by 0.006. The indicator variable 2.prog is the expected difference in log count between group 2 (prog=2) and the reference group (prog=1). The expected log count for level 2 of prog is 0.44 lower than the expected log count for level 1. The indicator variable 3.prog is the expected difference in log count between group 3 (prog=3) and the reference group (prog=1). The expected log count for level 3 of prog is 1.28 lower than the expected log count for level 1. To determine if prog itself, overall, is statistically significant, we can use the test command to obtain the two degrees-of-freedom test of this variable. The two degree-of-freedom chi-square test indicates that prog is a statistically significant predictor of daysabs.
test 2.prog 3.prog ( 1) [daysabs]2.prog = 0 ( 2) [daysabs]3.prog = 0 chi2( 2) = 49.21 Prob > chi2 = 0.0000
- Additionally, the log-transformed over-dispersion parameter (/lnalpha) is estimated and is displayed along with the untransformed value. A Poisson model is one in which this alpha value is constrained to zero. Stata finds the maximum likelihood estimate of the log of alpha and then calculates alpha from this. This means that alpha is always greater than zero and that Stata’s nbreg only allows for overdispersion (variance greater than the mean).
- Below the table of coefficients, you will find a likelihood ratio test that alpha equals zero–the likelihood ratio test comparing this model to a Poisson model. In this example the associated chi-squared value is 926.03 with one degree of freedom. This strongly suggests that alpha is non-zero and the negative binomial model is more appropriate than the Poisson model.
We can also see the results as incident rate ratios by using the irr option.
nbreg, irrNegative binomial regression Number of obs = 314 LR chi2(3) = 61.69 Dispersion = mean Prob > chi2 = 0.0000 Log likelihood = -865.6289 Pseudo R2 = 0.0344 ------------------------------------------------------------------------------ daysabs | IRR Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | .9940249 .0024922 -2.39 0.017 .9891523 .9989216 | prog | 2 | .6435471 .1174963 -2.41 0.016 .4499573 .920427 3 | .2784127 .0562341 -6.33 0.000 .1873969 .4136335 -------------+---------------------------------------------------------------- /lnalpha | -.0321895 .1027882 -.2336506 .1692717 -------------+---------------------------------------------------------------- alpha | .9683231 .0995322 .7916384 1.184442 ------------------------------------------------------------------------------ Likelihood-ratio test of alpha=0: chibar2(01) = 926.03 Prob>=chibar2 = 0.000
The output above indicates that the incident rate for 2.prog is 0.64 times the incident rate for the reference group (1.prog). Likewise, the incident rate for 3.prog is 0.28 times the incident rate for the reference group holding the other variables constant. The percent change in the incident rate of daysabs is a 1% decrease for every unit increase in math.
The form of the model equation for negative binomial regression is the same as that for Poisson regression. The log of the outcome is predicted with a linear combination of the predictors:
log(daysabs) = Intercept + b1(prog=2) + b2(prog=3) + b3math.
This implies:
daysabs = exp(Intercept + b1(prog=2) + b2(prog=3)+ b3math) = exp(Intercept) * exp(b1(prog=2)) * exp(b2(prog=3)) * exp(b3math)
The coefficients have an additive effect in the log(y) scale and the IRR have a multiplicative effect in the y scale. The dispersion parameter alpha in negative binomial regression does not effect the expected counts, but it does effect the estimated variance of the expected counts. More details can be found in the Stata documentation.
For additional information on the various metrics in which the results can be presented, and the interpretation of such, please see Regression Models for Categorical Dependent Variables Using Stata, Second Edition by J. Scott Long and Jeremy Freese (2006).
To understand the model better, we can use the margins command. Below we use the margins command to calculate the predicted counts at each level of prog, holding all other variables (in this example, math) in the model at their means.
margins prog, atmeans Adjusted predictions Number of obs = 314 Model VCE : OIM Expression : Predicted number of events, predict() at : math = 48.26752 (mean) 1.prog = .1273885 (mean) 2.prog = .5318471 (mean) 3.prog = .3407643 (mean) ------------------------------------------------------------------------------ | Delta-method | Margin Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- prog | 1 | 10.2369 1.674445 6.11 0.000 6.955048 13.51875 2 | 6.587927 .5511718 11.95 0.000 5.50765 7.668204 3 | 2.850083 .3296496 8.65 0.000 2.203981 3.496184 ------------------------------------------------------------------------------
In the output above, we see that the predicted number of events for level 1 of prog is about 10.24, holding math at its mean. The predicted number of events for level 2 of prog is lower at 6.59, and the predicted number of events for level 3 of prog is about 2.85. Note that the predicted count of level 2 of prog is (6.587927/10.2369) = 0.64 times the predicted count for level 1 of prog. This matches what we saw in the IRR output table.
Below we will obtain the predicted number of events for values of math that range from 0 to 100 in increments of 20.
margins, at(math=(0(20)100)) vsquish Predictive margins Number of obs = 314 Model VCE : OIM Expression : Predicted number of events, predict() 1._at : math = 0 2._at : math = 20 3._at : math = 40 4._at : math = 60 5._at : math = 80 6._at : math = 100 ------------------------------------------------------------------------------ | Delta-method | Margin Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _at | 1 | 7.717607 .9993707 7.72 0.000 5.758876 9.676337 2 | 6.845863 .6132453 11.16 0.000 5.643924 8.047802 3 | 6.072587 .3986397 15.23 0.000 5.291268 6.853907 4 | 5.386657 .4039343 13.34 0.000 4.59496 6.178354 5 | 4.778206 .5226812 9.14 0.000 3.75377 5.802643 6 | 4.238483 .6474951 6.55 0.000 2.969416 5.50755 ------------------------------------------------------------------------------
The table above shows that with prog at its observed values and math held at 0 for all observations, the average predicted count (or average number of days absent) is about 7.72; when math = 100, the average predicted count is about 4.24. If we compare the predicted counts at any two levels of math, like math = 20 and math = 40, we can see that the ratio is (6.072587/6.845863) = 0.887. This matches the IRR of 0.994 for a 20 unit change: 0.994^20 = 0.887.
The user-written fitstat command (as well as Stata’s estat commands) can be used to obtain additional model fit information that may be helpful if you want to compare models. You can type search fitstat to download this program (see How can I use the search command to search for programs and get additional help? for more information about using search).
fitstatMeasures of Fit for nbreg of daysabs Log-Lik Intercept Only: -896.472 Log-Lik Full Model: -865.629 D(308): 1731.258 LR(3): 61.687 Prob > LR: 0.000 McFadden's R2: 0.034 McFadden's Adj R2: 0.028 ML (Cox-Snell) R2: 0.178 Cragg-Uhler(Nagelkerke) R2: 0.179 AIC: 5.552 AIC*n: 1743.258 BIC: -39.555 BIC': -44.439 BIC used by Stata: 1760.005 AIC used by Stata: 1741.258
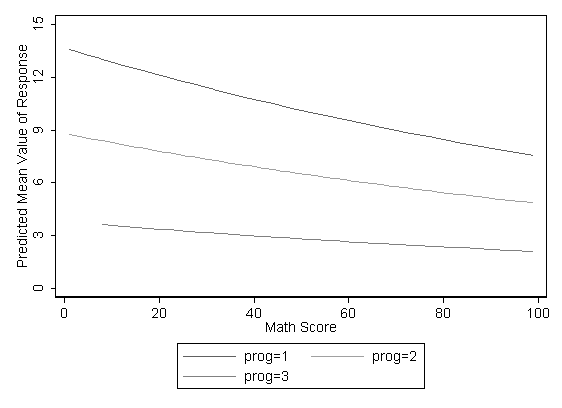
You can graph the predicted number of events with the commands below. The graph indicates that the most days absent are predicted for those in the academic program 1, especially if the student has a low math score. The lowest number of predicted days absent is for those students in program 3.
predict c
sort math
twoway (line c math if prog==1) ///
(line c math if prog==2) ///
(line c math if prog==3), ///
ytitle("Predicted Mean Value of Response") ylabel(0(3)15 ,nogrid) ///
xtitle("Math Score") legend(order(1 "prog=1" 2 "prog=2" 3 "prog=3")) scheme(s1mono)
Things to consider
- It is not recommended that negative binomial models be applied to small samples.
- One common cause of over-dispersion is excess zeros by an additional data generating process. In this situation, zero-inflated model should be considered.
- If the data generating process does not allow for any 0s (such as the number of days spent in the hospital), then a zero-truncated model may be more appropriate.
- Count data often have an exposure variable, which indicates the number of times the event could have happened. This variable should be incorporated into your negative binomial regression model with the use of the exp() option.
- The outcome variable in a negative binomial regression cannot have negative numbers, and the exposure cannot have 0s.
- You can also run a negative binomial model using the glm command with the log link and the binomial family.
- You will need to use the glm command to obtain the residuals to check other assumptions of the negative binomial model (see Cameron and Trivedi (1998) and Dupont (2002) for more information).
- Pseudo-R-squared: Many different measures of pseudo-R-squared exist. They all attempt to provide information similar to that provided by R-squared in OLS regression; however, none of them can be interpreted exactly as R-squared in OLS regression is interpreted. For a discussion of various pseudo-R-squares, see Long and Freese (2006) or our FAQ page What are pseudo R-squareds? .
See also
- Annotated output for the nbreg command
- Stata online manual
- Related Stata commands
- poisson — poisson regression
- Stata FAQs
References
- Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
- Long, J. S. and Freese, J. (2006). Regression Models for Categorical Dependent Variables Using Stata, Second Edition. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. (2009). Microeconometrics Using Stata. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. (1998). Regression Analysis of Count Data. New York: Cambridge Press.
- Cameron, A. C. Advances in Count Data Regression Talk for the Applied Statistics Workshop, March 28, 2009. http://cameron.econ.ucdavis.edu/racd/count.html .
- Dupont, W. D. (2002). Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data. New York: Cambridge Press.