Version info: Code for this page was tested in Stata 12.
Multinomial logistic regression is used to model nominal outcome variables, in which the log odds of the outcomes are modeled as a linear combination of the predictor variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics and potential follow-up analyses.
Examples of multinomial logistic regression
Example 1. People’s occupational choices might be influenced by their parents’ occupations and their own education level. We can study the relationship of one’s occupation choice with education level and father’s occupation. The occupational choices will be the outcome variable which consists of categories of occupations.
Example 2. A biologist may be interested in food choices that alligators make. Adult alligators might have different preferences from young ones. The outcome variable here will be the types of food, and the predictor variables might be size of the alligators and other environmental variables.
Example 3. Entering high school students make program choices among general program, vocational program and academic program. Their choice might be modeled using their writing score and their social economic status.
Description of the data
For our data analysis example, we will expand the third example using the hsbdemo data set. Let’s first read in the data.
use https://stats.idre.ucla.edu/stat/data/hsbdemo, clear
The data set contains variables on 200 students. The outcome variable is prog, program type. The predictor variables are social economic status, ses, a three-level categorical variable and writing score, write, a continuous variable. Let’s start with getting some descriptive statistics of the variables of interest.
tab prog ses, chi2 type of | ses program | low middle high | Total -----------+---------------------------------+---------- general | 16 20 9 | 45 academic | 19 44 42 | 105 vocation | 12 31 7 | 50 -----------+---------------------------------+---------- Total | 47 95 58 | 200 Pearson chi2(4) = 16.6044 Pr = 0.002table prog, con(mean write sd write) ------------------------------------ type of | program | mean(write) sd(write) ----------+------------------------- general | 51.33333 9.397776 academic | 56.25714 7.943343 vocation | 46.76 9.318754 ------------------------------------
Analysis methods you might consider
- Multinomial logistic regression: the focus of this page.
- Multinomial probit regression: similar to multinomial logistic regression but with independent normal error terms.
- Multiple-group discriminant function analysis: A multivariate method for multinomial outcome variables
- Multiple logistic regression analyses, one for each pair of outcomes: One problem with this approach is that each analysis is potentially run on a different sample. The other problem is that without constraining the logistic models, we can end up with the probability of choosing all possible outcome categories greater than 1.
- Collapsing number of categories to two and then doing a logistic regression: This approach suffers from loss of information and changes the original research questions to very different ones.
- Ordinal logistic regression: If the outcome variable is truly ordered and if it also satisfies the assumption of proportional odds, then switching to ordinal logistic regression will make the model more parsimonious.
- Alternative-specific multinomial probit regression: allows different error structures therefore allows to relax the independence of irrelevant alternatives (IIA, see below “Things to Consider”) assumption. This requires that the data structure be choice-specific.
- Nested logit model: also relaxes the IIA assumption, also requires the data structure be choice-specific.
Multinomial logistic regression
Below we use the mlogit command to estimate a multinomial logistic regression model. The i. before ses indicates that ses is a indicator variable (i.e., categorical variable), and that it should be included in the model. We have also used the option “base” to indicate the category we would want to use for the baseline comparison group. In the model below, we have chosen to use the academic program type as the baseline category.
mlogit prog i.ses write, base(2)
Iteration 0: log likelihood = -204.09667
Iteration 1: log likelihood = -180.80105
Iteration 2: log likelihood = -179.98724
Iteration 3: log likelihood = -179.98173
Iteration 4: log likelihood = -179.98173
Multinomial logistic regression Number of obs = 200
LR chi2(6) = 48.23
Prob > chi2 = 0.0000
Log likelihood = -179.98173 Pseudo R2 = 0.1182
------------------------------------------------------------------------------
prog | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
ses |
2 | -.533291 .4437321 -1.20 0.229 -1.40299 .336408
3 | -1.162832 .5142195 -2.26 0.024 -2.170684 -.1549804
|
write | -.0579284 .0214109 -2.71 0.007 -.0998931 -.0159637
_cons | 2.852186 1.166439 2.45 0.014 .5660075 5.138365
-------------+----------------------------------------------------------------
academic | (base outcome)
-------------+----------------------------------------------------------------
vocation |
ses |
2 | .2913931 .4763737 0.61 0.541 -.6422822 1.225068
3 | -.9826703 .5955669 -1.65 0.099 -2.14996 .1846195
|
write | -.1136026 .0222199 -5.11 0.000 -.1571528 -.0700524
_cons | 5.2182 1.163549 4.48 0.000 2.937686 7.498714
------------------------------------------------------------------------------
- In the output above, we first see the iteration log, indicating how quickly the model converged. The log likelihood (-179.98173) can be usedin comparisons of nested models, but we won’t show an example of comparing models here
- The likelihood ratio chi-square of48.23 with a p-value < 0.0001 tells us that our model as a whole fits significantly better than an empty model (i.e., a model with no predictors)
- The output above has two parts, labeled with the categories of the
outcome variable prog. They correspond to the two equations below:
$$ln\left(\frac{P(prog=general)}{P(prog=academic)}\right) = b_{10} + b_{11}(ses=2) + b_{12}(ses=3) + b_{13}write$$
$$ln\left(\frac{P(prog=vocation)}{P(prog=academic)}\right) = b_{20} + b_{21}(ses=2) + b_{22}(ses=3) + b_{23}write$$
where \(b\)’s are the regression coefficients.
- A one-unit increase in the variable write is associated with a .058 decrease in the relative log odds of being in general program vs. academic program .
- A one-unit increase in the variable write is associated with a .1136 decrease in the relative log odds of being in vocation program vs. academic program.
- The relative log odds of being in general program vs. in academic program will decrease by 1.163 if moving from the lowest level of ses (ses==1) to the highest level of ses (ses==3).
The ratio of the probability of choosing one outcome category over the probability of choosing the baseline category is often referred to as relative risk (and it is also sometimes referred to as odds as we have just used to described the regression parameters above). Relative risk can be obtained by exponentiating the linear equations above, yielding regression coefficients that are relative risk ratios for a unit change in the predictor variable. We can use the rrr option for mlogit command to display the regression results in terms of relative risk ratios.
mlogit, rrr
Multinomial logistic regression Number of obs = 200
LR chi2(6) = 48.23
Prob > chi2 = 0.0000
Log likelihood = -179.98173 Pseudo R2 = 0.1182
------------------------------------------------------------------------------
prog | RRR Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
general |
ses |
2 | .586671 .2603248 -1.20 0.229 .2458607 1.39991
3 | .3125996 .1607448 -2.26 0.024 .1140996 .856432
|
write | .9437175 .0202059 -2.71 0.007 .9049342 .984163
_cons | 17.32562 20.20928 2.45 0.014 1.761221 170.4369
-------------+----------------------------------------------------------------
academic | (base outcome)
-------------+----------------------------------------------------------------
vocation |
ses |
2 | 1.338291 .6375264 0.61 0.541 .5260904 3.404399
3 | .3743103 .2229268 -1.65 0.099 .1164888 1.202761
|
write | .8926126 .0198338 -5.11 0.000 .8545734 .9323449
_cons | 184.6016 214.793 4.48 0.000 18.87213 1805.719
------------------------------------------------------------------------------
- The relative risk ratio for a one-unit increase in the variable write is .9437 (exp(-.0579284) from the output of the first mlogit command above) for being in general program vs. academic program.
- The relative risk ratio switching from ses = 1 to 3 is .3126 for being in general program vs. academic program. In other words, the expected risk of staying in the general program is lower for subjects who are high in ses.
We can test for an overall effect of ses using the test command. Below we see that the overall effect of ses is statistically significant.
test 2.ses 3.ses
( 1) [general]2.ses = 0
( 2) [academic]2.ses = 0
( 3) [vocation]2.ses = 0
( 4) [general]3.ses = 0
( 5) [academic]3.ses = 0
( 6) [vocation]3.ses = 0
Constraint 2 dropped
Constraint 5 dropped
chi2( 4) = 10.82
Prob > chi2 = 0.0287
More specifically, we can also test if the effect of 3.ses in predicting general vs. academic equals the effect of 3.ses in predicting vocation vs. academic using the test command again. The test shows that the effects are not statistically different from each other.
test [general]3.ses = [vocation]3.ses
( 1) [general]3.ses - [vocation]3.ses = 0
chi2( 1) = 0.08
Prob > chi2 = 0.7811
You can also use predicted probabilities to help you understand the model. You can calculate predicted probabilities using the margins command. Below we use the margins command to calculate the predicted probability of choosing each program type at each level of ses, holding all other variables in the model at their means. Since there are three possible outcomes, we will need to use the margins command three times, one for each outcome value.
margins ses, atmeans predict(outcome(1))
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==general), predict(outcome(1))
at : 1.ses = .235 (mean)
2.ses = .475 (mean)
3.ses = .29 (mean)
write = 52.775 (mean)
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ses |
1 | .3581927 .0726423 4.93 0.000 .2158163 .500569
2 | .2283338 .0451162 5.06 0.000 .1399075 .31676
3 | .1784932 .0540486 3.30 0.001 .0725598 .2844266
------------------------------------------------------------------------------
margins ses, atmeans predict(outcome(2))
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==academic), predict(outcome(2))
at : 1.ses = .235 (mean)
2.ses = .475 (mean)
3.ses = .29 (mean)
write = 52.775 (mean)
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ses |
1 | .4396842 .0779925 5.64 0.000 .2868217 .5925466
2 | .4777488 .0552593 8.65 0.000 .3694426 .586055
3 | .7009021 .0663042 10.57 0.000 .5709483 .8308559
------------------------------------------------------------------------------
margins ses, atmeans predict(outcome(3))
Adjusted predictions Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==vocation), predict(outcome(3))
at : 1.ses = .235 (mean)
2.ses = .475 (mean)
3.ses = .29 (mean)
write = 52.775 (mean)
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
ses |
1 | .2021232 .0599647 3.37 0.001 .0845945 .3196519
2 | .2939174 .0503617 5.84 0.000 .1952103 .3926246
3 | .1206047 .04643 2.60 0.009 .0296037 .2116058
------------------------------------------------------------------------------
We can use the marginsplot command to plot predicted probabilities by ses for each category of prog. Plots created by marginsplot are based on the last margins command run. Furthermore, we can combine the three marginsplots into one graph to facilitate comparison using the graph combine command. As it is generated, each marginsplot must be given a name, which will be used by graph combine. Additionally, we would like the y-axes to have the same range, so we use the ycommon option with graph combine .
margins ses, atmeans predict(outcome(1)) marginsplot, name(general) margins ses, atmeans predict(outcome(2)) marginsplot, name(academic) margins ses, atmeans predict(outcome(3)) marginsplot, name(vocational) graph combine general academic vocational, ycommon
Another way to understand the model using the predicted probabilities is to look at the averaged predicted probabilities for different values of the continuous predictor variable write, averaging across levels of ses.
margins, at(write = (30(10) 70)) predict(outcome(1)) vsquish
Predictive margins Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==general), predict(outcome(1))
1._at : write = 30
2._at : write = 40
3._at : write = 50
4._at : write = 60
5._at : write = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | .2130954 .0774327 2.75 0.006 .0613302 .3648606
2 | .2569932 .0529761 4.85 0.000 .1531619 .3608245
3 | .2543008 .0336297 7.56 0.000 .1883878 .3202138
4 | .2057855 .0371536 5.54 0.000 .1329658 .2786052
5 | .1423089 .0481683 2.95 0.003 .0479007 .2367172
------------------------------------------------------------------------------
margins, at(write = (30(10) 70)) predict(outcome(2)) vsquish
Predictive margins Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==academic), predict(outcome(2))
1._at : write = 30
2._at : write = 40
3._at : write = 50
4._at : write = 60
5._at : write = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | .1348408 .0525979 2.56 0.010 .0317507 .2379308
2 | .2808143 .0553213 5.08 0.000 .1723867 .389242
3 | .4773283 .0397591 12.01 0.000 .399402 .5552547
4 | .6680752 .0434689 15.37 0.000 .5828776 .7532727
5 | .8075124 .0545504 14.80 0.000 .7005956 .9144291
------------------------------------------------------------------------------
margins, at(write = (30(10) 70)) predict(outcome(3)) vsquish
Predictive margins Number of obs = 200
Model VCE : OIM
Expression : Pr(prog==vocation), predict(outcome(3))
1._at : write = 30
2._at : write = 40
3._at : write = 50
4._at : write = 60
5._at : write = 70
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | .6520638 .0944041 6.91 0.000 .4670353 .8370924
2 | .4621925 .0614388 7.52 0.000 .3417747 .5826102
3 | .2683708 .0342932 7.83 0.000 .2011575 .3355842
4 | .1261393 .03019 4.18 0.000 .0669679 .1853107
5 | .0501787 .0216863 2.31 0.021 .0076744 .092683
------------------------------------------------------------------------------
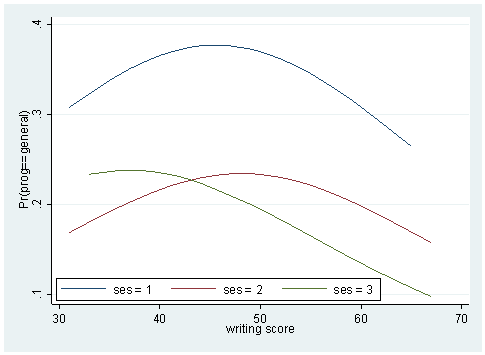
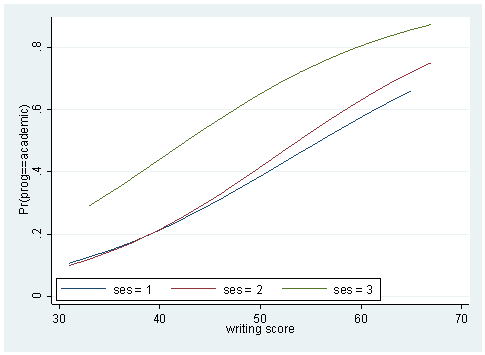
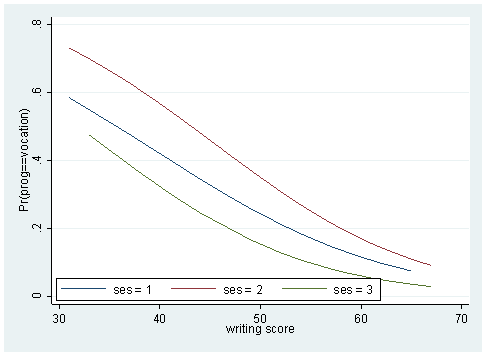
Sometimes, a couple of plots can convey a good deal amount of information. Below, we plot the predicted probabilities against the writing score by the level of ses for different levels of the outcome variable.
predict p1 p2 p3 sort write twoway (line p1 write if ses ==1) (line p1 write if ses==2) (line p1 write if ses ==3), /// legend(order(1 "ses = 1" 2 "ses = 2" 3 "ses = 3") ring(0) position(7) row(1)) twoway (line p2 write if ses ==1) (line p2 write if ses==2) (line p2 write if ses ==3), /// legend(order(1 "ses = 1" 2 "ses = 2" 3 "ses = 3") ring(0) position(7) row(1)) twoway (line p3 write if ses ==1) (line p3 write if ses==2) (line p3 write if ses ==3), /// legend(order(1 "ses = 1" 2 "ses = 2" 3 "ses = 3") ring(0) position(7) row(1))
We may also wish to see measures of how well our model fits. This can be particularly useful when comparing competing models. The user-written command fitstat produces a variety of fit statistics. You can find more information on fitstat and download the program by using command search fitstat in Stata (see How can I use the search command to search for programs and get additional help? for more information about using search).
fitstat
Measures of Fit for mlogit of prog
fit
Log-Lik Intercept Only: -204.097 Log-Lik Full Model: -179.982
D(185): 359.963 LR(6): 48.230
Prob > LR: 0.000
McFadden's R2: 0.118 McFadden's Adj R2: 0.045
ML (Cox-Snell) R2: 0.214 Cragg-Uhler(Nagelkerke) R2: 0.246
Count R2: 0.610 Adj Count R2: 0.179
AIC: 1.950 AIC*n: 389.963
BIC: -620.225 BIC': -16.440
BIC used by Stata: 402.350 AIC used by Stata: 375.963
Things to consider
- The Independence of Irrelevant Alternatives (IIA) assumption: roughly, the IIA assumption means that adding or deleting alternative outcome categories does not affect the odds among the remaining outcomes. Test of the IIA assumption can be performed by using the Stata command mlogtest, iia. However, as of April 23, 2010, mlogtest, iia does not work with factor variables. There are alternative modeling methods that relax the IIA assumption, such as alternative-specific multinomial probit models or nested logit models.
- Diagnostics and model fit: unlike logistic regression where there are many statistics for performing model diagnostics, it is not as straightforward to do diagnostics with multinomial logistic regression models. Model fit statistics can be obtained via the fitstat command. For the purpose of detecting outliers or influential data points, one can run separate logit models and use the diagnostics tools on each model.
- Pseudo-R-Squared: the R-squared offered in the output is basically the change in terms of log-likelihood from the intercept-only model to the current model. It does not convey the same information as the R-square for linear regression, even though it is still “the higher, the better”.
- Sample size: multinomial regression uses a maximum likelihood estimation method, it requires a large sample size. It also uses multiple equations. This implies that it requires an even larger sample size than ordinal or binary logistic regression.
- Complete or quasi-complete separation: Complete separation implies that the outcome variable separates a predictor variable completely, leading to perfect prediction by the predictor variable. Unlike running a logit model, Stata does not offer a warning when this happens. Instead it continues to compute iteratively and requires a manual quit to stop the process. Perfect prediction means that only one value of a predictor variable is associated with only one value of the response variable. But you can tell from the output of the regression coefficients that something is wrong. You can then do a two-way tabulation of the outcome variable with the problematic variable to confirm this and then rerun the model without the problematic variable.
- Empty cells or small cells: You should check for empty or small cells by doing a cross-tabulation between categorical predictors and the outcome variable. If a cell has very few cases (a small cell), the model may become unstable or it might not even run at all.
- Perhaps your data may not perfectly meet the assumptions and your standard errors might be off the mark. You might wish to see our page that shows alternative methods for computing standard errors that Stata offers.
- Sometimes observations are clustered into groups (e.g., people within families, students within classrooms). In such cases, you may want to see our page on non-independence within clusters.
See also
References
- Long, J. S. and Freese, J. (2006) Regression Models for Categorical and Limited Dependent Variables Using Stata, Second Edition. College Station, Texas: Stata Press.
- Hosmer, D. and Lemeshow, S. (2000) Applied Logistic Regression (Second Edition). New York: John Wiley & Sons, Inc..
- Agresti, A. (1996) An Introduction to Categorical Data Analysis. New York: John Wiley & Sons, Inc.