The Stata command sureg runs a seemingly unrelated regression (SUR). That is a regression in which two (or more) unrelated outcome variables are predicted by sets of predictor variables. These predictor variables may or may not be the same for the two outcomes. If the set of predictor variables is identical across the two outcomes, the results from sureg will be identical to those from OLS. In other cases (i.e. non-identical prediction equations), SUR produces more efficient estimates than OLS. It does this by weighting the estimates by the covariance of the residuals from the individual regressions. See Greene (2005 p 340-351) for additional information on seemingly unrelated regression. Below we show how to replicate the results of Stata’s sureg command.
We will fit the following model:
read = b_0 + b_1*math + b_2*write + b_3*socst + e_r science = g_0 + g_1*female + g_2*math + e_s
The coefficients b_0, b_1, b_2, and b_3, are the intercept and regression coefficients for read, and e_r is the error term for read. The coefficients g_0, g_1, and g_2 are the regression coefficients for science, and e_s is the error term for science.
The matrix form of the equation for these coefficients is:
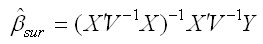
Where X is a matrix of predictors, Y is a vector of outcomes, and V is:
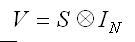
that is the Kronecker product of S and I. Where S is the variance covariance matrix of OLS residuals and I is an identity matrix of size n equal to the number of cases in the analysis.
Below we open the dataset and then run the above model using the sureg command.
use https://stats.idre.ucla.edu/stat/data/hsb2, clear
sureg (read math write socst) (science female math)
Seemingly unrelated regression
----------------------------------------------------------------------
Equation Obs Parms RMSE "R-sq" chi2 P
----------------------------------------------------------------------
read 200 3 6.884452 0.5469 234.17 0.0000
science 200 2 7.591249 0.4092 137.41 0.0000
----------------------------------------------------------------------
------------------------------------------------------------------------------
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
read |
math | .4820974 .0676596 7.13 0.000 .3494869 .6147079
write | .1112919 .0692286 1.61 0.108 -.0243936 .2469775
socst | .2775624 .0570989 4.86 0.000 .1656506 .3894741
_cons | 6.430895 3.096425 2.08 0.038 .3620135 12.49978
-------------+----------------------------------------------------------------
science |
female | -1.687415 1.045627 -1.61 0.107 -3.736806 .3619758
math | .663942 .0574353 11.56 0.000 .5513709 .7765132
_cons | 17.81641 3.139002 5.68 0.000 11.66408 23.96874
------------------------------------------------------------------------------
We will use the regress command to predict read using write, math, and socst. After we run the regression we use predict to create a new variable r_resid which contains the residual for each case. Further below we repeat the last two steps for the model predicting science.
regress read write math socst predict r_read, resid regress science female math predict r_sci, resid
We use the cor (correlate) command with the cov option to obtain the covariance matrix for the residuals from the above regressions. We store this matrix as s, a 2 by 2 symmetric matrix. Then we create another matrix i, which is an identity matrix with the number of rows and columns equal to the number of cases in the analysis, i.e., i is a 200 by 200 identity matrix. Finally, the matrix v is the Kronecker product of s and i resulting in a 400 by 400 matrix.
cor r_read r_sci, cov mat s = r(C) mat i = I(200) mat v = s#i gen cons = 1
Below is an example of what the X matrix should look like when we are done. The first two lines of the matrix shown below are the lines for the first equation (with additional cases omitted), the second set of lines shows the lines for the second equation. Note that the math scores are the same, since the same two hypothetical cases are shown.
math write socst cons female math cons
53 45 62 1 0 0 0
46 53 58 1 0 0 0
...
0 0 0 0 1 53 1
0 0 0 0 0 46 1
...
The code below takes the values of the predictor variables for the first equation (i.e., math write socst cons) from the dataset and places them in a matrix, x_read. In the second line of code below a matrix of zeros produced by the function J(200,3,0) with 200 rows (n=200) and 3 columns (for three variables in the second equation) is placed to the right of the values from the dataset. A similar process takes place for the predictors from the second equation (x_sci) except this time the matrix of zeros is 200 by 4, and is placed to the left of the values from the dataset. The final line of code below stacks the matrix for the first equation (x_read) on top of the matrix for the second equation (x_sci), creating a single matrix x, with 400 rows and 7 columns.
mkmat math write socst cons, matrix(x_read) mat x_read = x_read , J(200,3,0) mkmat female math cons, matrix(x_sci) mat x_sci = J(200,4,0) , x_sci mat x = x_read \x_sci
First two vectors are created, one for each of the two dependent variables (read and science), then the vector of read values is stacked on top of the vector of science values to create a single vector y with 400 rows.
mkmat read, matrix(y_read) mkmat science, matrix(y_sci) mat y = y_read \y_sci
Finally we compute the weighted estimates, producing the vector b with 7 rows. Then we can list the vector to look at our parameter estimates. Note that these are the same as the coefficient estimates produced by sureg.
mat b = inv(x'*inv(v)*x)*x'*inv(v)*y
mat list b
b[7,1]
read
math .4820974
write .11129194
socst .27756235
cons 6.4308952
c1 -1.687415
c2 .66394202
c3 17.816414
Using Mata
For the relatively small example above, we could use Stata’s matrix functions to reproduce the estimates from the sureg. However, if you wanted to do this with a larger example, you might need to use Mata. Below is the code to reproduce the same example using Stata and Mata.
use https://stats.idre.ucla.edu/stat/data/hsb2, clear sureg (read math write socst) (science female math) * run both models and get residuals reg read math write socst predict r_read, resid reg science female math predict r_sci, resid * create variable to act as constant in regressions capture gen cons = 1 * get the covariance between the residuals cor r_read r_sci, cov mata: /* calculate v the weight matrix based on the error covariances */ s = st_matrix("r(C)") i = I(200) v = s#i /* matrix for x variables for read (plus appropriate zeros) */ x_read = st_data(.,("math", "write", "socst", "cons")) x_read = x_read , J(200,3,0) /* matrix for x variables for science (prefixed by the appropriate zeros) */ x_sci = st_data(.,("female", "math", "cons")) x_sci = J(200,4,0) , x_sci /* Stack matrix for first equation on top of matrix for second equation */ x = x_read \ x_sci /* vectors for each of the y variables, stack read on top of science */ y = st_data(.,"read") \ st_data(.,"science") /* calculate the estimates and post them back to the Stata matrix b */ b = qrinv(x'*luinv(v)*x)*x'*luinv(v)*y st_matrix("b",b) endmat li b0 b0[1,7] read: read: read: read: science: science: science: math write socst _cons female math _cons y1 .4820974 .11129194 .27756235 6.4308952 -1.687415 .66394202 17.816414 mat li b1 b1[1,7] c1 c2 c3 c4 c5 c6 c7 r1 .4820974 .11129194 .27756235 6.4308952 -1.687415 .66394202 17.816414
References
Greene, William H. (2005). Econometric Analysis. Fifth edition. Pearson Education.
See also
Stata FAQ: What is seemingly unrelated regression and how can I perform it in Stata?
