Version info: Code for this page was tested in IBM SPSS 20.
Linear discriminant function analysis (i.e., discriminant analysis) performs a multivariate test of differences between groups. In addition, discriminant analysis is used to determine the minimum number of dimensions needed to describe these differences. A distinction is sometimes made between descriptive discriminant analysis and predictive discriminant analysis. We will be illustrating predictive discriminant analysis on this page.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of discriminant function analysis
Example 1. A large international air carrier has collected data on employees in three different job classifications: 1) customer service personnel, 2) mechanics and 3) dispatchers. The director of Human Resources wants to know if these three job classifications appeal to different personality types. Each employee is administered a battery of psychological test which include measures of interest in outdoor activity, sociability and conservativeness.
Example 2.
There is Fisher’s (1936) classic example of discriminant analysis involving three varieties of iris and four predictor variables (petal width, petal length, sepal width, and sepal length). Fisher not only wanted to determine if the varieties differed significantly on the four continuous variables, but he was also interested in predicting variety classification for unknown individual plants.
Description of the data
Let’s pursue Example 1 from above.
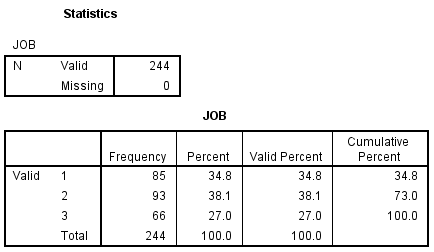
We have included the data file, which can be obtained by clicking on discrim.sav. The dataset has 244 observations on four variables. The psychological variables are outdoor interests, social and conservative. The categorical variable is job type with three levels; 1) customer service, 2) mechanic, and 3) dispatcher.
Let’s look at the data. It is always a good idea to start with descriptive statistics.
get file='d:\data\discrim.sav' . descriptives variables=outdoor social conservative.means tables=outdoor social conservative by job.
correlations variables=outdoor social conservative.
frequencies variables=job.
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Discriminant function analysis – This procedure is multivariate and also provides information on the individual dimensions.
- MANOVA – The tests of significance are the same as for discriminant function analysis, but MANOVA gives no information on the individual dimensions.
- Multinomial logistic regression or multinomial probit – These are also viable options.
- Separate one-way ANOVAs – You could analyze these data using separate one-way ANOVAs for each psychological variable. The separate ANOVAs will not produce multivariate results and do not report information concerning dimensionality. Again, the designation of independent and dependent variables is reversed as in MANOVA.
Discriminant function analysis
We will run the discriminant analysis using the discriminant procedure in SPSS.
There is a lot of output so we will comment at various places along the way.
discriminant /groups=job(1 3) /variables=outdoor social conservative /analysis all /priors equal /statistics=boxm table /plot=combined map /classify=pooled.
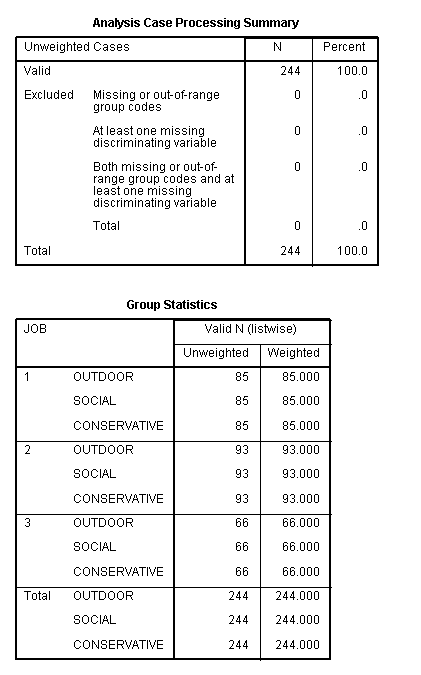
- The output above indicates that all 244 cases were used in the analysis.
- We also see the number of cases for each outcome variable at each level of the grouping variable.
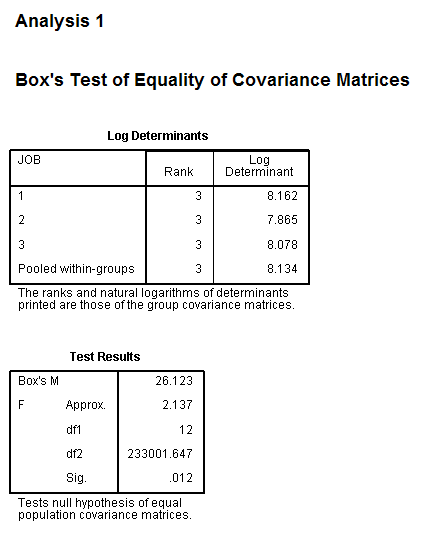
- Box’s test of equality of covariance matrices can be affected by deviations from multivariate normality.
- Note that the Standardized Canonical Discriminant Function Coefficients table and the Structure Matrix table are listed in different orders.
- The number of discriminant dimensions is the number of groups minus 1. However, some discriminant dimensions may not be statistically significant.
- In this example, there are two discriminant dimensions, both of which are statistically significant.
- The canonical correlations for the dimensions one and two are 0.72 and 0.49, respectively.
- The standardized discriminant coefficients function in a manner analogous to standardized regression coefficients in OLS regression. For example, a one standard deviation increase on the outdoor variable will result in a .32 standard deviation decrease in the predicted values on discriminant function 1.
- The canonical structure, also known as canonical loading or discriminant loadings, represent correlations between observed variables and the unobserved discriminant functions (dimensions).
- The discriminant functions are a kind of latent variable and the correlations are loadings analogous to factor loadings.
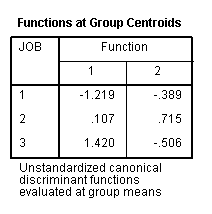
- Group centroids are the class (i.e., group) means of canonical variables.
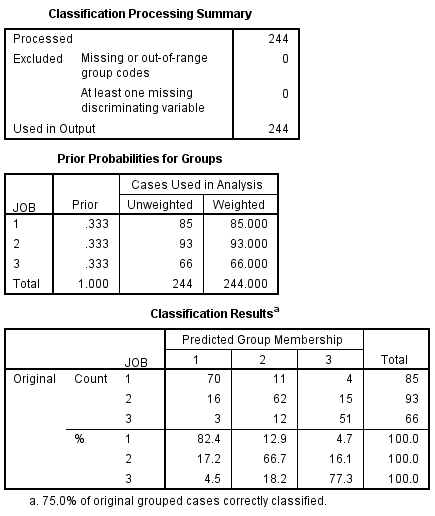
- The default is equal prior probabilities.
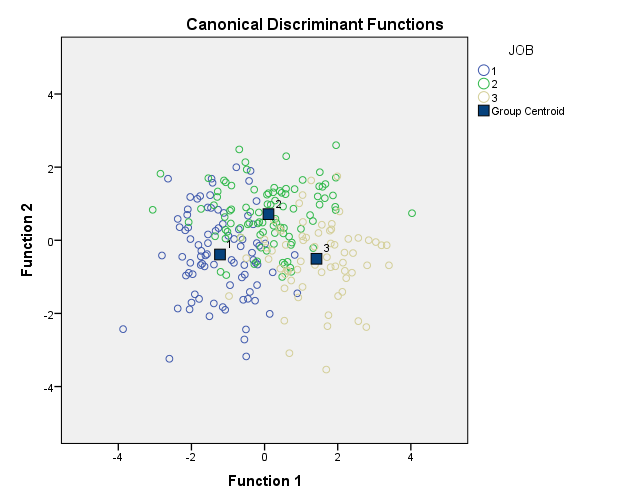
Next, we will plot a graph of individuals on the discriminant dimensions. Due to the large number of subjects we will shorten the labels for the job groups to make the graph more legible. As long as we don’t save the dataset these new labels will not be made permanent.
The discriminant functions are:
discriminant_score_1 = 0.517*conservative + 0.379*outdoor – 0.831*social.
discriminant_score_2 = 0.926*outdoor + 0.213*social – 0.291*conservative.
As you can see, the customer service employees tend to be at the more social (negative) end of dimension 1; the dispatchers tend to be at the opposite end, with the mechanics in the middle. On dimension 2 the results are not as clear; however, the mechanics tend to be higher on the outdoor dimension and customer service employees and dispatchers lower.
SPSS also produces an ASCII territorial map plot which shows the relative location of the boundaries of the different categories. The territorial map is shown below.
Territorial Map
Canonical Discriminant
Function 2
-6.0 -4.0 -2.0 .0 2.0 4.0 6.0
.............................................................
6.0 . 122 .
. 112 2.
. 12 223.
. 122 233 .
. 112 223 .
. 122 233 .
4.0 . 112 . . . . 223 .
. 12 233 .
. 122 223 .
. 112 2233 .
. 12 233 .
. 122 223 .
2.0 . . 112 . . 233 . .
. 122 223 .
. 112 233 .
. 12 223 .
. 122 * 233 .
. 112 223 .
.0 . . . 122. 233 . . .
. * 112 223 .
. 1233 * .
. 13 .
. 13 .
. 13 .
-2.0 . . . 13 . . .
. 13 .
. 13 .
. 13 .
. 13 .
. 13 .
-4.0 . . . 13 . . .
. 13 .
. 13 .
. 13 .
. 13 .
. 13 .
-6.0 . 13 .
.............................................................
-6.0 -4.0 -2.0 .0 2.0 4.0 6.0
Canonical Discriminant Function 1
Symbols used in territorial map
Symbol Group Label
------ ----- --------------------
1 1 customer service
2 2 mechanic
3 3 dispatch
* Indicates a group centroid
Things to consider
- Multivariate normal distribution assumptions holds for the response variables. This means that each of the dependent variables is normally distributed within groups, that any linear combination of the dependent variables is normally distributed, and that all subsets of the variables must be multivariate normal.
- Each group must have a sufficiently large number of cases.
- Different classification methods may be used depending on whether the variance-covariance matrices are equal (or very similar) across groups.
- Non-parametric discriminant function analysis, called kth nearest neighbor, can also be performed.
See also
References
- Grimm, L. G. and Yarnold, P. R. (editors). (1995). Reading and Understanding Multivariate Statistics. Washington, D.C.: American Psychological Association.
- Huberty, C. J. and Olejnik, S. (2006). Applied MANOVA and Discriminant Analysis, Second Edition. Hoboken, New Jersey: John Wiley and Sons, Inc.
- Stevens, J. P. (2002). Applied Multivariate Statistics for the Social Sciences, Fourth Edition. Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc.
- Tatsuoka, M. M. (1971). Multivariate Analysis: Techniques for Educational and Psychological Research. New York: John Wiley and Sons.