The hsb2 data set was used in this example, and the code used is given below. We first show the entire output; then we break the output into pieces and explain each part.
proc corr data = "D:\hsb2"; var read write math science female; run;
The CORR Procedure
5 Variables: read write math science female
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum Label
read 200 52.23000 10.25294 10446 28.00000 76.00000 reading score write 200 52.77500 9.47859 10555 31.00000 67.00000 writing score math 200 52.64500 9.36845 10529 33.00000 75.00000 math score science 200 51.85000 9.90089 10370 26.00000 74.00000 science score female 200 0.54500 0.49922 109.00000 0 1.00000
Pearson Correlation Coefficients, N = 200
Prob > |r| under H0: Rho=0
read write math science female
read 1.00000 0.59678 0.66228 0.63016 -0.05308 reading score <.0001 <.0001 <.0001 0.4553
write 0.59678 1.00000 0.61745 0.57044 0.25649 writing score <.0001 <.0001 <.0001 0.0002
math 0.66228 0.61745 1.00000 0.63073 -0.02934 math score <.0001 <.0001 <.0001 0.6801
science 0.63016 0.57044 0.63073 1.00000 -0.12774 science score <.0001 <.0001 <.0001 0.0714
female -0.05308 0.25649 -0.02934 -0.12774 1.00000
0.4553 0.0002 0.6801 0.0714
Summary statistics
5 Variablesa: read write math science female
Simple Statistics
Variablea Nb Meanc Std Devd Sume Minimumf Maximumf Labelg
read 200 52.23000 10.25294 10446 28.00000 76.00000 reading score write 200 52.77500 9.47859 10555 31.00000 67.00000 writing score math 200 52.64500 9.36845 10529 33.00000 75.00000 math score science 200 51.85000 9.90089 10370 26.00000 74.00000 science score female 200 0.54500 0.49922 109.00000 0 1.00000
a. Variable – This gives the list of variables that were used to create the correlation matrix. This is the same list as that on the var statement in proc corr code above.
b. N – This is the number of valid (i.e., non-missing) cases used in the correlation. In this example, all 200 students had scores for all tests. By default, proc corr uses pairwise deletion for missing observations, meaning that a pair of observations (one from each variable in the pair being correlated) is included if both values are non-missing. If you use the nomiss option on the proc corr statement, proc corr uses listwise deletion and omits all observations with missing data on any of the named variables.
c. Mean – This is the mean (or average) of the variable.
d. Std Dev – This is the standard deviation of the variable.
e. Sum – This is the sum of the variable. This is the value obtained if you added up all of the values for that variable.
f. Minimum and Maximum – These are the smallest and largest values of the variable, respectively.
g. Label – This is the label of the variable (the variable label). Variable labels are a form of data documentation and usually provide additional information about what the variable is.
The correlation matrix
Pearson Correlation Coefficientsh, N = 200i Prob > |r| under H0: Rho=0j
read write math science female
read 1.00000 0.59678 0.66228 0.63016 -0.05308 reading score <.0001 <.0001 <.0001 0.4553
write 0.59678 1.00000 0.61745 0.57044 0.25649 writing score <.0001 <.0001 <.0001 0.0002
math 0.66228 0.61745 1.00000 0.63073 -0.02934 math score <.0001 <.0001 <.0001 0.6801
science 0.63016 0.57044 0.63073 1.00000 -0.12774 science score <.0001 <.0001 <.0001 0.0714
female -0.05308 0.25649 -0.02934 -0.12774 1.00000
0.4553 0.0002 0.6801 0.0714
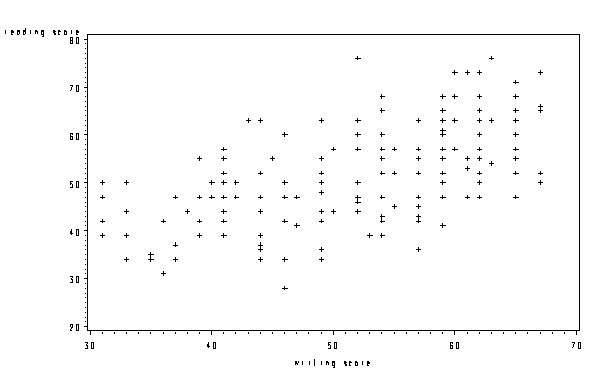
h. Pearson Correlation Coefficients – These numbers measure the strength and direction of the linear relationship between the two variables. The correlation coefficient can range from -1 to +1, with -1 indicating a perfect negative correlation, +1 indicating a perfect positive correlation, and 0 indicating no correlation at all. (A variable correlated with itself will always have a correlation coefficient of 1.) You can think of the correlation coefficient as telling you the extent to which you can guess the value of one variable given a value of the other variable. From the scatterplot of the variables read and write below, we can see that the points tend along a line going from the bottom left to the upper right, which is the same as saying that the correlation is positive. The .59678 is the numerical description of how tightly around the imaginary line the points lie. If the correlation was higher, the points would tend to be closer to the line; if it was smaller, they would tend to be further away from the line.
i. N = 200 – This indicates that 200 observations were used in the correlation of each pair of variables.
j. Prob > |r| under H0: Rho=0 – This is the p-value and indicates the probability of observing this correlation coefficient or one more extreme under the null hypothesis (H0) that the correlation (Rho) is 0.
NOTE: The heading for this section is constructed in this way so that you know that the top number is the correlation coefficient and the bottom number is the p-value. Also, you can use either continuous or dichotomous (e.g., 0/1) variables in a Pearson correlation, but you should not use multi-level categorical variables, for example, four categories of type of car. The correlation coefficient can be misleading if the range of the variable is restricted. For example, if the science test was too easy for most students, the upper range of the scale would be restricted and the correlation coefficient would not reflect the true correlation between science and the other variables.
Scatterplot
Below we show a scatterplot, which is the graphical version of a correlation. You can make a scatterplot matrix just like you can make a correlation matrix. This graph shows you the strength and direction of the relationship between the two variables just like the correlation coefficient.
proc gplot data = "D:\hsb2"; plot read*write; run; quit;