Robust regression is an alternative to least squares regression when data is contaminated with outliers or influential observations and it can also be used for the purpose of detecting influential observations.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
This page was developed using SAS 9.2.
Introduction
Let’s begin our discussion on robust regression with some terms in linear regression.
Residual: The difference between the predicted value (based on the regression equation) and the actual, observed value.
Outlier: In linear regression, an outlier is an observation with large residual. In other words, it is an observation whose dependent-variable value is unusual given its value on the predictor variables. An outlier may indicate a sample peculiarity or may indicate a data entry error or other problem.
Leverage: An observation with an extreme value on a predictor variable is a point with high leverage. Leverage is a measure of how far an independent variable deviates from its mean. High leverage points can have a great amount of effect on the estimate of regression coefficients.
Influence: An observation is said to be influential if removing the observation substantially changes the estimate of the regression coefficients. Influence can be thought of as the product of leverage and outlierness.
Cook’s distance (or Cook’s D): A measure that combines the information of leverage and residual of the observation.
Robust regression can be used in any situation in which you would use least squares regression. When fitting a least squares regression, we might find some outliers or high leverage data points. We have decided that these data points are not data entry errors, neither they are from a different population than most of our data. So we have no compelling reason to exclude them from the analysis. Robust regression might be a good strategy since it is a compromise between excluding these points entirely from the analysis and including all the data points and treating all them equally in OLS regression. The idea of robust regression is to weigh the observations differently based on how well behaved these observations are. Roughly speaking, it is a form of weighted and reweighted least squares regression.
Proc robustreg in SAS command implements several versions of robust regression. In this page, we will show M-estimation with Huber and bisquare weighting. These two are very standard and are combined as the default weighting function in Stata’s robust regression command. In Huber weighting, observations with small residuals get a weight of 1 and the larger the residual, the smaller the weight. With bisquare weighting, all cases with a non-zero residual get down-weighted at least a little.
Description of the example data
For our data analysis below, we will use the data set crime. This dataset appears in Statistical Methods for Social Sciences, Third Edition by Alan Agresti and Barbara Finlay (Prentice Hall, 1997). The variables are state id (sid), state name (state), violent crimes per 100,000 people (crime), murders per 1,000,000 (murder), the percent of the population living in metropolitan areas (pctmetro), the percent of the population that is white (pctwhite), percent of population with a high school education or above (pcths), percent of population living under poverty line (poverty), and percent of population that are single parents (single). It has 51 observations. We are going to use poverty and single to predict crime.
data crime; infile "crime.csv" delimiter="," firstobs=2; input sid state $ crime murder pctmetro pctwhite pcths poverty single; run; proc means data = crime; var crime poverty single; run; The MEANS Procedure Variable N Mean Std Dev Minimum Maximum ------------------------------------------------------------------------------ crime 51 612.8431373 441.1003229 82.0000000 2922.00 poverty 51 14.2588235 4.5842415 8.0000000 26.4000000 single 51 11.3254902 2.1214941 8.4000000 22.1000000 ------------------------------------------------------------------------------
Using robust regression analysis
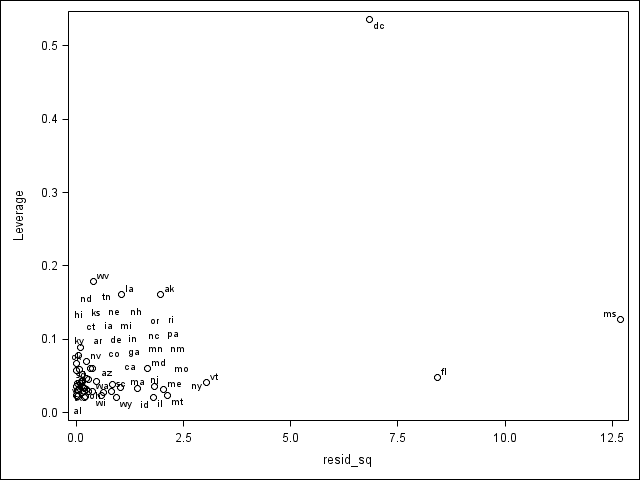
In most cases, we begin by running an OLS regression and doing some diagnostics. We will begin by running an OLS regression. We create a graph showing the leverage versus the squared residuals, labeling the points with the state abbreviations. To do so, we output the residuals and leverage in proc reg (along with Cook’s-D, which we will use later).
proc reg data = crime; model crime = poverty single ; output out = t student=res cookd = cookd h = lev; run; quit; data t; set t; resid_sq = res*res; run; proc sgplot data = t; scatter y = lev x = resid_sq / datalabel = state; run; quit;
As we can see, DC, Florida and Mississippi have either high leverage or large residuals. We can display the observations that have relatively large values of Cook’s D. A conventional cut-off point is 4/n, where n is the number of observations in the data set. We will use this criterion to select the values to display.
proc print data = t; where cookd > 4/51; var state crime poverty single cookd; run; Obs state crime poverty single cookd 1 ak 761 9.1 14.3 0.12547 9 fl 1206 17.8 10.6 0.14259 25 ms 434 24.7 14.7 0.61387 51 dc 2922 26.4 22.1 2.63625
We probably should drop DC to begin with since it is not even a state. We include it in the analysis just to show that it has large Cook’s D and demonstrate how it will be handled by proc robustreg. Now we will look at the residuals. We will generate a new variable called absr1, which is the absolute value of the residuals (because the sign of the residual doesn’t matter). We then print the ten observations with the highest absolute residual values.
data t2; set t; rabs = abs(res); run; proc sort data = t2; by descending rabs; run; proc print data = t2 (obs=10); run;p p r c c p e m t t o s s s c u m w p v i c i t r r e h c e n o d r O s a i d t i t r g r o l _ a b i t m e r t h t l e k e s b s d e e r o e s y e s d v q s 1 25 ms 434 13.5 30.7 63.3 64.3 24.7 14.7 -3.56299 0.61387 0.12669 12.6949 3.56299 2 9 fl 1206 8.9 93.0 83.5 74.4 17.8 10.6 2.90266 0.14259 0.04832 8.4255 2.90266 3 51 dc 2922 78.5 100.0 31.8 73.1 26.4 22.1 2.61645 2.63625 0.53602 6.8458 2.61645 4 46 vt 114 3.6 27.0 98.4 80.8 10.0 11.0 -1.74241 0.04272 0.04050 3.0360 1.74241 5 26 mt 178 3.0 24.0 92.6 81.0 14.9 10.8 -1.46088 0.01676 0.02301 2.1342 1.46088 6 21 me 126 1.6 35.7 98.5 78.8 10.7 10.6 -1.42674 0.02233 0.03186 2.0356 1.42674 7 1 ak 761 9.0 41.8 75.2 86.6 9.1 14.3 -1.39742 0.12547 0.16161 1.9528 1.39742 8 31 nj 627 5.3 100.0 80.8 76.7 10.9 9.6 1.35415 0.02229 0.03519 1.8337 1.35415 9 14 il 960 11.4 84.0 81.0 76.2 13.6 11.5 1.33819 0.01266 0.02076 1.7908 1.33819 10 20 md 998 12.7 92.8 68.9 78.4 9.7 12.0 1.28709 0.03570 0.06072 1.6566 1.28709
Now let’s run our first robust regression. Robust regression is done by iterated re-weighted least squares. The procedure for running robust regression is proc robustreg. There are a couple of estimators for IWLS. We are going to first use the Huber weights in this example. We can save the final weights created by the IWLS process. This can be very useful. We will use the data set t2 generated above.
proc robustreg data=t2 method=m (wf=huber) ; model crime = poverty single; output out = t3 weight=wgt; run; Model Information Data Set WORK.T2 Dependent Variable crime Number of Independent Variables 2 Number of Observations 51 Method M Estimation Number of Observations Read 51 Number of Observations Used 51 Summary Statistics Standard Variable Q1 Median Q3 Mean Deviation MAD poverty 10.7000 13.1000 17.4000 14.2588 4.5842 4.2995 single 10.0000 10.9000 12.1000 11.3255 2.1215 1.4826 crime 326.0 515.0 780.0 612.8 441.1 345.4 Parameter Estimates Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1423.23 167.5099 -1751.54 -1094.91 72.19 <.0001 poverty 1 8.8694 8.0429 -6.8944 24.6331 1.22 0.2701 single 1 169.0012 17.3795 134.9381 203.0644 94.56 <.0001 Scale 1 181.7251 Diagnostics Summary Observation Type Proportion Cutoff Outlier 0.0392 3.0000 Goodness-of-Fit Statistic Value R-Square 0.5257 AICR 73.1089 BICR 78.9100 Deviance 2216391proc sort data = t3; by wgt ; run; proc print data = t3 (obs=15); var state crime poverty single res cookd lev wgt; run;Obs state crime poverty single res cookd lev wgt 1 ms 434 24.7 14.7 -3.56299 0.61387 0.12669 0.28886 2 fl 1206 17.8 10.6 2.90266 0.14259 0.04832 0.35947 3 vt 114 10.0 11.0 -1.74241 0.04272 0.04050 0.59545 4 dc 2922 26.4 22.1 2.61645 2.63625 0.53602 0.64980 5 mt 178 14.9 10.8 -1.46088 0.01676 0.02301 0.68630 6 me 126 10.7 10.6 -1.42674 0.02233 0.03186 0.72509 7 nj 627 10.9 9.6 1.35415 0.02229 0.03519 0.73812 8 il 960 13.6 11.5 1.33819 0.01266 0.02076 0.76600 9 ak 761 9.1 14.3 -1.39742 0.12547 0.16161 0.78039 10 md 998 9.7 12.0 1.28709 0.03570 0.06072 0.79570 11 ma 805 10.7 10.9 1.19854 0.01640 0.03311 0.83933 12 la 1062 26.4 14.9 -1.02183 0.06700 0.16143 0.91528 13 ca 1078 18.2 12.5 1.01521 0.01231 0.03458 1.00000 14 wy 286 13.3 10.8 -0.96626 0.00667 0.02099 1.00000 15 sc 1023 18.7 12.3 0.91213 0.01111 0.03853 1.00000
We can see that roughly, as the absolute residual goes down, the weight goes up. In other words, cases with a large residuals tend to be down-weighted. We can also see that the values of Cook's D don't really correspond to the weights. This output shows us that the observation for Mississippi will be down-weighted the most. Florida will also be substantially down-weighted. All observations not shown above have a weight of 1. In OLS regression, all cases have a weight of 1. Hence, the more cases in the robust regression that have a weight close to one, the closer the results of the OLS and robust regressions.
Next, let's run the same model, but using the default weighting function. Again, we can look at the weights.
proc robustreg data=t2 method=m (wf=bisquare);
model crime = poverty single;
output out = t4 weight=wgt;
run;
Model Information
Data Set WORK.T2
Dependent Variable crime
Number of Independent Variables 2
Number of Observations 51
Method M Estimation
Number of Observations Read 51
Number of Observations Used 51
Summary Statistics
Standard
Variable Q1 Median Q3 Mean Deviation MAD
poverty 10.7000 13.1000 17.4000 14.2588 4.5842 4.2995
single 10.0000 10.9000 12.1000 11.3255 2.1215 1.4826
crime 326.0 515.0 780.0 612.8 441.1 345.4
Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -1535.36 164.4627 -1857.70 -1213.02 87.15 <.0001
poverty 1 11.6911 7.8966 -3.7859 27.1681 2.19 0.1387
single 1 175.9320 17.0633 142.4884 209.3755 106.31 <.0001
Scale 1 202.3464
Diagnostics Summary
Observation
Type Proportion Cutoff
Outlier 0.0392 3.0000
Goodness-of-Fit
Statistic Value
R-Square 0.4545
AICR 55.1327
BICR 62.3771
Deviance 2071016
proc print data = t4 (obs=15);
var state crime poverty single res cookd lev wgt;
run;
Obs state crime poverty single res cookd lev wgt
1 ms 434 24.7 14.7 -3.56299 0.61387 0.12669 0.00764
2 fl 1206 17.8 10.6 2.90266 0.14259 0.04832 0.25292
3 vt 114 10.0 11.0 -1.74241 0.04272 0.04050 0.67151
4 mt 178 14.9 10.8 -1.46088 0.01676 0.02301 0.73114
5 nj 627 10.9 9.6 1.35415 0.02229 0.03519 0.75135
6 la 1062 26.4 14.9 -1.02183 0.06700 0.16143 0.76887
7 me 126 10.7 10.6 -1.42674 0.02233 0.03186 0.77412
8 ak 761 9.1 14.3 -1.39742 0.12547 0.16161 0.77766
9 il 960 13.6 11.5 1.33819 0.01266 0.02076 0.79368
10 md 998 9.7 12.0 1.28709 0.03570 0.06072 0.79908
11 ma 805 10.7 10.9 1.19854 0.01640 0.03311 0.81260
12 dc 2922 26.4 22.1 2.61645 2.63625 0.53602 0.85455
13 wy 286 13.3 10.8 -0.96626 0.00667 0.02099 0.88166
14 ca 1078 18.2 12.5 1.01521 0.01231 0.03458 0.91174
15 ga 723 13.5 13.0 -0.68492 0.00691 0.04232 0.92402
We can see that the weight given to Mississippi is dramatically lower using the bisquare weighting function than the Huber weighting function and the parameter estimates from these two different weighting methods differ. When comparing the results of a regular OLS regression and a robust regression, if the results are very different, you will most likely want to use the results from the robust regression. Large differences suggest that the model parameters are being highly influenced by outliers. When using robust regression, SAS documentation notes: "estimates are more sensitive to the parameters of these weight functions than to the type of the weight function". However, different functions have advantages and drawbacks. Huber weights can have difficulties with severe outliers, and bisquare weights can have difficulties converging or may yield multiple solutions.
As you can see, the results from the two analyses are fairly different,
especially with respect to the coefficients of single and the constant (_cons).
While normally we are not interested in the constant, if you had centered one or
both of the predictor variables, the constant would be useful. On the
other hand, you will notice that poverty is not statistically significant
in either analysis, while single is significant in both analyses.
Things to consider
- Proc robustreg does not address issues of heterogeneity of variance. This problem can be addressed by using proc surveyreg. Details can be found in this SAS Code Fragment.
- The examples shown here have presented SAS code for M estimation. There are other estimation options available in proc robustreg: Least trimmed squares, S estimation, and MM estimation. See the SAS documentation for when and how these alternatives are preferable.
References
- Li, G. 1985. Robust regression. In Exploring Data Tables, Trends, and Shapes, ed. D. C. Hoaglin, F. Mosteller, and J. W. Tukey, Wiley.
- Chen, C. 2002. Robust Regression and Outlier Detection with the ROBUSTREG Procedure. Proceedings of the 27th SAS Users Group International Conference, Cary NC: SAS Institute, Inc.
- John Fox, Applied regression analysis, linear models, and related models, Sage publications, Inc, 1997
See also