Poisson regression is for modeling count variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
This example was done using SAS version 9.22.
Examples of Poisson regression
Example 1. The number of persons killed by mule or horse kicks in the Prussian army per year. von Bortkiewicz collected data from 20 volumes of Preussischen Statistik. These data were collected on 10 corps of the Prussian army in the late 1800s over the course of 20 years.
Example 2. A health-related researcher is studying the number of hospital visits in past 12 months by senior citizens in a community based on the characteristics of the individuals and the types of health plans under which each one is covered.
Example 3. A researcher in education is interested in the association between the number of awards earned by students at one high school and the students’ performance in math and the type of program (e.g., vocational, general or academic) in which students were enrolled.
Description of the data
For the purpose of illustration, we have simulated a data set for Example 3 above: https://stats.idre.ucla.edu/wp-content/uploads/2016/02/poisson_sim.sas7bdat. In this example, num_awards is the outcome variable and indicates the number of awards earned by students at a high school in a year, math is a continuous predictor variable and represents students’ scores on their math final exam, and prog is a categorical predictor variable with three levels indicating the type of program in which the students were enrolled. It is coded as 1 = “General”, 2 = “Academic” and 3 = “Vocational”.
proc means data = poisson_sim n mean var min max; var num_awards math; run; The MEANS Procedure Variable Label N Mean Variance Minimum Maximum ----------------------------------------------------------------------------------------------- num_awards 200 0.6300000 1.1086432 0 6.0000000 math math score 200 52.6450000 87.7678141 33.0000000 75.0000000 -----------------------------------------------------------------------------------------------
Each variable has 200 valid observations and their distributions seem quite reasonable. The unconditional mean and variance of our outcome variable are not extremely different. Our model assumes that these values, conditioned on the predictor variables, will be equal (or at least roughly so).
We can look at summary statistics by program type. The table below shows the mean and variance of numbers of awards by program type and seems to suggest that program type is a good candidate for predicting the number of awards, our outcome variable, because the mean value of the outcome appears to vary by prog. Additionally, the means and variances within each level of prog–the conditional means and variances–are similar. A frequency plot is also produced to display the distribution of the outcome variable.
proc means data = poisson_sim mean var; class prog; var num_awards; run; The MEANS Procedure Analysis Variable : num_awards type of N program Obs Mean Variance --------------------------------------------------- 1 45 0.2000000 0.1636364 2 105 1.0000000 1.6346154 3 50 0.2400000 0.2677551 --------------------------------------------------- proc freq data=poisson_sim; tables num_awards / plots=freqplot; run;proc freq data = poisson_sim; tables prog; run;
The FREQ Procedure type of program Cumulative Cumulative prog Frequency Percent Frequency Percent --------------------------------------------------------- 1 45 22.50 45 22.50 2 105 52.50 150 75.00 3 50 25.00 200 100.00
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Poisson regression – Poisson regression is often used for modeling count data. It has a number of extensions useful for count models.
- Negative binomial regression – Negative binomial regression can be used for over-dispersed count data, that is when the conditional variance exceeds the conditional mean. It can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression and it has an extra parameter to model the over-dispersion. If the conditional distribution of the outcome variable is over-dispersed, the confidence intervals for Negative binomial regression are likely to be narrower as compared to those from a Poisson regession.
- Zero-inflated regression model – Zero-inflated models attempt to account for excess zeros. In other words, two kinds of zeros are thought to exist in the data, “true zeros” and “excess zeros”. Zero-inflated models estimate two equations simultaneously, one for the count model and one for the excess zeros.
- OLS regression – Count outcome variables are sometimes log-transformed and analyzed using OLS regression. Many issues arise with this approach, including loss of data due to undefined values generated by taking the log of zero (which is undefined) and biased estimates.
Poisson regression analysis
At this point, we are ready to perform our Poisson model analysis. Proc genmod is usually used for Poisson regression analysis in SAS.
On the class statement we list the variable prog, since prog is a categorical variable. We use the global option param = glm so we can save the model using the store statement for future post estimations. The type3 option in the model statement is used to get the multi-degree-of-freedom test of the categorical variables listed on the class statement, and the dist = poisson option is used to indicate that a Poisson distribution should be used. Statement “store” allows us to store the parameter estimates to a data set, which we call p1, so we can perform post estimation without rerunning the model.
proc genmod data = poisson_sim;
class prog /param=glm;
model num_awards = prog math / type3 dist=poisson;
store p1;
run;
The GENMOD Procedure
Model Information
Data Set WORK.POISSON_SIM
Distribution Poisson
Link Function Log
Dependent Variable num_awards
Number of Observations Read 200
Number of Observations Used 200
Class Level Information
Class Levels Values
prog 3 1 2 3
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 196 189.4496 0.9666
Scaled Deviance 196 189.4496 0.9666
Pearson Chi-Square 196 212.1437 1.0824
Scaled Pearson X2 196 212.1437 1.0824
Log Likelihood -135.1052
Full Log Likelihood -182.7523
AIC (smaller is better) 373.5045
AICC (smaller is better) 373.7096
BIC (smaller is better) 386.6978
Algorithm converged.
Analysis Of Maximum Likelihood Parameter Estimates
Standard Wald 95% Confidence Wald
Parameter DF Estimate Error Limits Chi-Square Pr > ChiSq
Intercept 1 -4.8773 0.6282 -6.1085 -3.6461 60.28 <.0001
prog 1 1 -0.3698 0.4411 -1.2343 0.4947 0.70 0.4018
prog 2 1 0.7140 0.3200 0.0868 1.3413 4.98 0.0257
prog 3 0 0.0000 0.0000 0.0000 0.0000 . .
math 1 0.0702 0.0106 0.0494 0.0909 43.81 <.0001 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed. LR Statistics For Type 3 Analysis Chi- Source DF Square Pr > ChiSq
prog 2 14.57 0.0007
math 1 45.01 <.0001
- The output begins with the basic model information and then provides a list of goodness-of-fit statistics including the log likelihood, AIC, and BIC.
- Next you will find the Poisson regression coefficients for each of the variables along with standard errors, Wald Chi-Square statistics and intervals, and p-values for the coefficients. The coefficient for math is .07. This means that the expected increase in log count for a one-unit increase in math is .07. For our three-level categorical predictor prog, the model presents coefficients relating levels 1 and 2 to level 3. The indicator variable prog(2) is the expected difference in log count between group 2 (prog=2) and the reference group (prog=3). So the expected log count for level 2 of prog is 0.714 higher than the expected log count for level 3 of prog. Similarly the expected log count for level 1 of prog is 0.3698 lower than the expected log count for level 3.
- To determine if prog itself, overall, is statistically significant, we can look at the Type 3 table in the outcome that includes the two degrees-of-freedom test of this variable. This is testing the null hypothesis that both prog estimates (level 1 vs. level 3 and level 2 vs. level 3) are equal to zero. We see there that prog is a statistically significant predictor.
To help assess the fit of the model, we can use the goodness-of-fit chi-squared test. This assumes the deviance follows a chi-square distribution with degrees of freedom equal to the model residual. From the first line of our Goodness of Fit output, we can see these values are 189.4495 and 196.
data pvalue; df = 196; chisq = 189.4495; pvalue = 1 - probchi(chisq, df); run; proc print data = pvalue noobs; run; df chisq pvalue 196 189.450 0.61823
This is not a test of the model coefficients (which we saw in the header information), but a test of the model form: Does the poisson model form fit our data? We conclude that the model fits reasonably well because the goodness-of-fit chi-squared test is not statistically significant. If the test had been statistically significant, it would indicate that the data do not fit the model well. In that situation, we may try to determine if there are omitted predictor variables, if our linearity assumption holds and/or if there is an issue of over-dispersion.
Cameron and Trivedi (2009) recommend using robust standard errors for the parameter estimates to control for mild violation of the distribution assumption that the variance equals the mean. In SAS, we can do this by running proc genmod with the repeated statement in order to obtain robust standard errors for the Poisson regression coefficients.
proc genmod data = poisson_sim;
class prog id /param=glm;
model num_awards = prog math /dist=poisson;
repeated subject=id;
run;
GEE Model Information
Correlation Structure Independent
Subject Effect id (200 levels)
Number of Clusters 200
Correlation Matrix Dimension 1
Maximum Cluster Size 1
Minimum Cluster Size 1
Algorithm converged.
GEE Fit Criteria
QIC 256.8581
QICu 257.6478
Analysis Of GEE Parameter Estimates
Empirical Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept -4.8773 0.6297 -6.1116 -3.6430 -7.74 <.0001
prog 1 -0.3698 0.4004 -1.1546 0.4150 -0.92 0.3557
prog 2 0.7140 0.2986 0.1287 1.2994 2.39 0.0168
prog 3 0.0000 0.0000 0.0000 0.0000 . .
math 0.0702 0.0104 0.0497 0.0906 6.72 <.0001
We can see that our estimates are unchanged, but our standard errors are slightly different.
We have the model stored in a data set called p1. Using proc plm, we can request many different post estimation tasks. For example, we might want to displayed the results as incident rate ratios (IRR). We can do so with a data step after using proc plm to create a dataset of our model estimates.
ods output ParameterEstimates = est; proc plm source = p1; show parameters; run; data est_exp; set est; irr = exp(estimate); if parameter ^="Intercept"; run; proc print data = est_exp; run;Obs Parameter prog Estimate StdErr irr 1 type of program 1 1 -0.3698 0.4411 0.69087 2 type of program 2 2 0.7140 0.3200 2.04225 3 type of program 3 3 0 . 1.00000 4 math score _ 0.07015 0.01060 1.07267
The output above indicates that the incident rate for prog=2 is 2.04 times the incident rate for the reference group (prog=3). Likewise, the incident rate for prog=1 is 0.69 times the incident rate for the reference group holding the other variables constant. The percent change in the incident rate of num_awards is 100 × (1.07267 – 1) % ≈ 7 % for every unit increase in math, holding other variables constant.
Recall the form of our model equation:
log(num_awards) = Intercept + b1(prog=1) + b2(prog=2) + b3math.
This implies:
num_awards = exp(Intercept + b1(prog=1) + b2(prog=2)+ b3math) = exp(Intercept) * exp(b1(prog=1)) * exp(b2(prog=2)) * exp(b3math)
The coefficients have an additive effect in the log(y) scale and the IRR have a multiplicative effect in the y scale.
For additional information on the various metrics in which the results can be presented, and the interpretation of such, please see Regression Models for Categorical Dependent Variables Using Stata, Second Edition by J. Scott Long and Jeremy Freese (2006).
Below we use lsmeans statements in proc plm to calculate the predicted number of events at each level of prog, holding all other variables (in this example, math) in the model at their means.
We use the “ilink” option (for inverse link) to get the predicted means (predicted count) in addition to the linear predictions.
proc plm source = p1; lsmeans prog /ilink cl; run;
prog Least Squares Means type of Standard program Estimate Error z Value Pr > |z| Alpha Lower Upper 1 -1.5540 0.3335 -4.66 <.0001 0.05 -2.2076 -0.9003 2 -0.4701 0.1381 -3.40 0.0007 0.05 -0.7407 -0.1995 3 -1.1841 0.2887 -4.10 <.0001 0.05 -1.7499 -0.6183 prog Least Squares Means Standard type of Error of Lower Upper program Mean Mean Mean Mean 1 0.2114 0.07050 0.1100 0.4064 2 0.6249 0.08628 0.4768 0.8191 3 0.3060 0.08834 0.1738 0.5388
The first block of output above shows the predicted log count. The second block shows predicted number of events in the “mean” column.
In the output above, we see that the predicted number of events for level 1 of prog is about .21, holding math at its mean. The predicted number of events for level 2 of prog is higher at .62, and the predicted number of events for level 3 of prog is about .31. Note that the predicted count of level 1 of prog is (.2114/.3060) = 0.6908 times the predicted count for level 3 of prog. This matches what we saw in the IRR output table.
Below we will obtain the averaged predicted counts for values of math that range from 35 to 75 in increments of 10, using a data step and the score statement of proc plm.
data toscore; set poisson_sim; do math_cat = 35 to 75 by 10; math = math_cat; output; end; run; proc plm source=p1; score data = toscore out=math /ilink; run; proc means data = math mean; class math_cat; var predicted; run;N math_cat Obs Mean ------------------------------------ 35 200 0.131132645 200 0.264471455 200 0.533392365 200 1.075758475 200 2.1696153
The table above shows that with prog at its observed values and math held at 35 for all observations, the average predicted count (or average number of awards) is about .13; when math = 75, the average predicted count is about 2.17.
If we compare the predicted counts at math = 35 and math = 45, we can see that the ratio is (.2644714/.1311326) = 2.017. This matches the IRR of 1.0727 for a 10 unit change: 1.0727^10 = 2.017.
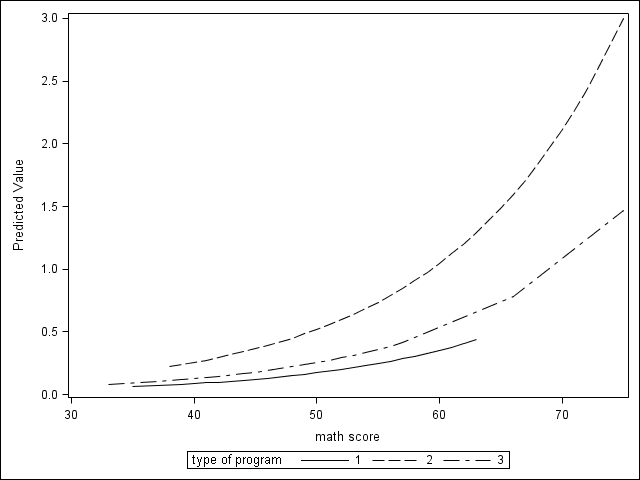
You can graph the predicted number of events using proc plm and proc sgplot below.
ods graphics on; ods html style=journal; proc plm source=p1; score data = poisson_sim out=pred /ilink; run; proc sort data = pred; by prog math; run; proc sgplot data = pred; series x = math y = predicted /group=prog; run; ods graphics off;
Things to consider
- When there seems to be an issue of dispersion, we should first check if our model is appropriately specified, such as omitted variables and functional forms. For example, if we omitted the predictor variable prog in the example above, our model would seem to have a problem with over-dispersion. In other words, a mis-specified model could present a symptom like an over-dispersion problem.
- Assuming that the model is correctly specified, you may want to check for overdispersion. There are several tests including the likelihood ratio test of over-dispersion parameter alpha by running the same regression model using negative binomial distribution.
- One common cause of over-dispersion is excess zeros, which in turn are generated by an additional data generating process. In this situation, a zero-inflated model should be considered.
- If the data-generating process does not allow for any 0s (such as the number of days spent in the hospital), then a zero-truncated model may be more appropriate.
- The outcome variable in a Poisson regression cannot have negative numbers.
- Poisson regression is estimated via maximum likelihood estimation. It usually requires a large sample size.
References
- Cameron, A. C. and Trivedi, P. K. 2009. Microeconometrics Using Stata. College Station, TX: Stata Press.
- Cameron, A. C. and Trivedi, P. K. 1998. Regression Analysis of Count Data. New York: Cambridge Press.
- Cameron, A. C. Advances in Count Data Regression Talk for the Applied Statistics Workshop, March 28, 2009. http://cameron.econ.ucdavis.edu/racd/count.html .
- Dupont, W. D. 2002. Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data. New York: Cambridge Press.
- Long, J. S. 1997. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
- Long, J. S. and Freese, J. 2006. Regression Models for Categorical Dependent Variables Using Stata, Second Edition. College Station, TX: Stata Press.
See also
- Annotated output for the poisson command
- SAS Online Manual