Version info: Code for this page was tested in SAS 9.3.
Linear discriminant function analysis (i.e., discriminant analysis) performs a multivariate test of differences between groups. In addition, discriminant analysis is used to determine the minimum number of dimensions needed to describe these differences. A distinction is sometimes made between descriptive discriminant analysis and predictive discriminant analysis. We will be illustrating predictive discriminant analysis on this page.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of discriminant function analysis
Example 1. A large international air carrier has collected data on employees in three different job classifications; 1) customer service personnel, 2) mechanics and 3) dispatchers. The director of Human Resources wants to know if these three job classifications appeal to different personality types. Each employee is administered a battery of psychological test which include measures of interest in outdoor activity, sociability and conservativeness.
Example 2. There is Fisher’s (1936) classic example of discriminant analysis involving three varieties of iris and four predictor variables (petal width, petal length, sepal width, and sepal length). Fisher not only wanted to determine if the varieties differed significantly on the four continuous variables but he was also interested in predicting variety classification for unknown individual plants.
Description of the data
Let’s pursue Example 1 from above.
We have a data file, discrim.sas7bdat, with 244 observations on four variables. The psychological variables are outdoor interests, social and conservative. The categorical variable is job type with three levels; 1) customer service, 2) mechanic, and 3) dispatcher.
Let’s look at the data.
proc means data=mylib.discrim n mean std min max;
var outdoor social conservative;
run;
The MEANS Procedure
Variable N Mean Std Dev Minimum Maximum
-----------------------------------------------------------------------------------
OUTDOOR 244 15.6393443 4.8399326 0 28.0000000
SOCIAL 244 20.6762295 5.4792621 7.0000000 35.0000000
CONSERVATIVE 244 10.5901639 3.7267890 0 20.0000000
-----------------------------------------------------------------------------------
proc means data=mylib.discrim n mean std;
class job;
var outdoor social conservative;
run;
The MEANS Procedure
N
JOB Obs Variable N Mean Std Dev
--------------------------------------------------------------------------
1 85 OUTDOOR 85 12.5176471 4.6486346
SOCIAL 85 24.2235294 4.3352829
CONSERVATIVE 85 9.0235294 3.1433091
2 93 OUTDOOR 93 18.5376344 3.5648012
SOCIAL 93 21.1397849 4.5506602
CONSERVATIVE 93 10.1397849 3.2423535
3 66 OUTDOOR 66 15.5757576 4.1102521
SOCIAL 66 15.4545455 3.7669895
CONSERVATIVE 66 13.2424242 3.6922397
--------------------------------------------------------------------------
proc corr data=mylib.discrim;
var outdoor social conservative;
run;
<**SOME OUTPUT OMITTED**>
Pearson Correlation Coefficients, N = 244
Prob > |r| under H0: Rho=0
OUTDOOR SOCIAL CONSERVATIVE
OUTDOOR 1.00000 -0.07130 0.07938
0.2672 0.2166
SOCIAL -0.07130 1.00000 -0.23586
0.2672 0.0002
CONSERVATIVE 0.07938 -0.23586 1.00000
0.2166 0.0002
proc freq data=mylib.discrim;
tables job;
run;
The FREQ Procedure
Cumulative Cumulative
JOB Frequency Percent Frequency Percent
--------------------------------------------------------
1 85 34.84 85 34.84
2 93 38.11 178 72.95
3 66 27.05 244 100.00
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Discriminant function analysis – The focus of this page. This procedure is multivariate and also provides information on the individual dimensions.
- Multinomial logistic regression or multinomial probit – These are also viable options.
- MANOVA – The tests of significance are the same as for discriminant function analysis, but MANOVA gives no information on the individual dimensions. However, the psychological variables will be the dependent variables and job type the independent variable.
- Separate one-way ANOVAs – You could analyze these data using separate one-way ANOVAs for each psychological variable. The separate ANOVAs will not produce multivariate results and do not report information concerning dimensionality. Again, the designation of independent and dependent variables is reversed as in MANOVA.
Discriminant function analysis
We will run the discriminant analysis using proc discrim with the canonical option in the proc discrim statement to output the canonical coefficients and canonical structure. We could also have used proc candisc with essentially the same syntax to obtain the same results but with slightly different output. Please note that we will not be using all of the output that SAS provides nor will the output be presented in the same order as it appears. There is still a lot of output remaining so we will comment at various places along the way.
proc candisc data=mylib.discrim out=discrim_out ;
class job;
var outdoor social conservative;
run;
The DISCRIM Procedure
Canonical Discriminant Analysis
Adjusted Approximate Squared
Canonical Canonical Standard Canonical
Correlation Correlation Error Correlation
1 0.720661 0.716099 0.030834 0.519353
2 0.492659 . 0.048580 0.242713
Test of H0: The canonical correlations in
Eigenvalues of Inv(E)*H the current row and all that follow are zero
= CanRsq/(1-CanRsq)
Likelihood Approximate
Eigenvalue Difference Proportion Cumulative Ratio F Value Num DF Den DF Pr > F
1 1.0805 0.7600 0.7712 0.7712 0.36398797 52.38 6 478 <.0001
2 0.3205 0.2288 1.0000 0.75728681 38.46 2 240 <.0001
There are two discriminant dimensions both of which are statistically significant. The canonical correlations for the dimensions one and two are 0.72 and 0.49 respectively.
Pooled Within-Class Standardized Canonical Coefficients
Variable Can1 Can2
OUTDOOR -.3785725108 0.9261103825
SOCIAL 0.8306986150 0.2128592590
CONSERVATIVE -.5171682475 -.2914406390
Pooled Within Canonical Structure
Variable Can1 Can2
OUTDOOR -0.323098 0.937215
SOCIAL 0.765391 0.266030
CONSERVATIVE -0.467691 -0.258743
The standardized discriminant coefficients function in a manner analogous to standardized regression coefficients in OLS regression. For example, a one standard deviation increase on the outdoor variable will result in a .378 standard deviation decrease in the predicted values on discriminant function 1. The canonical structure, also known as canonical loading or discriminant loadings, represent correlations between observed variables and the unobserved discriminant functions (dimensions). The discriminant functions are a kind of latent variable and the correlations are loadings analogous to factor loadings.
Class Means on Canonical Variables
JOB Can1 Can2
1 1.219100186 -0.389003864
2 -0.106724637 0.714570441
3 -1.419668555 -0.505904888
Number of Observations and Percent Classified into JOB
From JOB 1 2 3 Total
1 70 11 4 85
82.35 12.94 4.71 100.00
2 16 62 15 93
17.20 66.67 16.13 100.00
3 3 12 51 66
4.55 18.18 77.27 100.00
Total 89 85 70 244
36.48 34.84 28.69 100.00
Priors 0.33333 0.33333 0.33333
The output includes the means on the discriminant functions for each of the three groups and a classification table. Values in the diagonal of the classification table reflect the correct classification of individuals into groups based on their scores on the discriminant dimensions.
Next, we will plot a graph of individuals on the discriminant dimensions. Specifically, we are going to overlay a scatter plot of the individuals’ scores on each dimension on top of a contour plot indicating predicted job classification as a function of the two discriminant dimensions. To create the contour plot, we first create a fake dataset containing a range of plausible values. Then we will use these fake data as a test dataset to calculate predicted job classifications using coefficient estimates derived from the real dataset. The predicted job classifications are saved in the output dataset under the variable name _into_. We will then merge the actual job classifications of the real data with the predicted job classifications of the fake data into a single dataset for plotting. Finally we will use proc sgrender to plot the scatter plot and contour plot in one graph. To use proc sgrender, we first need to define a graph template with proc template, in which we provide all of our graphing specifications. Here, we are requesting a contour plot, where x and y are the discriminant dimensions and the coloring indicates job classification, as well as a scatter plot, where x and y are the two discriminant dimensions and the job classification of each data point is indicated by a number (1,2,3).
data fakedata;
do outdoor = 0 to 30 by 1;
do social = 5 to 40 by 1;
do conservative = 0 to 25 by 1;
output;
end;
end;
end;
run;
proc discrim data=mylib.discrim testdata=fakedata testout=fake_out out=discrim_out canonical;
class job;
var outdoor social conservative;
run;
data plotclass;
merge fake_out discrim_out;
run;
proc template;
define statgraph classify;
begingraph;
layout overlay;
contourplotparm x=Can1 y=Can2 z=_into_ / contourtype=fill
nhint = 30 gridded = false;
scatterplot x=Can1 y=Can2 / group=job includemissinggroup=false
markercharactergroup = job;
endlayout;
endgraph;
end;
run;
proc sgrender data = plotclass template = classify;
run;
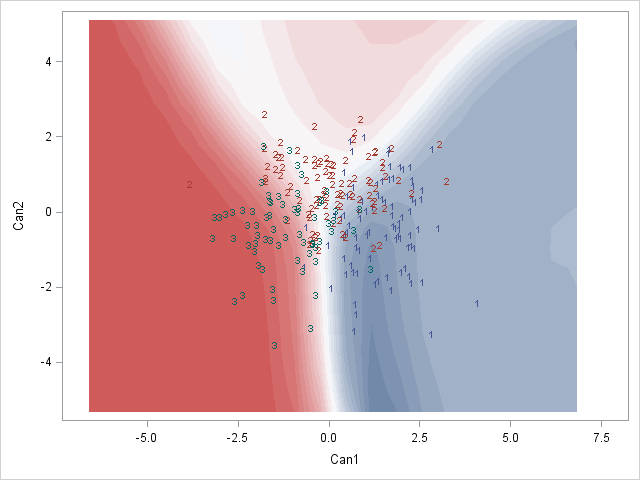
Here we see that the two discriminant dimensions do a reasonable job of separating the job classifications: most of the actual job classifications fall within the boundaries of the matching predicted job classification, indicated by the coloring of the underlying contour map. Moreover, it seems job levels 1 and 3 are rather different, while job level 2 is less separable from the other two.
Things to consider
- Multivariate normal distribution assumptions holds for the response variables. This means that each of the dependent variables is normally distributed within groups, that any linear combination of the dependent variables is normally distributed, and that all subsets of the variables must be multivariate normal.
- Each group must have a sufficiently large number of cases.
- Different classification methods may be used depending on whether the variance-covariance matrices are equal (or very similar) across groups.
- Non-parametric discriminant function analysis, called kth nearest neighbor, can also be performed.
See Also
- SAS Online Manual
References
- Afifi, A, Clark, V and May, S. 2004. Computer-Aided Multivariate Analysis. 4th ed. Boca Raton, Fl: Chapman & Hall/CRC.
- Grimm, L. G. and Yarnold, P. R. (editors). (1995). Reading and Understanding Multivariate Statistics. Washington, D.C.: American Psychological Association.
- Huberty, C. J. and Olejnik, S. (2006). Applied MANOVA and Discriminant Analysis, Second Edition. Hoboken, New Jersey: John Wiley and Sons, Inc.
- Stevens, J. P. (2002). Applied Multivariate Statistics for the Social Sciences, Fourth Edition. Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc.
- Tatsuoka, M. M. (1971). Multivariate Analysis: Techniques for Educational and Psychological Research. New York: John Wiley and Sons.
