Zero-inflated Poisson regression is used to model count data that has an excess of zero counts. Further, theory suggests that the excess zeros are generated by a separate process from the count values and that the excess zeros can be modeled independently. Thus, the zip model has two parts, a Poisson count model and the logit model for predicting excess zeros. You may want to review these Data Analysis Example pages, Poisson Regression and Logit Regression.
This page uses the following packages. Make sure that you can load
them before trying to run the examples on this page. If you do not have
a package installed, run: install.packages("packagename"), or
if you see the version is out of date, run: update.packages().
require(ggplot2) require(pscl) require(boot)
Version info: Code for this page was tested in R version 3.4.1
Please Note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and verification, verification of assumptions, model diagnostics and potential follow-up analyses.
Examples of Zero-Inflated Poisson regression
Example 1. School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include gender of the student and standardized test scores in math and language arts.
Example 2. The state wildlife biologists want to model how many fish are being caught by fishermen at a state park. Visitors are asked how long they stayed, how many people were in the group, were there children in the group and how many fish were caught. Some visitors do not fish, but there is no data on whether a person fished or not. Some visitors who did fish did not catch any fish so there are excess zeros in the data because of the people that did not fish.
Description of the data
Let’s pursue Example 2 from above.
We have data on 250 groups that went to a park. Each group was questioned
about how many fish they caught (count), how many children were in the
group (child), how many people were in the group (persons), and
whether or not they brought a camper to the park (camper).
In addition to predicting the number of fish caught, there is interest in
predicting the existence of excess zeros, i.e., the probability that a group
caught zero fish. We will use the variables child, persons, and
camper in our model. Let’s look at the data.
zinb <- read.csv("https://stats.idre.ucla.edu/stat/data/fish.csv") zinb <- within(zinb, { nofish <- factor(nofish) livebait <- factor(livebait) camper <- factor(camper) }) summary(zinb)
## nofish livebait camper persons child xb ## 0:176 0: 34 0:103 Min. :1.00 Min. :0.000 Min. :-3.275 ## 1: 74 1:216 1:147 1st Qu.:2.00 1st Qu.:0.000 1st Qu.: 0.008 ## Median :2.00 Median :0.000 Median : 0.955 ## Mean :2.53 Mean :0.684 Mean : 0.974 ## 3rd Qu.:4.00 3rd Qu.:1.000 3rd Qu.: 1.964 ## Max. :4.00 Max. :3.000 Max. : 5.353 ## zg count ## Min. :-5.626 Min. : 0.0 ## 1st Qu.:-1.253 1st Qu.: 0.0 ## Median : 0.605 Median : 0.0 ## Mean : 0.252 Mean : 3.3 ## 3rd Qu.: 1.993 3rd Qu.: 2.0 ## Max. : 4.263 Max. :149.0
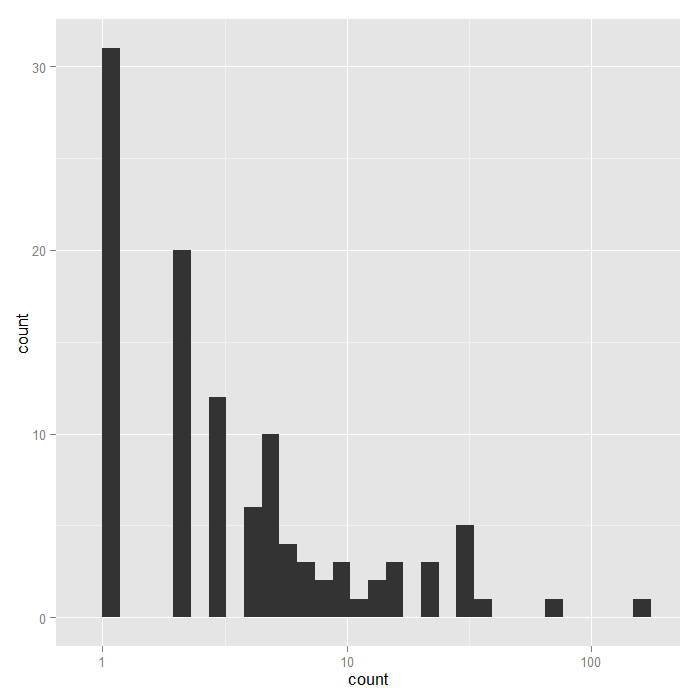
## histogram with x axis in log10 scale ggplot(zinb, aes(count)) + geom_histogram() + scale_x_log10()
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable while others have either fallen out of favor or have limitations.
- Zero-inflated Poisson Regression – The focus of this web page.
- Zero-inflated Negative Binomial Regression – Negative binomial regression does better with over dispersed data, i.e. variance much larger than the mean.
- Ordinary Count Models – Poisson or negative binomial models might be more appropriate if there are no excess zeros.
- OLS Regression – You could try to analyze these data using OLS regression. However, count data are highly non-normal and are not well estimated by OLS regression.
Zero-inflated Poisson regression
Though we can run a Poisson regression in R using the glm function in
one of the core packages, we need another package to run
the zero-inflated Poisson model. We use the pscl package.
summary(m1 <- zeroinfl(count ~ child + camper | persons, data = zinb))
## Call: ## zeroinfl(formula = count ~ child + camper | persons, data = zinb) ## ## Pearson residuals: ## Min 1Q Median 3Q Max ## -1.2369 -0.7540 -0.6080 -0.1921 24.0847 ## ## Count model coefficients (poisson with log link): ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 1.59789 0.08554 18.680 <2e-16 *** ## child -1.04284 0.09999 -10.430 <2e-16 *** ## camper1 0.83402 0.09363 8.908 <2e-16 *** ## ## Zero-inflation model coefficients (binomial with logit link): ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 1.2974 0.3739 3.470 0.000520 *** ## persons -0.5643 0.1630 -3.463 0.000534 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Number of iterations in BFGS optimization: 12 ## Log-likelihood: -1032 on 5 Df
The output looks very much like the output from two OLS regressions in R. Below the model call, you will find a block of output containing Poisson regression coefficients for each of the variables along with standard errors, z-scores, and p-values for the coefficients. A second block follows that corresponds to the inflation model. This includes logit coefficients for predicting excess zeros along with their standard errors, z-scores, and p-values.
All of the predictors in both the count and inflation portions of the model are statistically significant. This model fits the data significantly better than the null model, i.e., the intercept-only model. To show that this is the case, we can compare with the current model to a null model without predictors using chi-squared test on the difference of log likelihoods.
mnull <- update(m1, . ~ 1) pchisq(2 * (logLik(m1) - logLik(mnull)), df = 3, lower.tail = FALSE)
## 'log Lik.' 4.041e-41 (df=5)
Since we have three predictor variables in the full model, the degrees of freedom for the chi-squared test is 3. This yields a high significant p-value; thus, our overall model is statistically significant.
We can get confidence intervals for the parameters and the
exponentiated parameters using bootstrapping. For the Poisson model, these would
be incident risk ratios, for the zero inflation model, odds ratios. We use the
boot package. First, we get the coefficients from our original model to
use as start values for the model to speed up the time it takes to estimate. Then
we write a short function that takes data and indices as input and returns the
parameters we are interested in. Finally, we pass that
to the boot function and do 1200 replicates, using snow to distribute across
four cores. Note that you should adjust the number of cores to whatever your machine
has. Also, for final results, one may wish to increase the number of replications to
help ensure stable results.
dput(coef(m1, "count"))
## structure(c(1.59788828690411, -1.04283909332231, 0.834023618148891
## ), .Names = c("(Intercept)", "child", "camper1"))
dput(coef(m1, "zero"))
## structure(c(1.29744027908309, -0.564347365357873), .Names = c("(Intercept)",
## "persons"))
f <- function(data, i) { require(pscl) m <- zeroinfl(count ~ child + camper | persons, data = data[i, ], start = list(count = c(1.598, -1.0428, 0.834), zero = c(1.297, -0.564))) as.vector(t(do.call(rbind, coef(summary(m)))[, 1:2])) } set.seed(10) res <- boot(zinb, f, R = 1200, parallel = "snow", ncpus = 4) ## print results res
## ## ORDINARY NONPARAMETRIC BOOTSTRAP ## ## ## Call: ## boot(data = zinb, statistic = f, R = 1200, parallel = "snow", ## ncpus = 4) ## ## ## Bootstrap Statistics : ## original bias std. error ## t1* 1.59789 -0.056661 0.30307 ## t2* 0.08554 0.004257 0.01670 ## t3* -1.04284 -0.002510 0.40557 ## t4* 0.09999 0.004395 0.01539 ## t5* 0.83402 0.017178 0.40465 ## t6* 0.09363 0.004581 0.01536 ## t7* 1.29744 0.020810 0.48058 ## t8* 0.37385 0.008224 0.03662 ## t9* -0.56435 -0.030103 0.26673 ## t10* 0.16296 0.005272 0.02981
The results are alternating parameter estimates and standard
errors. That is, the first row has the first parameter estimate
from our model. The second has the standard error for the
first parameter. The third column contains the bootstrapped
standard errors, which are considerably larger than those estimated
by zeroinfl.
Now we can get the confidence intervals for all the parameters. We start on the original scale with percentile and bias adjusted CIs. We also compare these results with the regular confidence intervals based on the standard errors.
## basic parameter estimates with percentile and bias adjusted CIs parms <- t(sapply(c(1, 3, 5, 7, 9), function(i) { out <- boot.ci(res, index = c(i, i + 1), type = c("perc", "bca")) with(out, c(Est = t0, pLL = percent[4], pUL = percent[5], bcaLL = bca[4], bcaLL = bca[5])) })) ## add row names row.names(parms) <- names(coef(m1)) ## print results parms
## Est pLL pUL bcaLL bcaLL ## count_(Intercept) 1.5979 0.8793 2.07810 1.087354 2.22614 ## count_child -1.0428 -1.7509 -0.17531 -1.618509 -0.02203 ## count_camper1 0.8340 0.0596 1.62653 0.001571 1.59995 ## zero_(Intercept) 1.2974 0.3503 2.21984 0.293577 2.12070 ## zero_persons -0.5643 -1.1087 -0.07847 -1.008526 0.00633
## compare with normal based approximation confint(m1)
## 2.5 % 97.5 % ## count_(Intercept) 1.4302 1.7655 ## count_child -1.2388 -0.8469 ## count_camper1 0.6505 1.0175 ## zero_(Intercept) 0.5647 2.0302 ## zero_persons -0.8838 -0.2449
The bootstrapped confidence intervals are considerably wider than the normal based approximation. The bootstrapped CIs are more consistent with the CIs from Stata when using robust standard errors.
Now we can estimate the incident risk ratio (IRR) for the Poisson model and
odds ratio (OR) for the logistic (zero inflation) model. This is done using
almost identical code as before, but passing a transformation function to the
h argument of boot.ci, in this case, exp to exponentiate.
## exponentiated parameter estimates with percentile and bias adjusted CIs expparms <- t(sapply(c(1, 3, 5, 7, 9), function(i) { out <- boot.ci(res, index = c(i, i + 1), type = c("perc", "bca"), h = exp) with(out, c(Est = t0, pLL = percent[4], pUL = percent[5], bcaLL = bca[4], bcaLL = bca[5])) })) ## add row names row.names(expparms) <- names(coef(m1)) ## print results expparms
## Est pLL pUL bcaLL bcaLL ## count_(Intercept) 4.9426 2.4091 7.9892 2.9664 9.2641 ## count_child 0.3525 0.1736 0.8392 0.1982 0.9782 ## count_camper1 2.3026 1.0614 5.0862 1.0016 4.9528 ## zero_(Intercept) 3.6599 1.4195 9.2058 1.3412 8.3370 ## zero_persons 0.5687 0.3300 0.9245 0.3648 1.0063
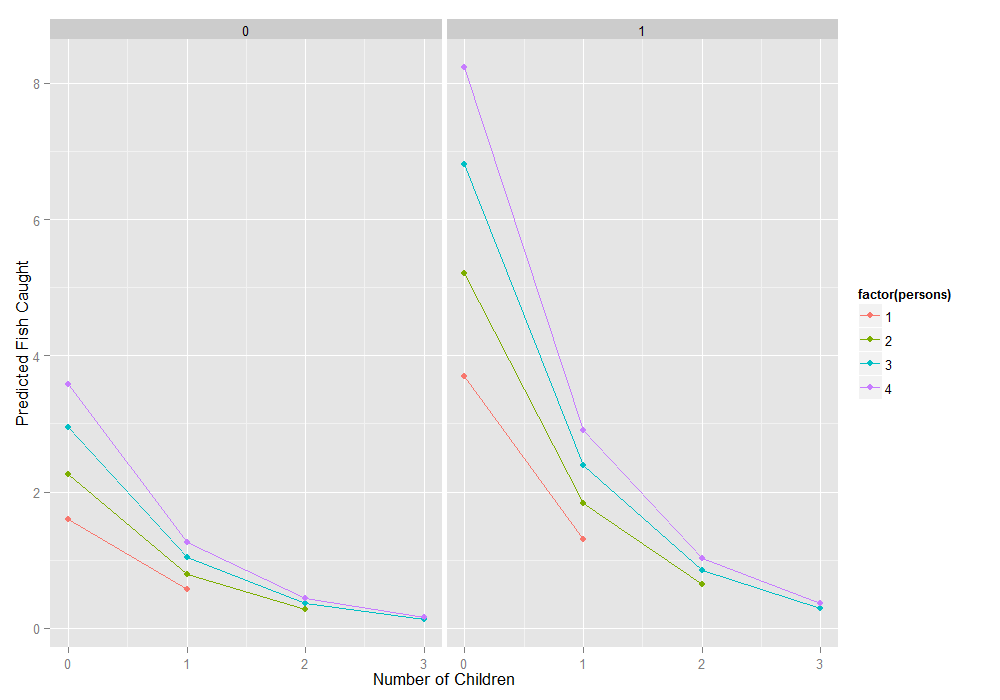
To better understand our model, we can compute the expected number of fish
caught for different combinations of our predictors. In fact, since we are
working with essentially categorical predictors, we can compute the expected
values for all combinations using the expand.grid function to create
all combinations and then the predict function to do it. We also remove any rows where the number of children exceeds the number of persons, which does not make sense logically, using the subset function. Finally we
create a graph.
newdata1 <- expand.grid(0:3, factor(0:1), 1:4) colnames(newdata1) <- c("child", "camper", "persons") newdata1 <- subset(newdata1, subset=(child<=persons)) newdata1$phat <- predict(m1, newdata1) ggplot(newdata1, aes(x = child, y = phat, colour = factor(persons))) + geom_point() + geom_line() + facet_wrap(~camper) + labs(x = "Number of Children", y = "Predicted Fish Caught")
Things to consider
- Since zip has both a count model and a logit model, each of the two models should have good predictors. The two models do not necessarily need to use the same predictors.
- Problems of perfect prediction, separation or partial separation can occur in the logistic part of the zero-inflated model.
- Count data often use exposure variables to indicate the number of times the event
could have happened. You can incorporate a logged version of the exposure variable into your model by using the
offset()option. - It is not recommended that zero-inflated Poisson models be applied to small samples. What constitutes a small sample does not seem to be clearly defined in the literature.
- Pseudo-R-squared values differ from OLS R-squareds, please see FAQ: What are pseudo R-squareds? for a discussion on this issue.
- In times past, the Vuong test had been used to test whether a zero-inflated Poisson model or a Poisson model (without the zero-inflation) was a better fit for the data. However, this test is no longer considered valid. Please see The Misuse of The Vuong Test For Non-Nested Models to Test for Zero-Inflation by Paul Wilson for further information.
See Also
zeroinfl
References
- Long, J. S. 1997. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications. Everitt, B. S. and Hothorn, T. A Handbook of Statistical Analyses Using R
