This example is taken from Levy and Lemeshow’s Sampling of Populations.
page 53 simple random sampling
A short "movie" of how to convert the SAS data set wvmomsag into a WesVar data set can be viewed by clicking here. Note that a new variable, called psu, was added to the data set while it was still in SAS. This variable is just a counting variable (i.e., an index or an identification variable) that will be used as the PSU (primary sampling unit) variable.
We have created a web page that parallels this page and gives written explanation of the point-and-click steps shown in all of the movies on this page. This page is useful if you have difficulty viewing the movies or if you want reminder notes for use at a later time. To view this page, click here.
When using a simple random sampling design, the only elements that you will need to identify to WesVar are the weight variable, the PSU variable, which WesVar calls the VarUnit, and the analysis variable. In this example, the weight variable is called weight1, the VarUnit is called psu, and the analysis variable is called hospno. We used the variable hospno to create our table because hospno has only one value; hence, it adds only one row to our table. In other examples, we often add a variable called cons that has only one value to use to make the table. We will use the jackknife1 (jk1) method because we do not have stratification in our sample design.
A second "movie" shows how to analyze the data once it is in WesVar format. You can view that movie by clicking here.
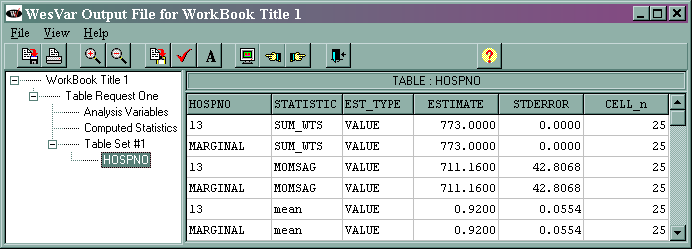
The output (shown at the end of the analysis "movie") is given below.
For most situations, only the values given on the lines that say "MARGINAL" are of interest. The other values listed in the column, called "HOSPNO" in this example, are the values of that variable. In this example, there is only one value of hospno and that is 13. If we had selected a different variable as the analysis variable, the values and the name of the column would reflect that variable. The marginal sum_wts value of 773 is the estimated population total. The marginal momsag value of 711.16 is the estimated total for the variable momsag, and its standard error is 42.8068. The marginal mean value of 0.92 is the estimated mean of the variable momsag, and its standard error is 0.0554. The column labeled CELL_n gives the number of observations in each cell.
This example is taken from Lehtonen and Pahkinen’s Practical Methods for Design and Analysis of Complex Surveys.
page 29 Table 2.4 Estimates from a simple random sample drawn without replacement (n = 8); the Province’91 population. A short "movie" showing how to convert the SAS data set page29 into a WesVar data set can by viewed by clicking here. Another "movie" showing how to analyze the data can be viewed by clicking here.
In this example, the variable wt is used as the weight variable, cluster is used as the VarUnit, and ue91 is used as the analysis variable. Because the sampling design was a simple random sample, we use the jackknife1 (jk1) method of creating the replicate weights. Also note that because the sample size is large relative to the population (eight elements sampled from a population of 32 elements), we need to use a finite population correction (FPC). To calculate the FPC, use the formula 1 – (n/N), where n is the sample size and N is the size of the population. In this case, 1 – (8/32) = .75.
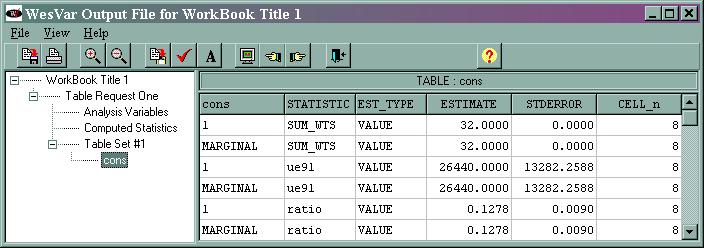
The output (shown at the end of the analysis "movie") is given below.
The marginal sum_wts value of 32 is the estimated population total. The marginal ue91 value of 26440 is the estimated total of the variable ue91, and its standard error is 13282.2588. The marginal ratio value of 0.1278 is the estimated ratio of ue91/lab91, and its standard error is 0.0090. This is slightly different from what is shown in the text, and we do not know why. The output for the median is not shown above. The median and its standard error are different from those shown in the text. We suspect that this might reflect a difference in the algorithms used by the different statistical packages.
Calculating ratios with a simple random sample
This example is taken from Levy and Lemeshow’s Sampling of Populations.
page 200 ratio estimation
A short "movie" of how to convert the SAS data set tab7pt1 into a WesVar data set can be viewed by clicking here. A second "movie" shows how to analyze the data once it is in WesVar format. You can view that movie by clicking here.
In this example, the variable wt1 is used as the weight variable, the variable area is used as the VarUnit, and the variable totmedex is used as the analysis variable. The variable totcnt is used to make the table. The variable totcnt was selected as the variable used to make the table because it only has one value; hence, it only adds one row to the table entries, making the table easier to read. The jackknife-1 (jk1) method of creating the replicate weight is used because we do not have stratification in this design.
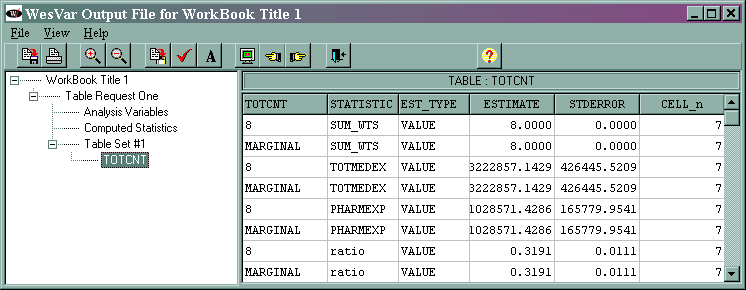
The output (shown at the end of the analysis "movie") is given below.
The marginal sum_wts value of 8 is the estimated population total. The marginal totmedex value of 3222857.1429 is the estimated total of the variable totmedex, and its standard error is 150771.2598. The marginal phramexp value of 1028571.4286 is the estimated total of pharmexp, and its standard error is 58612.0649. The marginal ratio value of 0.3191 is the estimated ratio of pharmexp/totmedex, and its standard error is 0.0039.