This example is taken from Lehtonen and Pahkinen’s Practical Methods for Design and Analysis of Complex Surveys.
page 60 Table 2.8 Estimates under a PPSSYS design (n = 8); the Province’91 population.
The SAS data file for this example can be downloaded by clicking here. Note that a modification was made to this data set: variables called id and cons were added to the data set. The variable id starts at one and counts the number of observations in each strata. This is necessary for use in WesVar as the VarUnit variable (in other words, this variable is the PSU) because the PSUs within each strata must be numbered consecutively starting with one. The variable cons was added for use in making the table. The variable cons is equal to one for all cases. Please note that there are other ways to analyze these data. Another way to analyze the data would be to copy the observation in strata 2 (the certainty or self-representing PSU), so that there were two observations in strata 2. The weight of each of these observations would be reduced from one to one-half. When analyzing the data in WesVar, you would not specify strata 2 as having a self-representing PSU.
In this example, the variable wt is used as the weight variable, the variable id is used as the VarUnit and the variable str is used as the StratVar (the variable that defines the strata). The jackknife-n (jkn) method of creating the replicate weights is used because it allows more than two PSUs per strata (as we have in strata 1). Also, we will need to use an FPC of .75 (1 – (8/32) = .75).
The output is given below.
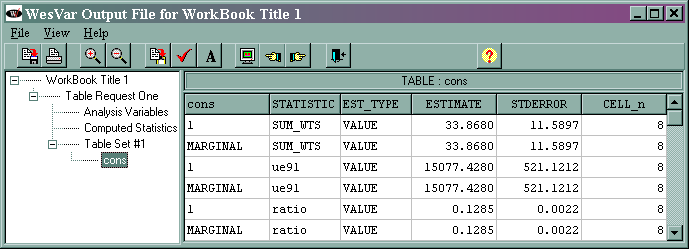
The marginal sum_wts value of 33.8680 is incorrect because of the addition of the second observation in strata two (the correct value is 32). The marginal ue91 value of 15077.4280 is the estimated total of the variable ue91, and its standard error is 521.1212. The marginal ratio value of 0.1285 is the estimated ratio of ue91/lab91, and its standard error is 0.0022. Note that the cell totals listed in the right-most column are incorrect because of the modification that was made to the data set.